Dynamical Systems in Neuroscience:
Share Embed Flag
Download ePaper

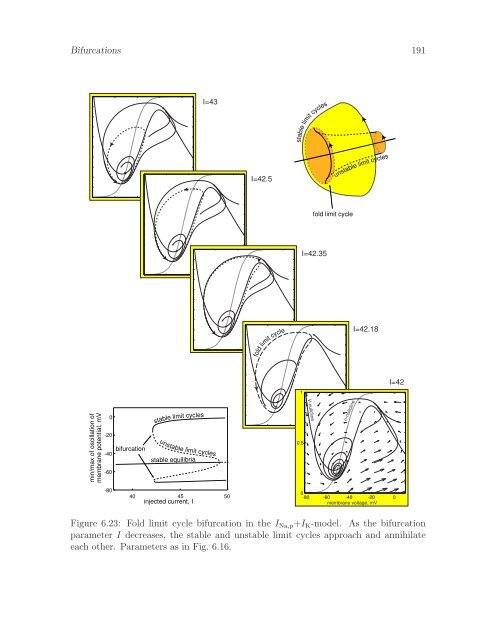
Dynamical Systems in Neuroscience:

Dynamical Systems in Neuroscience: Dynamical Systems in Neuroscience:

ib.cnea.gov.ar
from ib.cnea.gov.ar More from this publisher
12.07.2015 Views

190 Bifurcationsstableunstablelimit cyclelimitcyclefoldlimitcycleFigure 6.22: Fold limit cycle bifurcation: A stable and an unstable limit cycle approachand annihilate each other.bifurcation parameter approaches the bifurcation value I b .6.2.3 Fold limit cycleA stable limit cycle can appear (or disappear) via the fold limit cycle bifurcationdepicted in Fig. 6.22. Let us consider the figure from left to right, which corresponds tothe disappearance of the limit cycle, and hence to the disappearance of periodic spikingactivity. As the bifurcation parameter changes, the stable limit cycle is approached byan unstable one, they coalesce and annihilate each other. At the point of annihilation,there is a periodic orbit, but it is neither stable nor unstable. More precisely, it is stablefrom the side corresponding to the stable cycle (outside in Fig. 6.22), and unstable fromthe other side (inside in Fig. 6.22). This periodic orbit is referred to as being a fold(also known as a saddle-node) limit cycle, and it is analogous to the fold (saddle-node)equilibrium studied in Sect. 6.1. Considering Fig. 6.22 from right to left explains howa stable limit cycle can appear seemingly out of nowhere: As a bifurcation parameterchanges, a fold limit cycle appears, which then bifurcates into a stable limit cycle andan unstable one.Fold limit cycle bifurcation can occur in the I Na,p +I K -model having low-thresholdK + current, as we demonstrate in Fig. 6.23. The top phase portrait corresponding toI = 43 is the same as the one in Fig. 6.16. In that figure we studied how the equilibriumloses stability via subcritical Andronov-Hopf bifurcation, which occurs when anunstable limit cycle shrinks to a point. We never questioned where the unstable limitcycle came from. Neither were we concerned with the existence of a large-amplitudestable limit cycle corresponding to the periodic spiking state. In Fig. 6.23 we studythis problem. We decrease the bifurcation parameter I to see what happens with thelimit cycles. As I approaches the bifurcation value 42.18, the unstable and stable limitcycles approach and annihilate each other. When I is less than the bifurcation value,there are no periodic orbits, only one stable equilibrium corresponding to the restingstate.Notice that the fold limit cycle bifurcation explains how (un)stable limit cycles

Bifurcations 191I=43limitcyclesstableI=42.5unstable limitcyclesfold limit cycleI=42.35foldlimitcycleI=42.181I=42V-nullclinemin/max of oscillation ofmembrane potential, mV0-20-40-60bifurcationstablelimit cyclesunstable limit cyclesstable equilibria0.5n-nullcline-8040 45 50injected current, I0-80 -60 -40 -20 0membrane voltage, mVFigure 6.23: Fold limit cycle bifurcation in the I Na,p +I K -model. As the bifurcationparameter I decreases, the stable and unstable limit cycles approach and annihilateeach other. Parameters as in Fig. 6.16.

Bifurcations 191I=43limitcyclesstableI=42.5unstable limitcyclesfold limit cycleI=42.35foldlimitcycleI=42.181I=42V-nullcl<strong>in</strong>em<strong>in</strong>/max of oscillation ofmembrane potential, mV0-20-40-60bifurcationstablelimit cyclesunstable limit cyclesstable equilibria0.5n-nullcl<strong>in</strong>e-8040 45 50<strong>in</strong>jected current, I0-80 -60 -40 -20 0membrane voltage, mVFigure 6.23: Fold limit cycle bifurcation <strong>in</strong> the I Na,p +I K -model. As the bifurcationparameter I decreases, the stable and unstable limit cycles approach and annihilateeach other. Parameters as <strong>in</strong> Fig. 6.16.

logo

products

Resources

Company

Terms of service
Privacy policy
Cookie policy
Cookie settings
Imprint
Change language
Made with love in Switzerland
© 2024 Yumpu.com all rights reserved

Hooray! Your file is uploaded and ready to be published.

Saved successfully!

Ooh no, something went wrong!