REVIEW 3: Key 1. Given the iterated integral â« 3 â« 9 y sin(x 2) dx ...
REVIEW 3: Key 1. Given the iterated integral â« 3 â« 9 y sin(x 2) dx ...
REVIEW 3: Key 1. Given the iterated integral â« 3 â« 9 y sin(x 2) dx ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
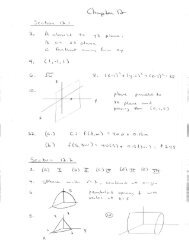
<strong>REVIEW</strong> 3: <strong>Key</strong>∫ 3 ∫ 9<strong>1.</strong> <strong>Given</strong> <strong>the</strong> <strong>iterated</strong> <strong>integral</strong> y <strong>sin</strong>(x 2 ) <strong>dx</strong> dy, draw <strong>the</strong> correspondingregion of integration on <strong>the</strong> xy-plane, reverse <strong>the</strong> order of integration, and0 y 2evaluate <strong>the</strong> <strong>integral</strong>.Solution:y ∫ 3 ∫ 930 y2.5∫ 29 ∫ √ y= x2<strong>1.</strong>510.52 4 6 8x== 1 20 y=0∫ 90y <strong>sin</strong>(x 2 ) <strong>dx</strong> dyx <strong>sin</strong>(x 2 ) <strong>dx</strong><strong>sin</strong>(x 2 ) y dy <strong>dx</strong>= − 1 4 cos(x2 )∣ 9 0= 1 4(1 − cos 81) ≈ 0.0558.2. Find <strong>the</strong> volume under <strong>the</strong> graph of <strong>the</strong> function f(x, y) = 3xy +y 2 over<strong>the</strong> region R defined by <strong>the</strong> inequalities x ⩾ 0, y ⩾ 0, and x + 2y ⩽ 2.Solution:The region of integration is <strong>the</strong> triangle bounded by lines x = 0, y = 0, an<strong>dx</strong> + 2y = 2.V ====∫ 2 ∫ y=1−x/20∫ 20∫ 20∫ 20y=0( 32 xy2 + y33 y=0( 32 x(1 − x/2)2 +(3xy + y 2 ) dy <strong>dx</strong>) y=1−x/2<strong>dx</strong>(1 −)x/2)3<strong>dx</strong>3124 (4x3 − 15x 2 + 12x + 4) <strong>dx</strong> = 2 3 .3. Find <strong>the</strong> mass of <strong>the</strong> pyramid bounded by <strong>the</strong> planes x = 0, y = 0,z = 1, and 3x + 2y + z = 7 given <strong>the</strong> mass density function δ(x, y, z) = 2z.<strong>Key</strong>:∫ 2 ∫ 3−3x/2 ∫ 7−3x−2y4. Find <strong>the</strong> double <strong>integral</strong>001∫ 3π/4 ∫ 4/ <strong>sin</strong> θπ/402z dz dy <strong>dx</strong> = 30.r dr dθ1
in polar coordinates and sketch <strong>the</strong> region of integration. Interpret <strong>the</strong> double<strong>integral</strong> geometrically as an area or volume.<strong>Key</strong>:∫ 3π/4 ∫ 4/ <strong>sin</strong> θπ/40r dr dθ =∫ 3π/4π/48<strong>sin</strong> 2 dθ = 16.θThe region is <strong>the</strong> triangle bounded by <strong>the</strong> lines y = x, y = −x, and y = 4.The double <strong>integral</strong> is <strong>the</strong> area of <strong>the</strong> region; it is also <strong>the</strong> volume of <strong>the</strong> solidbetween <strong>the</strong> planes z = 0 and z = 1 over <strong>the</strong> region.5. U<strong>sin</strong>g cylindrical coordinates, find <strong>the</strong> mass of <strong>the</strong> upper half (above<strong>the</strong> xy-plane) of <strong>the</strong> unit ball x 2 + y 2 + z 2 ⩽ 1 given <strong>the</strong> mass density functionδ(x, y, z) = z. Find <strong>the</strong> same mass u<strong>sin</strong>g spherical coordinates.<strong>Key</strong>:∫ 2π ∫ 100( ∫√ )1−r 2z dz r dr dθ = π ∫ 2π4 =00∫ π/2 ∫ 16. Find parametric equations of(a) <strong>the</strong> straight line through <strong>the</strong> points (1, 2, −1) and (2, 3, 4);<strong>Key</strong>:⎧⎪⎨ x = 1 + ty = 2 + t⎪⎩z = −1 + 5t00ρ cos φ ρ 2 <strong>sin</strong> φ dρ dφ dθ.(b) <strong>the</strong> circle of radius 4 centered at <strong>the</strong> point (−1, 3, 5) and lying in <strong>the</strong>plane parallel to <strong>the</strong> xz-plane.<strong>Key</strong>:⎧⎪⎨ x = −1 + 4 cos ty = 3⎪⎩z = 5 + 4 <strong>sin</strong> t2