v2010.10.26 - Convex Optimization
v2010.10.26 - Convex Optimization v2010.10.26 - Convex Optimization
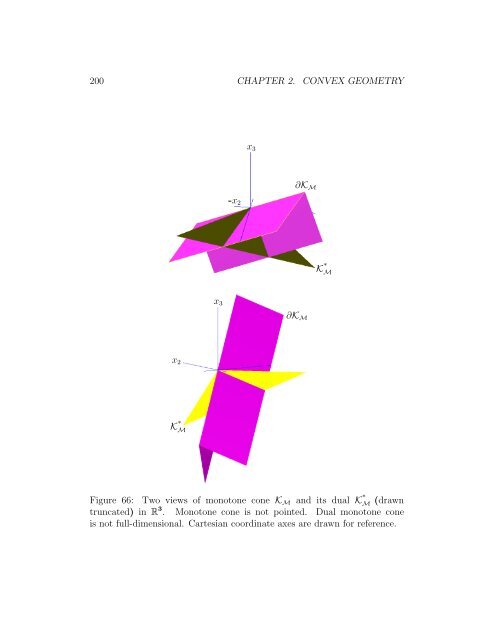
200 CHAPTER 2. CONVEX GEOMETRY-x 2x 3∂K MK ∗ Mx 2x 3∂K MK ∗ MFigure 66: Two views of monotone cone K M and its dual K ∗ M (drawntruncated) in R 3 . Monotone cone is not pointed. Dual monotone coneis not full-dimensional. Cartesian coordinate axes are drawn for reference.
2.13. DUAL CONE & GENERALIZED INEQUALITY 201where N = n −1, and because K M is closed and convex, we may adapt ConeTable 1 (p.194) as follows:Cone Table 1* K ∗ K ∗∗ = Kvertex-description X ∗ X ∗†T , ±X ∗⊥halfspace-description X ∗† , X ∗⊥T X ∗TThe vertex-description for K M is thereforewhere X ∗⊥ = 1 andK M = {[X ∗†T X ∗⊥ −X ∗⊥ ]a | a ≽ 0} ⊂ R n (439)⎡⎤n − 1 −1 −1 · · · −1 −1 −1n − 2 n − 2 −2... · · · −2 −2X ∗† = 1 . n − 3 n − 3 . .. −(n − 4) . −3n3 . n − 4 . ∈ R.. n−1×n−(n − 3) −(n − 3) .⎢⎥⎣ 2 2 · · ·... 2 −(n − 2) −(n − 2) ⎦while1 1 1 · · · 1 1 −(n − 1)(440)K ∗ M = {y ∈ R n | X ∗† y ≽ 0, X ∗⊥T y = 0} (441)is the dual monotone cone halfspace-description.2.13.9.4.4 Exercise. Inside the monotone cones.Mathematically describe the respective interior of the monotone nonnegativecone and monotone cone. In three dimensions, also describe the relativeinterior of each face.2.13.9.5 More pointed cone descriptions with equality conditionConsider pointed polyhedral cone K having a linearly independent set ofgenerators and whose subspace membership is explicit; id est, we are giventhe ordinary halfspace-descriptionK = {x | Ax ≽ 0, Cx = 0} ⊆ R n(287a)
- Page 149 and 150: 2.12. CONVEX POLYHEDRA 149convex po
- Page 151 and 152: 2.12. CONVEX POLYHEDRA 1512.12.2.2
- Page 153 and 154: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 155 and 156: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 157 and 158: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 159 and 160: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 161 and 162: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 163 and 164: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 165 and 166: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 167 and 168: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 169 and 170: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 171 and 172: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 173 and 174: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 175 and 176: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 177 and 178: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 179 and 180: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 181 and 182: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 183 and 184: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 185 and 186: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 187 and 188: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 189 and 190: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 191 and 192: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 193 and 194: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 195 and 196: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 197 and 198: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 199: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 203 and 204: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 205 and 206: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 207 and 208: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 209 and 210: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 211 and 212: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 213 and 214: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 215 and 216: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 217 and 218: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 219 and 220: Chapter 3Geometry of convex functio
- Page 221 and 222: 3.1. CONVEX FUNCTION 221f 1 (x)f 2
- Page 223 and 224: 3.1. CONVEX FUNCTION 223Rf(b)f(X
- Page 225 and 226: 3.2. PRACTICAL NORM FUNCTIONS, ABSO
- Page 227 and 228: 3.2. PRACTICAL NORM FUNCTIONS, ABSO
- Page 229 and 230: 3.2. PRACTICAL NORM FUNCTIONS, ABSO
- Page 231 and 232: 3.2. PRACTICAL NORM FUNCTIONS, ABSO
- Page 233 and 234: 3.2. PRACTICAL NORM FUNCTIONS, ABSO
- Page 235 and 236: 3.3. INVERTED FUNCTIONS AND ROOTS 2
- Page 237 and 238: 3.4. AFFINE FUNCTION 237rather]x >
- Page 239 and 240: 3.4. AFFINE FUNCTION 239f(z)Az 2z 1
- Page 241 and 242: 3.5. EPIGRAPH, SUBLEVEL SET 241{a T
- Page 243 and 244: 3.5. EPIGRAPH, SUBLEVEL SET 243Subl
- Page 245 and 246: 3.5. EPIGRAPH, SUBLEVEL SET 245wher
- Page 247 and 248: 3.5. EPIGRAPH, SUBLEVEL SET 247part
- Page 249 and 250: 3.5. EPIGRAPH, SUBLEVEL SET 249that
200 CHAPTER 2. CONVEX GEOMETRY-x 2x 3∂K MK ∗ Mx 2x 3∂K MK ∗ MFigure 66: Two views of monotone cone K M and its dual K ∗ M (drawntruncated) in R 3 . Monotone cone is not pointed. Dual monotone coneis not full-dimensional. Cartesian coordinate axes are drawn for reference.