- Page 1 and 2:
DATTORROCONVEXOPTIMIZATION&EUCLIDEA
- Page 3 and 4:
Convex Optimization&Euclidean Dista
- Page 5 and 6:
for Jennie Columba♦Antonio♦♦&
- Page 7 and 8:
PreludeThe constant demands of my d
- Page 9 and 10:
Convex Optimization&Euclidean Dista
- Page 11 and 12:
CONVEX OPTIMIZATION & EUCLIDEAN DIS
- Page 13 and 14:
List of Figures1 Overview 211 Orion
- Page 15 and 16:
LIST OF FIGURES 1562 Shrouded polyh
- Page 17:
LIST OF FIGURES 17130 Elliptope E 3
- Page 21 and 22:
Chapter 1OverviewConvex Optimizatio
- Page 23 and 24:
ˇx 4ˇx 3ˇx 2Figure 2: Applicatio
- Page 25 and 26:
25Figure 4: This coarsely discretiz
- Page 27 and 28:
(biorthogonal expansion) is examine
- Page 29 and 30:
29cardinality Boolean solution to a
- Page 31 and 32:
31Figure 8: Robotic vehicles in con
- Page 33 and 34:
an elaborate exposition offering in
- Page 35 and 36:
Chapter 2Convex geometryConvexity h
- Page 37 and 38:
2.1. CONVEX SET 372.1.2 linear inde
- Page 39 and 40:
2.1. CONVEX SET 392.1.6 empty set v
- Page 41 and 42:
2.1. CONVEX SET 41(a)R(b)R 2(c)R 3F
- Page 43 and 44:
2.1. CONVEX SET 43where Q∈ R 3×3
- Page 45 and 46:
2.1. CONVEX SET 45Now let’s move
- Page 47 and 48:
2.1. CONVEX SET 47By additive inver
- Page 49 and 50:
2.1. CONVEX SET 49R nR mR(A T )x px
- Page 51 and 52:
2.2. VECTORIZED-MATRIX INNER PRODUC
- Page 53 and 54:
2.2. VECTORIZED-MATRIX INNER PRODUC
- Page 55 and 56:
2.2. VECTORIZED-MATRIX INNER PRODUC
- Page 57 and 58:
2.2. VECTORIZED-MATRIX INNER PRODUC
- Page 59 and 60:
2.2. VECTORIZED-MATRIX INNER PRODUC
- Page 61 and 62:
2.3. HULLS 61Figure 20: Convex hull
- Page 63 and 64:
2.3. HULLS 63Aaffine hull (drawn tr
- Page 65 and 66:
2.3. HULLS 65subset of the affine h
- Page 67 and 68:
2.3. HULLS 672.3.2.0.2 Example. Nuc
- Page 69 and 70:
2.3. HULLS 692.3.2.0.3 Exercise. Co
- Page 71 and 72:
2.3. HULLS 71Figure 24: A simplicia
- Page 73 and 74:
2.4. HALFSPACE, HYPERPLANE 73H + =
- Page 75 and 76:
2.4. HALFSPACE, HYPERPLANE 7511−1
- Page 77 and 78:
2.4. HALFSPACE, HYPERPLANE 772.4.2.
- Page 79 and 80:
2.4. HALFSPACE, HYPERPLANE 792.4.2.
- Page 81 and 82:
2.4. HALFSPACE, HYPERPLANE 81tradit
- Page 83 and 84:
2.4. HALFSPACE, HYPERPLANE 832.4.2.
- Page 85 and 86:
2.5. SUBSPACE REPRESENTATIONS 852.5
- Page 87 and 88:
2.5. SUBSPACE REPRESENTATIONS 87(Ex
- Page 89 and 90:
2.5. SUBSPACE REPRESENTATIONS 89(a)
- Page 91 and 92:
2.5. SUBSPACE REPRESENTATIONS 91are
- Page 93 and 94:
2.6. EXTREME, EXPOSED 93A one-dimen
- Page 95 and 96:
2.6. EXTREME, EXPOSED 952.6.1.1 Den
- Page 97 and 98:
2.7. CONES 97X(a)00(b)XFigure 33: (
- Page 99 and 100:
2.7. CONES 99XXFigure 37: Truncated
- Page 101 and 102:
2.7. CONES 101Figure 39: Not a cone
- Page 103 and 104:
2.7. CONES 103cone that is a halfli
- Page 105 and 106:
2.7. CONES 105A pointed closed conv
- Page 107 and 108:
2.8. CONE BOUNDARY 107That means th
- Page 109 and 110:
2.8. CONE BOUNDARY 1092.8.1.1 extre
- Page 111 and 112:
2.8. CONE BOUNDARY 1112.8.2 Exposed
- Page 113 and 114:
2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 115 and 116:
2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 117 and 118:
2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 119 and 120:
2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 121 and 122:
2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 123 and 124:
2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 125 and 126: 2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 127 and 128: 2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 129 and 130: 2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 131 and 132: 2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 133 and 134: 2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 135 and 136: 2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 137 and 138: 2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 139 and 140: 2.9. POSITIVE SEMIDEFINITE (PSD) CO
- Page 141 and 142: 2.10. CONIC INDEPENDENCE (C.I.) 141
- Page 143 and 144: 2.10. CONIC INDEPENDENCE (C.I.) 143
- Page 145 and 146: 2.10. CONIC INDEPENDENCE (C.I.) 145
- Page 147 and 148: 2.12. CONVEX POLYHEDRA 147all dimen
- Page 149 and 150: 2.12. CONVEX POLYHEDRA 149convex po
- Page 151 and 152: 2.12. CONVEX POLYHEDRA 1512.12.2.2
- Page 153 and 154: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 155 and 156: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 157 and 158: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 159 and 160: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 161 and 162: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 163 and 164: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 165 and 166: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 167 and 168: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 169 and 170: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 171 and 172: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 173 and 174: 2.13. DUAL CONE & GENERALIZED INEQU
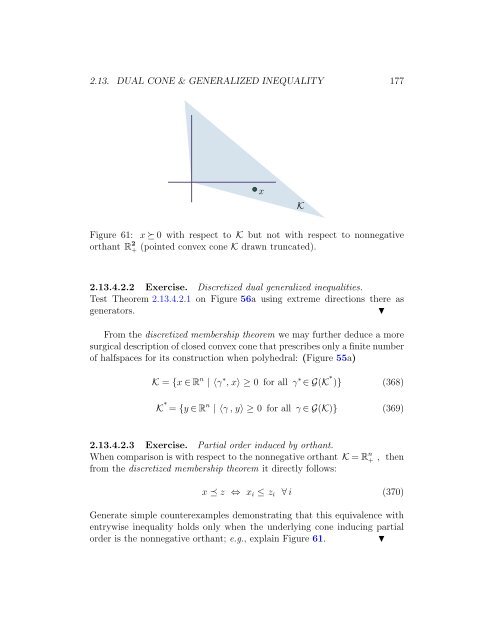
- Page 175: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 179 and 180: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 181 and 182: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 183 and 184: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 185 and 186: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 187 and 188: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 189 and 190: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 191 and 192: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 193 and 194: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 195 and 196: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 197 and 198: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 199 and 200: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 201 and 202: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 203 and 204: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 205 and 206: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 207 and 208: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 209 and 210: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 211 and 212: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 213 and 214: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 215 and 216: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 217 and 218: 2.13. DUAL CONE & GENERALIZED INEQU
- Page 219 and 220: Chapter 3Geometry of convex functio
- Page 221 and 222: 3.1. CONVEX FUNCTION 221f 1 (x)f 2
- Page 223 and 224: 3.1. CONVEX FUNCTION 223Rf(b)f(X
- Page 225 and 226: 3.2. PRACTICAL NORM FUNCTIONS, ABSO
- Page 227 and 228:
3.2. PRACTICAL NORM FUNCTIONS, ABSO
- Page 229 and 230:
3.2. PRACTICAL NORM FUNCTIONS, ABSO
- Page 231 and 232:
3.2. PRACTICAL NORM FUNCTIONS, ABSO
- Page 233 and 234:
3.2. PRACTICAL NORM FUNCTIONS, ABSO
- Page 235 and 236:
3.3. INVERTED FUNCTIONS AND ROOTS 2
- Page 237 and 238:
3.4. AFFINE FUNCTION 237rather]x >
- Page 239 and 240:
3.4. AFFINE FUNCTION 239f(z)Az 2z 1
- Page 241 and 242:
3.5. EPIGRAPH, SUBLEVEL SET 241{a T
- Page 243 and 244:
3.5. EPIGRAPH, SUBLEVEL SET 243Subl
- Page 245 and 246:
3.5. EPIGRAPH, SUBLEVEL SET 245wher
- Page 247 and 248:
3.5. EPIGRAPH, SUBLEVEL SET 247part
- Page 249 and 250:
3.5. EPIGRAPH, SUBLEVEL SET 249that
- Page 251 and 252:
3.6. GRADIENT 251respect to its vec
- Page 253 and 254:
3.6. GRADIENT 253Invertibility is g
- Page 255 and 256:
3.6. GRADIENT 2553.6.1.0.2 Theorem.
- Page 257 and 258:
3.6. GRADIENT 257f(Y )[ ∇f(X)−1
- Page 259 and 260:
3.6. GRADIENT 259αβα ≥ β ≥
- Page 261 and 262:
3.6. GRADIENT 2613.6.4 second-order
- Page 263 and 264:
3.7. CONVEX MATRIX-VALUED FUNCTION
- Page 265 and 266:
3.7. CONVEX MATRIX-VALUED FUNCTION
- Page 267 and 268:
3.7. CONVEX MATRIX-VALUED FUNCTION
- Page 269 and 270:
3.8. QUASICONVEX 269exponential alw
- Page 271 and 272:
3.9. SALIENT PROPERTIES 2713.8.0.0.
- Page 273 and 274:
Chapter 4Semidefinite programmingPr
- Page 275 and 276:
4.1. CONIC PROBLEM 275(confer p.162
- Page 277 and 278:
4.1. CONIC PROBLEM 277PCsemidefinit
- Page 279 and 280:
4.1. CONIC PROBLEM 279is the affine
- Page 281 and 282:
4.1. CONIC PROBLEM 281faces of S 3
- Page 283 and 284:
4.1. CONIC PROBLEM 2834.1.2.3 Previ
- Page 285 and 286:
4.2. FRAMEWORK 285Semidefinite Fark
- Page 287 and 288:
4.2. FRAMEWORK 287On the other hand
- Page 289 and 290:
4.2. FRAMEWORK 2894.2.2.1 Dual prob
- Page 291 and 292:
4.2. FRAMEWORK 291For symmetric pos
- Page 293 and 294:
4.2. FRAMEWORK 293has norm ‖x ⋆
- Page 295 and 296:
4.2. FRAMEWORK 295minimize 1 TˆxX
- Page 297 and 298:
4.2. FRAMEWORK 297asminimize ‖ỹ
- Page 299 and 300:
4.3. RANK REDUCTION 2994.3 Rank red
- Page 301 and 302:
4.3. RANK REDUCTION 301A rank-reduc
- Page 303 and 304:
4.3. RANK REDUCTION 303(t ⋆ i)
- Page 305 and 306:
4.3. RANK REDUCTION 3054.3.3.0.1 Ex
- Page 307 and 308:
4.3. RANK REDUCTION 3074.3.3.0.2 Ex
- Page 309 and 310:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 311 and 312:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 313 and 314:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 315 and 316:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 317 and 318:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 319 and 320:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 321 and 322:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 323 and 324:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 325 and 326:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 327 and 328:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 329 and 330:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 331 and 332:
4.4. RANK-CONSTRAINED SEMIDEFINITE
- Page 333 and 334:
4.5. CONSTRAINING CARDINALITY 333mi
- Page 335 and 336:
4.5. CONSTRAINING CARDINALITY 3350R
- Page 337 and 338:
4.5. CONSTRAINING CARDINALITY 337it
- Page 339 and 340:
4.5. CONSTRAINING CARDINALITY 339m/
- Page 341 and 342:
4.5. CONSTRAINING CARDINALITY 341we
- Page 343 and 344:
4.5. CONSTRAINING CARDINALITY 343fl
- Page 345 and 346:
4.5. CONSTRAINING CARDINALITY 345We
- Page 347 and 348:
4.5. CONSTRAINING CARDINALITY 3474.
- Page 349 and 350:
4.5. CONSTRAINING CARDINALITY 349R
- Page 351 and 352:
4.5. CONSTRAINING CARDINALITY 351pe
- Page 353 and 354:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 355 and 356:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 357 and 358:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 359 and 360:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 361 and 362:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 363 and 364:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 365 and 366:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 367 and 368:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 369 and 370:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 371 and 372:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 373 and 374:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 375 and 376:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 377 and 378:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 379 and 380:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 381 and 382:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 383 and 384:
4.6. CARDINALITY AND RANK CONSTRAIN
- Page 385 and 386:
4.7. CONSTRAINING RANK OF INDEFINIT
- Page 387 and 388:
4.7. CONSTRAINING RANK OF INDEFINIT
- Page 389 and 390:
4.7. CONSTRAINING RANK OF INDEFINIT
- Page 391 and 392:
4.8. CONVEX ITERATION RANK-1 391whi
- Page 393 and 394:
4.8. CONVEX ITERATION RANK-1 393the
- Page 395 and 396:
Chapter 5Euclidean Distance MatrixT
- Page 397 and 398:
5.2. FIRST METRIC PROPERTIES 397to
- Page 399 and 400:
5.3. ∃ FIFTH EUCLIDEAN METRIC PRO
- Page 401 and 402:
5.3. ∃ FIFTH EUCLIDEAN METRIC PRO
- Page 403 and 404:
5.4. EDM DEFINITION 403The collecti
- Page 405 and 406:
5.4. EDM DEFINITION 4055.4.2 Gram-f
- Page 407 and 408:
5.4. EDM DEFINITION 407We provide a
- Page 409 and 410:
5.4. EDM DEFINITION 4095.4.2.3.1 Ex
- Page 411 and 412:
5.4. EDM DEFINITION 411is the fact:
- Page 413 and 414:
5.4. EDM DEFINITION 413Figure 120:
- Page 415 and 416:
5.4. EDM DEFINITION 415is found fro
- Page 417 and 418:
5.4. EDM DEFINITION 417one less dim
- Page 419 and 420:
5.4. EDM DEFINITION 419equality con
- Page 421 and 422:
5.4. EDM DEFINITION 421How much dis
- Page 423 and 424:
5.4. EDM DEFINITION 423105ˇx 4ˇx
- Page 425 and 426:
5.4. EDM DEFINITION 425now implicit
- Page 427 and 428:
5.4. EDM DEFINITION 427by translate
- Page 429 and 430:
5.4. EDM DEFINITION 429Crippen & Ha
- Page 431 and 432:
5.4. EDM DEFINITION 431where ([√t
- Page 433 and 434:
5.4. EDM DEFINITION 433because (A.3
- Page 435 and 436:
5.5. INVARIANCE 4355.5.1.0.1 Exampl
- Page 437 and 438:
5.5. INVARIANCE 437x 2 x 2x 3 x 1 x
- Page 439 and 440:
5.6. INJECTIVITY OF D & UNIQUE RECO
- Page 441 and 442:
5.6. INJECTIVITY OF D & UNIQUE RECO
- Page 443 and 444:
5.6. INJECTIVITY OF D & UNIQUE RECO
- Page 445 and 446:
5.7. EMBEDDING IN AFFINE HULL 4455.
- Page 447 and 448:
5.7. EMBEDDING IN AFFINE HULL 447Fo
- Page 449 and 450:
5.7. EMBEDDING IN AFFINE HULL 4495.
- Page 451 and 452:
5.8. EUCLIDEAN METRIC VERSUS MATRIX
- Page 453 and 454:
5.8. EUCLIDEAN METRIC VERSUS MATRIX
- Page 455 and 456:
5.8. EUCLIDEAN METRIC VERSUS MATRIX
- Page 457 and 458:
5.8. EUCLIDEAN METRIC VERSUS MATRIX
- Page 459 and 460:
5.9. BRIDGE: CONVEX POLYHEDRA TO ED
- Page 461 and 462:
5.9. BRIDGE: CONVEX POLYHEDRA TO ED
- Page 463 and 464:
5.9. BRIDGE: CONVEX POLYHEDRA TO ED
- Page 465 and 466:
5.10. EDM-ENTRY COMPOSITION 465of a
- Page 467 and 468:
5.10. EDM-ENTRY COMPOSITION 467Then
- Page 469 and 470:
5.11. EDM INDEFINITENESS 4695.11.1
- Page 471 and 472:
5.11. EDM INDEFINITENESS 471we have
- Page 473 and 474:
5.11. EDM INDEFINITENESS 473So beca
- Page 475 and 476:
5.11. EDM INDEFINITENESS 475holds o
- Page 477 and 478:
5.12. LIST RECONSTRUCTION 477where
- Page 479 and 480:
5.12. LIST RECONSTRUCTION 479(a)(c)
- Page 481 and 482:
5.13. RECONSTRUCTION EXAMPLES 481Wi
- Page 483 and 484:
5.13. RECONSTRUCTION EXAMPLES 483d
- Page 485 and 486:
5.13. RECONSTRUCTION EXAMPLES 485Th
- Page 487 and 488:
5.14. FIFTH PROPERTY OF EUCLIDEAN M
- Page 489 and 490:
5.14. FIFTH PROPERTY OF EUCLIDEAN M
- Page 491 and 492:
5.14. FIFTH PROPERTY OF EUCLIDEAN M
- Page 493 and 494:
5.14. FIFTH PROPERTY OF EUCLIDEAN M
- Page 495 and 496:
5.14. FIFTH PROPERTY OF EUCLIDEAN M
- Page 497 and 498:
Chapter 6Cone of distance matricesF
- Page 499 and 500:
6.1. DEFINING EDM CONE 4996.1 Defin
- Page 501 and 502:
6.2. POLYHEDRAL BOUNDS 501This cone
- Page 503 and 504:
6.4. EDM DEFINITION IN 11 T 503That
- Page 505 and 506:
6.4. EDM DEFINITION IN 11 T 505N(1
- Page 507 and 508:
6.4. EDM DEFINITION IN 11 T 507Then
- Page 509 and 510:
6.4. EDM DEFINITION IN 11 T 5096.4.
- Page 511 and 512:
6.5. CORRESPONDENCE TO PSD CONE S N
- Page 513 and 514:
6.5. CORRESPONDENCE TO PSD CONE S N
- Page 515 and 516:
6.5. CORRESPONDENCE TO PSD CONE S N
- Page 517 and 518:
6.6. VECTORIZATION & PROJECTION INT
- Page 519 and 520:
6.6. VECTORIZATION & PROJECTION INT
- Page 521 and 522:
6.6. VECTORIZATION & PROJECTION INT
- Page 523 and 524:
6.7. A GEOMETRY OF COMPLETION 523(b
- Page 525 and 526:
6.7. A GEOMETRY OF COMPLETION 525[3
- Page 527 and 528:
6.7. A GEOMETRY OF COMPLETION 527wh
- Page 529 and 530:
6.8. DUAL EDM CONE 529to the geomet
- Page 531 and 532:
6.8. DUAL EDM CONE 531Proof. First,
- Page 533 and 534:
6.8. DUAL EDM CONE 533EDM 2 = S 2 h
- Page 535 and 536:
6.8. DUAL EDM CONE 535therefore the
- Page 537 and 538:
6.8. DUAL EDM CONE 537Elegance of t
- Page 539 and 540:
6.8. DUAL EDM CONE 5396.8.1.5 Affin
- Page 541 and 542:
6.8. DUAL EDM CONE 5416.8.1.7 Schoe
- Page 543 and 544:
6.8. DUAL EDM CONE 5430dvec rel ∂
- Page 545 and 546:
6.10. POSTSCRIPT 5456.10 Postscript
- Page 547 and 548:
Chapter 7Proximity problemsIn the
- Page 549 and 550:
549project on the subspace, then pr
- Page 551 and 552:
551HS N h0EDM NK = S N h ∩ R N×N
- Page 553 and 554:
5537.0.3 Problem approachProblems t
- Page 555 and 556:
7.1. FIRST PREVALENT PROBLEM: 555fi
- Page 557 and 558:
7.1. FIRST PREVALENT PROBLEM: 5577.
- Page 559 and 560:
7.1. FIRST PREVALENT PROBLEM: 559di
- Page 561 and 562:
7.1. FIRST PREVALENT PROBLEM: 5617.
- Page 563 and 564:
7.1. FIRST PREVALENT PROBLEM: 563wh
- Page 565 and 566:
7.1. FIRST PREVALENT PROBLEM: 565Th
- Page 567 and 568:
7.2. SECOND PREVALENT PROBLEM: 567O
- Page 569 and 570:
7.2. SECOND PREVALENT PROBLEM: 569S
- Page 571 and 572:
7.2. SECOND PREVALENT PROBLEM: 571r
- Page 573 and 574:
7.2. SECOND PREVALENT PROBLEM: 573w
- Page 575 and 576:
7.2. SECOND PREVALENT PROBLEM: 5757
- Page 577 and 578:
7.2. SECOND PREVALENT PROBLEM: 577a
- Page 579 and 580:
7.3. THIRD PREVALENT PROBLEM: 579is
- Page 581 and 582:
7.3. THIRD PREVALENT PROBLEM: 581We
- Page 583 and 584:
7.3. THIRD PREVALENT PROBLEM: 583su
- Page 585 and 586:
7.3. THIRD PREVALENT PROBLEM: 585Gi
- Page 587 and 588:
7.3. THIRD PREVALENT PROBLEM: 587Op
- Page 589 and 590:
7.4. CONCLUSION 589filtering, multi
- Page 591 and 592:
Appendix ALinear algebraA.1 Main-di
- Page 593 and 594:
A.1. MAIN-DIAGONAL δ OPERATOR, λ
- Page 595 and 596:
A.1. MAIN-DIAGONAL δ OPERATOR, λ
- Page 597 and 598:
A.2. SEMIDEFINITENESS: DOMAIN OF TE
- Page 599 and 600:
A.3. PROPER STATEMENTS 599(AB) T
- Page 601 and 602:
A.3. PROPER STATEMENTS 601A.3.1Semi
- Page 603 and 604:
A.3. PROPER STATEMENTS 603For A dia
- Page 605 and 606:
A.3. PROPER STATEMENTS 605Diagonali
- Page 607 and 608:
A.3. PROPER STATEMENTS 607For A,B
- Page 609 and 610:
A.3. PROPER STATEMENTS 609When B is
- Page 611 and 612:
A.4. SCHUR COMPLEMENT 611A.4 Schur
- Page 613 and 614:
A.4. SCHUR COMPLEMENT 613A.4.0.0.3
- Page 615 and 616:
A.4. SCHUR COMPLEMENT 615From Corol
- Page 617 and 618:
A.5. EIGENVALUE DECOMPOSITION 617wh
- Page 619 and 620:
A.5. EIGENVALUE DECOMPOSITION 619A.
- Page 621 and 622:
A.6. SINGULAR VALUE DECOMPOSITION,
- Page 623 and 624:
A.6. SINGULAR VALUE DECOMPOSITION,
- Page 625 and 626:
A.7. ZEROS 625A.6.5SVD of symmetric
- Page 627 and 628:
A.7. ZEROS 627(Transpose.)Likewise,
- Page 629 and 630:
A.7. ZEROS 629For X,A∈ S M +[34,2
- Page 631 and 632:
A.7. ZEROS 631A.7.5.0.1 Proposition
- Page 633 and 634:
Appendix BSimple matricesMathematic
- Page 635 and 636:
B.1. RANK-ONE MATRIX (DYAD) 635R(v)
- Page 637 and 638:
B.1. RANK-ONE MATRIX (DYAD) 637B.1.
- Page 639 and 640:
B.2. DOUBLET 639R([u v ])R(Π)= R([
- Page 641 and 642:
B.3. ELEMENTARY MATRIX 641has N −
- Page 643 and 644:
B.4. AUXILIARY V -MATRICES 643is an
- Page 645 and 646:
B.4. AUXILIARY V -MATRICES 64514. [
- Page 647 and 648:
B.5. ORTHOGONAL MATRIX 647Given X
- Page 649 and 650:
B.5. ORTHOGONAL MATRIX 649Figure 15
- Page 651 and 652:
B.5. ORTHOGONAL MATRIX 651which is
- Page 653 and 654:
Appendix CSome analytical optimal r
- Page 655 and 656:
C.2. TRACE, SINGULAR AND EIGEN VALU
- Page 657 and 658:
C.2. TRACE, SINGULAR AND EIGEN VALU
- Page 659 and 660:
C.2. TRACE, SINGULAR AND EIGEN VALU
- Page 661 and 662:
C.3. ORTHOGONAL PROCRUSTES PROBLEM
- Page 663 and 664:
C.4. TWO-SIDED ORTHOGONAL PROCRUSTE
- Page 665 and 666:
C.4. TWO-SIDED ORTHOGONAL PROCRUSTE
- Page 667 and 668:
C.4. TWO-SIDED ORTHOGONAL PROCRUSTE
- Page 669 and 670:
Appendix DMatrix calculusFrom too m
- Page 671 and 672:
D.1. DIRECTIONAL DERIVATIVE, TAYLOR
- Page 673 and 674:
D.1. DIRECTIONAL DERIVATIVE, TAYLOR
- Page 675 and 676:
D.1. DIRECTIONAL DERIVATIVE, TAYLOR
- Page 677 and 678:
D.1. DIRECTIONAL DERIVATIVE, TAYLOR
- Page 679 and 680:
D.1. DIRECTIONAL DERIVATIVE, TAYLOR
- Page 681 and 682:
D.1. DIRECTIONAL DERIVATIVE, TAYLOR
- Page 683 and 684:
D.1. DIRECTIONAL DERIVATIVE, TAYLOR
- Page 685 and 686:
D.1. DIRECTIONAL DERIVATIVE, TAYLOR
- Page 687 and 688:
D.1. DIRECTIONAL DERIVATIVE, TAYLOR
- Page 689 and 690:
D.1. DIRECTIONAL DERIVATIVE, TAYLOR
- Page 691 and 692:
D.2. TABLES OF GRADIENTS AND DERIVA
- Page 693 and 694:
D.2. TABLES OF GRADIENTS AND DERIVA
- Page 695 and 696:
D.2. TABLES OF GRADIENTS AND DERIVA
- Page 697 and 698:
D.2. TABLES OF GRADIENTS AND DERIVA
- Page 699 and 700:
Appendix EProjectionFor any A∈ R
- Page 701 and 702:
701U T = U † for orthonormal (inc
- Page 703 and 704:
E.1. IDEMPOTENT MATRICES 703where A
- Page 705 and 706:
E.1. IDEMPOTENT MATRICES 705order,
- Page 707 and 708:
E.1. IDEMPOTENT MATRICES 707are lin
- Page 709 and 710:
E.3. SYMMETRIC IDEMPOTENT MATRICES
- Page 711 and 712:
E.3. SYMMETRIC IDEMPOTENT MATRICES
- Page 713 and 714:
E.3. SYMMETRIC IDEMPOTENT MATRICES
- Page 715 and 716:
E.4. ALGEBRA OF PROJECTION ON AFFIN
- Page 717 and 718:
E.5. PROJECTION EXAMPLES 717a ∗ 2
- Page 719 and 720:
E.5. PROJECTION EXAMPLES 719where Y
- Page 721 and 722:
E.5. PROJECTION EXAMPLES 721(B.4.2)
- Page 723 and 724:
E.6. VECTORIZATION INTERPRETATION,
- Page 725 and 726:
E.6. VECTORIZATION INTERPRETATION,
- Page 727 and 728:
E.6. VECTORIZATION INTERPRETATION,
- Page 729 and 730:
E.7. PROJECTION ON MATRIX SUBSPACES
- Page 731 and 732:
E.7. PROJECTION ON MATRIX SUBSPACES
- Page 733 and 734:
E.8. RANGE/ROWSPACE INTERPRETATION
- Page 735 and 736:
E.9. PROJECTION ON CONVEX SET 735As
- Page 737 and 738:
E.9. PROJECTION ON CONVEX SET 737Wi
- Page 739 and 740:
E.9. PROJECTION ON CONVEX SET 739R(
- Page 741 and 742:
E.9. PROJECTION ON CONVEX SET 741E.
- Page 743 and 744:
E.9. PROJECTION ON CONVEX SET 743E.
- Page 745 and 746:
E.9. PROJECTION ON CONVEX SET 745Un
- Page 747 and 748:
E.9. PROJECTION ON CONVEX SET 747ac
- Page 749 and 750:
E.10. ALTERNATING PROJECTION 749bC
- Page 751 and 752:
E.10. ALTERNATING PROJECTION 7510
- Page 753 and 754:
E.10. ALTERNATING PROJECTION 753E.1
- Page 755 and 756:
E.10. ALTERNATING PROJECTION 755y 2
- Page 757 and 758:
E.10. ALTERNATING PROJECTION 757Def
- Page 759 and 760:
E.10. ALTERNATING PROJECTION 759Dis
- Page 761 and 762:
E.10. ALTERNATING PROJECTION 761mat
- Page 763 and 764:
E.10. ALTERNATING PROJECTION 763K
- Page 765 and 766:
E.10. ALTERNATING PROJECTION 765E.1
- Page 767 and 768:
E.10. ALTERNATING PROJECTION 767E.1
- Page 769 and 770:
Appendix FNotation and a few defini
- Page 771 and 772:
771A ij or A(i, j) , ij th entry of
- Page 773 and 774:
773⊞orthogonal vector sum of sets
- Page 775 and 776:
775x +vector x whose negative entri
- Page 777 and 778:
777X point list ((76) having cardin
- Page 779 and 780:
779SDPSVDSNRdBEDMS n 1S n hS n⊥hS
- Page 781 and 782:
781vectorentrycubixquartixfeasible
- Page 783 and 784:
783Oorder of magnitude information
- Page 785 and 786:
785cofmatrix of cofactors correspon
- Page 787 and 788:
Bibliography[1] Edwin A. Abbott. Fl
- Page 789 and 790:
BIBLIOGRAPHY 789[23] Dror Baron, Mi
- Page 791 and 792:
BIBLIOGRAPHY 791[49] Leonard M. Blu
- Page 793 and 794:
BIBLIOGRAPHY 793[74] Yves Chabrilla
- Page 795 and 796:
BIBLIOGRAPHY 795[102] Etienne de Kl
- Page 797 and 798:
BIBLIOGRAPHY 797[129] Carl Eckart a
- Page 799 and 800:
BIBLIOGRAPHY 799[154] James Gleik.
- Page 801 and 802:
BIBLIOGRAPHY 801[182] Johan Håstad
- Page 803 and 804:
BIBLIOGRAPHY 803[212] Viren Jain an
- Page 805 and 806:
BIBLIOGRAPHY 805[237] Monique Laure
- Page 807 and 808:
BIBLIOGRAPHY 807[265] Sunderarajan
- Page 809 and 810:
BIBLIOGRAPHY 809Notes in Computer S
- Page 811 and 812:
BIBLIOGRAPHY 811[319] Anthony Man-C
- Page 813 and 814:
BIBLIOGRAPHY 813[346] Pham Dinh Tao
- Page 815 and 816:
BIBLIOGRAPHY 815[375] Bernard Widro
- Page 817 and 818:
Index∅, see empty set0-norm, 229,
- Page 819 and 820:
INDEX 819bees, 30, 413Bellman, 276b
- Page 821 and 822:
INDEX 821circular, 130construction,
- Page 823 and 824:
INDEX 823measure, 295convex, 21, 36
- Page 825 and 826:
INDEX 825duality, 160, 410gap, 161,
- Page 827 and 828:
INDEX 827positive semidefinite, 284
- Page 829 and 830:
INDEX 829point, 39, 62positive semi
- Page 831 and 832:
INDEX 831isomorphic, 52, 56, 59, 77
- Page 833 and 834:
INDEX 833nonsymmetric, 703range, 70
- Page 835 and 836:
INDEX 835Muller, 624multidimensiona
- Page 837 and 838:
INDEX 837projection on, 739, 745tra
- Page 839 and 840:
INDEX 839pseudoinverse, 701trace, 5
- Page 841 and 842:
INDEX 841coordinate system, 156line
- Page 843 and 844:
INDEX 843nonconvex, 40, 97-101nulls
- Page 845 and 846:
INDEX 845faces, 106intersection, 10
- Page 847 and 848:
INDEX 847projection, 517symmetric,
- Page 849 and 850:
849
- Page 852:
Convex Optimization & Euclidean Dis