Force and Free Body Diagram Practice Questions - The Burns Home ...

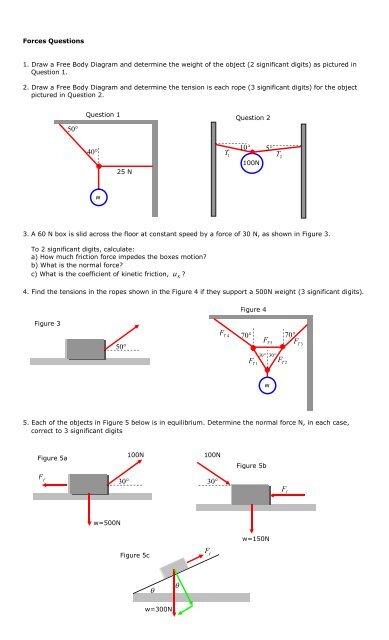
Forces Questions1. Draw a Free Body Diagram and determine the weight of the object (2 significant digits) as pictured inQuestion 1.2. Draw a Free Body Diagram and determine the tension is each rope (3 significant digits) for the objectpictured in Question 2.50Question 1Question 24025 NT 110100N5T 2w3. A 60 N box is slid across the floor at constant speed by a force of 30 N, as shown in Figure 3.To 2 significant digits, calculate:a) How much friction force impedes the boxes motion?b) What is the normal force?c) What is the coefficient of kinetic friction, K?4. Find the tensions in the ropes shown in the Figure 4 if they support a 500N weight (3 significant digits).Figure 4Figure 350F T 470F T 53030F FT 1T 270F T 3w5. Each of the objects in Figure 5 below is in equilibrium. Determine the normal force N, in each case,correct to 3 significant digitsFigure 5a100N100NFigure 5bF f3030F fw=500Nw=150NFigure 5cF fw=300N

6. The Weight of W1 in the diagram below is 400N. Determine T 1 , T 2 , T 3 , and W 2All correct to 3 significant digits.T 3T 151T 235W 2 W 17. In the figure below, the two boxes have identical masses, 40 kg. Both experience a sliding frictionforce with k 0.15 . Find the acceleration of the boxes and the tension in the cord that ties themtogether (both correct to 2 significant digits).AB308. Three blocks with masses 6 kg, 9 kg, and 10 kg are connected as shown below. The coefficient offriction between the table and the 10 kg block is 0.2. (all correct to 2 significant digits)a) Find the acceleration of the systemb) The tension of the left rope.c) The tension of the right rope.10 kg6 kg9 kg

Solutions1.Question 1y50T 240T2 sin 5025 N50T2 cos5025 NxwT1wThe tension on the rope the weight hangs from is equal to the weight of the object. Therefore T 1Therefore we can find either T1or the weight w.Since this situation is in equilibrium, F 0F x0225NTcos 500Now N T2 T 25 cos 5002cos 5025NT22F y0 xand F 0 yT sin 50w025Ncos 5038.9NSubstituting this into T w we obtain N 2sin 50 0The weight of the object is 30 N38.9 sin 50w0w 29.8N w .2.Question 2yT 110100N5T 2T1 sin 10 10 5 T2 sin 5xT1 cos10T2 cos5 W=100NSince this situation is in equilibrium, F 0F x0 T T cos 5 cos 1002 10.996T0.985T02 1F y0 xand F 0 y T sin 5T sin 10100N02 10.087T 0.174T 100N02 1T 0.989TFrom first equation,2 1. Substitute into the second equation2 1T 0.989T 0.989 385N 381N0.087T 0.174T 100N012 110.087 0.989T 0.174T 100N00.260T100NT 385N1 1

3.Figure 3y30N50F fF N5030cos 50x30sin 50FW60Na) From the free body diagram, since the box is moving with constant velocity, it is in equilibrium. Weknow that F 0, therefore:xTo two significant digits, F 19b) To find the normal force,NTo two significant digits, F 37c) From the definition of , we haveKf30Ncos 50F0NFff30Ncos 5019.28NF , we use the fact that Fy0fN30 sin 50 F N 60 N 0FNN37.02N Ff19.28NK0.52F 37.02NN4.Figure 4F T 470F T 570F T 3T1T2T 460 60520 5TT20T 33030F FT 1T 2500N30T 1T 230wTTBy symmetry 1 2 T T sin 60 T sin 60500N1 22 sin 60500N250NT sin 60288.675NThe tension in T 1and T 2is 289N

TTBy symmetry 4 34T T4 1 N sin 60 cos 300T sin 60 288.675 cos 300The tension in T 3and T 4is 731NNow for T55730.951N288.675Ncos 30T4sin 205 2 3 T T sin 30Tsin 200T 288.675N sin 30730.951Ncos 200288.675N sin 30730.951N cos 20TThe tension is T 5542N55T 542.53N5aFigure 5a100NApplying Fy0F f30FN100sin 30500N0FN500N100sin 30450Nw=500N5b100N30Figure 5bApplying Fy0F fFN100sin 30150N0FN150N100sin 30200Nw=150N5cFigure 5cF fApplying Fy0w=300NFN 300cos 0FN300cos NFN 300cos 0FN300cos N

6.T 3T 1T 351T 2T 13551T 2T 235W 2 W 1W 2400N(a) (b) (c)From (c) T 1sin 35400NFrom (b) T cos513 2400NT1sin 35697.39NTT2T3cos 51571.26Ncos 51907.74NFrom (c) T2 T1cos35 N 697.39 cos 35571.26NFrom (b) T sin 51907.74Nsin 51W3 2W22W 705.45NT 697 N, T 571 N, T 908 N, W 705NTherefore :1 2 3 27.AB30F fF NF TF TF NF gF fmg cos30mgsin 30 30mgF gFf A FN A0.15mg m 0.1540kg9.82s 58.8NFf B FN B0.15 mg cos 30 m 0.1540kg9.8 0.8660252s50.922NWe need only applyx xFmafor each diagram, since masses are moving (unbalanced)

F F maTAf A xF 58.8N 40kg aTAF 40kg a 58.8NTAxxmg sin 30F F maTBf B x196N F 50.922N 40kg aTBF 40kg a 145.078NTBxxTherefore x x80kg a86.278N40kg a 58.8N 40kg a 145.078NaAlso xx89.722N80kgm1.0782sT 40kg a 58.8Nx m 40kg1.078 58.8N2 s 101.939NTherefore the masses have an acceleration of108 m s 2and a tension of 102N8.10 kg6 kg9 kgLetLetTLbe the tension in the rope on the leftTRbe the tension in the rope on the rightNow since the system is moving we will choose downward as positive in 9kg block, right as positivein the 10kg block, and up as positive in the 6kg block.For the 9kg block we have :For the 6kg block we have :For the 10kg block we have :Adding all three equations F T m ag9 R 9T F m aL g 6 6TR T LF f 10m 10ag9 g6 f10 6 9 1088.2N 58.8N 0.2 10kg m 9.8 25kg a2 s ma 0.3922sF F F m m m aThe acceleration is 0.39 m 2sNow, Subbing acceleration into the first equation to findT R

F T m ag9 R 9 m 88.2N T R9 kg 0.3922s T 85NRSubbing into the second equation to findT LT F m aLg6 6 m m TL6 kg 9.8 6kg0.3922 2 s s T 61NL