Bogoliubov Excitations of Inhomogeneous Bose-Einstein ...

More documents

Recommendations

Info

2. The Inhomogeneous Bogoliubov Hamiltonian As a matter of principle, quantum particles and quasiparticles, like electrons, photons, nucleons or atoms, are indistinguishable. Interchanging two particles may only change the many-particle wave function by a phase factor e ia , but all physical quantities stay invariant. Interchanging the particles twice recovers the initial state, such that e i2a = 1. The only two possibilities are e ia = ±1, i.e. to change or not to change sign when interchanging two particles. The former possibility is realized for fermions. For them, the antisymmetry results in the Pauli exclusion principle, forbidding more than one particle in the same single-particle state. The other possibility is realized for bosons, whose wave functions are symmetric under permutation of particles. 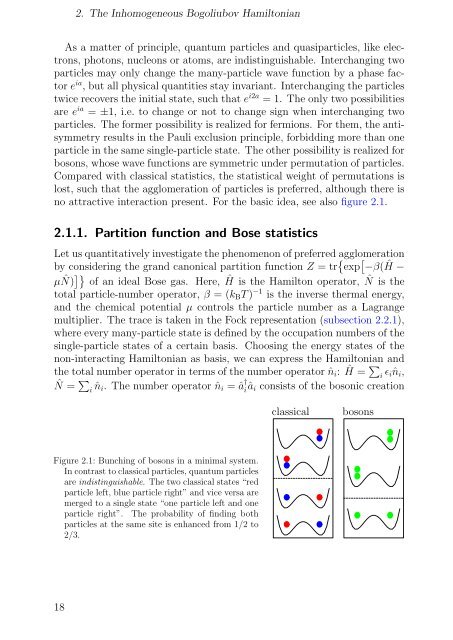Compared with classical statistics, the statistical weight of permutations is lost, such that the agglomeration of particles is preferred, although there is no attractive interaction present. For the basic idea, see also figure 2.1. 2.1.1. Partition function and Bose statistics Let us quantitatively investigate the phenomenon of preferred agglomeration by considering the grand canonical partition function Z = tr � exp � −β( ˆ H − µ ˆ N) �� of an ideal Bose gas. Here, ˆ H is the Hamilton operator, ˆ N is the total particle-number operator, β = (kBT ) −1 is the inverse thermal energy, and the chemical potential µ controls the particle number as a Lagrange multiplier. The trace is taken in the Fock representation (subsection 2.2.1), where every many-particle state is defined by the occupation numbers of the single-particle states of a certain basis. Choosing the energy states of the non-interacting Hamiltonian as basis, we can express the Hamiltonian and the total number operator in terms of the number operator ˆni: ˆ H = � i ɛiˆni, ˆN = � i ˆni. The number operator ˆni = â † i âi consists of the bosonic creation Figure 2.1: Bunching of bosons in a minimal system. In contrast to classical particles, quantum particles are indistinguishable. The two classical states “red particle left, blue particle right” and vice versa are merged to a single state “one particle left and one particle right”. The probability of finding both particles at the same site is enhanced from 1/2 to 2/3. 18 classical bosons
2.1. Bose-Einstein condensation of the ideal gas and annihilation operators â † i and âi of the corresponding state. These fulfill the bosonic commutator relations [âi, â † j ] = δij [âi, âj] = 0 = [â † i , â† j ]. (2.1) For an ideal gas of non-interacting bosons, the single-particle energy eigenstates are occupied independently and the grand canonical partition function factorizes into single-state partition functions Z = � 〈{n}| e −β( ˆ H−µ ˆ � ∞� N) |{n}〉 = e −β(ɛi−µ)ni � 1 = . 1 − e−β(ɛi−µ) {n} i ni=0 i (2.2) From the partition function, thermodynamic quantities like the average energy or the average particle number can be derived. From the total number of particles N = kBT ∂ � 1 ln(Z) = ∂µ e i β(ɛi−µ) , (2.3) − 1 the Bose occupation number ni for the state with energy ɛi is obtained as ni = 1 e β(ɛi−µ) − 1 . (2.4) The chemical potential µ has to be lower than the lowest energy level, otherwise unphysical negative occupation numbers would occur. Without loss of generality, the lowest energy level is chosen as the origin of energy ɛ0 = 0. All occupation numbers increase monotonically with µ, and the chemical potential determines � i ni = N. 2.1.2. Bose-Einstein condensation The Bose occupation numbers ni (2.4) diverge, when the chemical potential µ approaches the respective energy level ɛi from below. The chemical potential has to be lower than all energy levels, so this divergence can only happen to the occupation of the ground state. This suggests separating the total particle number N in the ground-state population n0 and the number of thermal particles NT N = n0 + NT , (2.5) with n0 = (eβ|µ| −1) −1 and NT = � i�=0 ni. Already in 1925, Einstein pointed out, that under certain conditions, the population of the thermal states NT 19
Page 1: Bogoliubov Excitations of Inhomogen
Page 5: Abstract In this thesis, different
Page 8 and 9: Contents 2.5. Exact diagonalization
Page 10 and 11: Contents Bibliography 141 List of F
Page 13 and 14: 1. Interacting Bose Gases—Complex
Page 15 and 16: 1.2. Disorder 1.2. Disorder Idealiz
Page 17 and 18: 1.4. Cold-atoms—Universal model s
Page 19 and 20: 1.5. Cold atoms—History and key e
Page 21 and 22: 1.5. Cold atoms—History and key e
Page 23 and 24: 1.6. Standing of this work are rest
Page 25: 1.6. Standing of this work The disc
Page 29: 2. The Inhomogeneous Bogoliubov Ham
Page 33 and 34: 2.1. Bose-Einstein condensation of
Page 35 and 36: 2.2. Interacting BEC and Gross-Pita
Page 41 and 42: n(x) n∞ 1 0.8 0.6 0.4 0.2 0 -3 -2
Page 43 and 44: 2.3. Bogoliubov Excitations and pha
Page 45 and 46: 2.3. Bogoliubov Excitations At high
Page 47 and 48: „ Φq ′ ¯Φ q ′ « V „ Φq
Page 49 and 50: (2) k ′ q k = ξ2 � k ′′2 +
Page 51 and 52: k k ′ 2.4.1. Single scattering se
Page 53 and 54: 2.4. Single scattering event back a
Page 55 and 56: k + − w (1) k ′ k (a) 2.4. Sing
Page 57 and 58: 2.4. Single scattering event theory
Page 59 and 60: T 1 B 2 2.5. Exact diagonalization
Page 61 and 62: 2.5. Exact diagonalization of the B
Page 69 and 70: 3. Disorder In the previous chapter
Page 71 and 72: 3.1.1. Speckle amplitude 3.1. Optic
Page 73 and 74: 3.1. Optical speckle potential In c
Page 75 and 76: 3.2. A suitable basis for the disor
Page 77 and 78: 3.2. A suitable basis for the disor
Page 79 and 80: 3.3. Effective medium and diagramma
Page 81 and 82:
3.3. Effective medium and diagramma
Page 83 and 84:
3.3. Effective medium and diagramma
Page 85 and 86:
3.4. Deriving physical quantities f
Page 87 and 88:
3.4. Deriving physical quantities f
Page 89 and 90:
Fixed particle number 3.4. Deriving
Page 91 and 92:
ρµξ d 0.2 0.15 0.1 0.05 1 2 3 4
Page 93 and 94:
4. Disorder—Results and Limiting
Page 95 and 96:
4.1. Hydrodynamic limit I: ξ = 0 t
Page 97 and 98:
4.1. Hydrodynamic limit I: ξ = 0 T
Page 99 and 100:
4.1. Hydrodynamic limit I: ξ = 0 I
Page 101 and 102:
ǫk 0.25 0.5 0.75 1 1.25 1.5 1.75 k
Page 103 and 104:
gd(κ) v 2 1.75 1.5 1.25 1 0.75 0.5
Page 105 and 106:
4.2. Hydrodynamic limit II: towards
Page 107 and 108:
∆ǫk ǫk �0.1 �0.2 �0.3 �
Page 109 and 110:
1 0.5 0 -0.5 0 20 40 60 80 100 x/σ
Page 111 and 112:
ΛN �0.1 �0.2 �0.3 �0.4 4.3
Page 113 and 114:
nnc(V )−nnc(0) nnc(0) 1.2 1.15 1.
Page 115 and 116:
4.4. Particle regime which coincide
Page 117 and 118:
4.4. Particle regime regime, becaus
Page 119 and 120:
0.02 0.015 0.01 0.005 MSg 0.01 0.1
Page 121 and 122:
5. Conclusions and Outlook (Part I)
Page 123 and 124:
5.3. Theoretical outlook potential.
Page 125:
Part II. Bloch Oscillations 113
Page 128 and 129:
6. Bloch Oscillations and Time-Depe
Page 130 and 131:
Page 132 and 133:
Page 134 and 135:
Page 136 and 137:
Page 138 and 139:
Page 140 and 141:
Page 142 and 143:
Page 144 and 145:
Page 146 and 147:
λTB t/TB 0.15 0.05 70 60 50 40 30
Page 148 and 149:
Page 150 and 151:
A. List of Symbols and Abbreviation
Page 152 and 153:
140 A. List of Symbols and Abbrevia
Page 154 and 155:
Bibliography [11] P. A. Lee and T.
Page 156 and 157:
Bibliography [35] M. Lewenstein, A.
Page 158 and 159:
Bibliography [58] J. Stenger, S. In
Page 160 and 161:
Bibliography [81] V. I. Yukalov and
Page 162 and 163:
Bibliography [108] A. Mostafazadeh,
Page 164 and 165:
Bibliography [131] F. Bloch, Über
Page 167 and 168:
Acknowledgments I thank everybody w
show all

Bogoliubov Excitations of Inhomogeneous Bose-Einstein ...

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?