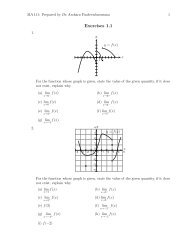
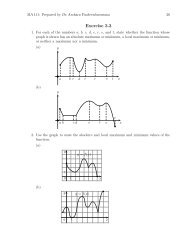
Chapter 1 Topics in Analytic Geometry

••Chapter 1Topics in Analytic Geometry1.1 Conic SectionsCircles, ellipses, parabolas, and hyperbolas are called conic sections or conics becausethey can be obtained as intersection of a plane with a double-napped circular cone. If theplane passes through the vertex of the double-napped cone, then the intersection is a point,a pair of intersection lines, or a single line. These are called degenerate conic section.Definitions of the Conic SectionsDefinition 1.1 A parabola is the set of all points in the plane that are equidistant froma fixed line and a fixed point not on the line.Vertex•focusAxisDirectrixThe line is called the directrix of the parabola, and the point is called the focus. Aparabola is symmetric about the line that passes through the focus at right angles to thedirectrix. This line, called the axis or the axis of symmetry of the parabola, intersectsthe parabola at a point called the vertex.Definition 1.2 An ellipse is the set of all points in the plane, the sum of whose distancesfrom two fixed points is a given positive constant that is greater than the distance betweenthe fixed points.1

•••••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 2The two fixed points are called the foci (plural of “focus”) of the ellipse, and themidpoint of the line segment joining the foci is called the center.• • ••Focus•Center•FocusNote that if the foci coincide, the ellipse reduces to a circle. For ellipse other than circle,the line segment through the foci and across the ellipse is called the major axis, and theline segment across the ellipse, through the center, and perpendicular to the major axis iscalled the minor axis. The endpoints of the major axis are called vertices.Minor axisVextex•VextexMajor axisDefinition 1.3 A hyperbola is the set of all points in the plane, the difference of whosedistances from two fixed distinct points is a given positive constant that is less than thedistance between the fixed points.The two fixed points are called the foci of the hyperbola. The midpoint of the linesegment joining the foci is called the center of the hyperbola. The line through the fociis called the focal axis, and the line through the center that is perpendicular to the focalaxis is called the conjugate axis. The hyperbola intersects the focal axis at two pointscalled the vertices. The two separate parts of a hyperbola are called the branches.ConjugateaxisCenterFocus FocusVertex VertexFocalaxis

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 3Associated with every hyperbola is a pair of lines, called the asymptotes of the hyperbola.This line intersect at the center of the hyperbola and have the property that as apoint P moves along the hyperbola away from the center, the vertical distance between Pand one of the asymptotes approaches zero.yxEquations of Parabolas in Standard PositionLet p denote the distance between focus and the vertex. The vertex is equidistant fromthe focus and the directrix, so the distance between the vertex and the directrix is also p;consequently, the distance between the focus and the directrix is 2p.p p• •2p2pAxisDirectrixTheequationofaparabolaissimplest ifthevertex istheoriginandtheaxisofsymmetryis along the x-axis or y-axis. The four possible such orientations are shown in Figure below.These are called the standard positions of a parabola, and the result equations are calledthe standard equations of a parabola.OrientationyStandard Equationx = −p•(p,0)xy 2 = 4px

•MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 4OrientationyStandard Equation•(−p,0)xx = py 2 = −4pxy(0,p) •xy = −px 2 = 4pyyy = px•(0,−p)x 2 = −4pyTo illustrate how the equations in the above Figure are obtained, we will derive theequation for the parabola with focus (p,0) and directrix x = −p. Let P(x,y) be any pointon the parabola.yD(−p,y)P(x,y)•F(p,0)xx = −pSince P is equidistant from the focus and directrix, the distances PF and PD in the aboveFigure are equal; that is,PF = PD (1.1)From the distance formula, the distance PF and PD arePF = √ (x−p) 2 +y 2 and PD = √ (x+p) 2 (1.2)

•••••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 5Substituting in (3.22) and squaring yieldsand after simplifying(x−p) 2 +y 2 = (x+p) 2 (1.3)y 2 = 4px (1.4)The derivations of the other equations in the previous Figure are similar.Example 1.1 Find the focus and directrix of the parabola x 2 = −6y and sketch its graph.Solution .........Example 1.2(a) Find an equation of a parabola that has vertex at the origin, opens right, and passesthrough the point P(7,−3).(b) Find the focus.Solution .........Equations of Ellipses in Standard PositionIt is traditional in the study of ellipse to denote the length of the major axis by 2a, thelength of the minor axis by 2b, and the distance between the foci by 2c.ccbbaaThe number a is called the semimajor axis and the number b the semiminor axis.There is a basic relationship between a, b, and c that can be obtained by examining thesum of the distances to the foci from a point P at the end of the major axis and from apoint Q at the end of the minor axis.√b2 +c 2Qbc c a−c√b2 +c 2•P

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 6Because P and Q both lie on the ellipse, the sum of the distances from each of them to thefoci must be equal. Thus, we obtainfrom which it follows thator equivalently2 √ b 2 +c 2 = (a−c)+(a+c)a = √ b 2 +c 2 (1.5)c = √ a 2 −b 2 (1.6)From (1.5), the distance from the focus to an end of the minor axis is a, which implied thatall points on the ellipse the sum of the distance to the foci is 2a.The equation of an ellipse is simplest if the center of the ellipse is at the origin and thefoci are on the x-axis or y-axis. The two possible such orientations are shown in Figurebelow. These are called the standard positions of an ellipse, and the result equationsare called the standard equations of an ellipse.•−a(−c,0)Orientationyb•(c,0)axStandard Equationx 2a 2 + y2b 2 = 1−bya•(0,c)−bbxx 2b 2 + y2a 2 = 1•(0,−c)−aTo illustrate how the equations in the above Figure are obtained, we will derive theequation for the ellipse with the foci on the x-axis.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 7yP(x,y))••F ′ (−c,0)•F(c,0)xLet P(x,y) be any point on the ellipse. Since the sum of the distances from P to the fociis 2a, it follows thatPF ′ +PF = 2aso√(x+c)2 +y 2 + √ (x−c) 2 +y 2 = 2aTransposing the second radical to the right side of the equation and squaring yields(x+c) 2 +y 2 = 4a 2 −4a √ (x−c) 2 +y 2 +(x−c) 2 +y 2and, on simplifying,√(x−c)2 +y 2 = a− c a xSquaring both sides again yieldswhich, by (1.5), can be written asx 2a 2 + y2a 2 −c 2 = 1x 2a + y22 b = 1 (1.7)2Conversely it can be shown that any point whose coordinates satisfying (1.7) has 2a asthe sum of its distances from the foci, so that such a point is on the ellipse.Example 1.3 Sketch the graph of the ellipseSolution .........4x 2 +18y 2 = 36.Example 1.4 Find an equation of the ellipse with foci (0,±2) and major axis with endpoints(0,±4).Solution .........

••••••••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 8Equations of Hyperbolas in Standard PositionIt is traditional in the study of hyperbola to denote the distance between the vertices by2a, the distance between the foci by 2c, and to define the quantity b asThis relationship, which can be expressed asis pictured geometrically in Figure below.b = √ c 2 −a 2 (1.8)c = √ a 2 +b 2 (1.9)accb caaThe number a is called the semifocal axis of the hyperbola and the number b the semiconjugateaxis. Moreover, for all points on a hyperbola, the distance to the farther focusminus the distance to the closer focus is 2a.The equation of a hyperbola is simplest if the center of the hyperbola is at the originand the foci are on the x-axis or y-axis. The two possible such orientations are shown inFigure below. These are called the standard positions of a hyperbola, and the resultequations are called the standard equations of a hyperbola.OrientationyStandard Equation(−c,0)ba(c,0)xx 2a 2 − y2b 2 = 1y(0,c)ab(0,−c)xy 2a 2 − x2b 2 = 1

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 9The derivation of these equations are similar to those already given for parabolas andellipses, so we will leave them as exercises.A Quick Way to Find AsymptotesThey are a trick that can be used find the equations of the asymptotes of a hyperbola.They can be obtained, when needed, by replacing 1 by 0 on the right side of the hyperbolaequation, and then solving for y in terms of x. For example, for the hyperbolawe would writex 2x 2a 2 − y2b 2 = 1a − y22 b = 0 of 2 y2 = b2which are the equations for the asymptotes.a 2 x2or y = ± b a xExample 1.5 Sketch the graph of the hyperbola9x 2 −4y 2 = 36,and showing its vertices, foci, and asymptotes.Solution .........Example 1.6 Find the equation of the hyperbola with vertices (0,±8) and asymptotes y =± 4 3 x.Solution .........Translated ConicsEquations of conic that are translated from their standard positions can be obtained byreplacing x by x − h and y by y − k in their standard equations. For a parabola, thistranslates the vertex from the origin to the point (h,k); and for ellipses and hyperbolas,this translates the center from the origin to the point (h,k).Parabolas with vertex (h,k) and axis parallel to x-axis(y −k) 2 = 4p(x−h) [Opens right](y −k) 2 = −4p(x−h) [Opens left]Parabolas with vertex (h,k) and axis parallel to y-axis(x−h) 2 = 4p(y −k)(x−h) 2 = −4p(y −k)[Opens up][Opens down]

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 10Ellipse with center (h,k) and major axis parallel to x-axis(x−h) 2a 2+(y −k)2b 2 = 1 (a > b)Ellipse with center (h,k) and major axis parallel to y-axis(x−h) 2b 2+(y −k)2a 2 = 1 (a > b)Hyperbola with center (h,k) and focal axis parallel to x-axis(x−h) 2a 2−(y −k)2b 2 = 1Hyperbola with center (h,k) and focal axis parallel to y-axis(y −k) 2a 2− (x−h)2b 2 = 1Example 1.7 Find an equation of the parabola with vertex V(−4,2) and directrix y = 5.Solution .........Sometimes the equations of translated conics occur in expanded form, in which case weare faced with the problem of identifying the graph of a quadratic equation in x and y:Ax 2 +Cy 2 +Dx+Ey +F = 0The basic procedure for determining the nature of such a graph is to complete the squaresof the quadratic terms and then try to match up the resulting equation with one of theforms of a translated conic.Example 1.8 Show that the curveis a parabola.Solution .........y = 6x 2 −12x+8Example 1.9 Discuss and sketch the graph of the equationSolution .........16x 2 +9y 2 +64x−18y−71 = 0.

•MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 11Example 1.10 Show that the curve9x 2 −4y 2 −54x−16y +29 = 0is a hyperbola. Sketch the hyperbola and show the foci, vertices, and asymptotes in thefigure.Solution .........1.2 Rotation of Axes; Second-Degree EquationsQuadratic Equations in x and yWe saw in Examples 1.8 to 1.10 that equations of the formAx 2 +Cy 2 +Dx+Ey +F = 0 (1.10)can represent conic sections. Equation (1.10) is a special case of the more general equationAx 2 +Bxy +Cy 2 +Dx+Ey +F = 0 (1.11)which, if A, B, and C are not all zero, is called a quadratic equation in x and y. IfB = 0, then (1.11) reduces to (1.10) and the conic section has its axis or axes parallel tothe coordinate axes. However, if B ≠ 0, then (1.11) contains a cross-product term Bxy,and the graph of the conic section represented by the equation has its axis or axes “tilted”relative to the coordinate axes.Rotation of AxesConsider the rotation of axes in Figure below.yy ′•(0 ′ ,y ′ )rαθP(x,y)P(x ′ ,y ′ )x ′•(x ′ ,0 ′ )xThe axes of an xy-coordinate system have been rotated about the origin through an angle θto produce a new x ′ y ′ -coordinate system. Each point P in the plane has coordinates (x ′ ,y ′ )as well as coordinates (x,y). To see how the two are related, let r be the distance from thecommon origin to the P, and let α be the angle shown in Figure. It follows thatx = rcos(θ+α), y = rsin(θ +α) (1.12)

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 12andx ′ = rcos(α), y ′ = rsin(α) (1.13)Applying the addition formulas for the sine and cosine, the relationships in (1.12) can bewritten asx = rcosθcosα−rsinθsinαy = rsinθcosα+rcosθsinαand on substituting (1.13) in these equations we obtain the following relationships calledthe rotation equations:x = x ′ cosθ−y ′ sinθ(1.14)y = x ′ sinθ +y ′ cosθExample 1.11 Suppose that the axes of an xy-coordinate system are rotated through anangle of θ = 45 ◦ to obtain an x ′ y ′ -coordinate system. Find the equation of the curvein x ′ y ′ -coordinates.Solution .........x 2 −xy +y 2 −6 = 0If the rotation (1.14) are solved for x ′ and y ′ in terms of x and y, we obtain:x ′ = xcosθ +ysinθy ′ = −xsinθ+ycosθ(1.15)Example 1.12 Find the new coordinates of the point (2,4) if the coordinate axes are rotatedthrough an angle of θ = 30 ◦ .Solution .........Eliminating the Cross-Product TermIn Example 1.11, we were able to identify the curve x 2 −xy+y 2 −6 = 0 as an ellipse becausetherotationof axes eliminate the xy-term, thereby reducing the equation to a familiar form.This occurred because the new x ′ y ′ -axes were aligned with the axes of the ellipses. Thefollows theorem tells how to determine an appropriate rotation of axes to eliminate thecross-product term of a second-degree equation in x and y.Theorem 1.1 If the equationAx 2 +Bxy +Cy 2 +Dx+Ey +F = 0 (1.16)is such that B ≠ 0, and if an x ′ y ′ -coordinate system is obtained by rotating the xy-axesthrough an angle θ satisfyingcot2θ = A−C(1.17)Bthen, in x ′ y ′ -coordinates, Equation (1.16) will have the formA ′ x ′2 +C ′ y ′2 +D ′ x ′ +E ′ y ′ +F ′ = 0

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 13Remark• It is always possible to satisfy (1.17) with an angle θ in the range 0 < θ < π/2. Weshall always use such a value of θ.• The values of sinθ and cosθ needed for the rotation equations may be obtained byfirst calculating cos2θ and then computing sinθ and cosθ from the identitiessinθ =√1−cos2θ2and cosθ =√1+cos2θ2Example 1.13 Discuss and sketch the graph of the equation xy = 1.Solution .........Example 1.14 Identify and sketch the curve41x 2 −24xy +34y 2 −25 = 0Solution .........

Chapter 2Parametric and Polar Curves2.1 Parametric Equation; TangentLinesandArc Lengthfor Parametric CurvesParametric EquationSuppose that a particle moves along a curve C in the xy-plane in such a way that x- andy-coordinates, as a functions of time, arex = f(t), y = g(t)We call these the parametric equations of motion for the particle and refer C as thetrajectory of the particle or the graph of the equations. The variable t is called theparameter for the equations.yC• (x,y)xExample 2.1 Sketch the trajectory over the time interval 0 ≤ t ≤ 10 of the particle whoseparametric equations of motion arex = t−3sint, y = 4−3cost14

•••••••••••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 15Solution One way to sketch the trajectory is to plot the (x,y) coordinate of points on thetrajectory at those times, and connect the points with a smooth curve.t x y0 0.0 1.01 -1.5 2.42 -0.7 5.23 2.6 7.04 6.3 6.05 7.9 3.16 6.8 1.17 5.0 1.78 5.0 4.49 7.8 6.710 11.6 6.5yx✠Example 2.2 Find the graph of the parametric equationsx = cost, y = sint (0 ≤ t ≤ 2π) (2.1)Solution One way to find the graph is to eliminate the parameter t by noting thatx 2 +y 2 = sin 2 t+cos 2 t = 1Thus, the graph is contained in the unit circle x 2 +y 2 = 1. Geometrically, the parametert can be interpreted as the angle swept out by the radial line from the origin to the point(x,y) = (cost,sint) on the unit circle. As t increases from 0 to 2π, the point traces thecircle counterclockwise, starting at (1,0) when t = 0 and completing one full revolutionwhen t = 2π.y1tx•(x,y)y(0,1)x✠

•••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 16OrientationThe direction inwhich thegraphof apair of parametric equations is traces asthe parameterincreasesiscalledthedirection of increasing parameter orsometimestheorientationimposed on the curve by the equation. Thus, we make a distinction between a curve, whichis the set of points, and a parametric curve, which is a curve with an orientation. Forexample, we saw in Example 3.28 that the circle represented parametrically by (2.1) istraced counterclockwise as t increases and hence has counterclockwise orientation.To obtain parametric equation for the unit circle with clockwise orientation, we canreplace t by −t in (2.1). This yieldsx = cos(−t) = cost, y = sin(−t) = −sint (0 ≤ t ≤ 2π)Here, the circle is traced clockwise by a point that starts at (1,0) when t = 0 and completesone full revolution when t = 2π.y1xty(x,y)(0,1)xExample 2.3 Graph the parametric curvex = 2t−3, y = 6t−7by eliminating the parameter, and indicate the orientation on the graph.Solution .........Expressing Ordinary Functions ParametricallyAn equation y = f(x) can be expressed in parametric form by introducing the parametert = x; this yields the parametric equationsx = t, y = f(t)For example, the portion of the curve y = cosx over the interval [−2π,2π] can be expressedparametrically asx = t, y = cost (−2π ≤ t ≤ 2π)

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 17Ifafunctionf isone-to-one,thenithasaninverse functionf −1 . Inthiscasetheequationy = f −1 (x) is equivalent to x = f(y). We can express the graph of f −1 in parametric formby introducing the parameter t = y; this yields the parametric equationsx = f(t), y = tFor example, the graph of f(x) = x 5 +x+1 can be represented parametrically asx = t, y = t 5 +t+1and the graph of f −1 can be represented parametrically asx = t 5 +t+1, y = tTangent Line to Parametric CurvesWe will be concerned with curves that are given by parametric equationsx = f(t), y = g(t)in which f(t) and g(t) have continuous first derivatives with respect to t. It can be provedthat if dx/dt ≠ 0, then y is a differentiable function of x, in which case the chain rule impliesthatdydx = dy/dt(2.2)dx/dtThis formula makes it possible to find dy/dxdirectly fromthe parametric equations withouteliminating the parameter.Example 2.4 Find the slope of the tangent line to the curveat the point where t = π/3.Solution .........x = t−3sint, y = 4−3cost (t ≥ 0)It follows from Formula (2.2) that the tangent line to a parametric curve will be horizontalat those points where dy/dt = 0 and dx/dt ≠ 0, since dy/dx = 0 at such points.Atpointswheredx/dt = 0anddy/dt ≠ 0, therightsideof (2.2)hasanonzeronumeratorand a zero denominator; we will agree that the curve has infinite slope and a verticaltangent line at such point.At points where dx/dt and dy/dt are both zero, the right side of (2.2) becomes anindeterminate form; we call such points singular points.Example 2.5 A curve C is defined by the parametric equationsx = t 2and y = t 3 −3t.Find the points on C where the tangent is horizontal or vertical.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 18Solution .........Example 2.6 The curve represented by the parametric equationsx = t 2 y = t 3 (−∞ < t < +∞)is called a semicubical parabola. The parameter t can be eliminated by cubing x andsquaring y, from which it follows that y 2 = x 3 .yxx = t 2 , y = t 3 (−∞ < t < +∞)The graph of this equation consists of two branches: an upper branch obtained by graphingy = x 3/2 and a lower branch obtained by graphing y = −x 3/2 . The two branches meet atthe origin, which corresponds to t = 0 in the parametric equations. This is a singular pointbecause the derivatives dx/dt = 2t and dy/dt = 3t 2 are both zero there. ✠Example 2.7 Without eliminating the parameter, find dy/dx and d 2 y/dx 2 at (1,1) and(1,−1) on the semicubical parabola given by the parametric equations in Example2.6Solution .........Arc Length of Parametric CurveThe following result provides a formula for finding the arc length of a curve from parametricequations for the curve.Arc Length Formula for Parametric CurveIf no segment of the curve represented by the parametric equationsx = x(t), y = y(t) (a ≤ t ≤ b)is traced more than once as t increase from a to b, and if dx/dt and dy/dt are continuousfunctions for a ≤ t ≤ b, then the arclength L of the curve is given by√∫ b (dx ) 2 ( ) 2 dyL = + dt (2.3)dt dtaExample 2.8 Find the circumference of a circle of radius a form the parametric equationsSolution .........x = acost, y = asint (0 ≤ t ≤ 2π)

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 192.2 Polar CoordinatesPolar Coordinate SystemsA polar coordinate system in a plane consists of a fixed point O, called the pole (ororigin), and a ray emanating from a pole, called the polar axis. In such a coordinatesystem we can associate with each point P in the plane a pair of polar coordinates (r,θ),where r is the distance from P to the pole and θ is an angle from the polar axis to the rayOP.P(r,θ)rθO OriginPolar axisThe number r is called the radial distance of P and the number θ the angular coordinate(or polar angle) of P.Example 2.9 Plot the points whose polar coordinates are given.(a) (3,π/4) (b) (4,2π/3) (c) (2,5π/4) (d) (4,11π/6)Solution .........The polar coordinates of a point are not unique. For example, the polar coordinatesall represent the same point.5π/3(1, 5π 3 ) −π/3(1,5π/3), (1,−π/3), (1,11π/3)(1,− π 3 ) 11π/3In general, if a point P has polar coordinates (r,θ), then(r,θ +2nπ) and(r,θ −2nπ),(1, 11π3 )are also polar coordinates of P for any nonnegative integer n.As define above, the radial coordinate r of a point P is nonnegative, since it representsthe distance from P to the pole. However, it will be convenient to allow for negativevalues of r as well. To motivate an appropriate definition, consider the point P with polarcoordinates (3,5π/4). We can reach this point by

••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 20• rotating the polar axis 5π/4 and then moving forward from the pole 3 units along theterminal side of the angle, or• rotating the polar axis π/4 and then moving backward from the pole 3 units along theextension of the terminal side.Terminal sideP(3,5π/4)5π/4Polar axisP(3,π/4)π/4Terminal sidePolar axisThis suggest that the point (3,5π/4) might also be denoted by (−3,π/4), with minussign serving to indicate that the point is on the extension of the angle’s terminal side ratherthan on the terminal side itself.In general, the terminal side of the angle θ +π is the extension of the terminal side ofθ, we define negative radial coordinates by agreeing thatto be polar coordinates for the same point.(−r,θ) and (r,θ+π)Relationship Between Polar and Rectangular CoordinatesFrequently, it will be useful to superimpose a rectangular xy-coordinate system on top ofa polar coordinate system, making the positive x-axis coincide with the polar axis. Thenevery point P will have both rectangular coordinates (x,y) and polar coordinates (r,θ).yP(r,θ) = P(x,y)ryθxxFrom the above Figure, these coordinates are related by the equationsx = rcosθ, y = rsinθ (2.4)

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 21These equation are well suited for finding x and y when r and θ are known. However, tofind r and θ when x and y are known, we use equationsr 2 = x 2 +y 2 , tanθ = y x(2.5)Example 2.10 Find the rectangular coordinates of the point P whose polar coordinates are(4,2π/3).Solution .........Example 2.11 Find polar coordinates of the point P whose rectangular coordinates are(1,−1).Solution .........Graphs in Polar CoordinatesWe will now consider the problem of graphing equations in r and θ, where θ is assumed tobe measured in radians. Some examples of such equations areExample 2.12 Sketch the graph ofr = 1, θ = π/4, r = θ, r = sinθ, r = cos2θ(a) r = 1 (b) θ = π/4Solution .........Example 2.13 Sketch the graph of r = 2cosθ in polar coordinates by plotting points.Solution .........Example 2.14 Sketch the graph of r = cos2θ in polar coordinates.Solution Instead of plotting points, we will use the graph of r = cos2θ in rectangularcoordinates to visualize how the polar graph of this equation is generated. This curve iscalled a four-petal rose.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 221r−1π2π3π2 2πy = cos2θθr varies from1 to 0 as θvaries from0 to π/4.r varies from0 to −1 as θvaries fromπ/4 to π/2.r varies from−1 to 0 as θvaries fromπ/2 to 3π/4.r varies from0 to 1 as θvaries from3π/4 to π.r varies from1 to 0 as θvaries fromπ to 5π/4.r varies from0 to −1 as θvaries from5π/4 to 3π/2.r varies from−1 to 0 as θvaries from3π/2 to 7π/4.r varies from−1 to 0 as θvaries from7π/4 to 2π.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 23Symmetry TestsObserve that the polar graph r = cos2θ in above Figure is symmetric about the x-axis andthe y-axis. This symmetry could have been predicted from the following theorem.Theorem 2.1 (Symmetry Tests).(a) A curve in polar coordinates is symmetric about the x-axis if replacing θ by −θ in itsequation produces an equivalent equation.(b) A curve in polar coordinates is symmetric about the y-axis if replacing θ by π −θ inits equation produces an equivalent equation.(c) A curve in polar coordinates is symmetric about the origin if replacing θ by θ+π, orreplacing r by −r in its equation produces an equivalent equation.π/2(r,θ)(r,π −θ)π/2(r,θ)π/2(r,θ)000(r,−θ)(r,θ+π)or(−r,θ)(a)(b)(c)Example 2.15 Show that the graph of r = cos2θ is symmetric about the x-axis and y-axis.Solution .........Families of Lines and Rays Through the PoleFor any constant θ 0 , the equationθ = θ 0 (2.6)is satisfied by the coordinates of the form P(r,θ 0 ), regardless of the value of r. Thus, theequation represents the line that passes through the pole and makes an angle of θ 0 with thepolar axis.π/2θ0θ = θ 0

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 24Families of CirclesWe will consider three families of circles in which a is assumed to be a positive constant:r = a r = 2acosθ r = 2asin2θ• The equation r = a represents a circle of radius a, centered at the pole• The equation r = 2acosθ represents a circle of radius a, centered on the x-axis andtangent to the y-axis at the origin.• The equation r = a represents a circle of radius a, centered on the y-axis and tangentto the x-axis at the origin.π/2π/2π/2r = 2asinθar = a0r = −2acosθ r = 2acosθ•(a,π)•(a,0)0•(a, π 2 )0•(a,− π 2 )r = −2asinθExample 2.16 Sketch the graphs of the following equations in polar coordinates.(a) r = 4cosθ (b) r = −5sinθ (c) r = 3Solution .........Families of Rose CurvesIn polar coordinates, equations of the formr = asinnθ or r = acosnθin which a > 0 and n is a positive integer represent families of flower-shaped curves calledroses. The rose consists of n equally spaced petals of radius a if n is odd and 2n equallyspaced petals of radius a if n is even.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 25r = asin2θ r = asin3θ r = asin4θr = asin5θr = asin6θr = acos2θ r = acos3θ r = acos4θr = acos5θr = acos6θFamilies of Cardioids and LimaconsEquations with any of the four formsr = a±bsinθr = a±bcosθin which a > 0 and b > 0 represent polar curves called limacons. There are four possibleshapes for a limacon that can be determined from the ratio a/b. If a = b (the case a/b = 1),then the limacons is called a cardioids because of its heart-shaped appearance.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 26a/b < 1a/b = 11 < a/b < 2a/b ≥ 2Limacon withinner loopCardioidDimpled limaconConvex limaconExample 2.17 Sketch the graph of the equationin polar coordinates.Solution .........Families of Spiralsr = 2(1−cosθ)A spiral is a curve that coils around a central points. The most common example is thespiral of Archimedes, which has an equation of the formr = aθ (θ ≥ 0) or r = aθ (θ ≤ 0)In these equations, θ is in radians and a is positive.Example 2.18 Sketch the graph of r = θ (θ ≥ 0) in polar coordinates by plotting points.Solution .........2.3 Tangent Lines, Arc Length, and Area for PolarCurvesTangent Lines to Polar CurvesOur first objective in this section is to find a method for obtaining slopes of tangent linesto polar curves of the form r = f(θ) in which r is a differentiable function of θ. A curve ofthis form can be expressed parametrically in terms of parameter θ by substituting f(θ) forr in the equations x = rcosθ and y = rsinθ. This yieldsx = f(θ)cosθ,y = f(θ)sinθ

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 27from which we obtaindxdθdydθ= −f(θ)sinθ+f ′ (θ)cosθ = −rsinθ+ drdθ cosθ= f(θ)cosθ+f ′ (θ)cosθ = rcosθ+ drdθ sinθThus, if dx/dθ and dy/dθ arecontinuous and if dx/dθ ≠ 0, then y is a differentiable functionof x, and Formula (2.2) with θ in place of t yieldsdydx = dy/dθ rcosθ +sinθ drdx/dθ = dθ−rsinθ +cosθ drdθ(2.7)Example 2.19 Find the slope of the tangent line to the cardioid r = 1+sinθ at the pointwhere θ = π/3.Solution .........Example 2.20 Find the points on the cardioid r = 1−cosθ at which there is a horizontaltangent line, a vertical tangent line, or a singular point.Solution .........Theorem 2.2 If the polar curve r = f(θ) passes through the origin at θ = θ 0 , and ifdr/dθ ≠ 0 at θ = θ 0 , then the line θ = θ 0 is tangent to the curve at the origin.Arc Length of a Polar CurveIf no segment of the polar curve r = f(θ) is traced more than once as θ increases from α toβ, and if dr/dθ is continuous for α ≤ θ ≤ β, then the arc length L from θ = α to θ = β isL =∫ βα√[f(θ)]2 +[f ′ (θ)] 2 dθ =∫ βα√r 2 +( ) 2 drdθ (2.8)dθExample 2.21 Find the arc length of the spiral r = e θ between θ = 0 and θ = π.Solution .........Example 2.22 Find the total arc length of the cardioid r = 1+cosθ.Solution .........

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 28Area in Polar Coordinatesr = f(θ)θ = β0Rθ = αArea Problem in Polar CoordinatesSuppose that α and β are angles that satisfy the conditionα < β ≤ α+2πand suppose that f(θ) is continuous and nonnegative for α ≤ θ ≤ β. Find the area of theregion R enclosed by the polar curve r = f(θ) and the rays θ = α and θ = β.Area in Polar CoordinatesIf α and β are angles that satisfy the conditionα < β ≤ α+2πand if f(θ) is continuous and either nonnegative or nonpositive for α ≤ θ ≤ β, then thearea A of the region R enclosed by the polar curve r = f(θ) (α ≤ θ ≤ β) and the linesθ = α and θ = β isA =∫ βα∫ β12 [f(θ)]2 1dθ =2 r2 dθ (2.9)αThe hardest part of applying (2.9) is determining the limits of integration. This can bedone as follows:Step 1 Sketch the region R whose area is to be determined.Step 2 Draw an arbitrary “radial line” from the pole to the boundary curve r = f(θ).Step 3 Ark, “Over what intervals must θ vary in order for the radial line to sweep out theregion R?”Step 4 The answer in Step 3 will determine the lower and upper limits of integration.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 29Example 2.23 Find the area of the region in the first quadrant that is within the cardioidr = 1−cosθ.Solution .........Example 2.24 Find the entire area within the cardioid of Example 2.23.Solution .........Example 2.25 Find the area enclosed by the rose curve r = cos2θ.Solution .........Example 2.26 Find the area of the region that is inside of the cardioid r = 4−4cosθ andoutside of the circle r = 6.Solution .........

Chapter 3Three-Dimensional Space; Vectors3.1 RectangularCoordinatesin3-Space; Spheres; CylindricalSurfacesRectangular Coordinate SystemsTo begin, consider three mutually perpendicular coordinate lines, called the x-axis, they-axis, and the z-axis, positioned so that their origin coincide.zOyxThe three coordinate axes form a three-dimensional rectangular coordinate system (orCartesian coordinate system) The point of intersection of the coordinate axes is calledthe origin of the coordinate system.The coordinate axes, taken in pairs, determine three coordinate planes: the xyplane,the xz-plane, and the yz-plane, which divide space into eight octants. To eachpoint P in 3-space corresponds to ordered triple of real numbers (a,b,c) which measureits directed distances from the three planes. We call a, b, and c the x-coordinate, y-coordinate, and z-coordinate of P, respectively, and we denote the point P by (a,b,c)or by P(a,b,c).The following facts about three-dimensional rectangular coordinate systems:30

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 31Region Descriptionxy-plane Consists of all points of the form (x,y,0)xz-plane Consists of all points of the form (x,0,z)yz-plane Consists of all points of the form (0,y,z)x-axis Consists of all points of the form (x,0,0)y-axis Consists of all points of the form (0,y,0)z-axis Consists of all points of the form (0,0,z)Distance in 3-Space; SpheresRecall that in 2-space the distance d between the points P 1 (x 1 ,y 1 ) and P 2 (x 2 ,y 2 ) isd = √ (x 2 −x 1 ) 2 +(y 2 −y 1 ) 2The distance formula in 3-space has the same form, but it has a third term to account forthe added dimension. The distance between the points P 1 (x 1 ,y 1 ,z 1 ) and P 2 (x 2 ,y 2 ,z 2 ) isd = √ (x 2 −x 1 ) 2 +(y 2 −y 1 ) 2 +(z 2 −z 1 ) 2Example 3.1 Find the distance d between the points (2,−3,4) and (−3,2,−5).Solution .........Recall that the standard equation of a circle in 2-space that has center (x 0 ,y 0 ) andradius r is(x−x 0 ) 2 +(y −y 0 ) 2 = r 2Analogously, standard equation of the sphere in 3-space that has center (x 0 ,y 0 ,z 0 )and radius r is(x−x 0 ) 2 +(y −y 0 ) 2 +(z −z 0 ) 2 = r 2 (3.1)Ifthetermsin(3.1)areexpandedandliketermsarecollected, thentheresultingequationhas the formx 2 +y 2 +z 2 +Gx+Hy +Iz +J = 0 (3.2)Example 3.2 Find the center and radius of the sphereSolution .........x 2 +y 2 +z 2 −10x−8y −12z +68 = 0In general, completing the squares in (3.2) produces an equation of the form(x−x 0 ) 2 +(y −y 0 ) 2 +(z −z 0 ) 2 = k 2• If k > 0, then the graph of this equation is a sphere with center (x 0 ,y 0 ,z 0 ) and radius√k.• If k = 0, then the sphere has radius zero, so the graph is the single point (x 0 ,y 0 ,z 0 ).

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 32• If k < 0, the equation is not satisfied by any values of x, y, and z, so it has no graph.Theorem 3.1 An equation of the formx 2 +y 2 +z 2 +Gx+Hy +Iz +J = 0represents a sphere, a point, or has no graph.Cylindrical SurfacesTheorem 3.2 An equation that contains only two of the variables x, y, and z represents acylindrical surface in an xyz-coordinate system. The surface can be obtained by graphingthe equation in the coordinate plane of the two variables that appear in the equation andthen translating that graph parallel to the axis of the missing variable.Example 3.3 Sketch the graph of x 2 +z 2 = 1 in 3-space.Solution .........Example 3.4 Sketch the graph of z = siny in3-space.Solution .........3.2 VectorsMany physical quantities such as area, length, mass, and temperature are completely describedonce the magnitude of the quantity is given. Such quantities are called scalar.Other physical quantities, called vectors are not completely determined until both magnitudeand a direction are specified.Vectors can be represented geometrically by arrows in 2-space or 3-space: the directionof the arrow specifies the direction of the vector and the length of the arrow describes itsmagnitude. The tail of the arrow is called the the initial point of the vector, and the tipof the arrow the terminal point.We will denote vectors with lowercase boldface type such as a, k, v, w, and x. Whendiscussing vectors, we will refer to real numbers as scalars. Scalar will be denoted bylowercase italic type such as a, k, w, and x.Two vectors, v and w, are considered to be equal (also called equivalent) if theyhave the same length and same direction, in which case we write v = w. Geometrically,two vectors are equal if they are translations of one another; thus, the three vectors in thefollowing figure are equal, even though they are in different positions.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 33If the initial point of v is A and the terminal point is B, then we write v = −→ AB whenwe want to emphasize the initial and terminal points.•BA •If the initial and terminal points of a vector coincide, then the vector has length zero;we call this the zero vector and denote it by 0. The zero vector does not have a specificdirection, so we will agree that it can be assigned any convenient direction in a specificproblem.Definition 3.1 If v and w are vectors, then the sum v+w is the vector from the initialpoint of v to the terminal point of w when the vectors are positioned so the initial point ofw is at the terminal point of v.wvv+wDefinition 3.2 If v is a nonzero vector and k is a nonzero real number (a scalar), thenthe scalar multiple kv is defined to be the vector whose length is |k| times the length ofv and whose direction is the same as that of v if k > 0 and opposite to that of v if k < 0.We define kv = 0 if k = 0 or v = 0.v2v1v 2(−1)v(− 3 2 )vObserve that if k and v are nonzero, then the vectors v and kv lie on the same line iftheir initial points coincide and lies on parallel or coincident lines if they do not. Thus, wesay that v and kv are parallel vectors. Observe also that the vector (−1)v has the samelength as v but is oppositely directed. We call (−1)v the negative of v and denote it by−v. In particular, −0 = (−1)0 = 0.Vector subtraction is defined in terms of addition and scalar multiplication byv−w = v+(−w)In the special case where v = w, their difference is 0; that is,v+(−v) = v−v = 0

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 34Vectors in Coordinate SystemsIf a vector v is positioned with its initial point at the origin of the rectangular coordinatesystem, then the terminal point will have coordinates of the form (v 1 ,v 2 ) or (v 1 ,v 2 ,v 3 ),depending on whether the vector is in 2-space or 3-space. We call these coordinates thecomponents of v, and we write v in component form using the bracket notationv = 〈v 1 ,v 2 〉 or v = 〈v 1 ,v 2 ,v 3 〉In particular, the zero vectors in 2-space and 3-space arerespectively.v = 〈0,0〉 and v = 〈0,0,0〉yz• (v 1 ,v 2 )• (v 1 ,v 2 ,v 3 )vvxyTheorem 3.3 Two vectors are equivalent if and only if their corresponding components areequal.xFor example,〈a,b,c〉 = 〈−2,3,5〉if and only if a = −2, b = 3, and c = 5.Arithmetic Operations on VectorsTheorem 3.4 If v = 〈v 1 ,v 2 〉 and w = 〈w 1 ,w 2 〉 are vectors in 2-space and k is any scalar,thenv+w = 〈v 1 +w 1 ,v 2 +w 2 〉v−w = 〈v 1 −w 1 ,v 2 −w 2 〉kv = 〈kv 1 ,kv 2 〉Similarly, if v = 〈v 1 ,v 2 ,v 3 〉 and w = 〈w 1 ,w 2 ,w 3 〉 are vectors in 3-space and k is any scalar,thenv+w = 〈v 1 +w 1 ,v 2 +w 2 ,v 3 +w 3 〉v−w = 〈v 1 −w 1 ,v 2 −w 2 ,v 3 −w 3 〉kv = 〈kv 1 ,kv 2 ,kv 3 〉

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 35Example 3.5 If v = 〈−1,2,−3〉 and w = 〈2,0,−4〉, thenv+w =3v =−2w =w−3v =Vectors With Initial Point Not At The OriginSuppose that P 1 (x 1 ,y 1 ) and P 2 (x 2 ,y 2 ) are points in 2-space and we interested in findingthe components of the vector −−→ P 1 P 2 . As illustrated in the following figure, we can write thisvector as−−→P 1 P 2 = −−→ OP 2 − −−→ OP 1 = 〈x 2 ,y 2 〉−〈x 1 ,y 1 〉 = 〈x 2 −x 1 ,y 2 −y 1 〉yP 1 (x 1 ,y 1 )•−−→OP 1−−−→P 1 P 2−−→ OP2P 2 (x 2 ,y 2 )•OThus, wehaveshownthatthecomponentsofthevector −−→ P 1 P 2 canbeobtainedbysubtractingthe coordinates of its initial point from the coordinates of its terminal point. Similarcomputations hold in 3-space, so we have established the following result.Theorem 3.5 If −−→ P 1 P 2 is a vector in 2-space with initial point P 1 (x 1 ,y 1 ) and terminal pointP 2 (x 2 ,y 2 ), then−−→P 1 P 2 = 〈x 2 −x 1 ,y 2 −y 1 〉Similarly, if −−→ P 1 P 2 is a vector in 3-space with initial point P 1 (x 1 ,y 1 ,z 1 ) and terminal pointP 2 (x 2 ,y 2 ,z 2 ), then−−→P 1 P 2 = 〈x 2 −x 1 ,y 2 −y 1 ,z 2 −z 1 〉Example 3.6 In 2-space the vector from P 1 (3,2) to P 2 (−1,4) is−−→P 1 P 2 = 〈−1−3,4−2〉 = 〈−4,2〉xand in 3-space the vector from A(1,−2,0) to B(−3,1,2) is−→AB = 〈1−(−3),−2−1,0−2〉 = 〈4,−3,−2〉✠

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 36Rules of Vector ArithmeticTheorem 3.6 For any vectors u, v, and w and any scalars k and l, the following relationshipshold:(a) u+v = v+u(b) (u+v)+w = u+(v+w)(c) u+0 = 0+u = u(d) u+(−u) = 0(e) k(lu) = (kl)u(f) k(u+v) = ku+kv(g) (k +l)u = ku+lu(h) 1u = uNorm of a VectorThe distance between the initial and terminal points of a vector v is called the length, thenorm, or the magnitude of v and is denoted by ‖v‖. This distance does not change ifthe vector is translated. The norm of a vector v = 〈v 1 ,v 2 〉 in 2-space is given by‖v‖ =√v 2 1 +v 2 2and the norm of a vector v = 〈v 1 ,v 2 ,v 3 〉 in 3-space is given by‖v‖ =√v 2 1 +v2 2 +v2 3Example 3.7 Find the norm of v = 〈4,−2〉, and w = 〈−1,3,5〉.Solution .........is,For any vector v and scalar k, the length of kv must be |k| times the length of v; that‖kv‖ = |k|‖v‖Thus, for example,‖5v‖ = |5|‖v‖ = 5‖v‖‖−3v‖ = |−3|‖v‖ = 3‖v‖‖−v‖ = |−1|‖v‖ = ‖v‖This applies to vectors in 2-space and 3-space.Unit VectorsA vector of length 1 is called a unit vector. In an xy-coordinate system the unit vectorsalong the x-axis and y-axis are denoted by i and j, respectively; and in xyz-coordinate

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 37system the unit vectors along the x-axis, y-axis and z-axis are denoted by i, j, and k,respectively.yz(0,1)(0,0,1)ji (1,0)xikj(0,1,0)yThus,x(1,0,0)i = 〈1,0〉, j = 〈0,1〉 In 2-spacei = 〈1,0,0〉, j = 〈0,1,0〉, k = 〈0,0,1〉 In 3-spaceEvery vector in 2-space is expressible uniquely in terms of i and j, and every vector in3-space is expressible uniquely in terms of i, j, and k as follows:Example 3.8v = 〈v 1 ,v 2 〉 = 〈v 1 ,0〉+〈0,v 2 〉 = v 1 〈1,0〉+v 2 〈0,1〉 = v 1 i+v 2 jv = 〈v 1 ,v 2 ,v 3 〉 = v 1 〈1,0,0〉+v 2 〈0,1,0〉+v 3 〈0,0,1〉 = v 1 i+v 2 j+v 3 k2-space〈3,−4〉 = 3i−4j3-space〈2,3,−5〉 = 2i+3j−5k〈5,0〉 = 5i+0j = 5i 〈0,0,3〉 = 3k〈0,0〉 = 0i+0j = 0 〈0,0,0〉 = 0i+0j+0k = 0(3i−2j)+(i+4j) = 2i+2j3(2i−4j) = 6i−12j(2i−j+3k)+(3i+2j−k) = i+j+2k2(3i+4j−k) = 6i+8j−2k‖3i+4j‖ = √ 3 2 +4 2 = 5 ‖2i−j+3k‖ = √ 2 2 +(−1) 2 +3 2 = √ 14‖v 1 i+v 2 j‖ = √ v 2 1 +v2 2 ‖〈v 1 ,v 2 ,v 3 〉‖ = √ v 2 1 +v2 2 +v2 3Normalizing a VectorA common problem in applications is to find a unit vector u that has the same directionas some given nonzero vector v. This can be done by multiplying v by the reciprocal of itslength; that is,u = 1‖v‖ v = v‖v‖

•MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 403.3 Dot Product; ProjectionDefinition of the Dot ProductDefinition 3.3 If u = 〈u 1 ,u 2 〉 and v = 〈v 1 ,v 2 〉 are vectors in 2-space, then the dotproduct of u and v is written as u·v and is defined asu·v = u 1 v 1 +u 2 v 2Similarly, if u = 〈u 1 ,u 2 ,u 3 〉 and v = 〈v 1 ,v 2 ,v 3 〉 are vectors in 3-space, then their dotproduct is defined asu·v = u 1 v 1 +u 2 v 2 +u 3 v 3Note that the dot product of two vectors is a scalar. For example,〈4,−3〉·〈3,2〉 = (4)(3)+(−3)(2) = 6〈1,2,−3〉·〈4,−1,2〉 = (1)(4)+(2)(−1)+(−3)(2) = −4Algebraic Properties of the Dot ProductTheorem 3.7 If u, v, and w are vectors in 2-space or 3-space and k is a scalar, then:(a) u·v = v·u(b) u·(v+w) = u·v+u·w(c) k(u·v) = (ku)·v = u·(kv)(d) v·v = ‖v‖ 2(e) 0·v = 0Angle Between VectorsSuppose that u and v are nonzero vectors in 2-space or 3-space that are positioned so theirinitial pointscoincide. Wedefine the angle between u and v tobe theangleθ determinedby the vectors that satisfies the condition 0 ≤ θ ≤ π.uθvuθvuθvuθvTheorem 3.8 If u and v are nonzero vectors in 2-space or 3-space, and if θ is the anglebetween them, thencosθ = u·v(3.5)‖u‖‖v‖

•MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 41Example 3.13 Find the angle between(a) u = 〈4,−3,−1〉 and v = 〈−2,−3,5〉(b) u = −4i+5j+k and v = 2i+3j−7k(c) u = i−2j+2k and v = −3i+6j−6kSolution .........Example 3.14 Find the angle ABC if A = (1,−2,3), B = (2,4,−6), and C = (5,−3,2).A(1,−2,3)θB(2,4,−6)C(5,−3,2)Solution .........Interpreting the Sign of the Dot ProductIt will often be convenient to express Formula (3.5) asu·v = ‖u‖‖v‖cosθ (3.6)which expresses the dot product of u and v in terms of the lengths of these vectors andthe angle between them. Since u and v are assumed to be nonzero vectors, this version ofthe formula make it clear that the sign of u·v is the same as the sign of cosθ. Thus, wecan tell from the dot product whether the angle between two vectors is acute or obtuse orwhether the vectors are perpendicular.uθvuθvuθvu·v > 0u·v < 0u·v = 0Direction AnglesIn both 2-space and 3-space the angle between a nonzero vector v and the vectors i, j,and k are called the direction angles of v, and the cosines of these angles are called thedirection cosines of v. Formulas for the direction cosines of a vector can be obtainedform Formula (3.5). For example, if v = v 1 i+v 2 j+v 3 k, thencosα = v·i‖v‖‖i‖ = v 1 v·j, cosβ =‖v‖ ‖v‖‖j‖ = v 2 v·k, cosγ =‖v‖ ‖v‖‖k‖ = v 3‖v‖

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 42yzjvkvβαixγαβjyxiTheorem 3.9 The direction cosines of a nonzero vector v = v 1 i+v 2 j+v 3 k arecosα = v 1‖v‖ , cosβ = v 2‖v‖ , cosγ = v 3‖v‖The direction cosines of a vector v = v 1 i+v 2 j+v 3 k can be computed by normalizingv and reading off the components of v/‖v‖, sincev‖v‖ = v 1‖v‖ i+ v 2‖v‖ j+ v k‖v‖ k = (cosα)i+(cosβ)j+(cosγ)kMoreover, we can show that the direction cosines of a vector satisfy the equationcos 2 α+cos 2 β +cos 2 γ = 1Example 3.15 Find the direction angles of the vector v = 4i−5j+3k.Solution .........Decomposing Vectors into Orthogonal ComponentsOur next objective is to develop a computational procedure for decomposing a vector intosum of orthogonal vectors. For this purpose, suppose that e 1 and e 2 are two orthogonalunit vectors in 2-space, and suppose that we want to express a given vector v as a sumv = w 1 +w 2so that w 1 is a scalar multiple of e 1 and w 2 is a scalar multiple of e 2 .w 2e 2ve 1 w 1

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 43That is, we want to find scalars k 1 and k 2 such thatv = k 1 e 1 +k 2 e 2 (3.7)We can find k 1 by taking the dot product of v with e 1 . This yieldsSimilarly,v·e 1 = (k 1 e 1 +k 2 e 2 )·e 1= k 1 (e 1 ·e 1 )+k 2 (e 2 ·e 1 )= k 1 ‖e 1 ‖ 2 +0 = k 1v·e 2 = (k 1 e 1 +k 2 e 2 )·e 2 = k 1 (e 1 ·e 2 )+k 2 (e 2 ·e 2 ) = 0+k 2 ‖e 2 ‖ 2 = k 2Substituting these expressions for k 1 and k 2 in (3.7) yieldsv = (v·e 1 )e 1 +(v·e 2 )e 2 (3.8)In this formula we call (v·e 1 )e 1 and (v·e 2 )e 2 the vector components of v along e 1 ande 2 , respectively; and we call v · e 1 and v · e 2 the scalar components of v along e 1 ande 2 , respectively.If θ denote the angle between v and e 1 , thenv·e 1 = ‖v‖cosθ and v·e 2 = ‖v‖sinθand the decomposition (3.7) can be expressed asExample 3.16 Letv = 〈2,3〉, e 1 =v = (‖v‖cosθ)e 1 +(‖v‖sinθ)e 2 (3.9)〈 1 √2 ,〉 〈1√ , and e 2 = −√ 1 ,2 2〉1√2Find the scalar components of v along e 1 and e 2 and the vector components of v along e 1and e 2 .Solution .........Example 3.17 A rope is attached to a 100-lb block on a ramp that is inclined at an angleof 30 ◦ with the ground.30 ◦How much force does the block exert against the ramp, and how much force must be appliedto the rope in a direction parallel to the ramp to prevent the block from sliding down theramp?Solution .........

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 44Orthogonal ProjectionsThevectorcomponentsofv alonge 1 ande 2 in(3.8)arealsocalledtheorthogonal projectionsof v on e 1 and e 2 and are denoted byproj e1v = (v·e 1 )e 1 and proj e2v = (v·e 2 )e 2In general, if e is a unit vector, then we define the orthogonal projection of v on e tobeproj e v = (v·e)e (3.10)The orthogonal projection of v on an arbitrary nonzero vector b can be obtained by normalizingb and then applying Formula (3.10); that is,( )( )b bproj b v = v·‖b‖ ‖b‖which can be rewritten asproj b v = v·b‖b‖ 2 b (3.11)Moreover, if we subtract proj b v from v, then the resulting vectorv−proj b vwill be orthogonal to b; we call this the vector component of v orthogonal to b.v−proj b vvvv−proj b vbproj b vproj b vbAcute angle between v and bObtuse angle between v and bExample 3.18 Find the orthogonal projection of v = i +j+k on b = 2i+2j, and thenfind the vector component of v orthogonal to b.Solution .........WorkRecall that we define the work W done on the object by a constant force of magnitude Facting in the direction of motion over the distance d to beW = Fd = force × distance (3.12)If we let F denote a force vector of magnitude ‖F‖ = F acting in the direction of motion,then we can write (3.12) asW = ‖F‖d

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 45Moreover, if we assume that the object moves along a line from point P to point Q, thend = ‖ −→ PQ‖, so that the work can be expressed entirely in vector form asW = ‖F‖‖ −→ PQ‖The vector −→ PQ is called the displacement vector for the object.In the case where a constant force F is not in the direction of motion, but rather makesan angle θ with the displacement vector, then we define the work W done by F to beW = (‖F‖cosθ)‖ −→ PQ‖ = F·−→ PQ (3.13)•P‖F‖FWork = ‖F‖‖ −→ PQ‖•Q•P‖F‖Fθ‖F‖cosθWork = (‖F‖cosθ)‖ −→ PQ‖•QExample 3.19 A force F = 8i + 5j in pound moves an object from P(1,0) to Q(7,1),distance measured in feet. How much work is done?Solution .........Example 3.20 A wagon is pulled horizontally by exerting a constant force of 10lb on thehandle at an angle of 60 ◦ with the horizontal. How much work is done in moving the wagon50 ft?Solution .........3.4 Cross ProductDeterminantsBefore we define the cross product, we need to define the notion of determinant.Definition 3.4 The determinant of a 2×2 matrix of real number is defined by∣ a ∣1 a 2∣∣∣= ab 1 b 1 b 2 −a 2 b 1 .2Definition 3.5 The determinant of a 3×3 matrix of real number is defined as a combinationof three 2×2 determinants, as follows:∣ a 1 a 2 a 3∣∣∣∣∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣∣ b b 1 b 2 b 3 = a 2 b 3∣∣∣∣∣∣ b1 −a 1 b 3∣∣∣∣∣∣ b∣ cc 1 c 2 c 2 c 2 +a 1 b 2∣∣∣3 c 1 c 3 (3.14)3 c 1 c 23Note that Equation (3.14) is referred to as an expansion of the determinant alongthe first row.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 46Cross ProductWe now turn to the main concept in this section.Definition 3.6 If u = 〈u 1 ,u 2 ,u 3 〉 and v = 〈v 1 ,v 2 ,v 3 〉 are vectors in 3-space, then thecross product u×v is the vector defined byu×v =∣ u ∣ 2 u 3∣∣∣i−v 2 v 3∣ u ∣ 1 u 3∣∣∣j+v 1 v 3∣ u ∣1 u 2∣∣∣k (3.15)v 1 v 2or, equivalently,u×v = (u 2 v 3 −u 3 v 2 )i−(u 1 v 3 −u 3 v 1 )j+(u 1 v 2 −u 2 v 1 )k (3.16)Observe that the right side of Formula (3.15) can be written as∣ i j k ∣∣∣∣∣u×v =u 1 u 2 u 3(3.17)∣v 1 v 2 v 3Example 3.21 Let u = 〈1,2,3〉 and v = 〈4,5,6〉. Find (a) u×v and (b) v×u.Solution .........Algebraic Properties of the Cross Product• The cross product is defined only for vectors in 3-space, whereas the dot product isdefined for vectors in 2-space and 3-space.• The cross product of two vectors is a vector, whereas the dot product of two vectorsis a scalar.The main algebraic properties of the cross product are listed in the following theorem.Theorem 3.10 If u, v, and w are any vectors in 3-space and k is any scalar, then:(a) u×v = −(v ×u)(b) u×(v+w) = (u×v)+(u×w)(c) (u+v)×w = (u×w)+(v×w)(d) k(u×v) = (ku)×v = u×(kv)(e) u×0 = 0×u = 0(f) u×u = 0

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 47The following cross products occur so frequently that it is helpful to be familiar withthem:i×j = k j×k = i k×i = j(3.18)j×i = −k k×j = −i i×k = −jThese results are easy to obtain; for example,i j k∣ ∣ ∣ ∣∣∣i×j =1 0 0∣0 1 0∣ = 0 0∣∣∣ 1 0∣ i− 1 0∣∣∣ 0 0∣ j+ 1 00 1∣ kHowever, rather than computing these cross products each time you need them, you canuse the diagram in Figure below.kijGeometric Properties of the Cross ProductThe following theorem shows that the cross product of two vectors is orthogonal to bothfactors.Theorem 3.11 If u and v are vectors in 3-space, then:(a) u·(u×v) = 0 (u×v is orthogonal to u)(b) v·(u×v) = 0 (u×v is orthogonal to v)Example 3.22 Let u and v be vectors as in Example 3.21. Show that u×v is orthogonalto both u and v.Solution .........Theorem 3.12 Let u and v be nonzero vectors in 3-space, and let θ be the angle betweenthese vectors when they are positioned so their initial points coincide.(a) ‖u×v‖ = ‖u‖‖v‖sinθ(b) The area A of the parallelogram that has u and v as adjacent sides isA = ‖u×v‖ (3.19)(c) u×v = 0 if and only if u and v are parallel vectors, that is, if and only if they arescalar multiples of one another.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 48Example 3.23 Find the area of the parallelogram with two adjacent sides formed by thevectors u = 〈1,2,−2〉 and v = 〈3,0,1〉.Solution .........Example 3.24 Find the area of the triangle that is determined by the points P 1 (2,2,0),P 2 (−1,0,2), and P 3 (0,4,3).Solution .........Scalar Triple ProductsIf u = 〈u 1 ,u 2 ,u 3 〉, v = 〈v 1 ,v 2 ,v 3 〉, and w = 〈w 1 ,w 2 ,w 3 〉 are vectors in 3-space, then thenumberu·(v×w)is called the scalar triple product of u, v, and w. This value can be obtained directlyfrom the formula∣ u 1 u 2 u 3∣∣∣∣∣u·(v×w) =v 1 v 2 v 3(3.20)∣w 1 w 2 w 3Example 3.25 Calculate the scalar triple product u·(v×w) of the vectorsSolution .........u = 3i−2j−5k, v = i+4j−4k, w = 3j+2kGeometric Properties of the Scalar Triple ProductTheorem 3.13 Let u, v and w be nonzero vectors in 3-space.(a) The volume V of the parallelepiped that has u, v and w as adjacent edges isV = |u·(v×w)| (3.21)(b) u·(v×w) = 0 if and only if u, v and w lie in the same plane.Example 3.26 Find the volume of the parallelepiped with three adjacent edges formed bythe vectors u = 〈7,8,0〉, v = 〈1,2,3〉 and w = 〈4,5,6〉.Solution .........Algebraic Properties of the Scalar Triple Productu·(v×w) = w·(u×v) = v·(w×u)u·v×w = u×v·w

••••••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 493.5 Parametric Equation of LinesLines Determined by a Point and a VectorA line in 2-space or 3-space can be determined uniquely by specifying a point on the lineand a nonzero vector parallel to the line.yzLLvP(x 0 ,y 0 )(a,b)xP 0 (x 0 ,y 0 ,z 0 )v(a,b,c)yFor example, consider a line L in 3-space that passes through the point P 0 (x 0 ,y 0 ,z 0 ) andis parallel to the nonzero vector v = 〈a,b,c〉. Then L consists precisely of those pointP(x,y,z) for which the vector −−→ P 0 P is parallel to v.zP 0 (x 0 ,y 0 ,z 0 )vxP•L(a,b,c)yxIn other words, the point P(x,y,z) is on L if and only if −−→ P 0 P is a scalar multiple of v, sayThis equation can be written aswhich implies that−−→P 0 P = tv〈x−x 0 ,y −y 0 ,z −z 0 〉 = 〈ta,tb,tc〉x−x 0 = ta, y −y 0 = tb, z −z 0 = tcThus, L can be described by the parametric equationsx = x 0 +at, y = y 0 +bt, z = z 0 +ctA similar description applies to lines in 2-space.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 50Theorem 3.14(a) The line in 2-space that passes through the point P 0 (x 0 ,y 0 ) and is parallel to thenonzero vector v = 〈a,b〉 = ai+bj has parametric equationsx = x 0 +at, y = y 0 +bt (3.22)(b) The line in 3-space that passes through the point P 0 (x 0 ,y 0 ,z 0 ) and is parallel to thenonzero vector v = 〈a,b,c〉 = ai+bj+ck has parametric equationsx = x 0 +at, y = y 0 +bt, z = z 0 +ct (3.23)Example 3.27 Find parametric equations of the line passing through the point (1,5,2) andparallel to the vector v = 〈4,3,7〉. Also, determine where the line intersects the yz-plane.Solution .........Example 3.28 Findparametricequationsof the lineLpassingthrough the pointP(1,2,−1)and Q(5,−3,4).Solution .........Example 3.29 Let L 1 and L 2 be the lines(a) Are the lines parallel?(b) Do the lines intersect?Solution .........L 1 : x = 1+4t, y = 5−4t, z = −1+5tL 2 : x = 2+8s, y = 4−3s, z = 5+sTwo lines in 3-space that are not parallel and do not intersect are called skew lines.Line SegmentsSometimes one is not interested in an entire line, but rather some segment of a line. Parametricequations of a line segment can be obtained by finding parametric equation for theentire line, then restricting the parameter appropriately so that only the desired segment isgenerated.Example 3.30 Find parametric equations describing the line segment joining the pointsP(1,2,−1) and Q(5,−3,4).Solution .........

••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 51Vector Equations of LinesWe will now show how vector notation can be used to express the parametric equations ofa line. Because two vectors are equal if and only if their components are equal, (3.22) and(3.23) can be written in vector form asor, equivalently, as〈x,y〉 = 〈x 0 +at,y 0 +bt〉〈x,y,z〉 = 〈x 0 +at,y 0 +bt,z 0 +ct〉〈x,y〉 = 〈x 0 ,y 0 〉+t〈a,b〉 (3.24)〈x,y,z〉 = 〈x 0 ,y 0 ,z 0 〉+t〈a,b,c〉 (3.25)For the equation in 2-space we define the vectors r, r 0 and v asand for the equation in 3-space we define them asr = 〈x,y〉, r 0 = 〈x 0 ,y 0 〉, v = 〈a,b〉 (3.26)r = 〈x,y,z〉, r 0 = 〈x 0 ,y 0 ,z 0 〉, v = 〈a,b,c〉 (3.27)Substituting (3.26) and (3.27) in (3.24) and (3.25), respectively, yields the equationr = r 0 +tv (3.28)in both case. We call this the vector equation of a line in 2-space or 3-space. In thisequation, v is a nonzero vector parallel to the line, and r 0 is a vector whose componentsare the coordinates of a point on the line.ytvLr 0P 0vrtvxExample 3.31 The equationis of form (3.28) with〈x,y,z〉 = 〈−1,0,2〉+t〈1,5,−4〉r 0 = 〈−1,0,2〉, v = 〈1,5,−4〉Thus, the equation represents the line in 3-space that passes through the point (−1,0,2) andis parallel to the vector 〈1,5,−4〉.✠Example 3.32 Find an equation of the line in 3-space that passes through the pointsP 1 (2,4,−1) and P 2 (5,0,7).Solution .........

•MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 523.6 Plane in 3-SpacePlane Parallel to the Coordinate PlanesThe graph of the equation x = a in an xyz-coordinate system consists of all points of theform (a,y,z), where y and z are arbitrary. One such point is (a,0,0), and all others arein the plane that passes through this point and is parallel to the yz-plane. Similarly, thegraph of y = b is the plane through (0,b,0) that is parallel to the xz-plane, and the graphof z = c is the plane through (0,0,c) that is parallel to the xy-plane.(a,0,0)x = ay = b•(0,b,0)•(0,0,c)z = cPlanes Determined by a Point and a Normal VectorA plane in 3-space can be determined uniquely by specifying a point in the plane and avector perpendicular to the plane. A vector perpendicular to the plane is called a normalto the plane.Suppose that we want to find an equation of the plane passing through P 0 (x 0 ,y 0 ,z 0 )and perpendicular to the vector n = 〈a,b,c〉. Define the vectors r 0 and r asr 0 = 〈x 0 ,y 0 ,z 0 〉 and r = 〈x,y,z〉nP 0 (x 0 ,y 0 ,z 0 ) •r−r 0 • P(x,y,z)r r 0OIt should be evident from the above Figure that the plane consists precisely of those pointsP(x,y,z) for which the vector r−r 0 is orthogonal to n; or, expressed as an equation,n·(r−r 0 ) = 0 (3.29)

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 53If preferred, we can express this vector equation in terms of components as〈a,b,c〉·〈x−x 0 ,y −y 0 ,z −z 0 〉 = 0 (3.30)from which we obtaina(x−x 0 )+b(y −y 0 )+c(z −z 0 ) = 0 (3.31)This is called the point-normal form of the equation of a plane. Formula (3.29) and(3.30) are vector version of this formula.Example 3.33 Find an equation of the plane passing through the point (1,2,3) and perpendicularto the vector n = 〈4,5,6〉.Solution .........Observe that if we multiply out the terms in (3.31) and simplify, we obtain an equationof the formax+by +cz +d = 0For example, equation in Example 3.33 can be rewritten as4x+5y +6z −32 = 0Theorem 3.15 If a, b, c, and d are constants, and a, b, and c are not all zero, then thegraph of the equationax+by +cz +d = 0 (3.32)is a plane that has the vector n = 〈a,b,c〉 as a normal.Equation (3.32) is called the general form of the equation of a plane.Example 3.34 Determine whether the planeare parallel.Solution .........3x−4y +5z = 0 and −6x+8y −10z −4 = 0Example 3.35 Find an equation of the plane through the points P 1 (1,2,2), P 2 (2,−1,4),and P 3 (3,5,−2).Solution .........Example 3.36 Determine whether the lineis parallel to the plane x−3y +5z = 12.Solution .........x = 3+8t, y = 4+5t, z = −3−tExample 3.37 Find the intersection of the line and the plane in Example 3.36.Solution .........Example 3.38 Find an equation for the plane through the point (1,4,−5) and parallel tothe plane defined by 2x−5y +7z = 12.Solution .........

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 54Intersecting PlanesTwo distinct intersecting plane determine two positive angles of intersection—an (acute)angle θ that satisfies the condition 0 ≤ θ ≤ π/2 and the supplement of that angle.n 1θn 2θθ180 ◦ −θIf n 1 and n 2 are normals to the planes, then depending on the directions of n 1 and n 2 ,the angle θ is either the angle between n 1 and n 2 or the angle between n 1 and −n 2 . In bothcase, we have the following formula for the acute angle θ between the planes:cosθ = |n 1 ·n 2 |‖n 1 ‖‖n 2 ‖(3.33)Example 3.39 Find the acute angle of intersection between the two planesSolution .........2x−4y +4z = 6 and 6x+2y −3z = 4Example 3.40 Find an equation for the line L of intersection of the planes in Example3.39.Solution .........Distance Problems Involving PlanesNext we will consider three basic distance problems in 3-space:• Find the distance between a point and a plane.• Find the distance between two parallel planes.• Find the distance between two skew lines.The three problems are related. If we can find the distance between a point and a plane,then we can find the distance between parallel planes by computing the distance betweenone of the planes and an arbitrary point P 0 in the other plane. Moreover, we can findthe distance between two skew lines by computing the distance between parallel planescontaining them.

•••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 55P•0Theorem 3.16 The distance D between a point P 0 (x 0 ,y 0 ,z 0 ) and the plane ax+by+cz+d =0 isD = |ax 0 +by 0 +cz 0 +d|√a2 +b 2 +c 2 (3.34)Example 3.41 Find the distance D between the point (1,−4,−3) and the planeSolution .........Example 3.42 The planes2x−3y +6z = −1x+2y −2z = 3 and 2x+4y −4z = 7are parallel since their normals, 〈1,2,−2〉 and 〈2,4,−4〉, are parallel vectors. Find thedistance between these planes.Solution .........Example 3.43 It was shown in Example 3.29 of Section2.5 that the lineare skew. Find the distance between them.Solution .........3.7 Quadric SurfacesQuadric SurfacesL 1 : x = 1+4t, y = 5−4t, z = −1+5tL 2 : x = 2+8s, y = 4−3s, z = 5+sIn the discussion of Formula (1.11) in Section 1.2 we noted that a second-degree equationAx 2 +Bxy +Cy 2 +Dx+Ey +F = 0represents a conic section. The analog of this equation in an xyz-coordinate system isAx 2 +By 2 +Cz 2 +Dxy +Exz +Fyz +Gx+Hy +Iz +J = 0 (3.35)which is called a second-degree equation in x, y, and z. The graphs of such equationsare called quadric surfaces or sometimes quadrics.Six common types of quadric surfaces are ellipsoids, hyperboloids of one sheet,hyperboloids of two sheet, elliptic cones, elliptic paraboloids, and hyperbolicparaboloids.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 56Techniques for Graphing Quadric SurfacesEllipsoids A sketch of an ellipsoidsx 2a + y22 b + z2= 1 (a > 0,b > 0,c > 0) (3.36)2 c2 can be obtained by first plotting the intersections with the coordinate axes, then sketchingthe elliptical traces in the coordinate planes.Notethat thecurve of intersection ofasurface with a plane iscalled the trace of thesurfacein the plane.Example 3.44 Sketch the graph of the ellipsoidSolution .........x 24 + y216 + z29 = 1Hyperboloids of One Sheet A sketch of a hyperboloid of one sheetx 2a + y22 b − z2= 1 (a > 0,b > 0,c > 0) (3.37)2 c2 can be obtained by first sketching the elliptical traces in the xy-planes, then the ellipticaltraces in the planes z = ±c, and then the hyperbolic curves that join the endpoints of theaxes of these ellipses.Example 3.45 Sketch the graph of the hyperboloid of one sheetSolution .........x 2 +y 2 − z24 = 1Hyperboloids of Two Sheet A sketch of the hyperboloid of two sheetsz 2c − x22 a − y2= 1 (a > 0,b > 0,c > 0) (3.38)2 b2 can be obtained by first plotting the intersections with the z-axis, then sketching the ellipticaltraces in the planes z = ±2c, and then sketching the hyperbolic traces that connectthe z-axis intersections and the endpoints of the axes of the ellipses.Example 3.46 Sketch the graph of the hyperboloid of two sheetsz 2 −x 2 − y24 = 1

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 57Solution .........Elliptic Cones A sketch of the elliptic conez 2 = x2a 2 + y2b 2 (a > 0,b > 0) (3.39)can be obtained by first sketching the elliptical traces in the planes z = ±1 and thensketching the linear traces that connect the endpoints of the axes of the ellipses.Example 3.47 Sketch the graph of the elliptic coneSolution .........z 2 = x 2 + y24Elliptic Paraboloids A sketch of the elliptic paraboloidz = x2a 2 + y2b 2 (a > 0,b > 0) (3.40)canbe obtainedby first sketching the elliptical traces in the planes z = 1 and then sketchingthe parabolic traces in the vertical coordinate planes to connect the origin to the ends ofthe axes of the ellipses.Example 3.48 Sketch the graph of the elliptic paraboloidSolution .........z = x24 + y29Hyperbolic Paraboloids A sketch of the hyperbolic paraboloidz = y2b 2 − x2a 2 (a > 0,b > 0) (3.41)can be obtained by first sketching the two parabolic traces that pass through the origin(one in the plane x = 0 and the other in the plane y = 0). After the parabolic traces aredraw, sketch the hyperbolic traces in the planes z = ±1 and then fill in any missing edges.Example 3.49 Sketch the graph of the hyperbolic paraboloidSolution .........z = y24 − x29

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 583.8 Cylindrical and Spherical CoordinatesIn this section we will discuss two new types of coordinate systems in 3-space that are oftenmore useful than rectangular coordinate systems for studying surfaces with symmetries.Cylindrical and Spherical Coordinate SystemsThree coordinates are required to establish the location of a point in 3-space. We havealready done this using rectangular coordinates. However, the following Figure shows twoother possibilities: part (a) of the figure shows the rectangular coordinates (x,y,z) ofa point P, part (b) shows the cylindrical coordinates (r,θ,z) of P, and part (c) showsthe spherical coordinates (ρ,θ,φ) of P.zzzy• P(x,y,z)zyxθr• P(r,θ,z)zyφρθ• P(ρ,θ,φ)yxRectangular coordinates(x,y,z)xCylindrical coordinates(r,θ,z)(r ≥ 0,0 ≤ θ < 2π)xSpherical coordinates(ρ,θ,φ)(ρ ≥ 0,0 ≤ θ < 2π,0 ≤ φ ≤ π)Constant SurfacesIn rectangular coordinates the surfaces represented by equations of the formx = x 0 , y = y 0 , and z = z 0wherex 0 ,y 0 ,andz 0 areconstant, areplanesparalleltotheyz-plane, xz-plane, andxy-plane,respectively.In cylindrical coordinates the surfaces represented by equations of the formwhere r 0 ,θ 0 , and z 0 are constant.r = r 0 , θ = θ 0 , and z = z 0• The surface r = r 0 is a right circular cylinder of radius r 0 centered on the z-axis.• The surface θ = θ 0 is a half-plane attached along the z-axis and making an angle θ 0with the positive x-axis.• The surface z = z 0 is a horizontal plane.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 59In spherical coordinates the surfaces represented by equations of the formwhere ρ 0 ,θ 0 , and φ 0 are constant.ρ = ρ 0 , θ = θ 0 , and φ = φ 0• The surface ρ = ρ 0 consists of all points whose distance ρ from the origin is ρ 0 .Assuming ρ 0 to be nonnegative, this is a sphere of radius ρ 0 centered at the origin.• As in cylindrical coordinates, the surface θ = θ 0 is a half-plane attached along thez-axis, making an angle θ 0 with the positive x-axis.• The surface φ = φ 0 consists of all point from which a line segment to the origin makesan angle of φ 0 with the positive z-axis. If 0 ≤ φ 0 < π/2, this will be the nappe ofa cone opening up, while if π/2 < φ 0 < π, this will be the nappe of a cone openingdown. (If φ 0 = π/2, then the cone is flat, and the surface is the xy-plane.)Converting CoordinatesJust as we needed to convert between rectangular and polar coordinates in 2-space, so wewill need to be able to convert between rectangular, cylindrical, and spherical coordinatesin 3-space. The following Table provides formulas for making these conversions.ConversionFormulasCylindrical to rectangular (r,θ,z) → (x,y,z) x = rcosθ,y = rsinθ,z = zRectangular to cylindrical (x,y,z) → (r,θ,z) r = √ x 2 +y 2 ,tanθ = y/x,z = zSpherical to cylindrical (ρ,θ,φ) → (r,θ,z) r = ρsinφ,θ = θ,z = ρcosφCylindrical to spherical (r,θ,z) → (ρ,θ,φ) ρ = √ r 2 +z 2 ,θ = θ,tanφ = r/zSpherical to rectangular (ρ,θ,φ) → (x,y,z) x = ρsinφcosθ,y = ρsinφsinθ,z = ρcosφRectangular to spherical (x,y,z) → (ρ,θ,φ) ρ = √ x 2 +y 2 +z 2 ,tanθ = y/x,cosφ = z/ √ x 2 +y 2 +z 2Note that r ≥ 0, ρ ≥ 0, 0 ≤ θ < 2π, 0 ≤ φ ≤ π.The diagrams in the following Figure will help you to understand how the formulas inTable are derived.xzθyr•Pz{(x,y,z)(r,θ,z)(r,θ,0)yzφθρrφ•Pz{(ρ,θ,φ)(r,θ,z)yx(a)x(b)

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 60Forexample, part (a)in the Figureshows that inconverting between rectangular coordinates(x,y,z)andcylindricalcoordinates(r,θ,z),wecaninterpret(r,θ)aspolarcoordinatesof (x,y). Thus, the polar-to-rectangular and rectangular-to-polar conversion formulas (2.4)and (2.5) of Section 2.2 provide the conversion formulas between rectangular and cylindricalcoordinates.Part (b) of Figure suggests that the spherical coordinates (ρ,θ,φ) of the point P can beconverted to cylindrical coordinates (r,θ,z) by the conversion formulasr = ρsinφ, θ = θ, z = ρcosφ (3.42)Moreover, since the cylindrical coordinates (r,θ,z) of P can be converted to rectangularcoordinates (x,y,z) by the conversion formulasx = rcosθ, y = rsinθ, z = z (3.43)we can obtain direct conversion formulas from spherical coordinates to rectangular coordinatesby substituting (3.42) in (3.43). This yieldsx = ρsinφcosθ, y = ρsinφsinθ, z = ρcosφ (3.44)The other conversion formulas in Table are left as exercises.Example 3.50(a) Find the rectangular coordinates of the point with cylindrical coordinates(r,θ,z) = (4,π/3,−3)(b) Find the rectangular coordinates of the point with spherical coordinatesSolution .........(ρ,θ,φ) = (4,π/3,π/4)Example 3.51 Find the spherical coordinates of the point that has rectangular coordinatesSolution .........(x,y,z) = (4,−4,4 √ 6)Example 3.52 Find equations of the paraboloid z = x 2 + y 2 in cylindrical and sphericalcoordinates.Solution .........

Chapter 4Vector-Valued Functions4.1 Introduction to Vector-Valued FunctionsParametric Curves in 3-SpaceRecall that if f and g are well-behaved functions, then the pair of parametric equationsx = f(t), y = g(t) (4.1)generatesacurve in2-spacethatistracedinaspecific directionastheparameter tincreases.We define this direction to be the orientation of the curve or the direction of increasingparameter, and we called the curve together with its orientation the graph of the parametricequations or the parametric curve represented by the equations. Analogously, if f, g and hare three well-behaved functions, then the parametric equationsx = f(t), y = g(t), z = h(t) (4.2)generatesacurve in3-spacethatistracedinaspecificdirectionastincreases. Asin2-space,this direction is called the orientation or direction of increasing parameter, and thecurve together with its orientation is called the graph of the parametric equations or theparametric curve represented by the equations. If no restrictions are state explicitlyor are implied by the equation, then it will be understood that t varies over the interval(−∞,+∞).Example 4.1 Describe the parametric curve represented by the equationsSolution .........x = 1−t, y = 3t, z = 2t.Example 4.2 Describe the parametric curve represented by the equationswhere a and c are positive constants.x = acosθ, y = asinθ, z = ct.61

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 62Solution As the parameter t increases, the value of z = ct also increases, so the point(x,y,z) moves upward. However, as t increases, the point (x,y,z) also moves in a pathdirectly over the circlex = acosθ, y = asinθin the xy-plane. The combination of these upward and circular motions produces a corkscrew-shaped curve that wraps around a right circular cylinder of radius a centered on thez-axis. This curve is called a circular helix.zxy✠Parametric Equations for Intersections of SurfacesCurve in 3-space often arise as intersections of surfaces. One method for finding parametricequations for the curve of intersection is to choose one of the variables as the parameter anduse the two equations to express the remaining two variables in terms of that parameter.For example, suppose we want to find parametric equations of the intersection of thecylinder z = x 3 and y = x 2 . We choose x = t as the parameter and substitute this into theequations z = x 3 and y = x 2 , then we obtain the parametric equationsThis curve is called a twisted cubic.x = t, y = t 2 , z = t 3 (4.3)

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 63Vector-Valued FunctionsThe twisted cubic defined by the equations in (4.3) is the set of points of the form (t,t 2 ,t 3 )for real values of t. If we view each of these points as a terminal point for a vector r whoseinitial point is at the origin,r = 〈x,y,z〉 = 〈t,t 2 ,t 3 〉 = ti+t 2 j+t 2 kthen we obtain r as a function of the parameter t, that is, r = r(t). Since this functionproduces a vector, we say that r = r(t) defines r as a vector-valued function of a realvariable, or more simply, a vector-valued function.If r(t) is a vector-valued function in 2-space, then for each allowable value of t the vectorr = r(t) can be represented in terms of components asr = r(t) = 〈x(t),y(t)〉 = x(t)i+y(t)jThe functions x(t) and y(t) are called the component functions or the components ofr(t). Similarly, the component functions of a vector-valued functionin 3-space are x(t), y(t) and z(t).r = r(t) = 〈x(t),y(t),z(t)〉 = x(t)i+y(t)j+z(t)kExample 4.3 The component functions ofarer(t) = 〈t,t 2 ,t 3 〉 = ti+t 2 j+t 3 kx(t) = t, y(t) = t 2 , z(t) = t 3The domain of a vector-valued function r(t) is the set of allowable values for t. If r(t)is defined in terms of component functions and the domain is not specified explicitly, thenthe domain is the intersection of the natural domains of the component functions; this iscalled the natural domain of r(t).Example 4.4 Find the natural domain ofSolution .........r(t) = 〈ln|t−1|,e t , √ t〉 = (ln|t−1|)i+e t j+ √ tkGraphs of Vector-Valued FunctionsIf r(t) is a vector-valued function in 2-space or 3-space, then we define the graph of r(t) tobe the parametric curve described by the component functions for r(t).For example, ifr(t) = 〈1−t,3t,2t〉 = (1−t)i+3tj+2tk (4.4)then the graph of r = r(t) is the graph of the parametric equationsx = 1−t, y = 3t, z = 2tThus, the graph of (4.4) is the line in Example 4.1.✠

•MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 64Example 4.5 Describe the graph of the vector-valued functionSolution .........r(t) = 〈cost,sint,t〉 = costi+sintj+tkIf a parametric curve is viewed as the graph of a vector-valued function, then we canalso imagine the graph to be traced by the tip of the moving vector. For example, if thecurve C in 3-space is the graph ofr(t) = x(t)i+y(t)j+z(t)kand if we position r(t) so its initial point is at the origin, then its terminal point will fallon the curve C.z(x(t),y(t),z(t))r(t)CyxThus, when r(t) is positioned with its initial point at the origin, its terminal point will traceout the curve C as the parameter t varies, in which case we call r(t) the radius vector orthe position vector for C.Example 4.6 Sketch the graph and a radius vector of(a) r(t) = costi+sintj, 0 ≤ t ≤ 2π(b) r(t) = costi+sintj+2k, 0 ≤ t ≤ 2πSolution .........Vector Form of a Line SegmentRecall that if r 0 is a vector in 2-space or 3-space with its initial points at the origin, thenthe line that passes through the terminal point of r 0 and is parallel to the vector v can beexpressed in vector form asr = r 0 +tvIn particular, if r 0 and r 1 are vectors in 2-space or 3-space with their initial points atthe origin, then the line that passes through the terminal points of these vectors can beexpressed in vector form asr = r 0 +t(r 1 −r 0 ) or r = (1−t)r 0 +tr 1 (4.5)

••••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 65r 0t(r 1 −r 0 )rOr 1r = (1−t)r 0 +tr 1It is common to call (4.5) the two-point vector form of a line. It is understoodin (4.5) that t varies from −∞ to +∞. However, if we restrict t to vary over the interval0 ≤ t ≤ 1, then r will vary from r 0 to r 1 . Thus, the equationr = (1−t)r 0 +tr 1 (0 ≤ t ≤ 1) (4.6)represents the line segment in 2-space or 3-space that is traced from r 0 to r 1 .4.2 Calculus of Vector-Valued FunctionsIn this section we will define limits, derivative, and integral of vector-valued functions.Limits and ContinuityOur first goal in this section is to develop a notion of what it means for a vector-valuedfunction r(t) in 2-space or 3-space to approach a limiting vector ̷L ar t approaches a numbera. That is, we want to definelimr(t) = ̷L (4.7)t→aDefinition 4.1 Let r(t) be a vector-valued function that is defined for all t in some openinterval containing the number a, except that r(t) need not be defined at a. We will writelimr(t) = ̷Lt→aif and only ifTheorem 4.1lim‖r(t)− ̷L‖ = 0t→a(a) If r(t) = 〈x(t),y(t)〉 = x(t)i+y(t)j, thenlimr(t) =t→a〈limt→ax(t),limt→ay(t)〉= limt→ax(t)i+limt→ay(t)jprovided the limits of the component functions exist. Conversely, the limits of thecomponent functions exist provided r(t) approaches a limiting vector as t approachesa.

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 66(b) If r(t) = 〈x(t),y(t),z(t)〉 = x(t)i+y(t)j+z(t)k, then〈〉limr(t) = limx(t),limy(t),limz(t)t→a t→a t→a t→a= limt→ax(t)i+limt→ay(t)j+limt→az(t)kprovided the limits of the component functions exist. Conversely, the limits of thecomponent functions exist provided r(t) approaches a limiting vector as t approachesa.Example 4.7 Find limt→0((t 2 +1)i+5costj+sintk ) .Solution .........Example 4.8 Find limt→0〈t 2 ,e t ,−2cosπt〉.Solution .........Motivated by the definition of continuity for real-valued functions, we define a vectorvaluedfunction r(t) to be continuous at t = a iflimr(t) = r(a) (4.8)t→aThat is, r(a) is defined, the limit of r(t) as t → a exists, and the two are equal. As in thecase for real-valued functions, we say that r(t) is continuous on an interval I if it iscontinuous at each point of I. It follows from Theorem 4.1 that a vector-valued function iscontinuous at t = a if and only if its component functions are continuous at t = a.DerivativesThe derivative of a vector-valued function is defined by a limit similar to that for thederivative of a real-values function.Definition 4.2 If r(t) is a vector-valued function, we define the derivative of r withrespect to t to be the vector-valued function r ′ given byr ′ (t) = limh→0r(t+h)−r(t)h(4.9)The domain of r consists of all values of t in the domain of r(t) for which the limit exists.The function r(t) is differentiable at t if the limit in (4.9) exists. All of the standardnotations for derivatives continue to apply. For example, the derivative of r(t) can beexpressed asddt [r(t)], drdt , r′ (t), or r ′

•MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 67Geometric Interpretation of the Derivative.Suppose that C is the graph of a vector-valued function r(t) in 2-space or 3-space and thatr ′ (t) exists and is nonzero for a given value of t. If the vector r ′ (t) is positioned with itsinitial point as the terminal point of the radius vector r(t), then r ′ (t) is tangent to C andpoints in the direction of increasing parameter.yr ′ (t)r(t)CxTheorem 4.2 If r(t) is a vector-valued function, then r is differentiable at t if and only ifeach of its component functions is differentiable at t, in which case the component functionsof r ′ (t) are the derivatives of the corresponding component functions of r(t).Example 4.9 Find the derivative of r(t) = sin(t 2 )i+e cost j+tlntk.Solution .........Derivative RulesMany of the rules for differentiating real-valued functions have analogs in the context ofdifferentiating vector-valued functions. We state some of these in the following theorem.Theorem 4.3 (Rules of Differentiation). Let r(t), r 1 (t), and r 2 (t) be vector-valuedfunctions that are all in 2-space or all in 3-space, and let f(t) be a real-valued function, k ascalar, and c a constant vector (that is, a vector whose value does not depend on t). Thenthe following rules of differentiation hold:(a)(b)(c)(d)(c)ddt [c] = 0ddt [kr(t)] = k d dt [r(t)]ddt [r 1(t)+r 2 (t)] = d dt [r 1(t)]+ d dt [r 2(t)]ddt [r 1(t)−r 2 (t)] = d dt [r 1(t)]− d dt [r 2(t)]ddt [f(t)r(t)] = f(t) d dt [r(t)]+r(t) d dt [f(t)]

•MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 68Tangent Lines to Graphs of Vector-Valued FunctionsDefinition 4.3 Let P be a point on the graph of a vector-valued function r(t), and let r(t 0 )be the radius vector from the origin to P.yr ′ (t 0 )r(t 0 )PTangent linexIf r ′ (t 0 ) exists and r ′ (t 0 ) ≠ 0, then we call r ′ (t 0 ) a tangent vector to the graph of r(t) atr(t 0 ), and we call the line through P that is parallel to the tangent vector the tangent lineto the graph of r(t) at r(t 0 ).Let r 0 = r(t 0 ) and v 0 = r ′ (t 0 ). Then the tangent line to the graph of r(t) at r 0 is givenby the vector equationr = r 0 +tv 0 (4.10)Example 4.10 Find parametric equations of the tangent line to the circular helixx = cost, y = sint, z = twhere t = t 0 , and use that result to find parametric equations for the tangent line at thepoint where t = π.Solution .........Example 4.11 Letandr 1 (t) = (tan −1 t)i+(sint)j+t 2 kr 2 (t) = (t 2 −t)i+(2t−2)j+(lnt)kThe graphs of r 1 (t) and r 2 (t) intersect at the origin. Find the degree measure of the acuteangle between the tangent lines to the graphs of r 1 (t) and r 2 (t) at the origin.Solution .........

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 69Derivatives of Dot and Cross ProductsThe following rules provide a method for differentiating dot products in 2-space and 3-spaceand cross product in 3-space.ddt [r 1(t)·r 2 (t)] = r 1 (t)· dr 2dt + dr 1dt ·r 2(t) (4.11)ddt [r 1(t)×r 2 (t)] = r 1 (t)× dr 2dt + dr 1dt ×r 2(t) (4.12)Theorem 4.4 If r(t) is a differentiable vector-valued function in 2-space or 3-space and‖r(t)‖ is constant for all t, thenr(t)·r ′ (t) = 0 (4.13)that is, r(t) and r ′ (t) are orthogonal vectors for all t.Definite Integrals of Vector-Valued FunctionsIf r(t) is a vector-valued function that is continuous on the interval a ≤ t ≤ b, then wedefine the definite integral of r(t) over this interval as a limit of Riemann sums, that is,In general, we have∫ ba∫ ba(∫ br(t)dt =∫ bar(t)dt =(∫ br(t)dt =aalimmax △t k →0n∑r(t ∗ k)△t k (4.14)k=1) (∫ b)x(t)dt i+ y(t)dt j 2-space (4.15)a) (∫ b) (∫ b)x(t)dt i+ y(t)dt j+ z(t)dt k 3-space (4.16)aaExample 4.12 Let r(t) = t 2 i+e t j−(2cosπt)k. EvaluateSolution .........∫ 10r(t)dt.Rules of IntegrationAs with differentiating, many of the rules for integrating real-values functions have analogsfor vector-values functions.Theorem 4.5 (Rulesof Integration). Letr(t), r 1 (t), and r 2 (t) be vector-valued functionsin 2-space or 3-space that are continuous on the interval a ≤ t ≤ b, and let k be a scalar.Then the following rules of integration hold:

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 70(a)(b)(c)∫ ba∫ ba∫ ba∫ bkr(t)dt = k r(t)dta[r 1 (t)+r 2 (t)]dt =[r 1 (t)−r 2 (t)]dt =∫ ba∫ bar 1 (t)dt+r 1 (t)dt−∫ ba∫ bar 2 (t)dtr 2 (t)dtAntiderivatives of Vector-Valued FunctionsAn antiderivative for a vector-valued function r(t) is a vector-valued function R(t) suchthatR ′ (t) = r(t) (4.17)We express Equation(4.17) using integral notation as∫r(t)dt = R(t)+C (4.18)where C represents an arbitrary constant vector. Note that the vector R(t) + C is alsocalled the indefinite integral of r(t).Since differentiation of vector-valued functions can be performed componentwise, it followsthat antidifferentiation can be done this way as well.∫Example 4.13 Evaluate the indefinite integral (2ti+3t 2 j+sin2tk)dt.Solution .........Mostofthefamiliarintegrationpropertieshavevector counterparts. Forexample, vectordifferentiation and integration are inverse operations in the sense that[∫ddt]r(t)dt = r(t) and∫r ′ (t)dt = r(t)+C (4.19)Moreover, if R(t) is an antiderivative of r(t) on an interval containing t = a and t = b, thenwe have the following vector form of the Fundamental Theorem of Calculus:∫ ba] b ∫r(t)dt = R(t) =a] br(t)dt = R(b)−R(a) (4.20)aExample 4.14 Evaluate the definite integralSolution .........∫ 10(sinπti+(6t 2 +4t)j ) dt.Example 4.15 Find r(t) given that r ′ (t) = 〈3,2t〉 and r(1) = 〈2,5〉.Solution .........

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 714.3 Change of Parameter; Arc LengthWe observed in earlier sections that a curve in 2-space or 3-space can be represented parametricallyin more than one way. Sometimes it will be desirable to change the parameter fora parametric curve to a different parameter that is better suited for the problem at hand.Smooth ParametrizationsA curve represented by r(t) is smoothly parametrized by r(t), that r(t) is a smoothfunction of t if r ′ (t) is continuous and r ′ (t) ≠ 0 for any allowable value of t. Geometrically,this means that the a smooth parametrized curve can have no abrupt changes in directionas the parameter increases.Example 4.16 Determine whether the following vector-valued functions are smooth.(a) r(t) = acosti+asintj+ctk (a > 0,c > 0)(b) r(t) = t 2 i+t 3 jSolution .........Arc Length from the Vector ViewpointRecall that the arc length L of a parametric curveis given by the formulax = x(t), y = y(t) (a ≤ t ≤ b) (4.21)L =∫ ba√ (dx ) 2+dtAnalogously, the arc length L of a parametric curvein 3-space is given by the formula( ) 2 dydt (4.22)dtx = x(t), y = y(t), z = z(t) (a ≤ t ≤ b) (4.23)L =∫ ba√ (dx ) 2+dt( ) 2 dy+dt( ) 2 dzdt (4.24)dtFormulas (4.22) and (4.24) have vector forms that we can obtain by lettingr(t) = x(t)i+y(t)j or r(t) = x(t)i+y(t)j+z(t)kIt follows thatdrdt = dx dyi+dt dt j or drdt = dx dy dzi+ j+dt dt dt k

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 72and hence√ (dx ) dr2 ∥dt∥ = +dt( ) 2 dyordt√ (dx ) dr2 ∥dt∥ = +dt( ) 2 dy+dt( ) 2 dzdtSubstituting these expressions in (4.22) and (4.24) leads us to the following theorem.Theorem 4.6 If C is the graph in 2-space or 3-space of a smooth vector-valued functionr(t), then its arc length L from t = a to t = b isL =Example 4.17 Find the arc length of the vector-valued functionfrom t = 0 to t = π.Solution .........∫ badr∥dt∥ dt (4.25)r(t) = costi+sintj+tkExample 4.18 Find the arc length of the vector-valued functionSolution .........Arc Length as a Parameterr(t) = 〈2t,lnt,t 2 〉 for 1 ≤ t ≤ e.For many purpose the best parameter to use for representing a curve in 2-space or 3-spaceparametricallyisthelengthofarcmeasured alongthecurve fromsomefixed reference point.This can be done as follows:Using Arc Length as a ParameterStep 1. Select an arbitrary point on the curve C to serve as a reference point.Step 2. Starting from the reference point, choose one direction along the curve to be thepositive direction and the other to be the negative direction.Step 3. If P is a point on the curve, let s be the signed arc length along C from thereference point to P, where s is positive if P is in the positive direction from thereference point and s is negative if P is in the negative direction.

•••••••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 73s = 3s = 2s = 1Reference points = −1s = −2s = −3CLet us now treat s as a variable. As the value of s changes, the corresponding pointP moves along C and the coordinate of P become functions of s. Thus, in 2-space thecoordinate of P are (x(s),y(s)), and in 3-space they are (x(s),y(s),z(s)). Therefore in2-space or 3-space the curve C is given by the parametric equationsx = x(s), y = y(s), or x = x(s), y = y(s), z = z(s)A parametric representation of a curve with arc length as the parameter is called an arclength parametrization of the curve.Example 4.19 Find the arc length parametrization of the circle x 2 + y 2 = a 2 with counterclockwiseorientation and (a,0) as the reference point.Solution .........Change of ParameterA change of parameter in a vector-valued function r(t) is a substitution t = g(τ) thatproduce a new vector-valued function r(g(τ)) have the same graph as r(t), but possiblytraced differently as the parameter τ increases.Example 4.20 Find a change of parameter t = g(τ) for the circlesuch thatr(t) = costi+sintj (0 ≤ t ≤ 2π)(a) the circle is traced counterclockwise as τ increases over the interval [0,1];(b) the circle is traced clockwise as τ increases over the interval [0,1].Solution .........Theorem 4.7 (Chain Rule) Let r(t) be a vector-valued function in 2-space or 3-spacethat is differentiable with respect to t. If t = g(τ) is a change of parameter in which g isdifferentiable with respect to τ, then r((g(τ)) is differentiable with respect to τ anddrdτ = dr dtdt dτ(4.26)

••MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 74A change of parameter t = g(τ) in which r(g(τ)) is smooth is called a smooth changeof parameter. Smooth change of parameter fall into two categories—those for whichdt/dτ > 0forallτ (calledpositive changes of parameter)andthoseforwhichdt/dτ < 0for all τ (called negative changes of parameter). A positive changes of parameterpreserves theorientationofaparametriccurve, andanegativechangesofparameterreversesit.Finding Arc Length ParametrizationsTheorem 4.8 Let C be the graph of a smooth vector-valued function r(t) in 2-space or 3-space, and let r 0 (t) be any point on C. Then the following formula defines a positive changeof parameter from t to s, where s is an arc length parameter having r 0 (t) as its referencepoint:∫ t∥ ∥∥∥ drs =t 0du∥ du (4.27)yr(t 0 )sr(t)CxWhen needed, Formula (4.27) can be expressed in component form ass =s =∫ t√ (dx ) 2+t 0du∫ t√ (dx ) 2+t 0du( ) 2 dy+du( ) 2 dydu 2-space (4.28)du( ) 2 dzdu 3-space (4.29)duExample 4.21 Find the arc length parametrization of the circular helixr = costi+sintj+tkthat has reference point r(0) = (1,0,0) and has the same orientation as the given helix.Solution .........Example 4.22 A bug walks along the trunk of a tree following a path modeled by thecircular helix in Example 4.21. The bug starts at the reference point (1,0,0) and walks upthe helix for a distance of 10 units. What are the bug’s final coordinates?

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 75Solution .........Example 4.23 Find the arc length parametrization of the linex = 2t+1, y = 3t−2that has the same orientation as the given line and uses (1,−2) as the reference point.Solution .........Properties of Arc Length ParametrizationsTheorem 4.9(a) If C is the graph of a smooth vector-valued function r(t) in 2-space or 3-space, wheret is a general parameter, and if s is the arc length parameter for C defined by Formula(4.27), then for every value of t the tangent vector has lengthdr∥dt∥ = ds(4.30)dt(b) If C is the graph of a smooth vector-valued function r(t) in 2-space or 3-space, wheres is an arc length parameter, then for every value of s the tangent vector to C haslengthdr∥ds∥ = 1 (4.31)(c) If C is the graph of a smooth vector-valued function r(t) in 2-space or 3-space, andif ‖dr/dt‖ = 1 for every value of t, then for any value of t 0 in the domain of r, theparameter s = t−t 0 is an arc length parameter that has its reference point at the pointon C where t = t 0 .The component forms of Formulas (4.30) and (4.31) are as follow:∥ √ (dx )ds ∥∥∥dt = dr2 dt∥ = +dt∥ √ (dx )ds ∥∥∥dt = dr2 dt∥ = +dt√ (dx ) dr2 ∥ds∥ = +ds√ (dx ) dr2 ∥ds∥ = +ds( ) 2 dy+ds( ) 2 dy+dt( ) 2 dy2-space (4.32)dt( ) 2 dz3-space (4.33)dt( ) 2 dy= 1 2-space (4.34)ds( ) 2 dz= 1 3-space (4.35)ds