Plane Geometry - Bruce E. Shapiro
Plane Geometry - Bruce E. Shapiro Plane Geometry - Bruce E. Shapiro
182 SECTION 36. TRIANGLE CENTERSFigure 36.1: The intersection of the perpendicular bisectors of the sides ofa triangle is called the orthocenter of the triangle.Thus ∠ARO = ∠CRO. But these angles are supplements, hence RO ⊥AC.Thus all three side bisectors pass through the point O. We have alreadyshown that O is equidistant from A, B, and C.Definition 36.3 Altitude. Let l be a line that is constructed perpendicularto any side of a triangle that is concurrent with the vertex V oppositethat side. Then l is said to be the line containing the altitude of thetriangle. The altitude is the distance from V to l.Theorem 36.4 The lines containing the altitudes of any triangle intersectat a point called the orthocenter.Proof. The construction is illustrated in figure 36.2. Construct line l ‖ ABthrough C; line m ‖ BC through A; and line n ‖ AC through B.Define the intersections l ∩ n = A ′ , l ∩ n = B ′ , and m ∩ n = C ′ as shownin figure 36.2.By construction, □ABA ′ C is a parallelogram, so that BA ′ = AC.By construction □C ′ BCA is a parallelogram, so that BC ′ = AC.Hence BA ′ = BC ′ , so that B is the midpoint of A ′ C ′ .Since the altitude through B is perpendicular to AC, and AC ‖ ←−→ A ′ C ′ , weconclude that the altitude through B is the perpendicular bisector of A ′ C ′ .« CC BY-NC-ND 3.0. Revised: 18 Nov 2012
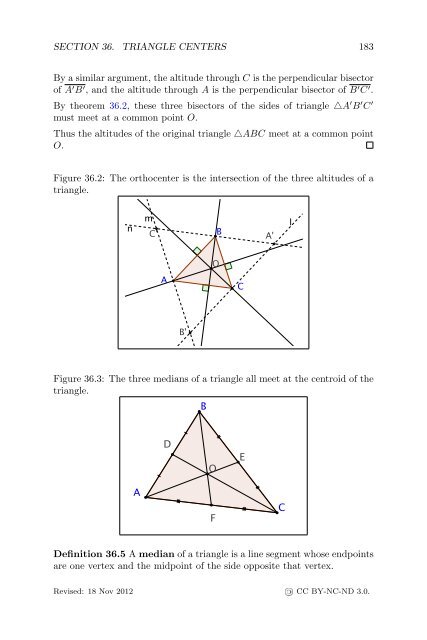
SECTION 36. TRIANGLE CENTERS 183By a similar argument, the altitude through C is the perpendicular bisectorof A ′ B ′ , and the altitude through A is the perpendicular bisector of B ′ C ′ .By theorem 36.2, these three bisectors of the sides of triangle △A ′ B ′ C ′must meet at a common point O.Thus the altitudes of the original triangle △ABC meet at a common pointO.Figure 36.2: The orthocenter is the intersection of the three altitudes of atriangle.Figure 36.3: The three medians of a triangle all meet at the centroid of thetriangle.Definition 36.5 A median of a triangle is a line segment whose endpointsare one vertex and the midpoint of the side opposite that vertex.Revised: 18 Nov 2012 « CC BY-NC-ND 3.0.
- Page 136 and 137: 132 SECTION 28. CHARACTERIZATION OF
- Page 138 and 139: 134 SECTION 29. TRANSVERSALSFigure
- Page 140 and 141: 136 SECTION 29. TRANSVERSALSCorolla
- Page 142 and 143: 138 SECTION 30. TRIANGLES IN NEUTRA
- Page 144 and 145: 140 SECTION 30. TRIANGLES IN NEUTRA
- Page 146 and 147: 142 SECTION 30. TRIANGLES IN NEUTRA
- Page 148 and 149: 144 SECTION 30. TRIANGLES IN NEUTRA
- Page 150 and 151: 146 SECTION 31. QUADRILATERALS IN N
- Page 152 and 153: 148 SECTION 31. QUADRILATERALS IN N
- Page 154 and 155: 150 SECTION 31. QUADRILATERALS IN N
- Page 156 and 157: 152 SECTION 31. QUADRILATERALS IN N
- Page 158 and 159: 154 SECTION 31. QUADRILATERALS IN N
- Page 160 and 161: 156 SECTION 32. THE EUCLIDEAN PARAL
- Page 162 and 163: 158 SECTION 32. THE EUCLIDEAN PARAL
- Page 164 and 165: 160 SECTION 32. THE EUCLIDEAN PARAL
- Page 166 and 167: 162 SECTION 32. THE EUCLIDEAN PARAL
- Page 168 and 169: 164 SECTION 32. THE EUCLIDEAN PARAL
- Page 170 and 171: 166 SECTION 32. THE EUCLIDEAN PARAL
- Page 172 and 173: 168 SECTION 33. RECTANGLESLemma 33.
- Page 174 and 175: 170 SECTION 33. RECTANGLESFigure 33
- Page 176 and 177: 172 SECTION 33. RECTANGLES« CC BY-
- Page 178 and 179: 174 SECTION 34. THE PARALLEL PROJEC
- Page 180 and 181: 176 SECTION 34. THE PARALLEL PROJEC
- Page 182 and 183: 178 SECTION 35. SIMILAR TRIANGLESBy
- Page 184 and 185: 180 SECTION 35. SIMILAR TRIANGLESCo
- Page 188 and 189: 184 SECTION 36. TRIANGLE CENTERSThe
- Page 190 and 191: 186 SECTION 36. TRIANGLE CENTERSCen
- Page 192 and 193: 188 SECTION 37. AREADefinition 37.5
- Page 194 and 195: 190 SECTION 37. AREAToday’s Lesso
- Page 196 and 197: 192 SECTION 38. THE PYTHAGOREAN THE
- Page 198 and 199: 194 SECTION 38. THE PYTHAGOREAN THE
- Page 200 and 201: 196 SECTION 38. THE PYTHAGOREAN THE
- Page 202 and 203: 198 SECTION 38. THE PYTHAGOREAN THE
- Page 204 and 205: 200 SECTION 38. THE PYTHAGOREAN THE
- Page 206 and 207: 202 SECTION 39. CIRCLESFigure 39.1:
- Page 208 and 209: 204 SECTION 39. CIRCLESFigure 39.3:
- Page 210 and 211: 206 SECTION 39. CIRCLESFigure 39.5:
- Page 212 and 213: 208 SECTION 39. CIRCLESTheorem 39.1
- Page 214 and 215: 210 SECTION 39. CIRCLESLet D be the
- Page 216 and 217: 212 SECTION 39. CIRCLES« CC BY-NC-
- Page 218 and 219: 214 SECTION 40. CIRCLES AND TRIANGL
- Page 220 and 221: 216 SECTION 40. CIRCLES AND TRIANGL
- Page 222 and 223: 218 SECTION 40. CIRCLES AND TRIANGL
- Page 224 and 225: 220 SECTION 41. EUCLIDEAN CIRCLESFi
- Page 226 and 227: 222 SECTION 41. EUCLIDEAN CIRCLESFi
- Page 228 and 229: 224 SECTION 41. EUCLIDEAN CIRCLESFi
- Page 230 and 231: 226 SECTION 41. EUCLIDEAN CIRCLESFi
- Page 232 and 233: 228 SECTION 41. EUCLIDEAN CIRCLESBy
- Page 234 and 235: 230 SECTION 42. AREA AND CIRCUMFERE
SECTION 36. TRIANGLE CENTERS 183By a similar argument, the altitude through C is the perpendicular bisectorof A ′ B ′ , and the altitude through A is the perpendicular bisector of B ′ C ′ .By theorem 36.2, these three bisectors of the sides of triangle △A ′ B ′ C ′must meet at a common point O.Thus the altitudes of the original triangle △ABC meet at a common pointO.Figure 36.2: The orthocenter is the intersection of the three altitudes of atriangle.Figure 36.3: The three medians of a triangle all meet at the centroid of thetriangle.Definition 36.5 A median of a triangle is a line segment whose endpointsare one vertex and the midpoint of the side opposite that vertex.Revised: 18 Nov 2012 « CC BY-NC-ND 3.0.