Plane Geometry - Bruce E. Shapiro

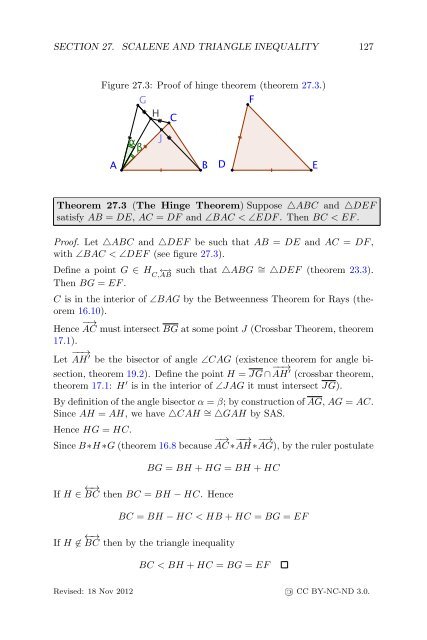
SECTION 27. SCALENE AND TRIANGLE INEQUALITY 127Figure 27.3: Proof of hinge theorem (theorem 27.3.)Theorem 27.3 (The Hinge Theorem) Suppose △ABC and △DEFsatisfy AB = DE, AC = DF and ∠BAC < ∠EDF . Then BC < EF .Proof. Let △ABC and △DEF be such that AB = DE and AC = DF ,with ∠BAC < ∠DEF (see figure 27.3).Define a point G ∈ H C,←→ ABsuch that △ABG ∼ = △DEF (theorem 23.3).Then BG = EF .C is in the interior of ∠BAG by the Betweenness Theorem for Rays (theorem16.10).Hence −→ AC must intersect BG at some point J (Crossbar Theorem, theorem17.1).Let −−→ AH ′ be the bisector of angle ∠CAG (existence theorem for angle bisection,theorem 19.2). Define the point H = JG ∩ −−→ AH ′ (crossbar theorem,theorem 17.1: H ′ is in the interior of ∠JAG it must intersect JG).By definition of the angle bisector α = β; by construction of AG, AG = AC.Since AH = AH, we have △CAH ∼ = △GAH by SAS.Hence HG = HC.Since B∗H ∗G (theorem 16.8 because −→ AC ∗ −−→ AH ∗ −→ AG), by the ruler postulateBG = BH + HG = BH + HCIf H ∈ ←→ BC then BC = BH − HC. HenceBC = BH − HC < HB + HC = BG = EFIf H ∉ ←→ BC then by the triangle inequalityBC < BH + HC = BG = EFRevised: 18 Nov 2012 « CC BY-NC-ND 3.0.