- Page 1 and 2: AN INTRODUCTION TO FUNCTIONAL PROGR
- Page 3 and 4: - 3 -LISP was one of the earliest l
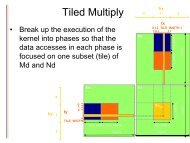
- Page 5 and 6: - 5 -1.4. Execution order in impera
- Page 7 and 8: - 7 -B[1] + B[2] + ... + B[M] + SUM
- Page 9 and 10: - 9 -quantifiers to describe proper
- Page 11 and 12: - 11 -program specification all use
- Page 13 and 14: - 13 -To begin with, we will briefl
- Page 15 and 16: - 15 -Now, compare this with the fo
- Page 17 and 18: - 17 -wherefor example: ::= λx.x
- Page 19 and 20: - 19 -giving:λx.xAn identity opera
- Page 21 and 22: - 21 -λx.xThis is now evaluated as
- Page 23: - 23 -in the body:λarg.(func arg)g
- Page 27 and 28: - 27 -and body:λsecond.firstWhen a
- Page 29 and 30: - 29 -2.12.3. Making pairs from two
- Page 31 and 32: - 31 -(λx.x λx.x) =>λx.xIt is po
- Page 33 and 34: - 33 -i) the expression is an appli
- Page 35 and 36: - 35 -((λfunc.λarg.(func arg) arg
- Page 37 and 38: - 37 -Bound variablesi) is bound i
- Page 39 and 40: - 39 -i) λx.λy.(λx.y λy.x)ii)
- Page 41 and 42: - 41 -(((cond false) true) x) ==(((
- Page 43 and 44: - 43 -3.5. OROR is a binary operato
- Page 45 and 46: - 45 -two ==(succ one) ==(λn.λs.(
- Page 47 and 48: - 47 -So:def pred = λn.(((cond zer
- Page 49 and 50: - 49 -For example, we could re-writ
- Page 51 and 52: - 51 -4) Show that:λx.(succ (pred
- Page 53 and 54: - 53 -gobble a sweet andgobble a sw
- Page 55 and 56: - 55 -then xelse f (succ x) (pred y
- Page 57 and 58: - 57 -and:-> ... ->will still imply
- Page 59 and 60: - 59 -If this function is now appli
- Page 61 and 62: - 61 -def add1 f x y =if iszero yth
- Page 63 and 64: - 63 -the second minus the first wi
- Page 65 and 66: - 65 -succ (succ (div1 one four)) -
- Page 67 and 68: - 67 -n * n-1 * n-2 * ... * 1in nor
- Page 69 and 70: - 69 -within our intended interpret
- Page 71 and 72: - 71 -Sometimes it may be necessary
- Page 73 and 74: - 73 -λvalue.λs.(s error_type val
- Page 75 and 76:
- 75 -def AND X Y =if and (isbool X
- Page 77 and 78:
- 77 -def ISBOOL B = MAKE_BOOL (isb
- Page 79 and 80:
- 79 -Note that we return NUMB_ERRO
- Page 81 and 82:
- 81 -def ’1’ = MAKE_CHAR (succ
- Page 83 and 84:
- 83 -will do so. However, for a no
- Page 85 and 86:
- 85 -To simplify the presentation
- Page 87 and 88:
- 87 -rec 0 = or (SUCC ) = Thus,
- Page 89 and 90:
- 89 -def signed_type = ...def SIGN
- Page 91 and 92:
- 91 -If the head of a list and the
- Page 93 and 94:
- 93 -def MAKE_LIST = make_obj list
- Page 95 and 96:
- 95 -LIST_ERRORThe test for an emp
- Page 97 and 98:
- 97 -CONS 1 (APPEND (TAIL (CONS 1
- Page 99 and 100:
- 99 -For example:1::(2::(3::(4::[]
- Page 101 and 102:
- 101 -LIST_EQUAL [] [] = TRUELIST_
- Page 103 and 104:
- 103 -In general, the string:" "is
- Page 105 and 106:
- 105 -(STRING_LESS (’r’::"ridg
- Page 107 and 108:
- 107 -gives value of "" with 10*(1
- Page 109 and 110:
- 109 -In general, for:rec =IF IS
- Page 111 and 112:
- 111 -Note that this description t
- Page 113 and 114:
- 113 -Similarly, to remove a speci
- Page 115 and 116:
- 115 -rec DOUBLE [] = []or DOUBLE
- Page 117 and 118:
- 117 -"cats"::"dogs"::(λW.(APPEND
- Page 119 and 120:
- 119 -‘TAIL ’>6.18. Exercises1
- Page 121 and 122:
- 121 -["Betty","Baker"].For exampl
- Page 123 and 124:
- 123 -For example:IF STRING_EQUAL
- Page 125 and 126:
- 125 -["VDU",25,12]::["modem",20,1
- Page 127 and 128:
- 127 -matches the argument:so:[,,]
- Page 129 and 130:
- 129 -For example, suppose we have
- Page 131 and 132:
- 131 -to place the Nth item, skip
- Page 133 and 134:
- 133 -[7,EMPTY,EMPTY]To add 4 to t
- Page 135 and 136:
- 135 -[3,EMPTY,EMPTY],[5,EMPTY,[6,
- Page 137 and 138:
- 137 -TFIND 5 [4,[3,EMPTY,EMPTY],[
- Page 139 and 140:
- 139 -7.14. Binary tree efficiency
- Page 141 and 142:
- 141 -λ[a,b].(SUM_SQ2 a b)so:def
- Page 143 and 144:
- 143 -and so on.def istype (t::o)=
- Page 145 and 146:
- 145 - ::= ( + ) |( + ) |( + ) |(
- Page 147 and 148:
- 147 -IF ISZERO (ADD 1 2)THEN 1ELS
- Page 149 and 150:
- 149 -cond one (add (succ one) (pr
- Page 151 and 152:
- 151 -λdummy.e2Instead, we have t
- Page 153 and 154:
- 153 -The first Church-Rosser theo
- Page 155 and 156:
- 155 -(λx.x λy.y) 2=>λy.yand th
- Page 157 and 158:
- 157 -For example, consider:SQUARE
- Page 159 and 160:
- 159 -SQUARE 1 => ... =>IFIND 1 SQ
- Page 161 and 162:
- 161 - : For objects which do not
- Page 163 and 164:
- 163 -is a tuple consisting of two
- Page 165 and 166:
- 165 -to indicate both integer and
- Page 167 and 168:
- 167 -- tl;> fn : (’a list) -> (
- Page 169 and 170:
- 169 -Functions have the form:fn
- Page 171 and 172:
- 171 -For example, to find the lar
- Page 173 and 174:
- 173 -9.19. Pattern matchingSML fu
- Page 175 and 176:
- 175 -end;> val sort = fn : (int l
- Page 177 and 178:
- 177 -- fun length [] = 0 |length
- Page 179 and 180:
- 179 -- datatype traffic_light = r
- Page 181 and 182:
- 181 -but this defines the new typ
- Page 183 and 184:
- 183 -con empty = empty : (’a tr
- Page 185 and 186:
- 185 -iv)Join strings s1 and s2 to
- Page 187 and 188:
- 187 -( + )( - )( * )( / ) == numb
- Page 189 and 190:
- 189 -10.4. Logictis the primitive
- Page 191 and 192:
- 191 -(> 9 8 7 6 5) ->tThe primiti
- Page 193 and 194:
- 193 -It is important to note that
- Page 195 and 196:
- 195 -nilwhich may be also written
- Page 197 and 198:
- 197 -(car ’(1 2 3)) ->1(cdr ’
- Page 199 and 200:
- 199 -(tadd 7 nil) ->(7 nil nil)(t
- Page 201 and 202:
- 201 -For example, suppose the ave
- Page 203 and 204:
- 203 -10.17. Symbols, quoting and
- Page 205 and 206:
- 205 -Note once again that there m
- Page 207 and 208:
- 207 -iv) find the sum of applying
- Page 209 and 210:
- 209 -ii) Write a function which i
- Page 211 and 212:
- 211 -Chapter 3 - Conditions, bool
- Page 213 and 214:
- 213 -11. R. M. Burstall, J. S. Co
- Page 215 and 216:
- 215 -55. P. Wegner, Programming L
- Page 217 and 218:
- 217 - - (g h) - - g - - h - f
- Page 219 and 220:
- 219 -λb.b3)i) a) (identity ) =>
- Page 221 and 222:
- 221 -λb.(λa.{a} b))λa.{a}a fre
- Page 223 and 224:
- 223 -not (or false false) => ...
- Page 225 and 226:
- 225 -false (implies false true) f
- Page 227 and 228:
- 227 -then fun nelse add (fun n) (
- Page 229 and 230:
- 229 -i) ISBOOL 3 => ... =>MAKE_BO
- Page 231 and 232:
- 231 -iii)def SIGN_+ X Y =if and (
- Page 233 and 234:
- 233 -THEN [H,M,S]ELSElet M = M +
- Page 235 and 236:
- 235 -λy.y5 reductionsλf.λa.(f
- Page 237 and 238:
- 237 -gconstr (v:int) ((h::t):int
- Page 239 and 240:
- 239 -0(+ n (nsum (- n 1)))))ii) (
- Page 241:
- 241 -(if (= m1 m2)(if (< s1 s2)tn