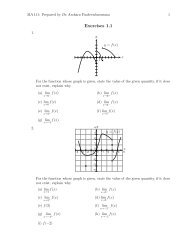
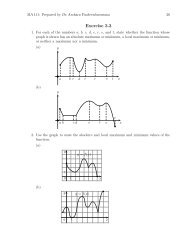
Chapter 1 Topics in Analytic Geometry

MA112 Section 750001: Prepared by Dr.Archara Pacheenburawana 67(b) If r(t) = 〈x(t),y(t),z(t)〉 = x(t)i+y(t)j+z(t)k, then〈〉limr(t) = limx(t),limy(t),limz(t)t→a t→a t→a t→a= limt→ax(t)i+limt→ay(t)j+limt→az(t)kprovided the limits of the component functions exist. Conversely, the limits of thecomponent functions exist provided r(t) approaches a limiting vector as t approachesa.Example 4.7 Find limt→0((t 2 +1)i+5costj+sintk ) .Solution .........Example 4.8 Find limt→0〈t 2 ,e t ,−2cosπt〉.Solution .........Motivated by the definition of continuity for real-valued functions, we define a vectorvaluedfunction r(t) to be continuous at t = a iflimr(t) = r(a) (4.8)t→aThat is, r(a) is defined, the limit of r(t) as t → a exists, and the two are equal. As in thecase for real-valued functions, we say that r(t) is continuous on an interval I if it iscontinuous at each point of I. It follows from Theorem 4.1 that a vector-valued function iscontinuous at t = a if and only if its component functions are continuous at t = a.DerivativesThe derivative of a vector-valued function is defined by a limit similar to that for thederivative of a real-values function.Definition 4.2 If r(t) is a vector-valued function, we define the derivative of r withrespect to t to be the vector-valued function r ′ given byr ′ (t) = limh→0r(t+h)−r(t)h(4.9)The domain of r consists of all values of t in the domain of r(t) for which the limit exists.The function r(t) is differentiable at t if the limit in (4.9) exists. All of the standardnotations for derivatives continue to apply. For example, the derivative of r(t) can beexpressed asddt [r(t)], drdt , r′ (t), or r ′