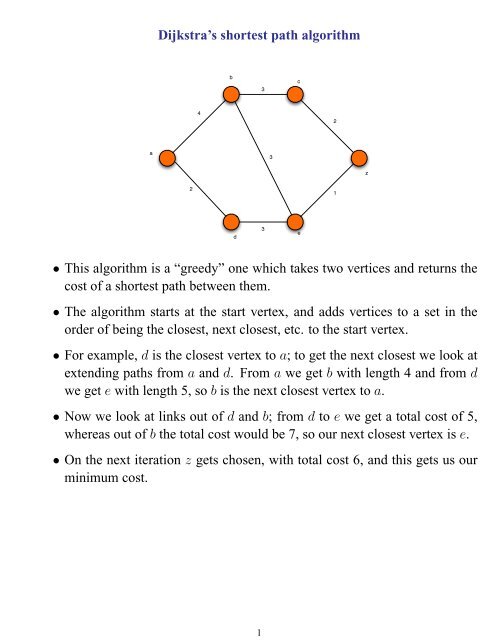
Dijkstra's shortest path algorithm • This algorithm is a “greedy” one ...

The inductive step of Dijkstra• The IH: Assume for n = k:1. for each t ∈ S, L k (t) is the length of a shortest path from s to t; and2. for v ∈ Q, L k (v) is the length of a shortest path from s to v that liestotally in S except for v itself.• Prove (1) for n = k + 1. Suppose u is added to S at the (k + 1)-st iteration.Before this iteration, L k (u) is the length of a shortest path to u lying totallyis S except for u itself. We have L k+1 (u) = min{L k (v) : v /∈ S}. We claimthat L k+1 (u) is the length of a shortest path from s to u. For if not, theremust be a shorter path to u exiting S at some vertex p ∈ S, on one step outof S for the first time to some v ≠ u. From part (2) of the IH we have L k (v)is the length of a shortest path from a to v lying in S except for v. We alsohave L k (v) < L k (u), because if L k (v) ≥ L k (u), then the “shortest” pathlength from a (through v) to u would be greater than the length of the pathfrom a to u remaining in S except for u, that is L k (u). But this contradictsthe choice of u having the minimum L k value. This proves the claim.• Prove (2) for n = k + 1. Let p ∈ Q after iteration k + 1. A shortest paththrough (the new) S to p either goes through u as the last vertex in s or not.In the first case its length is L k (p). In the second case it is L k (u) + w(u, p).So its length is min{L k (p), L k (u) + w(u, p)}.5

Improving the complexity of DIJKSTRA• We can do better than running through all of Q to find and remove theelement of Q with minimum L value, in case the graph G = (V, E) issparse – each vertex is of low degree.• We realize Q not with a table, but with a heap. This is a (complete) binarytree whose nodes are labeled with L-values in such a way that each nodevalue is less than that of its immediate descendants.7

Ultimate effect on complexity of DIJKSTRA• Let G = (V, E).• EXTRACT-MIN takes O(log |V |) time, and there are |V | such operations.• Building the heap in the first place takes O(|V |).• Can do the step of setting vertices v /∈ S with an edge to the current u tomin{L(v), L(u) + w(u, v)}, in O(|E| log |V |) (not shown).• Total time is then O(|E| log |V |). Thus if the graph is sparse (say a constantnumber of edges per node, so |E| = O(|V |), we can get the time down toO(|V | log |V |).11

Priority Queues• A priority queue is a list of items in which each item has associated with ita priority. In general, different items may have different priorities and wespeak of one item having a higher priority than another. Given such a listwe can determine which is the highest (or the lowest) priority item in thelist. Items are inserted into a priority queue in any, arbitrary order. However,items are withdrawn from a priority queue in order of their prioritiesstarting with the highest (lowest) priority item first.• For example, consider the software which manages a printer. In general, itis possible for users to submit documents for printing much more quicklythan it is possible to print them. A simple solution is to place the documentsin a FIFO queue. In a sense this is fair, because the documents are printedon a first-come, first-served basis.• However, a user who has submitted a short document for printing willexperience a long delay when much longer documents are already in thequeue. An alternative solution is to use a priority queue in which the shortera document, the higher its priority. By printing the shortest documents first,we reduce the level of frustration experienced by the users. In fact, it canbe shown that printing documents in order of their length minimizes theaverage time a user waits for her document.• Removing a job with the smallest number of pages can be done with EXTRACT-MIN.• You also need to be able to insert a new item into the queue (e.g., whenfirst building the set Q in Dijkstra).12

Insertion Operation• Insert 14; make a “hole” at the end of the array• Move the hole up to the “proper” position, then insert the 1413

Floyd-Warshall for the all-pairs shortest path• For Kevin Bacon numbers we ran FLOYD-WARSHALL. This used a matrixW.• Let the initial entries of W be integers representing path lengths: W [i, j] =w(i, j). This assumes you number the vertices.• The code for finding the length of the shortest path between any two verticesisinitialize Wfor j = 1 to ndo for i, k = 1 to ndo W(i, k) ← min(W(i, k), W(i, j) + W(j, k))• The complexity is O(n 3 ). Clearly to find a shortest path from a to z weshould use DIJKSTRA.• What about correctness?• Recall that just before iteration j, the number W j (i, k) is the shortest pathlength from i to k for a path whose interior vertices are in {1, . . . , j − 1}.This we use for our inductive statement.14

Proving correctness of FLOYD-WARSHALL• The inductive statement: just before iteration j, the number W j (i, k) is theshortest path length from i to k for a path whose interior vertices are in{1, . . . , n − 1}.• We start with n = 1. By convention, {1, −1} = ∅. The statement then saysthat the length of the shortest path between any two adjacent points u andv is w(u, v), which is true.• Assume the statement for n = j and prove it for n = j + 1. The new valueW j+1 (i, k) is min(W j (i, k), W j (i, j) + W j (j, k)). We need to show thisis the correct value. A shortest path from i to k whose interior vertices arein {i, . . . , j} either goes through j or not. If not, its length is W j (i, k), byinductive hypothesis. Otherwise it goes through j, and clearly not morethan once through j. So it can be broken into two parts, one part a shortestpath from i to j with interior vertices in {1, . . . , j −1} and another shortestpath from j to k, again with interior vertices in {1, . . . , j − 1}. The lengthof this is W j (i, j)+W j (j, k), again by inductive hypothesis. So the correctlength is min(W j (i, k), W j (i, j) + W j (j, k)), as the algorithm stipulates,and this completes the induction.• FLOYD-WARSHALL is a dynamic programming algorithm.15

What’s coming up after 203?• EECS 281 is about algorithms and data structures. You learn about concretestorage structures like linked lists, arrays, and the like.• You also learn about more abstract structures such as priority queues.• Ideally with these abstract structures, you can define them using structuralinduction, and prove properties about them the same way.• An example would be “binary trees”.• EECS 376 is about models of computation. You learn about finite-statemachines, which are really useful in modelling all sorts of computationalsystems.• You also learn about undecidability, uncomputability, and computationalcomplexity, including more about P and NP.16

How do you prove that there isn’t any algorithm to solve a problem?• The basic method is to prove it by contradiction.• The method also assumes that algorithms can all be coded as programs ina single programming language.• It then uses the fact that all programs are just strings over an alphabet.• It is assumed that (arbitrary length) strings are a datatype in the programminglanguage.• We then consider a specific property P of programs. The set of strings representingprograms with that property, as it turns out, cannot be recognizedby any one program in the language. Since each algorithm is representableby one program in the language, this means that no algorithm can solve thequestion: does a given program have property P ?• What’s the magic property P ? A program x has the property if x goes intoan infinite loop when fed the string x (its own encoding) as an input.• If there was a program p that recognized this property of other programs,then we could alter it so that it went into an infinite loop whenever it wouldhave answered “no.” (Just change the print “no” statement into a loop.)• Then we give this altered program p a its own program as input. If the run isinfinite, that means that the unaltered program p predicted that the answerwas “no” – p a did not go into an infinite loop on its own input. But p a justdid, so it can’t be the case that p a went into an infinite loop on itself asinput.• So p a says “yes” to its own input, which means that the original programp predicted that p a went into an infinite loop on its own input. But p a juststopped and said “yes”, so this case can’t happen either.• Other properties can be shown not to have an algorithm by proving that ifthey did, then there would be an algorithm to solve property P of programs.17