Euler's partition theorem and the combinatorics of -sequences
Euler's partition theorem and the combinatorics of -sequences Euler's partition theorem and the combinatorics of -sequences
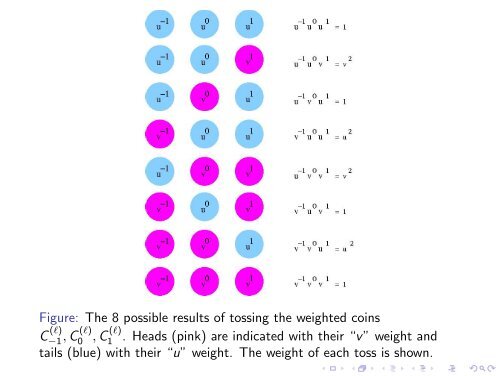
A coin-flipping interpretation of the l-nomial For real r, let C r (l) be a weighted coin for which the probability of tails is ul r /∆(l) r and the probability of heads is vl r /∆(l) r . The probability of getting exactly k heads when tossing the n coins C (l) −(n−1)/2 , C (l) 1−(n−1)/2 , C (l) 2−(n−1)/2 , . . . , C (l) (n−1)/2 : ( n k) (l) ∆ (l) −(n−1)/2 ∆(l) 1−(n−1)/2 · · · ∆(l) (n−1)/2−1 ∆(l) (n−1)/2 ∆ (l) j/2 may not be an integer, but ∆(l) −j/2 ∆(l) j/2 = ∆(l) j + 2 is.
Figure: The 8 possible results of tossing the weighted coins C (l) −1 , C (l) 0 , C (l) 1 . Heads (pink) are indicated with their “v” weight and tails (blue) with their “u” weight. The weight of each toss is shown.
- Page 5 and 6: Overview 1, 2, 3, . . . l-sequences
- Page 7 and 8: Overview 1, 2, 3, . . . l-sequences
- Page 9 and 10: Sylvester’s Bijection
- Page 11 and 12: l-sequences For integer l ≥ 2, de
- Page 13 and 14: l-sequences For integer l ≥ 2, de
- Page 15 and 16: l = 2 The l-Euler theorem [BME2]: T
- Page 17 and 18: l = 3 The l-Euler theorem [BME2]: T
- Page 19: The insertion step To insert a k +
- Page 22 and 23: Binary numeration system 1 0 1 1 0
- Page 24 and 25: Binary numeration system 1 0 1 1 0
- Page 26: Theorem [Fraenkel 1985] Every nonne
- Page 31 and 32: Lecture Hall Partitions
- Page 33 and 34: The Lecture Hall Theorem [BME1] The
- Page 35 and 36: Θ (l) n : Bijection for the l-Lect
- Page 44 and 45: Truncated lecture hall partitions L
- Page 46 and 47: Theorem [Corteel,S 2004] Given posi
- Page 48 and 49: The l-nomial coefficient Example (
- Page 50 and 51: Let u l and v l be the roots of the
- Page 52 and 53: Let u l and v l be the roots of the
- Page 54 and 55: An l-nomial theorem [LS]: An analog
- Page 58 and 59: Define a q-analog of the l-nomial:
- Page 60 and 61: Another q-analog of the l-nomial Le
- Page 62 and 63: Question: When l = 2, several refin
- Page 64 and 65: Question: What is the generating fu
- Page 66 and 67: CanaDAM 2009 2nd Canadian Discrete
Figure: The 8 possible results <strong>of</strong> tossing <strong>the</strong> weighted coins<br />
C (l)<br />
−1 , C (l)<br />
0 , C (l)<br />
1 . Heads (pink) are indicated with <strong>the</strong>ir “v” weight <strong>and</strong><br />
tails (blue) with <strong>the</strong>ir “u” weight. The weight <strong>of</strong> each toss is shown.