Chapter 3 Geometry of convex functions - Meboo Publishing ...
Chapter 3 Geometry of convex functions - Meboo Publishing ... Chapter 3 Geometry of convex functions - Meboo Publishing ...
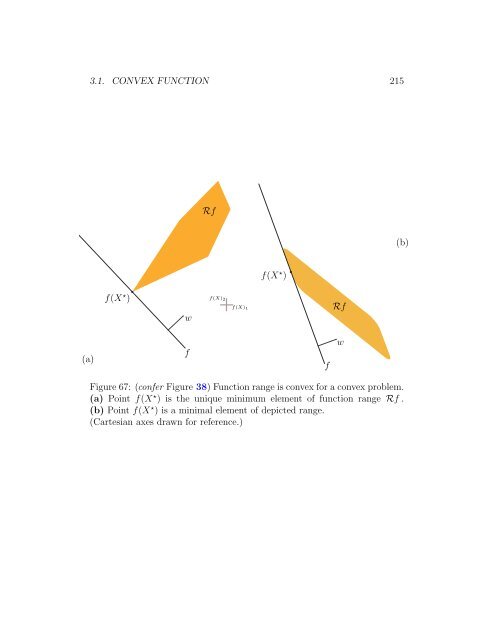
214 CHAPTER 3. GEOMETRY OF CONVEX FUNCTIONS Any convex real function f(X) has unique minimum value over any convex subset of its domain. [296, p.123] Yet solution to some convex optimization problem is, in general, not unique; e.g., given minimization of a convex real function over some convex feasible set C minimize f(X) X subject to X ∈ C any optimal solution X ⋆ comes from a convex set of optimal solutions (480) X ⋆ ∈ {X | f(X) = inf f(Y ) } ⊆ C (481) Y ∈ C But a strictly convex real function has a unique minimizer X ⋆ ; id est, for the optimal solution set in (481) to be a single point, it is sufficient (Figure 66) that f(X) be a strictly convex real 3.4 function and set C convex. [315] Quadratic real functions x T Ax + b T x + c are convex in x iff A≽0. Quadratics characterized by positive definite matrix A≻0 are strictly convex. The vector 2-norm square ‖x‖ 2 (Euclidean norm square) and Frobenius’ norm square ‖X‖ 2 F , for example, are strictly convex functions of their respective argument (each absolute norm is convex but not strictly convex). Figure 66a illustrates a strictly convex real function. 3.1.2.1 minimum/minimal element, dual cone characterization f(X ⋆ ) is the minimum element of its range if and only if, for each and every w ∈ int R M∗ + , it is the unique minimizer of w T f . (Figure 67) [59,2.6.3] If f(X ⋆ ) is a minimal element of its range, then there exists a nonzero w ∈ R M∗ + such that f(X ⋆ ) minimizes w T f . If f(X ⋆ ) minimizes w T f for some w ∈ int R M∗ + , conversely, then f(X ⋆ ) is a minimal element of its range. 3.1.2.1.1 Exercise. Cone of convex functions. Prove that relation (476) implies: the set of all vector-valued convex functions in R M is a convex cone. So, the trivial function f = 0 is convex. Indeed, any nonnegatively weighted sum of (strictly) convex functions remains (strictly) convex. 3.5 Interior to the cone are the strictly convex functions. 3.4 It is more customary to consider only a real function for the objective of a convex optimization problem because vector- or matrix-valued functions can introduce ambiguity into the optimal objective value. (2.7.2.2,3.1.2.1) Study of multidimensional objective functions is called multicriteria- [318] or multiobjective- or vector-optimization. 3.5 Strict case excludes cone’s point at origin. By these definitions (476) (479), positively weighted sums mixing convex and strictly convex real functions are not strictly convex
3.1. CONVEX FUNCTION 215 Rf (b) f(X ⋆ ) f(X ⋆ ) w f(X) 2 f(X) 1 Rf (a) f f w Figure 67: (confer Figure 38) Function range is convex for a convex problem. (a) Point f(X ⋆ ) is the unique minimum element of function range Rf . (b) Point f(X ⋆ ) is a minimal element of depicted range. (Cartesian axes drawn for reference.)
- Page 1 and 2: Chapter 3 Geometry of convex functi
- Page 3: 3.1. CONVEX FUNCTION 213 f 1 (x) f
- Page 7 and 8: 3.3. PRACTICAL NORM FUNCTIONS, ABSO
- Page 9 and 10: 3.3. PRACTICAL NORM FUNCTIONS, ABSO
- Page 11 and 12: 3.3. PRACTICAL NORM FUNCTIONS, ABSO
- Page 13 and 14: 3.3. PRACTICAL NORM FUNCTIONS, ABSO
- Page 15 and 16: 3.3. PRACTICAL NORM FUNCTIONS, ABSO
- Page 17 and 18: 3.4. INVERTED FUNCTIONS AND ROOTS 2
- Page 19 and 20: 3.5. AFFINE FUNCTION 229 3.4.1.3 po
- Page 21 and 22: 3.5. AFFINE FUNCTION 231 3.5.0.0.2
- Page 23 and 24: 3.6. EPIGRAPH, SUBLEVEL SET 233 q(x
- Page 25 and 26: 3.6. EPIGRAPH, SUBLEVEL SET 235 To
- Page 27 and 28: 3.6. EPIGRAPH, SUBLEVEL SET 237 con
- Page 29 and 30: 3.6. EPIGRAPH, SUBLEVEL SET 239 3.6
- Page 31 and 32: 3.7. GRADIENT 241 2 1.5 1 0.5 Y 2 0
- Page 33 and 34: 3.7. GRADIENT 243 From (1749) andD.
- Page 35 and 36: 3.7. GRADIENT 245 This equivalence
- Page 37 and 38: 3.7. GRADIENT 247 3.7.1.0.3 Example
- Page 39 and 40: 3.7. GRADIENT 249 f(Y ) [ ∇f(X)
- Page 41 and 42: 3.7. GRADIENT 251 meaning, the grad
- Page 43 and 44: 3.8. MATRIX-VALUED CONVEX FUNCTION
- Page 45 and 46: 3.8. MATRIX-VALUED CONVEX FUNCTION
- Page 47 and 48: 3.8. MATRIX-VALUED CONVEX FUNCTION
- Page 49 and 50: 3.9. QUASICONVEX 259 3.8.3.0.6 Exam
- Page 51 and 52: 3.9. QUASICONVEX 261 3.9.0.0.2 Defi
- Page 53: 3.10. SALIENT PROPERTIES 263 7. - N
3.1. CONVEX FUNCTION 215<br />
Rf<br />
(b)<br />
f(X ⋆ )<br />
f(X ⋆ )<br />
w<br />
f(X) 2<br />
f(X) 1<br />
Rf<br />
(a)<br />
f<br />
f<br />
w<br />
Figure 67: (confer Figure 38) Function range is <strong>convex</strong> for a <strong>convex</strong> problem.<br />
(a) Point f(X ⋆ ) is the unique minimum element <strong>of</strong> function range Rf .<br />
(b) Point f(X ⋆ ) is a minimal element <strong>of</strong> depicted range.<br />
(Cartesian axes drawn for reference.)