Test #1 Solutions - The George W. Woodruff School of Mechanical ...

George W. Woodruff School of Mechanical Engineering
Georgia Institute of Technology
ME2016A Test #1 Solutions
Summer 2007
NAME __________Key________________
______________________________________________________________________________
Problem 1 2 3 4 Total
Points /15 /15 /15 /15 /60
Please read this first:
1. The test is closed-book but you are allowed one 8 1 ×
2 11 sheet of notes.
2. There are four (4) problems in this test. Read all of the problems carefully and start from the
one that is easiest for you.
3. Budget your time -- total exam time is 1 hour and 45 minutes.
4. Make sure you have a clear presentation for the solutions. No answer without justification is
accepted.
5. Sign the pledge of honor below -- any act of academic dishonesty may result in your failing
the course.
6. Do not forget to write down your NAME.
I pledge on my honor that the work presented in this test is entirely my own; I have neither
given nor received any inappropriate aid in preparation of this test.
Signature ________________________________
STOP HERE
Do not turn the page until further instructions

-2-
ME2016 Quiz #1
NAME _____________________________
______________________________________________________________________________
Problem 1: A computer stores floating point numbers using 12-bit binary (b=2) words. Of the 10
bits, the first 2 bits are used for the signs of the exponent and mantissa, the next 4 bits are used for
the exponent, and the last 6 bits are used for the mantissa as shown below.
s 1 s 2 e 1 e 2 e 3 e 4 d 1 d 2 d 3 d 4 d 5 d 6
a) Convert the following binary floating point number to decimal for all possible values of a: (5)
0 1 0 0 1 0 a 0 0 a 0 0
fp number=(ax2 -1 +ax2 -3 )x2 -2
But since a cannot be zero (the 1 st digit of the mantissa) it has to be 1. Thus
fp number=(2 -1 +2 -3 )x2 -2 =0.140625
b) What is the largest number (in binary & decimal) that can be stored(4)
binary: 0 0 1 1 1 1 1 1 1 1 1 1
decimal: (0.111111) 2 x2 e , e=(1111) 2 =2 4 -1=15
Largest Number=(1-2 -6 )x2 15 =2 15 -2 9 =32256
c) Fill-in the blanks: Machine epsilon is the largest ___normalized_____round-off error and for
this computer it is equal to 2 -(6-1) =0.03125. (3)
d)What is the final value of E in the following script if it is run on this computer (3 pts)
E=1;
while (E+4>4)
E=E/2;
end
E=2*E;
E=4*machine-epsilon=0.125

′′′
-3-
ME2016 Quiz #1
NAME _____________________________
______________________________________________________________________________
Problem 2: The n-th order Taylor series expansion of a function f(x) about x i =1 is given by
2 3
n
h h
n h
f ( xi+ 1)
= 1−
h + − + L + ( −1)
+ Rn
2 3
n
n+
1
h
where h=x i+1 -x i is the step-size and the remainder term satisfies Rn ≤ .
n + 1
a) What are the values of the function and its first three derivatives at x i (4)
f ( x ) ______1_____, ′(
) _____ 1______, ′′
i
= f xi
= − f ( xi
) = ____1____, f ( xi
) = _____ − 2 _____
General 3 rd Taylor Series:
2
3
h h
f
3(
xi+ 1)
= f ( xi
) + f ′(
xi
) h + f ′′(
xi
) + f ′′′
( xi
)
123 123 123 2 14243 3!
1
−1
1
3
−h
/ 3
b) Approximate f(1.5) based on the third (3 rd ) order Taylor series expansion of f . Estimate the
corresponding approximation error (due to truncating the series) (6)
h=1.5-1=0.5.
2 3
0.5 0.5
f
3(1.5)
= 1−
0.5 + − ⇒ f
3
(1.5) = 0. 58333
2 3
n+
1 4
h 0.5
Max Error = Rn ≤ = ⇒ Max Error = 0. 015625
n + 1 4

-4-
ME2016 Quiz #1
NAME _____________________________
______________________________________________________________________________
c) Write a Matlab function TSA(h,emax) that computes the above Taylor series such that the
resulting approximation error (due to truncating the series) is guaranteed to be less than emax
in absolute value.(5)
function y=TSA(h,emax)
y=1;
er=emax+1;
n=1;
hn=-h;
while(er>emax)
y=y+hn/n;
hn=-hn*h;
er=abs(hn/n);
n=n+1;
end

-5-
ME2016 Quiz #1
NAME _____________________________
______________________________________________________________________________
Problem 3: We wish to find the root of f(x)=4e -x –x+0.2x 2 =0 of between 0 and 3 shown below:
4
3
2
f(x)
1
0
x
-1
-2
0 0.5 1 1.5 2 2.5 3
x
a) Use three (3) steps of the bisection algorithm to estimate the root of f(x)=0.
Approximately how many steps are needed to estimate the root to within 10 -6 of the
exact root (5 pts)
Step1: xr=(xl+xu)/2=1.5, f(xr)0⇒xl=xr=0.75
Step3: xr=(xl+xu)/2=1.125
Error≤3(1/2) n =10 -6 ⇒log3-nlog(2)=-6⇒n=22

-6-
ME2016 Quiz #1
NAME _____________________________
______________________________________________________________________________
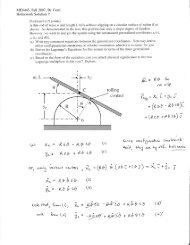
b) Use two (2) iterations of the Newton-Raphson method to find the root of f(x)=0
starting with the initial guesses of 0. Illustrate the procedure graphically. (7 pts.)
[Note: de -x /dx=-e -x ]
i x i f(x i ) f’(x i ) x i+1
0 0 4 -5 0.8
1 0.8 1.1253 -2.4773 1.2542
2 1.2542 0.2015 -1.6395 1.3772
Newton iterations:
x i+1 =x i -f(x i )/f’(x i )=x i -[(4e -x –x+0.2x 2 )/(0.4x-1-4e -x )], i=0,1,2,...
c) For what initial guesses does the Newton-Raphson have possible convergence problems
Explain what happens if you start from there graphically. (3 pts.)
For values of x 0 near 3, where f’(x 0 ) is near zero the NR algorithm may diverge

-7-
ME2016 Quiz #1
NAME _____________________________
______________________________________________________________________________
Problem 4: Consider the system of linear equations Ax=b with
⎡−1
2 0⎤
A =
⎢ ⎥
⎢
a − a 1
⎥
⎢⎣
0 a 2⎥⎦
where a is a nonzero constant.
⎡0⎤
⎥
a) Find x for and b =
⎢
⎢
1 using Gauss elimination method. You are not required to do any
⎥
⎢⎣
2⎥⎦
pivoting if not necessary. (5 pts.)
⎡−1
2 0 0⎤
⎡−1
2 0 0⎤
⎡−1
2
U :
⎢
⎥
→
⎢
⎥
→
⎢
⎢
a − a 1 1
⎥ ⎢
0 a 1 1
⎥ ⎢
0 a
⎢⎣
0 a 2 2⎥⎦
⎢⎣
0 a 2 2⎥⎦
⎢⎣
0 0
x 3 =1
ax 2 +x 3 =1⇒x 2 =0
-x 1 +2x 2 =0⇒x 1 =0
0
1
1
0⎤
1
⎥
⎥
1⎥⎦

-8-
ME2016 Quiz #1
NAME _____________________________
______________________________________________________________________________
b) Find the LU-decomposition of matrix A. You are not required to do any pivoting if not
necessary. (5 pts.)
⎡−1
2 0⎤
⎡−1
U :
⎢ ⎥ ⎢
⎢
a − a 1
⎥
→
⎢
0
⎢⎣
0 a 2⎥⎦
⎢⎣
0
⎡1
0 0⎤
⎡ 1 0
L :
⎢ ⎥
→
⎢
⎢
0 1 0
⎥ ⎢
− a 1
⎢⎣
0 1⎥⎦
⎢⎣
0
2 0⎤
⎡1
a 1
⎥ ⎢
⎥
→
⎢
0
a 2⎥⎦
⎢⎣
0
0⎤
⎡ 1
0
⎥
→
⎢
⎥ ⎢
− a
1⎥⎦
⎢⎣
0
1 0⎤
a 1
⎥
⎥
0 1⎥⎦
0 0⎤
1 0
⎥
⎥
1 1⎥⎦
c) Let A=LU be the LU-decomposition of matrix A in (b) and suppose that after performing
⎡1⎤
⎥
forward substitution we get y = Ux =
⎢
⎢
0 . Find the corresponding x and b. (4 pts.)
⎥
⎢⎣
0⎥⎦
⎡1
1 0⎤⎡x1
⎤ ⎡1⎤
Ux=
⎢ ⎥⎢
⎥ ⎢ ⎥
⎢
0 a 1
⎥⎢
x2⎥
=
⎢
0
⎥
⇒ x3
= 0, x
⎢⎣
0 0 1⎥⎦
⎢⎣
x ⎥⎦
⎢⎣
⎥
3
0⎦
⎡ 1 0 0⎤⎡1⎤
⎡ 1 ⎤
Lx=
b ⇒b
=
⎢ ⎥⎢
⎥
=
⎢ ⎥
⎢
−a
1 0
⎥⎢
0
⎥ ⎢
−a
⎥
⎢⎣
0 1 1⎥⎦
⎢⎣
0⎥⎦
⎢⎣
0 ⎥⎦
2
= 0, x
1
= 1