Exercises 1.1
Exercises 1.1
Exercises 1.1
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
•<br />
•<br />
MA111: Prepared by Dr.Archara Pacheenburawana 1<br />
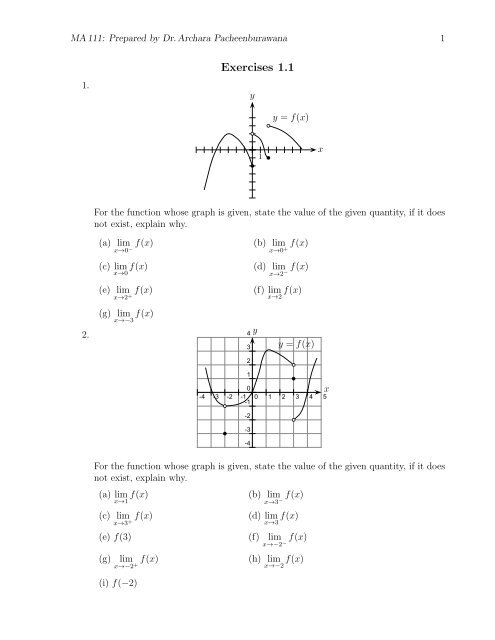
1.<br />
<strong>Exercises</strong> <strong>1.1</strong><br />
y<br />
y = f(x)<br />
1<br />
x<br />
For the function whose graph is given, state the value of the given quantity, if it does<br />
not exist, explain why.<br />
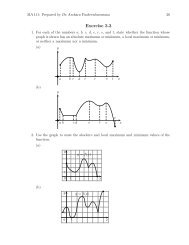
2.<br />
(a) lim<br />
x→0 −f(x)<br />
(c) lim<br />
x→0<br />
f(x)<br />
(e) lim<br />
x→2 +f(x)<br />
(g) lim<br />
x→−3 f(x)<br />
(b) lim<br />
x→0 +f(x)<br />
(d) lim<br />
x→2 −f(x)<br />
(f) lim f(x)<br />
x→2<br />
4y<br />
3<br />
2<br />
1<br />
0<br />
-4 -3 -2 -1<br />
-1<br />
0 1 2 3 4 5<br />
-2<br />
y = f(x)<br />
x<br />
-3<br />
-4<br />
For the function whose graph is given, state the value of the given quantity, if it does<br />
not exist, explain why.<br />
(a) lim<br />
x→1<br />
f(x)<br />
(c) lim<br />
x→3 +f(x)<br />
(e) f(3)<br />
(g) lim<br />
x→−2 +f(x)<br />
(i) f(−2)<br />
(b) lim<br />
x→3 −f(x)<br />
(d) lim f(x)<br />
x→3<br />
(f) lim<br />
x→−2 −f(x)<br />
(h) lim f(x)<br />
x→−2
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
MA111: Prepared by Dr.Archara Pacheenburawana 2<br />
3.<br />
4<br />
3<br />
2<br />
y<br />
y = f(x)<br />
1<br />
0<br />
-4 -3 -2 -1 0 1 2 3 4<br />
-1<br />
x<br />
For the function whose graph is given, state the value of the given quantity, if it does<br />
not exist, explain why.<br />
(a) lim<br />
x→−3 f(x)<br />
(c) f(−1)<br />
(e) f(1)<br />
(g) lim<br />
x→1 +f(x)<br />
(b) f(−3)<br />
(d) lim<br />
x→−1 f(x)<br />
(f) lim<br />
x→1 −f(x)<br />
(h) lim f(x)<br />
x→1<br />
Answer to <strong>Exercises</strong> <strong>1.1</strong><br />
1. (a) −2 (b) 2 (c) Does not exist (d) −1 (e) 3 (f) Does not exist (g) 2<br />
2. (a) 3 (b) 2 (c) −2 (d) Does not exist (e) 1 (f) −1 (g) −1 (h) −1 (i) −3<br />
3. (a) 2 (b) 1 (c) 2 (d) 5 2<br />
(e) 2 (f) 2 (g) 1 (h) Does not exist<br />
1. Given that<br />
Exercise 1.2<br />
limf(x) = −3, limg(x) = 0, lim<br />
x→a x→a<br />
h(x) = 8<br />
x→a<br />
find the limits that exist. If the limit does not exist, explain why.<br />
[ ] [ ] 2<br />
(a) lim f(x)+h(x) (b) lim f(x)<br />
x→a x→a<br />
(c) lim<br />
x→a<br />
3 √ h(x)<br />
(e) lim<br />
x→a<br />
f(x)<br />
h(x)<br />
(g) lim<br />
x→a<br />
f(x)<br />
g(x)<br />
1<br />
(d) lim<br />
x→a f(x)<br />
(f) lim<br />
x→a<br />
g(x)<br />
f(x)<br />
2f(x)<br />
(h) lim<br />
x→a h(x)−f(x)
MA111: Prepared by Dr.Archara Pacheenburawana 3<br />
2. Evaluate the following limits.<br />
(a) lim<br />
x→0<br />
(x 2 −3x+1)<br />
(c) lim<br />
x→2<br />
x−5<br />
x 2 +4<br />
√<br />
(e) lim x2 +2x+4<br />
x→1<br />
x 2 −x−12<br />
(g) lim<br />
x→−3 x+3<br />
x 2 +x−2<br />
(i) lim<br />
x→1 x 2 −3x+2<br />
(1+h) 4 −1<br />
(k) lim<br />
h→0 h<br />
t−1<br />
(m) lim √<br />
t→1 t−1<br />
t 2 +t−6<br />
(o) lim<br />
t→2 t 2 −4<br />
(q) lim<br />
x→2<br />
x 4 −16<br />
x−2<br />
(s) lim<br />
x→1<br />
[ 1<br />
x−1 − 2<br />
x 2 −1<br />
(3+h) −1 −3 −1<br />
(u) lim<br />
h→0 h<br />
√ x−x<br />
(w) lim<br />
x→1 1− √ x<br />
(y) lim<br />
x→0<br />
√ 3+x−<br />
√<br />
3<br />
x<br />
3. Evaluate lim<br />
x→2<br />
f(x) where f(x) =<br />
]<br />
(b) lim(x 3 +2)(x 2 −5x)<br />
x→3<br />
(d) lim<br />
x→1<br />
( x 4 +x 2 −6<br />
x 4 +2x+3<br />
(f) lim<br />
x→4 − √<br />
16−x<br />
2<br />
(h) lim<br />
x→−2<br />
(j) lim<br />
x→1<br />
x 3 −1<br />
x 2 −1<br />
x+2<br />
x 2 −x−6<br />
(2+h) 3 −8<br />
(l) lim<br />
h→0 h<br />
9−t<br />
(n) lim<br />
t→9 3− √ t<br />
√ √<br />
2−t− 2<br />
(p) lim<br />
t→0 t<br />
) 2<br />
x 2 −81<br />
(r) lim √<br />
x→9 x−3<br />
[<br />
1<br />
(t) lim<br />
t→0 t √ 1+t − 1 ]<br />
t<br />
x<br />
(v) lim<br />
− 1 2<br />
x−2<br />
x<br />
(x) lim √<br />
x→0 1+3x−1<br />
x→2<br />
1<br />
xe −2x+1<br />
(z) lim<br />
x→0 x 2 +1<br />
{<br />
3x 2 −2x+1 if x < 2<br />
x 3 +1 if x ≥ 2<br />
{ 2x if x < 2<br />
4. Evaluate limf(x) where f(x) =<br />
x→2 x 2 if x ≥ 2<br />
{ x<br />
5. Evaluate limf(x) where f(x) =<br />
2 +1 if x < −1<br />
x→0 3x+1 if x ≥ −1<br />
6. Evaluate lim<br />
x→−1 f(x) where f(x) = ⎧<br />
⎨<br />
⎩<br />
2x+1 if x < −1<br />
3 if −1 ≤ x < 1<br />
2x+1 if x ≥ 1<br />
7. Find the limit, if it exists. If the limit does not exist, explain why.
MA111: Prepared by Dr.Archara Pacheenburawana 4<br />
(a) lim<br />
x→−4 |x+4|<br />
2x 2 −3x<br />
(c) lim<br />
x→1.5 |2x−3|<br />
|x+4|<br />
(b) lim<br />
x→−4 − x+4<br />
( 1<br />
(d) lim<br />
x→0 + x − 1 )<br />
|x|<br />
8. Use the Squeeze Theorem to find the following limits.<br />
(a) lim<br />
x→0<br />
x 2 sin(1/x)<br />
(b) lim<br />
x→0<br />
x 2 cos(20πx)<br />
(c) lim<br />
x→0<br />
√<br />
x3 +x 2 sin π x<br />
Answer to Exercise 1.2<br />
1. (a) 5 (b) 9 (c) 2 (d) − 1 3<br />
(e) − 3 8<br />
(f) 0 (g) Does not exist (h) − 6<br />
11<br />
2. (a) 1 (b) −174 (c) − 3 8<br />
(d) 4 9<br />
(e) √ 7 (f) 0 (g) −7 (h) − 1 5<br />
(i) −3<br />
(j) 3 (k) 4 (l) 12 (m) 2 (n) 6 (o) 5 (p) − √ 2<br />
(q) 32 (r) 108 (s) 1 2 4 4 2<br />
(t) − 1 (u) − 1 (v) − 1 (w) 1 (x) 2 (y) (z) 0<br />
2 9 4 3<br />
3. 9 4. 4 5. 1 6. Does not exist 7. (a) 0 (b) −1 (c) Does not exist (d) 0<br />
8. (a) 0 (b) 0 (c) 0<br />
1−22 Evaluate the limit, if it exists.<br />
1<br />
2 √ 3<br />
Exercise 1.3<br />
1. lim<br />
x→∞<br />
x+4<br />
x 2 −2x+5<br />
−x<br />
3. lim √<br />
x→−∞ 4+x<br />
2<br />
x 3 −2x+4<br />
5. lim<br />
x→∞ 3x 2 +3x−5<br />
3x 3 −x+5<br />
7. lim<br />
x→∞ 4x 3 +4x 2 −1<br />
9. lim<br />
x→∞<br />
(√<br />
x2 +3−x<br />
11. lim<br />
x→∞<br />
1− √ x<br />
1+ √ x<br />
)<br />
13. lim<br />
x→∞<br />
(√<br />
9x2 +x−3x<br />
)<br />
(1−x)(2+x)<br />
2. lim<br />
x→−∞ (1+2x)(2−3x)<br />
x 3 −2x+1<br />
4. lim<br />
x→−∞ 3x 3 +4x−1<br />
x 2 −sinx<br />
6. lim<br />
x→∞ x 2 +4x−1<br />
x 4 −x 2 +1<br />
8. lim<br />
x→∞ x<br />
√ 5 +x 3 −x<br />
x2 +4x<br />
10. lim<br />
x→∞ 4x+1<br />
12. lim<br />
x→∞<br />
(√<br />
x2 +1− √ x 2 −1<br />
14. lim<br />
x→∞<br />
√ x<br />
)
MA111: Prepared by Dr.Archara Pacheenburawana 5<br />
15. lim<br />
x→∞<br />
(<br />
x−<br />
√ x<br />
)<br />
17. lim<br />
x→∞<br />
x 7 −1<br />
x 6 +1<br />
19. lim<br />
x→∞<br />
sin2x<br />
21. lim<br />
x→∞<br />
ln(2x)<br />
16. lim<br />
x→−∞ (x3 −5x 2 )<br />
18. lim e 2x<br />
x→∞<br />
20. lim<br />
x→∞<br />
e −3x cos2x<br />
22. lim<br />
x→0 +(xln2x)<br />
23−28 Find the horizontal asymptotes of each curve, if it exists.<br />
23. f(x) = x<br />
x+4<br />
25. f(x) = x<br />
4−x 2<br />
27. f(x) =<br />
x 3<br />
x 2 +3x−10<br />
24. f(x) =<br />
x<br />
√<br />
4+x<br />
2<br />
26. f(x) = x3<br />
4−x 2<br />
28. f(x) =<br />
x<br />
4√<br />
x4 +1<br />
Answer to Exercise 1.3<br />
1. 0 2. 1 6<br />
3. 1 4. 1 3<br />
5. ∞ 6. 1 7. 3 4<br />
8. 0 9. 0 10. 1 4<br />
11. −1 12. 0<br />
13.<br />
1<br />
6<br />
14. ∞ 15. ∞ 16. −∞ 17. ∞ 18. ∞ 19. Does not exist 20. 0<br />
21. ∞ 22. 0 23. y = 1 24. y = −1,y = 1 25. y = 0<br />
26. No horizontal asymptote 27. No horizontal asymptote 28. y = −1,y = 1<br />
1−10 Evaluate the limits.<br />
Exercise 1.4<br />
sin5x<br />
1. lim<br />
x→0 3x<br />
cosθ−1<br />
3. lim<br />
θ→0 sinθ<br />
tanx<br />
5. lim<br />
x→0<br />
7. lim<br />
x→π/4<br />
4x<br />
sinx−cosx<br />
cos2x<br />
9. lim<br />
x→0<br />
x+sinx<br />
tanx<br />
sin8t<br />
2. lim<br />
t→0 sin9t<br />
sin 2 x<br />
4. lim<br />
x→0 x<br />
cot2x<br />
6. lim<br />
x→0 cscx<br />
2xcot 2 x<br />
8. lim<br />
x→0 cscx<br />
10. lim<br />
x→0<br />
sin(cosx)<br />
secx<br />
Answer to Exercise 1.4<br />
1.<br />
5<br />
3<br />
2. 8 9<br />
3. 0 4. 0 5. 1 4<br />
6. 1 2<br />
7. − 1 √<br />
2<br />
8. 2 9. 2 10. sin1
MA111: Prepared by Dr.Archara Pacheenburawana 6<br />
Exercise 1.5<br />
1. Use the given graph to identify all discontinuility of the functions.<br />
(a)<br />
y<br />
x<br />
(b)<br />
y<br />
x<br />
(c)<br />
y<br />
x<br />
2. Use the definition of continuity and the properties of limits to show that the function<br />
is continuous at the given number.<br />
(a) f(x) = x 2 + √ 7−x, x = 4<br />
(b) g(x) = (x+2x 3 ) 4 , x = −1<br />
(c) h(x) = x+1<br />
2x 2 +1 , x = 4<br />
3. Use the definition of continuity and the properties of limits to show that the function<br />
is continuous on the given interval.<br />
(a) f(x) = 1<br />
x+1 , (−1,∞)
MA111: Prepared by Dr.Archara Pacheenburawana 7<br />
(b) f(x) = x−1<br />
x 2 −4 , (−2,2)<br />
(c) g(t) = √ 9−4t 2 , [− 3 2 , 3 2 ]<br />
(d) h(z) = √ (z −1)(3−z), [1,3]<br />
4. Explain why the function is discontinuous at the given number.<br />
(a) f(x) = x<br />
x−1 ; x = 1<br />
(b) f(x) = sin 1 x ; x = 0<br />
(c) f(x) = e 1/x ; x = 0<br />
(d) f(x) = ln|x−2|; x = 2<br />
{ 1<br />
(e) f(x) = x−1 if x ≠ 1<br />
2 if x = 1<br />
; x = 1<br />
(f) f(x) = x2 −1<br />
x+1 ; x = −1<br />
⎧<br />
⎨ x 2 −2x−8<br />
if x ≠ 4<br />
(g) f(x) =<br />
⎩<br />
x−4 ; x = 4<br />
3 if x = 4<br />
{ 1−x if x ≤ 2<br />
(h) f(x) =<br />
x 2 −2x if x > 2 ; x = 2<br />
⎧<br />
⎨ x 2 if x < 2<br />
(i) f(x) = 3 if x = 2 ; x = 2<br />
⎩<br />
3x−2 if x > 2<br />
⎧<br />
⎨<br />
(j) f(x) =<br />
⎩<br />
x 2 if x < 0<br />
−x if 0 ≤ x ≤ 1<br />
x if x > 1<br />
; x = 1<br />
5. Determine the intervals on which f(x) is continuous.<br />
(a) f(x) = 2x+ 3√ x (b) f(x) = 1<br />
x+3<br />
(c) f(x) = 1<br />
x 2 +1<br />
(e) f(x) = x2 +4<br />
x−2<br />
(g) f(x) = 3<br />
x 2 −x<br />
(i) f(x) = sinx<br />
x 2<br />
(d) f(x) = x−5<br />
|x−5|<br />
√<br />
x+1<br />
(f) f(x) = 3 x−1<br />
(h) f(x) = x<br />
4−x 2
MA111: Prepared by Dr.Archara Pacheenburawana 8<br />
6. Find the constant c that makes f(x) continuous on (−∞,∞).<br />
{ x+c if x < 0<br />
(a) f(x) =<br />
4−x 2 if x ≥ 0<br />
{ c<br />
(b) f(x) =<br />
2 −x 2 if x < 0<br />
2(x−c) 2 if x ≥ 0<br />
{<br />
cx+1 if x ≤ 3<br />
(c) f(x) =<br />
cx 2 −1 if x > 3<br />
{ x<br />
(d) f(x) =<br />
2 −c 2 if x < 4<br />
cx+20 if x ≥ 4<br />
7. Find the values a and b so that f is continuous on (−∞,∞).<br />
⎧<br />
⎨ x+1 if x < 1<br />
f(x) = ax+b if 1 ≤ x < 2<br />
⎩<br />
3x+1 if x ≥ 2<br />
8. Let<br />
Show that<br />
f(x) =<br />
{ x 2 , x ≠ 0<br />
4, x = 0<br />
and g(x) = 2x.<br />
lim f( g(x) ) ( )<br />
≠ f lim g(x) .<br />
x→0 x→0<br />
9. Use the Intermediate Value Theorem to verify that f(x) has a zero in the given<br />
interval.<br />
(a) f(x) = x 2 −7; [2,3]<br />
(b) f(x) = x 3 −4x−2; [−1,0]<br />
(c) f(x) = cosx−x; [0,1]<br />
10. Use the Intermediate Value Theorem to show that x 3 + 3x − 2 = 0 has a real root<br />
between 0 and 1.<br />
11. Use the Intermediate Value Theorem to show that (cost)t 3 + 6sin 5 t−3 = 0 has a<br />
real root between 0 and 2π.<br />
12. Show that the equation x 5 +4x 3 −7x+14 = 0 has at least one real root.<br />
Answer to Exercise 1.5<br />
1. (a) x = −2,2 (b) x = −2,1,4 (c) x = −2,2,4
MA111: Prepared by Dr.Archara Pacheenburawana 9<br />
4. (a) f(1) is not defined (b) f(0) is not defined (c) f(0) is not defined<br />
(d) f(2) is not defined (e) limf(x) is not defined (f) f(−1) is not defined<br />
x→1<br />
(g) limf(x) ≠ f(4) (h) limf(x) is not defined (i) limf(x) ≠ f(2)<br />
x→4 x→2 x→2<br />
(j) limf(x) is not defined<br />
x→1<br />
5. (a) R (b) (−∞,−3)∪(−3,∞) (c) R (d) (−∞,5)∪(5,∞) (e) (−∞,2)∪(2,∞)<br />
(f) (−∞,1)∪(1,∞) (g) (−∞,0)∪(0,1)∪(1,∞) (h) (−∞,−2)∪(−2,2)∪(2,∞)<br />
(i) (−∞,0)∪(0,∞)<br />
6. (a) 4 (b) 0 (c) 1 3<br />
(d) −2 7. a = 5, b = −3<br />
1. A curve has equation y = f(x).<br />
Exercise 2.1<br />
(a) Write an equation for the slope of the secant line through the points P ( 3,f(3) )<br />
and Q ( x,f(x) ) .<br />
(b) Write an equation for the slope of the tangent line at P.<br />
2. Suppose an object moves with position function s = f(t).<br />
(a) Write an equation for the average velocity of the object in the time interval from<br />
t = a to t = a+h.<br />
(b) Write an equation for the instantaneous velocity at time t = a.<br />
3. Find an equation of the tangent line to the curve at the given point.<br />
(a) y = x 2 −2, (1,−1)<br />
(b) y = x 2 −3x, (−2,10)<br />
(c) y = 1−2x−3x 2 , (−2,−7) (c) y = 1 x 2, (−2, 1 4 )<br />
(e) y = 2<br />
x+1 , (1,1) (f) y = √ x+3, (−2,1)<br />
4. (a) Find the slope of the tangent to the curve y = 2/(x + 3) at the point where<br />
x = a.<br />
(b) Find the slopes of the tangent lines at the points whose x-coordinates are<br />
(i) −1, (ii) 0, and (iii) 1.<br />
5. (a) Find the slope of the tangent to the curve y = x 3 − 4x + 1 at the point where<br />
x = a.<br />
(b) Find equations of the tangent lines at the point (1,−2) and (2,1).<br />
6. The following functions represent the position of an object at time t seconds. Find<br />
the average velocity between (i) t = 0 and t = 2 (ii) t = 1 and t = 2 (iii) t = 1.9<br />
and t = 2 and (iv) t = 1.99 and t = 2 and (v) estimate the instantaneous velocity<br />
at t = 2.
MA111: Prepared by Dr.Archara Pacheenburawana 10<br />
(a) s = f(t) = 16t 2 +10<br />
(b) s = f(t) = √ t 2 +8t<br />
7. Use the position function f(t) to find the velocity at time t = a.<br />
(a) f(t) = −16t 2 +5, a = 1<br />
(b) f(t) = √ t+16, a = 0<br />
8. The displacement (in meters) of the particle moving in a straight line is given by the<br />
equation of motion s = f(t) = 4t 3 +6t+2, where t is measured in seconds. Find the<br />
velocity of the particle at times t = a, t = 1, t = 2, and t = 3.<br />
1. (a) f(x)−f(3)<br />
x−3<br />
Answer to Exercise 2.1<br />
(b) lim<br />
x→3<br />
f(x)−f(3)<br />
x−3<br />
2. (a) f(a+h)−f(a)<br />
h<br />
(b) lim<br />
h→0<br />
f(a+h)−f(a)<br />
h<br />
3. (a) y = 2x−3 (b) y = −7x−4 (c) y = 10x+13 (d) y = 1 4 x+ 3 4<br />
(e) y = − 1 2 x+ 3 2<br />
(f) y = 1 2 x+2<br />
4. (a) −2/(a+3) 2 (b) (i) − 1 2<br />
(ii) − 2 9<br />
(iii) − 1 8<br />
5. (a) 3a 2 −4 (b) y = −x−1, y = 8x−15<br />
6. (a) (i) 32 (ii) 48 (iii) 62.4 (iv) 63.84 (v) 64<br />
(b) (i) 2.236 (ii) 1.472 (iii) 1.351 (iv) 1.343 (v) 1.342<br />
7. (a) −32 (b) 1 8<br />
8. 12a 2 +6, 18 m/s, 54 m/s, 114 m/s<br />
Exercise 2.2<br />
1. If f(x) = 3x 2 −5x, find f ′ (2) and use it to find an equation of the tangent line to the<br />
parabola y = 3x 2 −5x at the point (2,2).<br />
2. If g(x) = x 3 −5x+1, find g ′ (1) and use it to find an equation of the tangent line to<br />
the curve y = x 3 −5x+1 at the point (1,−3).<br />
3. Compute f ′ (a) using Definition3.2.<br />
(a) f(x) = 3x+1, a = 1 (b) f(x) = √ 3x+1, a = 1<br />
(c) f(x) = x 2 +2x, a = 0 (d) f(x) = x 3 +4, a = −1<br />
(e) f(x) = x<br />
2x−1 , a = 1 (f) f(x) = 2<br />
√ , a = −1 3−x<br />
4. Compute the derivative function f ′ (x) using Definition3.3.<br />
(a) f(x) = 3x 2 +1 (b) f(x) = 3<br />
x+1<br />
(c) f(x) = √ 3x+1<br />
(d) f(x) = x 3 +2x−1
MA111: Prepared by Dr.Archara Pacheenburawana 11<br />
5. Determine whether or not f ′ (0) exists.<br />
{ 2x+1 x < 0<br />
(a) f(x) =<br />
3x+1 x ≥ 0<br />
{<br />
xsin 1 x ≠ 0<br />
(b) f(x) = x<br />
0 x = 0<br />
Answer to Exercise 2.2<br />
1. 7, y = 7x−12 2. −2, y = −2x−1 3. (a) 3 (b) 3 4<br />
(c) 2 (d) 3 (e) −1 (f) 1 8<br />
4. (a) 6x (b)<br />
−3<br />
(x+1) 2<br />
(c)<br />
3<br />
2 √ 3x+1<br />
5. (a) Does not exist (b) Does not exist<br />
(d) 3x 2 +2<br />
Exercise 2.3<br />
1. Differentiate the function.<br />
(a) f(x) = x 3 −2x+1<br />
(b) f(x) = 3x 2 −4<br />
(c) f(x) = 4<br />
(d) f(x) = 3x 3 −2 √ x<br />
(e) f(x) = 3 −8x+1<br />
x<br />
10<br />
(f) f(x) = √ −2x x<br />
(g) f(x) = 2x 3/2 −3x −1/3 (h) f(x) = 2 3√ x+3<br />
(i) f(x) = x(3x 2 − √ x) (j) f(x) = 3x2 −3x+1<br />
2x<br />
(k) f(x) = x+ 5√ x 2 (l) f(x) = x √ x+ 1<br />
x 2√ x<br />
2. Find an equation of the tangent line to the curve at the given point.<br />
(a) y = x+ 4 x , (2,4) (b) y = x+√ x, (1,2)<br />
3. Find the points on the curve y = x 3 −x 2 −x+1 where the tangent is horizontal.<br />
4. Show that the curve y = 6x 3 +5x−3 has no tangent line with slope 4.<br />
5. Let<br />
Is f differentiable at x = 1<br />
f(x) =<br />
{<br />
2−x if x ≤ 1<br />
x 2 −2x+2 if x > 1<br />
6. For what values of x is the function f(x) = |x 2 −9| differentiable
MA111: Prepared by Dr.Archara Pacheenburawana 12<br />
7. For what values of a and b is the line 2x + y = b tangent to the parabola y = ax 2<br />
when x = 2<br />
8. Find a cubic function y = ax 3 +bx 2 +cx+d whose graph has horizontal tangents at<br />
the points (−2,6) and (2,0).<br />
9. Differentiate.<br />
(a) f(x) = (x 2 +3)(x 3 −3x+1)<br />
(b) f(x) = (3x+4)(x 3 −2x 2 +x)<br />
(c) f(x) = ( √ (<br />
x+3x) 5x 2 − 3 )<br />
x<br />
(d) f(x) = 3x−2<br />
5x+1<br />
(f) f(x) = 3x−6√ x<br />
5x 2 −2<br />
(h) f(x) = x2 +3x−2<br />
√ x<br />
(j) f(x) = (x 2 +1) x3 +3x 2<br />
x 2 +2<br />
(e) f(x) = x−2<br />
x 2 +x+1<br />
(g) f(x) = (x+1)(x−2)<br />
x 2 −5x+1<br />
(i) f(x) = x( 3√ x+3)<br />
(k) f(x) = x<br />
x+ c x<br />
10. Find an equation of the tangent line to the curve at the given point.<br />
(a) y = 2x<br />
1<br />
, (1,1) (b) y =<br />
x+1 1+x , (−1, 1)<br />
2 2<br />
11. Write put the product rule for the function f(x)g(x)h(x).<br />
12. Find the derivative of each function using the general product rule developed in exercise<br />
12.<br />
(a) f(x) = x 2/3 (x 2 −2)(x 3 −x+1)<br />
(b) f(x) = (x+1)(x 3 +4x)(x 5 −3x 2 +1)<br />
13. If f and g are the functions whose graphs are shown, let u(x) = f(x)g(x) and v(x) =<br />
f(x)/g(x).<br />
(a) Find u ′ (1). (b) Find v ′ (1).<br />
y<br />
1<br />
f<br />
g<br />
1<br />
x
MA111: Prepared by Dr.Archara Pacheenburawana 13<br />
14. Suppose that f(5) = 1, f ′ (5) = 6, g(5) = −3, and g ′ (5) = 2. Find the values of (a)<br />
(fg) ′ (5), (b) (f/g) ′ (5), and (c) (g/f) ′ (5).<br />
Answer to Exercise 2.3<br />
1. (a) 3x 2 −2 (b) 6x (c) 0 (d) 9x 2 − 1 √ x<br />
(e) − 3<br />
x 2 −8 (f) −5x −3/2 −2<br />
(g) 3x 1/2 +x −4/3 (h) 2 3 x−2/3 (i) 9x 2 − 3 2 x1/2 (j) 3 2 − 1 2 x−2 (k) 1+2/(5 5√ x 3 )<br />
(l) 3 2√ x−5/(2x<br />
3 √ x)<br />
2. (a) y = 4 (b) y = 3x+ 1 3. (1,0),(− 1, 32 ) 5. No<br />
2 2 3 27<br />
6. Not differentiable at x = −3 or 3 7. a = − 1 3<br />
,b = 2 8. y =<br />
2 16 x3 − 9 x+3 4<br />
9. (a) 2x(x 3 −3x+1)+(x 2 +3)(3x 2 −3) (b) 3(x 3 −2x 2 +x)+(3x+4)(3x 2 −4x+1)<br />
( )( 1<br />
(c)<br />
2 x−1/2 +3 5x 2 − 3 )<br />
+( √ x+3x)(10x+3x −2 13<br />
) (d)<br />
x<br />
(5x+1) 2<br />
(e) −x2 +4x+3<br />
(f) (3−3x−1/2 )(5x 2 −2)−(3x−6 √ x)(10x)<br />
(x 2 +x+1) 2 (5x−2) 2<br />
(h) 3 2 x1/2 + 3 2 x−1/2 +x −3/2 (i) 4 3 x1/3 +3<br />
(j) 2x x3 +3x 2<br />
x 2 +2 +(x2 −1) (3x2 +6x)(x 2 +2)−(x 3 +3x 2 )(2x)<br />
(x 2 +2) 2 (k)<br />
(g) −4x2 +6x−11<br />
(x 2 −5x+1) 2<br />
2cx<br />
(x 2 +c) 2<br />
10. (a) y = 1 2 x+ 1 2<br />
(b) y = 1 2 x+1 11. f′ (x)g(x)h(x)+f(x)g ′ (x)h(x)+f(x)g(x)h ′ (x)<br />
12. (a) 2 3 x−1/3 (x 2 −2)(x 3 −x+1)+2x 4/3 (x 3 −x+1)+x 2/3 (x 2 −2)(3x 2 −1)<br />
(b) (x 3 +4x)(x 5 −3x 2 +1)+(x+1)(3x 2 +4)(x 5 −3x 2 +1)+(x+1)(x 3 +4x)(5x 4 −6x)<br />
13. (a) 0 (b) − 2 3<br />
14. (a) −6 (b) − 20 9<br />
(c) 20<br />
1. Find the derivative of each function.<br />
(a) f(x) = 4sinx−x<br />
Exercise 2.4<br />
(c) f(x) = xcosx<br />
(e) f(x) = sinx<br />
x<br />
(g) f(x) = cosx−1 (h) f(x) =<br />
x 2<br />
(i) f(x) = cscxcotx<br />
(k) f(x) = 2sinxcosx<br />
(m) f(x) = 4sin 2 x+4cos 2 x<br />
(b) f(x) = tanx−cscx<br />
(d) f(x) = 4 √ x−2sinx<br />
(f) f(x) = tanx<br />
x<br />
x<br />
sinx+cosx<br />
(j) f(x) = sinxsecx<br />
(l) f(x) = 4x 2 tanx
MA111: Prepared by Dr.Archara Pacheenburawana 14<br />
2. Prove, using the definition of derivative, that if f(x) = cosx, then f ′ (x) = −sinx.<br />
3. Find an equation of the tangent line to the given curve at the specified point.<br />
(a) y = sinx, ( π 2 ,1) (b) y = cosx, (π 2 ,0)<br />
(c) y = tanx, ( π ,1) (d) y = x+cosx, (0,1)<br />
4<br />
(e) y = xcosx, (π,−π) (f) y = 3tanx−2cscx at x = π 3<br />
4. For what values of x does the graph of f(x) = x+2sinx have a horizontal tangent.<br />
5. Using the identities sin2x = 2sinxcosx and cos2x = cos 2 x − sin 2 x, prove that if<br />
f(x) = sin2x, then f ′ (x) = 2cos2x.<br />
6. Using the identities sin2x = 2sinxcosx and cos2x = cos 2 x − sin 2 x, prove that if<br />
f(x) = cos2x, then f ′ (x) = −2sin2x.<br />
Answer to Exercise 2.4<br />
1. (a) 4cosx−1 (b) sec 2 x+cscxcotx (c) cosx−xsinx (d) 2x −1/2 −2cosx<br />
(e) xcosx−sinx<br />
x 2<br />
(f) xsec2 x−tanx<br />
x<br />
(g) −x2 sinx−(cosx−1)2x<br />
x 4<br />
(h) sinx+cosx+xsinx−xcosx (i) −cscxcot 2 x−csc 3 x (j) sec 2 x<br />
1+sin2x<br />
(k) 2cos 2 x−2sin 2 x (l) 8xtanx+4x 2 sec 2 x (m) 0<br />
3. (a) y = 1 (b) y = −x+ π (c) y = 2x+1− π (d) y = x+1 (e) y = −x<br />
2 2<br />
( √<br />
(f) y = 40 3 x−<br />
π<br />
3)<br />
+3 3− √3 4<br />
4. (2n+1)π ±π/3, n an integer<br />
1. Find the derivative of each function.<br />
Exercise 2.5<br />
(a) f(x) = (x 3 +4x) 7 (b) f(x) = (x 3 +x−1) 3<br />
(c) f(x) = √ x 2 −7x (d) f(x) = √ x 2 +4<br />
(<br />
(e) f(x) = x−<br />
x) 1 3/2<br />
(f) f(x) = sin(2x 2 +3)<br />
(g) f(x) = cos(a 3 +x 3 )<br />
(h) f(x) = tan 2 x<br />
(i) f(x) = (3x−2) 10 (5x 2 −x+1) 12 (i) f(x) = (2x−5) 4 (8x 2 −5)<br />
( ) −3<br />
3 x−6<br />
1<br />
(k) f(x) =<br />
(l) f(x) =<br />
x+7<br />
5√ 2x−1
MA111: Prepared by Dr.Archara Pacheenburawana 15<br />
(m) f(x) = tan(cosx)<br />
(o) f(x) = sec 3 4x<br />
(<br />
(q) f(x) = sin tan √ )<br />
sinx<br />
(n) f(x) = x 2 sin4x<br />
(p) f(x) = √ x+ √ x<br />
2. Find an equation of the tangent line to y = f(x) at x = a.<br />
(a) y = √ 8<br />
x 2 +16, a = 3 (b) y = √ , a = 4 4+3x<br />
(c) y = sin(sinx), a = π (d) y =<br />
2<br />
1+e −x , a = 0<br />
3. Findall pointsonthegraphofthefunctionf(x) = 2sinx+sin 2 xatwhich thetangent<br />
line is horizontal.<br />
4. Suppose that F(x) = f ( g(x) ) and g(3) = 6, g ′ (3) = 4, f ′ (3) = 2, and f ′ (6) = 7. Find<br />
F ′ (3).<br />
5. If f and g are the functions whose graphs are shown, let u(x) = f ( g(x) ) , v(x) =<br />
g ( f(x) ) , and w(x) = g ( g(x) ) . Find each derivative, if it exists. If it dose not exist,<br />
explain why.<br />
(a) u ′ (1) (b) v ′ (1) (c) w ′ (1)<br />
y<br />
f<br />
1<br />
g<br />
1<br />
x<br />
6. A table of values for f, g, f ′ , and g ′ is given.<br />
(a) If h(x) = f ( g(x) ) , find h ′ (1).<br />
(b) If H(x) = g ( f(x) ) , find H ′ (1).<br />
x f(x) g(x) f ′ (x) g ′ (x)<br />
1 3 2 4 6<br />
2 1 8 5 7<br />
3 7 2 7 9
MA111: Prepared by Dr.Archara Pacheenburawana 16<br />
Answer to Exercise 2.5<br />
1. (a) 7(x 3 +4x) 6 (3x 2 +4) (b) 3(3x 2 +1)(x 3 +x−1) 2 (c)<br />
2x−7<br />
2 √ x 2 −7x<br />
(d) x(x 2 +4) −1/2 (e) 3 2 (x−1/x)1/2 (1+1/x 2 ) (f) 4xcos(2x 2 +3)<br />
(g) −3x 2 sin(a 3 +x 3 ) (h) 2tanxsec 2 x (i) 6(3x−2) 9 (5x 2 −x+1) 11 (85x 2 −51x+9)<br />
(j) 8(2x−5) 3 (8x 2 −5) −4 (−4x 2 +30x−5) (k) 39(x−6)2<br />
(x+7) 4<br />
(l) − 2 5 (2x−1)−6/5<br />
(m) −sinxsec 2 (cosx) (n) 2xsin4x+4x 2 cos4x (o) 12sec 3 4xtan4x<br />
(p) [1+1/(2 √ x)]/(2 √ x+ √ x)<br />
(q) cos ( tan √ sinx ) (sec 2√ sinx) [ 1/(2 √ sinx) ] (cosx)<br />
2. (a) y = 3 16<br />
x+ (b) y = − 3 11<br />
x+ (c) y = −x+π (d) y = 1x+1<br />
5 5 16 4 2<br />
3. ( π<br />
2 +2nπ,3) , ( 3π<br />
2 +2nπ,−1) ,n an integer 4. 28<br />
5. (a) 3 4<br />
(b) Does not exist (c) −2 6. (a) 30 (b) 36<br />
1. Find the derivative y ′ (x) implicitly.<br />
Exercise 2.6<br />
(a) x 2 +y 2 = 1 (b) x 3 +x 2 y +4y 2 = 6<br />
(c) x 2 y +xy 2 = 3x (d) x 2 y 2 +3y = 4x<br />
(e) √ xy −4y 2 = 12 (f) x+3 = 4x+y 2<br />
y<br />
(g) √ x+y −4x 2 y<br />
= y (h)<br />
x−y = x2 +1<br />
(i) √ xy = 1+xy (j) 4cosxsiny = 1<br />
(k) xy = cot(xy)<br />
2. Find an equation of the tangent line to the curve at the given point.<br />
(a) x 2 −4y 2 = 0, (2,1) (b) x 2 −4y 3 = 0, (2,1)<br />
(c) x 2 y 2 = 4y, (2,1) (d) x 3 y 3 = 9y, (1,3)<br />
(e) x2<br />
16 − y2<br />
9 = 1, (−5, 9 4 ) (f) y2 = x 3 (2−x), (1,1)<br />
(g) 2(x 2 +y 2 ) 2 = 25(x 2 −y 2 ), (3,1) (h) y 2 = x 3 +3x 2 , (1,2)<br />
(i) y(y 2 −1)(y −2) = x(x−1)(x−2), (0,1)
MA111: Prepared by Dr.Archara Pacheenburawana 17<br />
3. Find an equation of the tangent line to the hyperbola<br />
at the point (x 0 ,y 0 ).<br />
x 2<br />
a 2 − y2<br />
b 2 = 1<br />
4. Find all points on the curve x 2 y 2 +xy = 2 where the slope of the tangent line is −1.<br />
5. If x [ f(x) ] 3<br />
+xf(x) = 6 and f(3) = 1, then find f ′ (3).<br />
1. (a) −x<br />
y<br />
(f)<br />
y −4y 2<br />
x+3+2y 3<br />
(j) tanxtany<br />
(b) −x(3x+2y)<br />
x 2 +8y<br />
Answer to Exercise 2.6<br />
(c)<br />
(g) 16x√ x+y −1<br />
1−2 √ x+y<br />
(k) −y<br />
x<br />
3−2xy −y2<br />
x 2 +2xy<br />
(d) 4−2xy2<br />
3+2x 2 y<br />
(h) 2x(x−y)2 +y<br />
x<br />
(e)<br />
y<br />
16y √ xy −x<br />
(i) 2y√ xy −y<br />
x−2x √ xy<br />
2. (a) y = 1 2 x (b) y = 1 3 x+ 1 3<br />
(c) y = −x+3 (d) y = − 9 2 x+ 15 2<br />
(e) y = − 5 4 x−4<br />
3.<br />
(f) y = x (g) y = − 9 40<br />
x+ (h) y = 9 x− 5 (i) y = −x+1<br />
13 13 2 2<br />
x 0 x<br />
a − y 0y<br />
= 1 4. (−1,−1),(1,1) 5. − 1 2 b 2 6<br />
Exercise 2.7<br />
Find the derivative of each function.<br />
1. y = sin −1 (x 2 ) 2. y = tan −1 (e x )<br />
3. y = cos −1 (x 3 ) 4. y = sec −1 (x 2 )<br />
5. H(x) = (1+x 2 )tan −1 x 6. g(t) = sin −1 (4/t)<br />
7. y = x 2 cot −1 (3x) 8. f(x) = e x −x 2 tan −1 x<br />
9. y = tan −1 (cos2x) 10. y = xcos −1 (2x)<br />
11. y = cos −1 (sinx) 12. y = tan −1 (secx)<br />
Answer to Exercise 2.7<br />
1.<br />
2x<br />
√<br />
1−x<br />
4<br />
2.<br />
e x<br />
1+e 2x 3.<br />
−3x 2<br />
√<br />
1−x<br />
6<br />
4.<br />
2<br />
x √ x 4 −1<br />
7. 2xcot −1 (3x)− 3x2<br />
1+9x 2 8. e x − x2<br />
1+x 2 −2xtan−1 x 9.<br />
10. cos −1 2x−<br />
2x<br />
√<br />
1−4x<br />
2<br />
11.<br />
−cosx<br />
√<br />
1−sin 2 x<br />
= ±1 12.<br />
secxtanx<br />
1+sec 2 x<br />
5. 1+2xtan −1 x 6.<br />
−2sin2x<br />
1+cos 2 2x<br />
−4<br />
√<br />
t4 −16t 2
MA111: Prepared by Dr.Archara Pacheenburawana 18<br />
Exercise 2.8<br />
1. Find the derivative of each function.<br />
(a) f(x) = 4e x −x<br />
(b) f(x) = xe x<br />
(c) f(x) = x−2 x (d) f(x) = 2e x+1<br />
(e) f(x) = (1/3) x<br />
(f) f(x) = 4 −x+1<br />
(g) f(x) = e 2x<br />
(i) f(x) = ex<br />
x<br />
2. Differentiate the function.<br />
(h) f(x) = x 2 e −x<br />
(a) f(x) = ln(2x) (b) f(x) = ln(x 3 )<br />
(c) f(θ) = ln(cosθ) (d) f(x) = log 3 (x 2 −4)<br />
(e) f(x) = ln √ x<br />
( ) a−x<br />
(g) f(x) = ln<br />
a+x<br />
(i) f(x) = lnx<br />
1+x<br />
(f) f(x) = √ xlnx<br />
(h) f(x) = e x lnx<br />
(j) f(x) = |x 3 −x 2 |<br />
(k) f(x) = ln(e −x +xe −x ) (l) f(x) = x 2 ln(1−x 2 )<br />
3. Find an equation of the tangent line to the curve at the given point.<br />
(a) y = x 2 lnx, (1,0)<br />
(b) y = ln(lnx), (e,0)<br />
4. Use logarithmic differentiation to find the derivative of the function.<br />
(a) y = (2x+1) 5 (x 4 −3) 6 (b) y = sin2 xtan 4 x<br />
(x 2 +1) 2<br />
(c) y = x x<br />
(d) y = x sinx<br />
(e) y = (lnx) x<br />
(f) y = x ex<br />
Answer to Exercise 2.8<br />
1. (a) 4e x −1 (b) e x +xe x (c) 1+(ln2)2 x (d) 2e x+1 (e) ( ln 3)( 1 1<br />
3<br />
(f) −(ln4)4 −x+1 (g) 2e 2x (h) 2xe −x −x 2 e −x (i) xex −e x<br />
2. (a) f ′ (x) = 1 x (b) f′ (x) = 3 x (c) f′ (θ) = −tanθ (d) f ′ (x) =<br />
(e) f ′ (x) = 1<br />
2x (f) f′ (x) = 2+lnx<br />
2 √ x<br />
x 2<br />
(g) f ′ (x) = −2a<br />
a 2 −x 2<br />
) x<br />
2x<br />
(x 2 −4)ln3
MA111: Prepared by Dr.Archara Pacheenburawana 19<br />
(<br />
(h) f ′ (x) = e x lnx+ 1 )<br />
x<br />
(i) f ′ (x) = 1+x−xlnx<br />
x(1+x) 2<br />
(k) f ′ (x) = −x<br />
1+x (l) f′ (x) = 2xln(1−x 2 )− 2x3<br />
1−x 2<br />
(j) f ′ (x) = 3x−2<br />
x(x−1)<br />
( 10<br />
3. (a) y = x−1 (b) x−ey = e 4. (a) y ′ = (2x+1) 5 (x 4 −3) 6 2x+1 + 24x3<br />
x 4 −3<br />
(<br />
(b) y ′ = sin2 xtan 4 x<br />
2cotx+ 4sec2 x<br />
(x 2 +1) 2 tanx − 4x )<br />
(c) y ′ = x x (lnx+1)<br />
x 2 +1<br />
[<br />
(d) y ′ = x sinx cosxlnx+ sinx<br />
x<br />
(<br />
(f) y ′ = e x x ex lnx+ 1 )<br />
x<br />
]<br />
(e) y ′ = (lnx) x (<br />
lnlnx+ 1<br />
lnx<br />
)<br />
)<br />
Differentiate the function.<br />
1. f(x) = xcoshx+sinh(x 2 )<br />
2. g(x) = 1−coshx<br />
1+coshx<br />
3. h(x) = coth √ 1+x 2 −tanh(e x )<br />
4. y = e cosh3x +tanh −1√ x<br />
5. f(x) = xsinh −1 (x/3)− √ 9+x 2<br />
6. g(x) = coth −1√ x 2 +1<br />
Exercise 2.9<br />
Answer to Exercise 2.9<br />
1. f ′ (x) = xsinhx+coshx+2xcosh(x 2 ) 2. g ′ (x) = −2sinhx<br />
(1+coshx) 2<br />
3. h ′ (x) = −x·csch 2√ 1+x 2<br />
√<br />
1+x<br />
2<br />
5. f ′ (x) = sinh −1 (x/3) 6. g ′ −1<br />
(x) =<br />
x √ x 2 +1<br />
+e x sech 2 (e x ) 4. y ′ = 3e cosh3x sinhx+<br />
1<br />
2 √ x(1−x)
MA111: Prepared by Dr.Archara Pacheenburawana 20<br />
Exercise 2.10<br />
1. Find the first and second derivatives of the function.<br />
(a) f(x) = x 4 +3x 2 −2 (b) f(x) = x 5 +6x 2 −7x<br />
(c) f(x) = x 6 + √ x (d) f(x) = √ 2x+1<br />
(e) f(x) = e 2x<br />
(f) y = cos2θ<br />
(g) h(x) = √ x 2 +1 (h) F(s) = (3s+5) 8<br />
(i) y = x<br />
1−x<br />
(k) H(t) = tan3t<br />
(j) y = (1−x 2 ) 3/4<br />
(l) g(t) = t 3 e 5t<br />
2. If f(x) = (2−3x) −1/2 , find f(0), f ′ (0), f ′′ (0), and f ′′′ (0).<br />
3. If f(θ) = cotθ, find f ′′′ (π/6).<br />
4. Find a formula for f (n) (x).<br />
(a) f(x) = 1 x<br />
(b) f(x) = e 2x (c) f(x) = 1<br />
3x 3<br />
5. Find a second-degree polynomial P such that P(2) = 5, P ′ (2) = 3, and P ′′ (2) = 2.<br />
6. For what values of r does the function y = e rx satisfy the equation y ′′ +5y ′ −6y = 0<br />
1. (a) f ′ (x) = 4x 3 +6x, f ′′ (x) = 12x 2 +6<br />
2.<br />
Answer to Exercise 2.10<br />
(b) f ′ (x) = 5x 4 +12x−7, f ′′ (x) = 20x 3 +12<br />
(c) f ′ (x) = 6x 5 + 1 2 x−1/2 , f ′′ (x) = 30x 4 − 1 4 x−3/2<br />
(d) f ′ (x) = (2x+1) −1/2 , f ′′ (x) = −(2x+1) −3/2<br />
(e) f ′ (x) = 2e 2x , f ′′ (x) = 4e 2x (f) y ′ = −2sin2θ, y ′′ = −4cos2θ<br />
(g) h ′ x<br />
(x) = √<br />
x2 +1 , 1<br />
f′′ (x) =<br />
(x 2 +1) 3/2<br />
(h) F ′ (s) = 24(3s+5) 7 , F ′′ (s) = 504(3s+5) 6 (i) y ′ =<br />
(j) y ′ = − 3 2 x(1−x2 ) −1/4 , y ′′ = 3 4 (1−x2 ) −5/4 (x 2 −2)<br />
(k) H ′ (t) = 3sec 2 3t, H ′′ (t) = 18sec 2 3ttan3t<br />
(l) g ′ (t) = t 2 e 5t (5t+3), g ′′ (t) = te 5t (25t 2 +30t+6)<br />
1<br />
√<br />
2<br />
,<br />
3<br />
4 √ 2 , 27<br />
16 √ 2 , 405<br />
64 √ 2<br />
5. P(x) = x 2 −x+3 6. r = 1,−6<br />
3. −80 4. (a) (−1)n n!<br />
x n+1<br />
1<br />
(1−x) 2, y′′ =<br />
2<br />
(1−x) 3<br />
(b) 2 n e 2x (c) (−1)n (n+2)!<br />
6x n+3
MA111: Prepared by Dr.Archara Pacheenburawana 21<br />
Exercise 2.11<br />
1. Find the linearization L(x) of the function at a.<br />
(a) f(x) = x 3 , a = 1 (b) f(x) = lnx, a = 1<br />
(c) f(x) = e −2x , a = 0<br />
2. Find the differential of the function.<br />
(d) f(x) = 3√ x, a = −8<br />
(a) y = x 2 +x−3 (b) y = x 4 +5x<br />
(c) y = (2x+3) −4 (d) y = xlnx<br />
(e) y = (sinx+cosx) 3 (f) y = x+1<br />
x−1<br />
(g) y = (7x 2 +3x−1) −3/2 (h) y = 5√ (x−2) 2<br />
3. Use a linear approximation to estimate the given number.<br />
(a) √ 402 (b) √ 35.9<br />
(c) √ 36.1 (d) 3√ 1.02+ 4√ 1.02<br />
1<br />
(e)<br />
10.1<br />
(f) sin59 ◦<br />
1<br />
(g) 3√<br />
9<br />
(h) 3√ 8.01− 3√ 1<br />
8.01<br />
Answer to Exercise 2.11<br />
1. (a) L(x) = 3x−2 (b) L(x) = x−1 (c) L(x) = 1−2x (d) L(x) = 1<br />
12 x− 4 3<br />
2. (a) dy = (2x+1)dx (b) dy = (4x 3 +5)dx (c) dy = −8(2x+3) −5 dx<br />
(d) dy = (1+lnx)dx (e) dy = 3(sinx+cosx) 2 (cosx−sinx)dx<br />
(f) dy = −2/(x−1) 2 dx (g) dy = − 3 2 (7x2 +3x−1) −5/2 (14x+3)dx<br />
(h) dy =<br />
2<br />
5 5√ (x−2) 3 dx<br />
3. (a) 20.05 (b) 5.9917 (c) 6.0083 (d) 2.0117 (e) 0.099 (f) 0.857 (g) 0.479<br />
(h) 1.501<br />
Exercise 4.1<br />
1. If A is the area of a circle with radius r and the circle expands as time passed, find<br />
dA/dt in terms of dr/dt.<br />
2. If V is the volume of a cube with edge length x and the cube expands as time passed,<br />
find dV/dt in terms of dx/dt.
MA111: Prepared by Dr.Archara Pacheenburawana 22<br />
3. Aplaneflying horizontallyatthealtitude1mi andaspeed of500mi/hpassed directly<br />
over a radar station. Find the rate at which the distance from the plane to the station<br />
is increasing when it is 2 mi away from the station.<br />
4. A street light is mounted at the top of a 15-ft-tall pole. A men 6 ft tall walks away<br />
from the pole with a speed of 5 ft/s along a straight path. How fast is the tip of his<br />
shadow moving when he is 40 ft from the pole<br />
5. A man starts walking north at 4 ft/s from a point P. Five minutes later a woman<br />
starts walking south at 5 ft/s from a point 500 ft due east to P. At what rate are the<br />
people moving apart 15 min after the women starts walking<br />
6. The altitude of a triangle is increasing at a rate of 1 cm/min while the area of the<br />
triangle is increasing at a rate of 2 cm 2 /min. At what rate is the base of the triangle<br />
changing when the altitude is 10 cm and the area is 100 cm 2 <br />
7. At noon, ship A is 100 km west of ship B. Ship A is sailing south at 35 km/h and ship<br />
B is sailing north at 25 km/h. How fast is the distance between the ships changing<br />
at 4:00pm.<br />
8. Two sides of a triangle are 4 m and 5 m in length and the angle between them is<br />
increasing at a rate 0.06 rad/s. Find the rate at which the area of the triangle is<br />
increasing when the angle between the sides of fixed length is π/3.<br />
9. A plane flying with a constant speed of 300 km/h passes over a ground radar station<br />
at an altitude of 1 km and climbs at an angle 30 ◦ . At what rate is the distance from<br />
the plane to the radar station increasing a minute later<br />
10. Water is leaking out of an inverted conical tank at a rate of 10,000 cm 3 /min at the<br />
same time that water is being pumped into the tank at a constant rate. The tank has<br />
height 6 m and the diameter at the top is 4 m. If the water level is rising at a rate<br />
20 cm/min when the height of the water is 2 m, find the rate at which water is being<br />
pumped into the tank.<br />
11. A kite 100 ft above the ground moves horizontally at a speed of 8 ft/s. At what rate<br />
is the angle between the string and the horizontal decreasing when 200 ft of string<br />
have been let out<br />
12. Boyle’s Lawstatesthatwhenasample ofgasiscompressed ataconstant temperature,<br />
the pressure P and volume V satisfy the equation PV = C, where C is a constant.<br />
Suppose that at a certain instant the volume is 600 cm 3 , the pressure is 150 kPa,<br />
and the pressure is increasing at a rate of 20 kPa/min. At what rate is the volume<br />
decreasing at this instant<br />
13. Suppose that the average yearly cost per item for producing x items of a business<br />
product is C(x) = 10 + 100 . If the current production is x = 10 and production is<br />
x<br />
increasing at a rate of 2 items per year, find the rate of change of the average cost.
MA111: Prepared by Dr.Archara Pacheenburawana 23<br />
1.<br />
dA<br />
dt<br />
= 2πr<br />
dr<br />
dt<br />
2. dV<br />
dt = 3x2dx dt<br />
Answer to Exercise 4.1<br />
3. 250 √ 3 mi/h 4. 25<br />
3 ft/s<br />
5. 837/ √ 8674 ≈ 8.99 ft/s 6. −1.6 cm/min 7. 720<br />
13 ≈ 55.4 km/h 8. 0.3 m2 /s<br />
9. 1650/ √ 31 ≈ 296 km/h 10. ≈ 2.79×10 5 cm 3 /min 11. 2 √ 3 ft/s<br />
12. 80 cm 3 /min 13. −2 dollars per year<br />
Exercise 4.2<br />
Find the following limit.<br />
x+2<br />
1. lim<br />
x→−2 x 2 −4<br />
3x 2 +2<br />
3. lim<br />
x→∞ x 2 −4<br />
e x −1<br />
5. lim<br />
x→0 sinx<br />
sinx−x<br />
7. lim<br />
x→0 x 3<br />
x 3<br />
9. lim<br />
x→∞ e x<br />
11. lim<br />
x→1<br />
sinπx<br />
x−1<br />
13. lim<br />
x→∞<br />
xe −x<br />
15. lim<br />
x→0 +xlnx<br />
(√ )<br />
17. lim x2 −1−x<br />
x→∞<br />
19. lim<br />
(lnx+ 1 )<br />
x→0 + x<br />
21. lim<br />
x→0 +xsinx<br />
2. lim<br />
x→−2<br />
x+1<br />
x 2 +4x+3<br />
x+1<br />
4. lim<br />
x→−∞ x 2 +4x+3<br />
sinx<br />
6. lim<br />
x→0 x 3<br />
√ x−1<br />
8. lim<br />
x→1 x−1<br />
e x −1<br />
10. lim<br />
x→0 x<br />
lnx<br />
12. lim<br />
x→∞ x 2<br />
xsinx<br />
14. lim<br />
x→0 cosx−1<br />
lnx<br />
16. lim<br />
x→0 + cotx<br />
18. lim<br />
x→∞<br />
(1+ 1 x<br />
20. lim<br />
x→0 +(1/x)x<br />
) x<br />
22. lim<br />
x→0<br />
(1−2x) 1/x<br />
Answer to Exercise 4.2<br />
1. − 1 4<br />
2. 1 3. 3 4. 0 5. 1 6. ∞ 7. − 1 6<br />
8. 1 2<br />
9. 0 10. 1 11. −π<br />
12. 0 13. 0 14. −2 15. 0 16. 0 17. 0 18. e 19. ∞ 20. 1 21. 1 22. e −2