Exercise 3.3
Exercise 3.3
Exercise 3.3
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
MA111: Prepared by Dr.Archara Pacheenburawana 26<br />
<strong>Exercise</strong> <strong>3.3</strong><br />
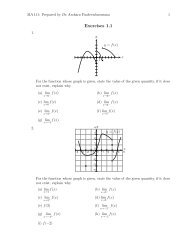
1. For each of the numbers a, b, c, d, e, r, s, and t, state whether the function whose<br />
graphisshown hasanabsolutemaximum orminimum, a localmaximum orminimum,<br />
or neither a maximum nor a minimum.<br />
(a)<br />
y<br />
a b c d e r s t<br />
x<br />
(b)<br />
y<br />
a b c d e r s<br />
t<br />
x<br />
2. Use the graph to state the absolute and local maximum and minimum values of the<br />
function.<br />
(a)<br />
y<br />
y = f(x)<br />
1<br />
0<br />
1<br />
x<br />
(b)<br />
y<br />
y = f(x)<br />
1<br />
0<br />
1<br />
x
MA111: Prepared by Dr.Archara Pacheenburawana 27<br />
3. Find all critical numbers and the local extreme values of the following functions.<br />
(a) f(x) = x 2 +5x−1<br />
(b) f(x) = x 3 −3x+1<br />
(c) f(x) = x 3 −3x 2 +3x (d) f(x) = x 4 −3x 3 +2<br />
(e) f(x) = x 3/4 −4x 1/4 (f) f(x) = x 3 −2x 2 −4x<br />
(g) f(x) = sinxcosx, [0,2π] (h) f(x) = x+1<br />
x−1<br />
(i) f(x) = x (j) f(x) = 1<br />
x 2 2<br />
+1<br />
(ex +e −x )<br />
(k) f(x) = x 4/3 +4x 1/3 +3x −2/3 (l) f(x) = 2x √ x+1<br />
(m) f(x) = e −x2<br />
(n) f(x) = sinx 2 , [0,π]<br />
4. Find the absolute maximum and absolute minimum values of f on the given interval.<br />
(a) f(x) = 3x 2 −12x+5, [0,3]<br />
(b) f(x) = 2x 3 +3x 2 +4, [−2,1]<br />
(c) f(x) = x 4 −4x 2 +2, [−3,2]<br />
(d) ) f(x) = x 2 − 2 x , [1 2 ,2]<br />
(e) f(x) = x<br />
x 2 +1 , [0,2]<br />
(f) f(x) = sinx+cosx, [0,π/3]<br />
(g) f(x) = xe −x , [0,2]<br />
(h) f(x) = x−3lnx, [1,4]<br />
(i) f(x) = |x−1|, [0,3]<br />
(j) f(x) = 3√ x, [−1,27]<br />
Answer to <strong>Exercise</strong> <strong>3.3</strong><br />
1. (a) Absolute maximum at b; local maxima at b, e, and r;<br />
absolute minimum at d; local minima at d and s<br />
(b) Absolute maximum at e; local maxima at e and s;<br />
absolute minimum at t; local minima at b, c, d, r, and t<br />
2. (a) Absolute maximum f(4) = 4; absolute minimum f(7) = 0<br />
local maximum f(4) = 4, f(6) = 3; local minimum f(2) = 1, f(5) = 2<br />
(b) Absolute maximum f(7) = 5; absolute minimum f(1) = 0<br />
local maximum f(0) = 2, f(3) = 4, f(5) = 3<br />
local minimum f(1) = 0, f(4) = 2, f(6) = 1
MA111: Prepared by Dr.Archara Pacheenburawana 28<br />
3. (a) − 5 , absolute minimum (b) −1, local maximum; 1, local minimum<br />
2<br />
(c) 1, no local extreme values<br />
9<br />
(d) 0, no local extreme values; , local minimum<br />
4<br />
16<br />
(e) 0, no local extreme values; , local minimum<br />
9<br />
(f) − 2 , local minimum; 2, local maximum<br />
3<br />
(g) π, 5π, local maximum; 3π<br />
, 7π , local minimum<br />
4 4 4 4<br />
(h) 1, no local extreme values<br />
(i) −1, local minimum; 1, local maximum<br />
(j) 0, local minimum (k) −2,1, local minimum<br />
(l) − 2 , local minimum (m) 0, local maximum<br />
3<br />
√<br />
3π<br />
(n) 0, , local minimum; √ √<br />
π<br />
, 5π, local maximum<br />
2 2 2<br />
4. (a) f(0) = 5,f(2) = −7 (b) f(1) = 9,f(−2) = 0 (c) f(−3) = 47,f(± √ 2) = −2<br />
(d) f(2) = 3,f(1) = −1 (e) f(1) = 1 2 ,f(0) = 0 (f) f(π/4) = √ 2,f(0) = 1<br />
(g) f(1) = 1/e,f(0) = 0 (h) f(1) = 1,f(3) = 3−3ln3 (i) f(3) = 2,f(1) = 0<br />
(j) f(27) = 3,f(−1) = −1<br />
<strong>Exercise</strong> 3.4<br />
1. Find the intervals on which f is increasing or decreasing.<br />
(a) f(x) = x 3 −3x+2 (b) f(x) = x 4 −8x 2 +1<br />
(c) f(x) = x 6 +192x+17 (d) f(x) = (x+1) 2/3<br />
(e) f(x) = x−2sinx, [0,2π]<br />
(g) f(x) = e x2 −1<br />
(f) f(x) = sin3x, [0,π]<br />
(h) f(x) = (lnx)/ √ x<br />
2. At what values of x does f have a local maximum or minimum Sketch the graph.<br />
(a) f(x) = x 3 +2x 2 −x−1 (b) f(x) = x √ x 2 +1<br />
(c) f(x) = xe −2x (d) f(x) = lnx 2<br />
(e) f(x) = x (f) f(x) = x3<br />
x 2 −1<br />
x 2 −1<br />
(g) f(x) = sinx+cosx (h) f(x) = √ x 3 +3x 2<br />
(i) f(x) = x 2/3 −2x −1/3<br />
3. Show that 5 is a critical number of g(x) = 2 + (x − 5) 3 but g has no local extreme<br />
values at 5.<br />
4. Find a cubic function f(x) = ax 3 +bx 2 +cx+d that has a local maximum value of 3<br />
at −2 and a local minimum value of 0 at 1.
MA111: Prepared by Dr.Archara Pacheenburawana 29<br />
Answer to <strong>Exercise</strong> 3.4<br />
1. (a) Inc. on (−∞,−1)∪(1,∞); dec. on (−1,1)<br />
(b) Inc. on (−2,0)∪(2,∞); dec. on (−∞,−2)∪(0,2)<br />
(c) Inc. on (−2,∞); dec. on (−∞,−2) (d) Inc. on (−1,∞); dec. on (−∞,−1)<br />
(e) Inc. on ( π , 5π 3 3 )∪(7π,3π); dec. on (0, π 3 3 )∪(5π, 7π ) 3 3<br />
(f) Inc. on (0, π 6 )∪(3π, 5π); dec. on 6 6 (π, 3π 6 6 )∪(5π,π)<br />
6<br />
(g) Inc. on (0,∞); dec. on (−∞,0) (h) Inc. on (0,e 2 ); dec. on (e 2 ,∞)<br />
2. (a) Loc. max. at x = − 2 − √ 7<br />
; loc. min. at x = 3 3 −2 + √ 7<br />
3 3<br />
y<br />
2<br />
2<br />
x<br />
(b) None<br />
10<br />
y<br />
2<br />
x<br />
(c) Loc. max. at x = 1 2<br />
y<br />
0.2<br />
1<br />
x<br />
(d) None<br />
y<br />
1<br />
1<br />
x
MA111: Prepared by Dr.Archara Pacheenburawana 30<br />
(e) None<br />
y<br />
2<br />
1<br />
x<br />
(f) Loc. max. at x = − √ 3; Loc. min. at x = √ 3<br />
y<br />
2<br />
4<br />
x<br />
(g) Loc. max. at x = π +2nπ; Loc. min. at x = 5π +2nπ<br />
4 4<br />
y<br />
2<br />
π<br />
x<br />
(h) Loc. max. at x = −2; Loc. min. at x = 0<br />
y<br />
(i) Loc. min. at x = −1<br />
2<br />
y<br />
1<br />
x<br />
2<br />
2<br />
x<br />
4. f(x) = 1 9 (2x3 +3x 2 −12x+7)
MA111: Prepared by Dr.Archara Pacheenburawana 31<br />
<strong>Exercise</strong> 3.5<br />
1. Use the given graph of f to find the intervals of concavity.<br />
(a)<br />
y<br />
20<br />
10<br />
−3<br />
−1<br />
1 3<br />
x<br />
(b)<br />
y<br />
1<br />
−4<br />
−2<br />
2 4<br />
x<br />
(c)<br />
y<br />
10<br />
5<br />
−2<br />
2 4<br />
x<br />
−5<br />
−10<br />
(d)<br />
y<br />
10<br />
5<br />
−3<br />
−1<br />
1 2 3<br />
x<br />
−5<br />
2. Given the following functions.<br />
• Find the interval of increase and decrease.<br />
• Find the local maximum and minimum values.<br />
• Find the intervals of concavity and the inflection points.
•<br />
•<br />
•<br />
•<br />
MA111: Prepared by Dr.Archara Pacheenburawana 32<br />
• Use the above information to sketch the graph.<br />
(a) f(x) = 2x 3 −3x 2 −12x (b) f(x) = x 4 −6x 2<br />
(c) f(x) = 3x 5 −5x 3 +3 (d) f(x) = x √ x 2 +1<br />
(e) f(x) = x 1/3 (x+3) 2/3 (f) f(x) = sin 2 x<br />
Answer to <strong>Exercise</strong> 3.5<br />
1. (a) CU on (−∞,−1)∪(1,∞); CD on (−1,1)<br />
(b) CU on (−∞,0); CD on (0,∞)<br />
(c) CU on (1,∞); CD on (−∞,1)<br />
(d) CU on (−1,0)∪(1,∞); CD on (−∞,−1)∪(0,1)<br />
2. (a) Inc. on (−∞,−1)∪(2,∞); dec. on (−1,2); loc. max. f(−1) = 7;<br />
loc. min. f(2) = −20; CU on ( 1,∞); CD on (−∞, 1); IP 2 2 (1 2 ,−13)<br />
2<br />
y<br />
−10<br />
5<br />
1<br />
x<br />
−20<br />
(b) Inc. on (− √ 3,0)∪( √ 3,∞); dec. on (−∞,− √ 3)∪(0, √ 3);<br />
loc. min. f(± √ 3) = −9; loc. max. f(0) = 0; CU on (−∞,−1)∪(1,∞);<br />
CD on (−1,1); IP (±1,−5)<br />
y<br />
−1<br />
1<br />
• •<br />
x<br />
• •<br />
−10<br />
(c) Inc. on (−∞,−1)∪(1,∞); dec. on (−1,−1); loc. max. f(−1) = 5;<br />
loc. min. f(1) = 1; CU on (−1/ √ 2,0)∪(1/ √ 2,∞);<br />
CD on (−∞,−1/ √ 2)∪(1/ √ 2,∞); IP (0,3), (±1/ √ 2,3∓ 8√ 7 2)
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
MA111: Prepared by Dr.Archara Pacheenburawana 33<br />
y<br />
5<br />
−1<br />
1<br />
x<br />
(d) Inc. on (−∞,∞); No loc. max and loc. min; CU on (0,∞);<br />
CD on (−∞,0); IP (0,0)<br />
y<br />
x<br />
e) Inc. on (−∞,−3)∪(−1,∞); dec. on (−3,−1); loc. max. f(−3) = 0;<br />
loc. min. f(−1) = − 3√ 4; CU on (−∞,−3)∪(−3,0); CD on (0,∞); IP (0,0)<br />
y<br />
2<br />
1<br />
x<br />
(f) Inc. on (0,π/2)∪(π,3π/2); dec. on (π/2,π)∪(3π/2,2π)<br />
loc. max. f(π/1) = f(3π/2) = 1; loc. min. f(π) = 0<br />
CU on (0,π/4)∪(3π/4,5π/4)∪(7π/4,2π); CD on (π/4,3π/4)∪(5π/4,7π/4)<br />
IP (π/4, 1),(3π/4, 1),(5π/4, 1),(7π/4, 1)<br />
2 2 2 2<br />
y<br />
1<br />
0<br />
π<br />
2<br />
π<br />
3π<br />
2<br />
2π<br />
x
MA111: Prepared by Dr.Archara Pacheenburawana 34<br />
<strong>Exercise</strong> 3.6<br />
1. Find two positive numbers whose product is 100 and whose sum is minimum.<br />
2. Find two numbers whose product is −16 and the sum of whose squares is minimum.<br />
3. Forwhatnumber doestheprincipal fourthrootexceed twicethenumberbythelargest<br />
amount.<br />
4. Find the dimensions of a rectangle with area 1000 m 2 whose perimeter is as small as<br />
possible.<br />
5. A box with a square base and open top must have the volume of 32,000 cm 3 . Find<br />
the dimensions of the box that minimize the amount of material used.<br />
6. If 1200 cm 2 of material is available to make a box with a square base and an open<br />
top, find the largest possible volume of the box.<br />
7. A farmer wishes to fence off two identical adjoining rectangular pens, each with 900<br />
square feet of area, as shown in the following Figure.<br />
y<br />
x<br />
What are x and y so that the least amount of fence is required<br />
8. Find the point on the line y = 4x+7 that is closest to the origin.<br />
9. Find the point on the line 6x+y = 9 that is closest to the point (−3,1).<br />
10. Find the point on the parabola y = x 2 that is closest to the point (0,5).<br />
11. Find the point on the parabola x+y 2 = 0 that is closest to the point (0,−3).<br />
12. Find the dimensions of the rectangle of largest area that can be inscribed in a circle<br />
of radius r.<br />
13. Find the dimensions of the isosceles triangle of largest area that can be inscribed in a<br />
circle of radius r.<br />
14. A right circular cylinder is inscribed in a cone with height h and base radius r. Find<br />
the largest possible volume of such a cylinder.<br />
15. A right circular cylinder is inscribed in a sphere of radius r. Find the largest possible<br />
surface area of such a cylinder.<br />
16. A right circular cylinder is inscribed in a sphere of radius r. Find the largest possible<br />
volume of such a cylinder.<br />
17. Show that the rectangle with maximum perimeter that can be inscribed in a circle is<br />
a square.
MA111: Prepared by Dr.Archara Pacheenburawana 35<br />
18. (a) Show that of all the rectangles with a given area, the one with smallest perimeter<br />
is a square.<br />
(b) Show that of all the rectangles with a given perimeter, the one with largest area<br />
is a square.<br />
19. At 7 : 00am. one ship was 60 miles due east from a second ship. If the first ship<br />
sailed west at 20 miles per hour and the second ship sailed southeast at 30 miles per<br />
hour, when were they closest together<br />
20. A piece of wire 10 m long is cut into two pieces. One piece is bent into a square and<br />
the other is bent into an equilateral triangle. How should the wire be cut so that the<br />
total area enclosed is (a) a maximum (b) A minimum<br />
Answer to <strong>Exercise</strong> 3.6<br />
1. 10,10 2. −4,4 3.<br />
1<br />
16<br />
4. 10 √ 10×10 √ 10 5. 40×40×20 6. 4,000 cm 3<br />
7. 15 √ 3×20 √ 3 8. ( − 28,<br />
)<br />
7<br />
17 17<br />
9. ( − 45,<br />
)<br />
63<br />
37 37<br />
10.<br />
( ) (<br />
−√ 3<br />
2<br />
, 9 2<br />
,<br />
3√<br />
2<br />
, 9 2<br />
11. (−1,−1) 12. √ 2r × √ 2r 13. Base √ 3r, height 3r/2 14.<br />
4<br />
27 πr2 h<br />
15. πr 2( 1+ √ 5 ) 16. 4πr 3 /3 √ 3 19. 8 : 09am.<br />
20. (a) Use all of the wire for the square (b) 40 √ 3/ ( 9+4 √ 3 ) m for the square<br />
<strong>Exercise</strong> 3.7<br />
1. Verify that the function satisfies the three hypotheses of Rolle’s Theorem on the given<br />
interval. Then find all numbers c that satisfy the conclusion of Rolle’s Theorem.<br />
(a) f(x) = x 2 −4x+1, [0,4] (b) f(x) = x 3 −3x 2 +2x+5, [0,2]<br />
(c) f(x) = sin2πx, [−1,1]<br />
(d) f(x) = x √ x+6, [−6,0]<br />
2. Use the graph of f to estimate the values of c that satisfy the conclusion of the Mean<br />
Value Theorem for the interval [0,8].<br />
y<br />
)<br />
y = f(x)<br />
1<br />
1<br />
x
MA111: Prepared by Dr.Archara Pacheenburawana 36<br />
3. Verify that the function satisfies the hypotheses of the Mean Value Theorem on the<br />
given interval. Then find all numbers c that satisfy the conclusion of the Mean Value<br />
Theorem.<br />
(a) f(x) = 3x 2 +2x+5, [−1,1] (b) f(x) = x 3 −x, [0,2]<br />
(c) f(x) = e −2x , [0,3] (d) f(x) = x<br />
x+2 , [1,4]<br />
Answer to <strong>Exercise</strong> 3.7<br />
1. (a) 2 (b) 3±√ 3<br />
3<br />
(c) ± 1 4 ,±3 4<br />
(d) −4 2. 0.8, 3.2, 4.4, 6.1<br />
3. (a) 0 (b) 2 √<br />
3<br />
(c) − 1 2 ln[(1−e−6 )/6] (d) 3 √ 2−2<br />
<strong>Exercise</strong> 4.1<br />
1. Find the most general antiderivative of the function.<br />
(a) f(x) = 5 (b) f(x) = x 2 +π<br />
(c) f(x) = x 5/4 (d) f(x) = 1/ 3√ x 2<br />
(e) f(x) = x 2 −x (f) f(x) = 4x 5 −x 3<br />
(g) f(x) = 27x 7 +3x 5 −45x 3 + √ 2x<br />
(h) f(x) = 3 x 2 − 2 x 3 (i) f(x) = 4x6 +3x 4<br />
2. Evaluate the integral and check your answer by differentiating.<br />
∫<br />
∫<br />
(a) 3x 4 dx<br />
(b) (x 2 +x)dx<br />
∫<br />
∫<br />
(c) (3x 4 −3x)dx (d) (x+1) 2 dx<br />
∫<br />
(e) 3 √ ∫<br />
xdx (f)<br />
(3− 1 )<br />
dx<br />
x<br />
∫ 4 x 1/3 ∫<br />
−3<br />
(x 2 +1) 2<br />
(g) dx (h) √ dx<br />
x 2/3 x<br />
∫<br />
∫<br />
(i) (sinx−cosx)dx (j) 2secxtanxdx<br />
∫<br />
∫<br />
(k) 5sec 2 xdx (l) (3e x −2)dx<br />
∫<br />
∫<br />
(m) (3cosx−1/x)dx (n)<br />
(5x− 3 )<br />
dx<br />
e<br />
∫ x e x ∫<br />
+3<br />
(o) dx (p) x 1/4 (x 5/4 −4)dx<br />
e x<br />
x 3
MA111: Prepared by Dr.Archara Pacheenburawana 37<br />
Answer to <strong>Exercise</strong> 4.1<br />
1. (a) 5x+C (b) 1 3 x3 +πx+C (c) 4 9 x9/4 +C (d) 3 3√ x+C (e) 1 3 x3 − 1 2 x2 +C<br />
(f) 2 3 x6 − 1 4 x4 +C (g) 27<br />
8 x8 + 1 2 x6 − 45 4 x4 + √ 2<br />
2 x2 +C (h) − 3 x + 1 x 2 +C<br />
(i) x 4 + 3 2 x2 +C<br />
2. (a) 3 5 x5 +C (b) 1 3 x3 + x2<br />
2 +C (c) 3 5 x5 − 3 2 x2 +C (d) 1 3 (x+1)3 +C<br />
(e) 2x 3/2 +C (f) 3x+ 1 3 x−3 +C (g) 3 2 x2/3 −9x 1/3 +C (h) 2 9 x9/2 + 4 5 x5/2 +2x 1/2 +C<br />
(i) −cosx−sinx+C (j) 2secx+C (k) 5tanx+C (l) 3e x −2x+C<br />
(m) 3sinx−ln|x|+C (n) 5 2 x2 +3e −x +C (o) x−3e −x +C (p) 2 5 x5/2 − 16 5 x5/4<br />
<strong>Exercise</strong> 4.2<br />
1. Evaluate the integral by making the given substitution.<br />
∫<br />
(a) cos3xdx, u = 3x<br />
∫<br />
(b) x 2 (x 3 +2)dx, u = x 3 +2<br />
∫<br />
4<br />
(c) dx, u = 1+2x<br />
(1+2x)<br />
3<br />
∫ √ ( x+2)<br />
3<br />
(d) √ dx, u = √ x+2 x<br />
2. Evaluate the indefinite integral<br />
∫<br />
(a) 2x(x 2 +3) 4 dx<br />
∫ √x−1dx<br />
(c)<br />
∫<br />
(e)<br />
∫<br />
(g)<br />
dx<br />
5−3x<br />
1+4x<br />
√ dx<br />
1+x+2x<br />
2<br />
∫<br />
(i) cos2xdx<br />
∫<br />
(k) xsin(x 2 )dx<br />
∫<br />
(m) cos 4 xsinxdx<br />
∫<br />
(o) secxtanx √ 1+secxdx<br />
∫<br />
(b) (2x+1)(x 2 +x) 3 dx<br />
∫<br />
x 2<br />
(d) √<br />
x3 −2 dx<br />
∫<br />
(f)<br />
∫<br />
(h)<br />
2x+1<br />
x 2 +x−1 dx<br />
1<br />
√ √ dx x( x+1)<br />
2<br />
∫<br />
(j) cosx √ sinx+1dx<br />
∫<br />
sinx<br />
(l) √ dx cosx<br />
∫<br />
(n) sinx(cosx+3) 3/4 dx<br />
∫<br />
(p) cosxe sinx dx
MA111: Prepared by Dr.Archara Pacheenburawana 38<br />
∫<br />
(q) e x√ ∫<br />
1+e x dx (r) xe x2 +1 dx<br />
∫<br />
∫<br />
dx<br />
4<br />
(s)<br />
(t)<br />
xlnx<br />
x(lnx+1) dx 2<br />
∫ √cotx<br />
∫<br />
(u) csc 2 xdx (v) sinx(cosx−1) 3 dx<br />
∫<br />
∫ e<br />
(w) sec 3 x −e −x<br />
xtanxdx (x) dx<br />
e x +e−x ∫ ∫ 1+x<br />
2x+3<br />
(y)<br />
1+x dx (z) 2 x+7 dx<br />
Answer to <strong>Exercise</strong> 4.2<br />
1. (a) 1 3 sin3x+C (b) 2 3 (x3 +2) 3/2 +C (c) −1/(1+2x) 2 +C (d) 1 2 (√ x+2) 4 +C<br />
2. (a) 1 5 (x2 +3) 5 +C (b) 1 4 (x2 +x) 4 +C (c) 2 3 (x−1)3/2 +C (d) 2 3√<br />
x3 −2+C<br />
(e) − 1 3 ln|5−3x|+C (f) ln|x2 +x−1|+C (g) 2 √ 1+x+2x 2 +C<br />
(h) −2( √ x+1) −1 +C (i) 1 2 sin2x+C (j) 2 3 (sinx+1)3/2 +C (k) − 1 2 cos(x2 )+C<br />
(l) −2 √ cosx+C (m) − 1 5 cos5 x+C (n) − 4 7 (cosx+3)7/4 +C<br />
(o) 2 3 (1+secx)3/2 +C (p) e sinx +C (q) 2 3 (1+ex ) 3/2 +C (r) 1 2 ex2 +1 +C<br />
(s) ln|lnx|+C (t) −4(lnx+1) −1 +C (u) − 2 3 (cotx)3/2 +C (v) − 1 4 (cosx−1)4 +C<br />
(w) 1 3 sec3 x+C (x) ln(e x +e −x )+C (y) tan −1 x+ 1 2 ln(1+x2 )+C<br />
(z) 2(x+7)−11ln|x+7|+C<br />
<strong>Exercise</strong> 4.3<br />
1. Express the limit as a definite integral on the given interval.<br />
(a) lim<br />
n→∞<br />
n∑<br />
i=1<br />
x i sinx i △x, [0,π]<br />
n∑ e x i<br />
(b) lim △x, [1,5]<br />
n→∞ 1+x<br />
i=1 i<br />
(c) lim<br />
n∑<br />
n→∞<br />
i=1<br />
n∑<br />
n→∞<br />
(d) lim<br />
i=1<br />
[2(x ∗ i) 2 −5x ∗ i]△x, [0,1]<br />
√<br />
x<br />
∗<br />
i △x, [1,4]
MA111: Prepared by Dr.Archara Pacheenburawana 39<br />
2. Use the form of the definition of the integral given in (4.7) to evaluate the integral.<br />
(a)<br />
(c)<br />
(e)<br />
∫ 1<br />
0<br />
∫ 5<br />
1<br />
∫ 5<br />
0<br />
3. Prove that<br />
4. Prove that<br />
2xdx<br />
(2+3x−x 2 )dx<br />
(1+2x 3 )dx<br />
∫ b<br />
a<br />
∫ b<br />
a<br />
xdx = b2 −a 2<br />
.<br />
2<br />
x 2 dx = b3 −a 3<br />
.<br />
3<br />
(b)<br />
(d)<br />
(f)<br />
∫ 5<br />
−1<br />
∫ 2<br />
0<br />
∫ 2<br />
1<br />
(1+3x)dx<br />
(2−x 2 )dx<br />
x 3 dx<br />
5. Write the given sum or difference as a single integral in the form ∫ b<br />
f(x)dx. a<br />
6. If<br />
7. If<br />
(a)<br />
(c)<br />
(e)<br />
1. (a)<br />
∫ 8<br />
2<br />
∫ 1<br />
∫ 2<br />
0<br />
∫ 2<br />
0<br />
∫ 3<br />
f(x)dx+<br />
f(x)dx+<br />
f(x)dx+<br />
∫ 3<br />
2<br />
∫ 1<br />
2<br />
∫ 6<br />
1 3<br />
f(x)dx = 1.8 and<br />
f(x)dx = 3,,<br />
∫ 4<br />
f(x)dx<br />
f(x)dx<br />
f(x)dx+<br />
∫ 8<br />
5<br />
(b)<br />
(d)<br />
∫ 3<br />
0<br />
∫ 2<br />
f(x)dx−<br />
f(x)dx+<br />
∫ 3<br />
2<br />
∫ 3<br />
−1 2<br />
∫ 12<br />
6<br />
f(x)dx<br />
f(x)dx = 3.2, find<br />
f(x)dx = −7, and<br />
∫ 4<br />
∫ 5<br />
2<br />
f(x)dx.<br />
f(x)dx = 2, find<br />
f(x)dx<br />
f(x)dx<br />
0<br />
0<br />
3<br />
1<br />
∫ π<br />
0<br />
xsinxdx (b)<br />
Answer to <strong>Exercise</strong> 4.3<br />
∫ 5<br />
1<br />
e x ∫ 1<br />
1+x dx (c)<br />
2. (a) 1 (b) 42 (c) 2 (d) 4 3<br />
(e) 317.5 (f) 3.75<br />
5. (a)<br />
∫ 3<br />
f(x)dx (b)<br />
∫ 2<br />
f(x)dx (c)<br />
∫ 1<br />
(2x 2 −5x)dx (d)<br />
0<br />
1<br />
f(x)dx (d)<br />
∫ 3<br />
∫ 4<br />
f(x)dx.<br />
√ xdx<br />
0<br />
0<br />
0<br />
−1 1<br />
6. −1.4 7. −12<br />
∫ 3<br />
f(x)dx (e)<br />
∫ 12<br />
f(x)dx
MA111: Prepared by Dr.Archara Pacheenburawana 40<br />
<strong>Exercise</strong> 4.4<br />
1. Evaluate the definite integrals using the First Fundamental Theorem of Calculus.<br />
(a)<br />
(c)<br />
(e)<br />
(g)<br />
(i)<br />
(k)<br />
(m)<br />
(o)<br />
(q)<br />
(s)<br />
(t)<br />
∫ 3<br />
−1<br />
∫ 4<br />
0<br />
∫ 2<br />
1<br />
∫ 3<br />
3<br />
∫ π<br />
π/2<br />
∫ 9<br />
1<br />
∫ 9<br />
8<br />
∫ π/2<br />
π/6<br />
∫ 2<br />
0<br />
∫ 3<br />
−2<br />
∫ 2<br />
0<br />
x 5 dx<br />
(b)<br />
∫ 2<br />
0<br />
(2x−3)dx<br />
∫<br />
√ 4<br />
xdx (d) ( √ x+3x)dx<br />
∫<br />
3<br />
1<br />
x dx (f) (x √ x+x −1/2 )dx<br />
4 0<br />
√<br />
∫ π/2<br />
x5 +2dx (h) 2sinxdx<br />
secxtanxdx<br />
(j)<br />
0<br />
0<br />
∫ π<br />
π/2<br />
(2sinx−cosx)dx<br />
∫<br />
1<br />
1<br />
2x dx (l) (e x −e −x )dx<br />
2 x dx (n)<br />
(<br />
x+ 2 )<br />
sin 2 dx<br />
x<br />
(p)<br />
|2x−3|dx<br />
(r)<br />
0<br />
∫ 3<br />
0<br />
∫ √ 3<br />
1<br />
∫ 3π/4<br />
0<br />
(3e x −x 2 )dx<br />
6<br />
1+x 2 dx<br />
|cosx|dx<br />
{ −x, x ≥ 0<br />
f(x)dx, where f(x) =<br />
x 2 , x < 0<br />
{ x<br />
f(x)dx, where f(x) =<br />
4 , 0 ≤ x < 1<br />
x 5 , 1 ≤ x ≤ 2<br />
2. Use the Second Fundamental Theorem of Calculus to find the derivative.<br />
∫ x<br />
∫ x √<br />
(a) f(x) = (t 2 −3t+2)dt (b) g(x) = 1−2tdt<br />
(c) g(y) =<br />
(e) f(x) =<br />
(g) h(x) =<br />
(i) y =<br />
∫ 1<br />
0<br />
∫ y<br />
1−3x<br />
2<br />
∫ x 2<br />
0<br />
∫ 1/x<br />
2<br />
t 2 sintdt (d) F(x) =<br />
(e −t2 +1)dt (f) f(x) =<br />
arctantdt (h) y =<br />
0<br />
∫ 2<br />
x<br />
∫ −1<br />
x<br />
∫ √ x<br />
u 3<br />
∫ x 3<br />
1+u du (j) y = 2<br />
3<br />
cos(t 2 )dt<br />
cost<br />
t<br />
ln(t 2 +1)dt<br />
dt<br />
√ x<br />
√<br />
tsintdt
MA111: Prepared by Dr.Archara Pacheenburawana 41<br />
Answer to <strong>Exercise</strong> 4.4<br />
1. (a) 364<br />
3<br />
(b) −2 (c) 16 3<br />
(d) 88<br />
3<br />
(e) 7 8<br />
(f) 12<br />
5<br />
(g) 0 (h) 2 (i) Does not exist<br />
(j) 3 (k) ln3 (l) e+e −1 −2 (m) 28<br />
ln2<br />
(q) 5 2<br />
(r) 2− √ 2<br />
2<br />
(s) − 11 6<br />
(t) 10.7<br />
(n) 3e 3 −12 (o) π2<br />
9 +2√ 3 (p) π 2<br />
2. (a) f ′ (x) = x 2 −3x+2 (b) g ′ (x) = √ 1+2x (c) g ′ (y) = y 2 siny<br />
(d) F ′ (x) = −cos(x 2 ) (e) f ′ (x) = (e −x4 +1)2x (f) f ′ (x) = −ln(x 2 +1)<br />
(g) h ′ (x) = −arctan(1/x)/x 2 (h) y ′ = cos√ x<br />
2x<br />
(j) y ′ = 3x 7/2 sin(x 3 )−(sin √ x)/(2 4√ x)<br />
Evaluate the definite integral, if it exists.<br />
1.<br />
3.<br />
5.<br />
7.<br />
9.<br />
11.<br />
13.<br />
15.<br />
∫ 2<br />
0<br />
∫ 1<br />
0<br />
∫ 1<br />
0<br />
∫ 4<br />
1<br />
∫ 3<br />
(x−1) 25 dx 2.<br />
x 2 (1+2x 3 ) 5 dx 4.<br />
<strong>Exercise</strong> 4.5<br />
∫ 2<br />
0<br />
∫ 1<br />
−1<br />
∫ π<br />
(i) y ′ = 3(1−3x)3<br />
1+(1−3x) 2<br />
x √ x 2 +1dx<br />
x<br />
(x 2 +1) 2 dx<br />
4cosx<br />
(sinx+1) 2 dx<br />
cosπxdx 6.<br />
π/2<br />
√<br />
1<br />
1+ 1 ∫ π/2<br />
x 2 x dx 8. cotxdx<br />
dx<br />
2x+3<br />
0<br />
∫ π/3<br />
0<br />
∫ 2<br />
1<br />
∫ a<br />
0<br />
10.<br />
π/4<br />
∫ 4<br />
∫<br />
sinx<br />
13<br />
cos 2 x dx 12.<br />
x √ x−1dx 14.<br />
x √ x 2 +a 2 dx (a > 0)<br />
1<br />
0<br />
∫ e 4<br />
e<br />
x−1<br />
√ x<br />
dx<br />
dx<br />
√<br />
3 (1+2x)<br />
2<br />
dx<br />
x √ lnx<br />
Answer to <strong>Exercise</strong> 4.5<br />
1. 0 2. 5 3√<br />
5−<br />
1<br />
3<br />
3. 81<br />
4<br />
4. 0 5. 0 6. −2 7.<br />
4 √ 2<br />
3<br />
− 5√ 5<br />
12<br />
8. 1 2 ln2 9. 1 2 ln3<br />
10.<br />
8<br />
3<br />
11. 1 12. 3 13. 16<br />
15<br />
14. 2 15. 1 3 (2√ 2−1)a 3
MA111: Prepared by Dr.Archara Pacheenburawana 42<br />
1. Find the area of the shaded region.<br />
<strong>Exercise</strong> 5.1<br />
(a)<br />
y<br />
y = x 2 +1<br />
−1 2<br />
x<br />
(b)<br />
y<br />
y = x 2 +2<br />
y = −x<br />
−1<br />
2 x<br />
(c)<br />
y<br />
y = 2−x 2<br />
y = x<br />
x<br />
2. Find the area of the region bounded by the given curves.<br />
(a) y = x 2 +3, y = x, −1 ≤ x ≤ 1<br />
(b) y = x 3 , y = x 2 −1, 1 ≤ x ≤ 3<br />
(c) y = x+1, y = 9−x 2 , −1 ≤ x ≤ 2
MA111: Prepared by Dr.Archara Pacheenburawana 43<br />
(d) y = e x , y = x−1, −2 ≤ x ≤ 0<br />
(e) y = x+1, y = (x−1) 2 , −1 ≤ x ≤ 2<br />
(f) y = x 2 −1, y = 1−x, 0 ≤ x ≤ 2<br />
(g) y = cosx, y = sin2x, 0 ≤ x ≤ π/2<br />
(h) y = x 3 −1, y = 1−x, −2 ≤ x ≤ 2<br />
3. Find the area of the region enclosed by the given curves.<br />
(a) y = x 2 −1, y = 7−x 2<br />
(b) y = x 2 +1, y = 3x−1<br />
(c) y = x 3 , y = 3x+2<br />
(d) y = x 3 , y = x 2<br />
(e) y = x, y = 2−x, y = 0<br />
(f) x = 3y, x = 2+y 2<br />
(g) x = y, x = −y, x = 1<br />
(h) y = x, y = 2, y = 6−x, y = 0<br />
(i) x = 1−y 2 , x = y 2 −1<br />
(j) y = cosx, y = 1−2x/π<br />
(k) y = x 2 , y = 2/(x 2 +1)<br />
(l) x = y 3 −y, x = 1−y 4<br />
Answer to <strong>Exercise</strong> 5.1<br />
1. (a) 6 (b) 40 3<br />
(c) 9 2<br />
2. (a) 20 (b) 40 (c) 19.5 (d) −e −2 (e) 31 (f) 3 (g) 1 (h) 29<br />
3 3 6 2 2<br />
3. (a) 64<br />
3<br />
(b) 1 6<br />
(c) 27<br />
4<br />
(d) 1<br />
12<br />
(e) 1 (f) 1 6<br />
(g) 1 (h) 8 (i) 1 8<br />
(j) 2− π 2<br />
(k) π − 2 3<br />
(l) 8 5<br />
<strong>Exercise</strong> 5.2<br />
1. Findthevolumeofthesolidobtainedbyrotatingtheregionboundedbyy = 2−x, y =<br />
0, and x = 0 (a) about the x-axis (b) about the line y = 3.<br />
2. Find the volume of the solid obtained by rotating the region bounded by y = √ x, y =<br />
2, and x = 0 (a) about the y-axis (b) about the line x = 4.<br />
3. Find the volume of the solid obtained by rotating the region bounded by y = e x , x =<br />
0, x = 2, and y = 0 (a) about the y-axis (b) about the line y = −2.
MA111: Prepared by Dr.Archara Pacheenburawana 44<br />
4. Findthevolumeofthesolidobtainedbyrotatingtheregionboundedbyy = x 3 , y = 0,<br />
and x = 1 (a) about the y-axis (b) about the x-axis.<br />
5. The region R enclosed by the curves y = 3−x, the x-axis, and the y-axis. Find the<br />
volume of the solid obtained by rotating the region R (a) about the y-axis, (b) about<br />
the x-axis (c) about the line y = 3, (d) about the line y = −3, (e) about the line<br />
x = 3, and (f) about the line x = −3.<br />
6. The region R enclosed by the curves y = x 2 , y = 0, and x = 1. Find the volume of<br />
the solid obtained by rotating the region R (a) about the y-axis, (b) about the x-axis,<br />
(c) about the line x = 1, (d) about the line y = 1, (e) about the line x = −1, and (d)<br />
about the line y = −1.<br />
1. (a) 8π 3<br />
4. (a) 2π 5<br />
(b) 28π<br />
3<br />
(b) π 7<br />
Answer to <strong>Exercise</strong> 5.2<br />
2. (a) 32π<br />
5<br />
(b) 224π<br />
15<br />
( e<br />
4<br />
3. (a) 2πe 2 +2π (b) π<br />
2 +4e2 − 9 )<br />
2<br />
5. (a) 9π (b) 9π (c) 18π (d) 36π (e) 18π (f) 36π<br />
6. (a) π 2<br />
(b) π 5<br />
(c) π 6<br />
(d) 7π<br />
15<br />
(e) 7π 6<br />
(f) 13π<br />
15<br />
<strong>Exercise</strong> 5.3<br />
1. Use the method of cylindrical shells to find the volume generated by rotating the<br />
region bounded by the given curve about the y-axis.<br />
(a) y = 1 , y = 0, x = 1, x = 2<br />
x<br />
(b) y = e −x2 , y = 0, x = 0, x = 1<br />
(c) y 2 = x, x = 2y<br />
2. Usethemethodofcylindricalshellstofindthevolumeofthesolidobtainedbyrotating<br />
the region bounded by the given curve about the x-axis.<br />
(a) x = 1+y 2 , x = 0, y = 1, y = 2<br />
(b) y = x 2 , y = 9<br />
(c) y = √ x, y = 0, x+y = 2<br />
3. Use the appropriate method to find the volume generated by rotating the region<br />
bounded by the given curve about the specified axis.<br />
(a) y = √ x, x = 3, y = 0; about y-axis<br />
(b) y = √ x, x = 5, y = 0; about x = 5<br />
(c) y = 1 4 x3 +1, y = 1−x, x = 1; about y-axis<br />
(d) x = y 2 , y = 1, x = 0; about x-axis<br />
(e) x = y 2 , y = 2, x = 0; about y = 2
MA111: Prepared by Dr.Archara Pacheenburawana 45<br />
Answer to <strong>Exercise</strong> 5.3<br />
1. (a) 2π (b) π(1−1/e) (c) 64π/15 2. (a) 21π/2 (b) 1944π/5 (c) 5π/6<br />
3. (a) 36√ 3<br />
5<br />
π (b) 40√ 5<br />
3<br />
π (c) 23π<br />
30<br />
(d) π 2<br />
(e) 8π 3<br />
Find the length of the curve.<br />
<strong>Exercise</strong> 5.4<br />
1. y = 1 3 (x2 +2) 3/2 , 0 ≤ x ≤ 1<br />
2. y = x4<br />
4 + 1<br />
8x 2, 1 ≤ x ≤ 3<br />
3. y = ln(secx), 0 ≤ x ≤ π/4<br />
4. y = ln(1−x 2 ), 0 ≤ x ≤ 1 2<br />
5. y = coshx, 0 ≤ x ≤ 1<br />
Answer to <strong>Exercise</strong> 5.4<br />
1.<br />
4<br />
3<br />
2. 181<br />
9<br />
3. ln( √ 2+1) 4. ln3− 1 2<br />
5. sinh1<br />
<strong>Exercise</strong> 6.1<br />
Evaluate the integral.<br />
∫<br />
∫<br />
1. xe 2x dx 2. x 2 lnxdx<br />
∫<br />
∫<br />
3. xsin4xdx 4. x 2 e −3x dx<br />
∫<br />
∫<br />
5. x 2 cos3xdx 6. e x sin4xdx<br />
∫<br />
∫<br />
7. (lnx) 2 dx 8. cosxcos2xdx<br />
∫<br />
∫<br />
9. xsec 2 xdx 10. cosxln(sinx)dx<br />
∫<br />
∫<br />
11. cos(lnx)dx 12. cos −1 xdx<br />
∫<br />
13. sin √ ∫ 1<br />
xdx 14. xsin2xdx<br />
15.<br />
17.<br />
∫ 1<br />
0<br />
∫ 4<br />
1<br />
xe −x dx 16.<br />
ln √ xdx 18.<br />
0<br />
∫ 2<br />
1<br />
∫ 2<br />
1<br />
lnx<br />
x 2 dx<br />
x 4 (lnx) 2 dx
MA111: Prepared by Dr.Archara Pacheenburawana 46<br />
Answer to <strong>Exercise</strong> 6.1<br />
1.<br />
1<br />
2 xe2x − 1 4 e2x +C 2. 1 3 x2 lnx− 1 9 x3 +C 3. − 1 4 xcos4x+ 1 16 sin4x+C<br />
4. − 1 3 x2 e −3x − 2 9 xe−3x − 2 27 e−3x +C 5. 1 3 x2 cos3x+ 2 9 xcos3x− 2 27 sin3x+C<br />
6.<br />
1<br />
17 ex sin4x− 4<br />
17 ex cos4x+C 7. x(lnx) 2 −2xlnx+2x+C<br />
8.<br />
2<br />
sin2xcosx− 1 cos2xsinx+C 9. xtanx+ln|cosx|+C<br />
3 3<br />
10. sinxln(sinx)−sinx+C 11. 1 2 x[sin(lnx)+cos(lnx)]+C<br />
12. xcos −1 x− √ 1−x 2 +C 13. −2 √ xcos √ x+2sin √ x+C 14. 1 4 sin2− 1 2 cos2<br />
15. 1− 2 16. 1 − 1 ln2 17. 2ln4− 3 18. 3 e 2 2 2 2 (ln2)2 − 64 62<br />
ln2+<br />
25 125<br />
<strong>Exercise</strong> 6.2<br />
Evaluate the integral.<br />
∫<br />
∫<br />
1. cosxsin 4 xdx 2. cos 2 xsinxdx<br />
∫ 3π/4<br />
∫<br />
3. sin 5 xcos 3 xdx 4. cos 5 xsin 4 xdx<br />
π/2<br />
∫ π/2<br />
∫<br />
5. sin 2 3xdx 6. cos 2 xsin 2 xdx<br />
0<br />
∫<br />
∫ π/4<br />
7. (1−sin2x) 2 dx 8. sin 4 xcos 2 xdx<br />
0<br />
∫<br />
9. sin 3 x √ ∫<br />
cosxdx 10. cos 2 xtan 3 xdx<br />
∫ ∫<br />
1−sinx<br />
11.<br />
cosx dx<br />
12. tan 2 xdx<br />
∫<br />
∫<br />
13. sec 4 xdx 14. tan 5 xdx<br />
∫<br />
∫ π/4<br />
15. tanxsec 3 xdx 16. tan 4 xsec 2 xdx<br />
∫<br />
17. tan 3 xsecxdx 18.<br />
0<br />
∫ π/3<br />
0<br />
tan 3 xsecxdx<br />
∫ sec 2 ∫<br />
x<br />
π/2<br />
19.<br />
cotx dx 20. cot 2 xdx<br />
π/6<br />
∫<br />
∫<br />
21. cot 3 xcsc 3 xdx 22. cot 2 ωcsc 4 ωdω
MA111: Prepared by Dr.Archara Pacheenburawana 47<br />
23.<br />
25.<br />
27.<br />
∫<br />
cscxdx 24.<br />
∫ 1−tan 2 x<br />
dx<br />
sec 2 x<br />
∫<br />
26.<br />
cos7θcos5θdθ 28.<br />
∫ sinx<br />
tanx dx<br />
∫<br />
sin5xsin2xdx<br />
∫<br />
sin4xcos5xdx<br />
Answer to <strong>Exercise</strong> 6.2<br />
1.<br />
1<br />
5 sin5 x+C 2. − 1 3 cos3 x+C 3. − 11<br />
384<br />
4. 1 5 sin5 x− 2 7 sin7 x+ 1 9 sin9 x+C<br />
5.<br />
π<br />
4<br />
6.<br />
1<br />
8 x− 1<br />
32 sin4x+C 7. 3 2 x+cos2x− 1 8 sin4x+C 8. 1<br />
192 (3π−4)<br />
9. [ 2 7 cos3 x− 2 3 cosx]√ cosx+C 10. 1 2 cos2 x−ln|cosx|+C 11. ln(1+sinx)+C<br />
12. tanx−x+C 13. 1 3 tan3 x+tanx+C 14. 1 4 sec4 x−tan 2 x+ln|secx|+C<br />
15.<br />
1<br />
3 sec3 x+C 16. 1 5<br />
17. 1 3 sec3 x−secx+C 18. 38<br />
15<br />
19. 1 2 tan2 x+C<br />
20. √ 3− π 3<br />
21. − 1 5 csc5 x+ 1 3 csc3 x+C 22. − 1 3 cot3 ω − 1 5 cot5 ω +C<br />
23. ln|cscx−cotx|+C 24. sinx+C 25. 1 2 sin2x+C 26. 1 6 sin3x− 1<br />
14 sin7x+C<br />
27.<br />
1<br />
4 sin2θ+ 1 24 sin12θ+C 28. 1 2 cosx− 1<br />
18 cos9x+C<br />
<strong>Exercise</strong> 6.3<br />
Evaluate the integral.<br />
∫ 2<br />
1.<br />
t 3√ t 2 −1 dt<br />
∫<br />
1<br />
3.<br />
x 2√ 25−x dx<br />
∫<br />
2 x 2<br />
5. √<br />
x2 +9 dx<br />
√<br />
2<br />
1<br />
2. ∫<br />
4. ∫<br />
2<br />
√<br />
x2 −4 dx<br />
dx<br />
x √ x 2 +3 dx<br />
6. ∫ √1−4x2<br />
dx<br />
∫ √x2<br />
∫ √<br />
9x2 −4<br />
7. +16dx 8. dx<br />
x<br />
∫<br />
x 2<br />
∫<br />
9.<br />
(a 2 −x 2 ) dx 10. x<br />
√ 3/2 x2 −7 dx<br />
11.<br />
13.<br />
15.<br />
∫ 3<br />
0<br />
∫ 2/3<br />
∫<br />
0<br />
dx<br />
√<br />
9+x<br />
2<br />
12.<br />
x 3√ 4−9x 2 dx 14.<br />
1<br />
√<br />
9x2 +6x−8 dx<br />
16. ∫<br />
∫ 1<br />
0<br />
x √ x 2 +8dx<br />
∫ √2x−x2<br />
dx<br />
dx<br />
(x 2 +2x+2) 2
MA111: Prepared by Dr.Archara Pacheenburawana 48<br />
17.<br />
∫<br />
e t√ 9−e 2t dt 18.<br />
∫<br />
dx<br />
√<br />
x2 +a 2 dx<br />
Answer to <strong>Exercise</strong> 6.3<br />
√<br />
π<br />
1. + √ 3<br />
− 1 2. − 4−x2 25−x<br />
24 8 4<br />
2x +C 3. − 2<br />
25x<br />
+C 4. ( √ 1 3<br />
)ln<br />
∣<br />
1<br />
5.<br />
3 (x2 +4) 3/2 −4 √ x 2 +4+C 6. 1 4 sin−1 (2x)+ 1x√ 1−4x<br />
2 2 +C<br />
√ 1<br />
7. x√ x<br />
2 2 x<br />
+4+2ln<br />
∣2 + x2 +4<br />
2 ∣ +C 8. √ 9x 2 −4−2sec −1 ( 3x )+C 2<br />
( √ x 2 +3− √ 3)<br />
x<br />
∣ +C<br />
9.<br />
13.<br />
15.<br />
x<br />
√<br />
a2 −x 2 −sin−1( x<br />
a)<br />
+C 10.<br />
√<br />
x2 −7+C 11. ln(1+ √ 2) 12. 1 3 (x2 +4) 3/2 +C<br />
64<br />
1215<br />
14. 1 2 [sin−1 (x−1)+(x−1) √ 2x−x 2 ]+C<br />
1<br />
ln∣ √<br />
∣<br />
3 3x+1+ 9x2 +6x−8 ∣ +C 16.<br />
1<br />
2<br />
[<br />
tan −1 (x−1)+<br />
]<br />
(x+1)<br />
+C<br />
(x 2 +2x+2)<br />
[<br />
1<br />
17. √ 2 e<br />
t<br />
9−e 2t +9sin −1 ( et)]<br />
+C 18. ln(x+ √ x<br />
3 2 +a 2 )+C<br />
<strong>Exercise</strong> 6.4<br />
Evaluate the integral.<br />
∫ ∫<br />
x−5<br />
1.<br />
x 2 −1 dx<br />
2. 6x<br />
x 2 −x+2 dx<br />
∫<br />
∫<br />
x+1<br />
3.<br />
x 2 −x−6 dx 4. −x+5<br />
x 3 −x 2 −2x dx<br />
∫ x 3 ∫<br />
+x+2<br />
−3x−1<br />
5.<br />
x 2 +2x−8 dx 6. x 3 −x dx<br />
∫ ∫<br />
2x+3<br />
7.<br />
(x+2) dx<br />
8. x−1<br />
2 x 3 +4x 2 +4x dx<br />
∫<br />
∫<br />
x+4<br />
x+2<br />
9.<br />
x 3 +3x 2 +2x dx 10. x 3 +x dx<br />
∫ ∫<br />
4x−2<br />
11.<br />
x 4 −1 dx<br />
12. 3x 2 −6<br />
x 2 −x−2 dx<br />
∫<br />
∫<br />
2x+3<br />
x 2<br />
13.<br />
x 2 +2x+1 dx 14. +2x+1<br />
dx<br />
x 3 +x<br />
∫<br />
4x 2 ∫<br />
+3<br />
15.<br />
x 3 +x 2 +x dx 16. 3x 3 +1<br />
x 3 −x 2 +x−1 dx
MA111: Prepared by Dr.Archara Pacheenburawana 49<br />
Answer to <strong>Exercise</strong> 6.4<br />
1. 3ln|x+1|−2ln|x−1|+C 2. 2ln|x+1|+4ln|x−2|+C<br />
3.<br />
1<br />
5 ln|x+2|+ 4 5 ln|x−3|+C 4. 2ln|x+1|+ 1 2 ln|x−2|− 5 2 ln|x|+C<br />
5. 11ln|x+4|+2ln|x−2|+ 1 2 x2 −2x+C<br />
6. ln|x+1|−2ln|x−1|+ln|x|+C 7. 2ln|x+2|−(x+2) −1 +C<br />
1<br />
8. ln|x+2|− 3 4 2 (x+2)−1 − 1 ln|x|+C 9. ln|x+2|−3ln|x+1|+2ln|x|+C<br />
4<br />
10. −ln(x 2 +1)+tan −1 x+2ln|x|+C<br />
11.<br />
3<br />
2 ln|x+1|+ 1 2 ln|x−1|−ln(x2 +1)+tan −1 x+C<br />
12. 3x+ln|x+1|+2ln|x−2|+C 13. 2ln|x+1|−(x+1) −1 +C<br />
14. 2tan −1 x+ln|x|+C 15. 3ln|x|+ 1 2 ln|x2 +x+1|− 7 √<br />
3<br />
tan −1 (2x+1 √<br />
3<br />
)+C<br />
16. 3x+2ln|x−1|+ 1 2 ln(x2 +1)−2tan −1 x+C<br />
<strong>Exercise</strong> 6.5<br />
Determine whether each integral is convergent or divergent. Evaluate those that are convergent.<br />
1.<br />
3.<br />
5.<br />
7.<br />
9.<br />
11.<br />
13.<br />
15.<br />
17.<br />
∫ ∞<br />
1<br />
∫ ∞<br />
0<br />
∫ ∞<br />
−∞<br />
∫ ∞<br />
0<br />
∫ ∞<br />
1<br />
∫ ∞<br />
1<br />
∫ 0<br />
−1<br />
∫ 3<br />
−2<br />
∫ 2<br />
−2<br />
1<br />
(3x+1) 2 dx<br />
e −x dx 4.<br />
xe −x2 dx 6.<br />
cosxdx 8.<br />
lnx<br />
x dx<br />
2. ∫ −1<br />
−∞<br />
∫ ∞<br />
−∞<br />
∫ ∞<br />
0<br />
∫ 1<br />
−∞<br />
10. ∫ ∞<br />
−∞<br />
lnx<br />
x 2 dx 12. ∫ 3<br />
0<br />
1<br />
√ 2−w<br />
dw<br />
x 3 dx<br />
1<br />
(x+2)(x+3) dx<br />
xe 2x dx<br />
x<br />
1+x 2 dx<br />
1<br />
√ x<br />
dx<br />
∫<br />
1<br />
π/4<br />
x dx 14. csc 2 tdt<br />
2<br />
1<br />
x 4 dx<br />
0<br />
∫ π<br />
16. secxdx<br />
∫<br />
1<br />
2<br />
x 2 −1 dx 18. z 2 lnzdz<br />
0<br />
0
MA111: Prepared by Dr.Archara Pacheenburawana 50<br />
Answer to <strong>Exercise</strong> 6.5<br />
1.<br />
1<br />
2<br />
2. D 3. 1 4. D 5. 0 6. −ln 2 3<br />
7. D 8. e2 4<br />
9. D 10. D 11. 1<br />
12. 2 √ 3 13. D 14. D 15. D 16. D 17. D 18. 8 3 ln2− 8 9<br />
<strong>Exercise</strong> 7.1<br />
1. List the first five terms of the sequence.<br />
(a) a n = 1−(0.2) n (b) a n = n+1<br />
3n−1<br />
(c) a n = 3(−1)n<br />
(e)<br />
{<br />
sin nπ 2<br />
n!<br />
}<br />
(d) {2·4·6·····(2n)}<br />
(f) a 1 = 1, a n = 1<br />
1+a n<br />
2. Findaformulaforthegeneraltermterma n ofthesequence, assuming thatthepattern<br />
of the first few terms continuous.<br />
(a) { 1<br />
2 , 1 4 , 1 8 , 1<br />
16 ,...} (b) { 1<br />
2 , 1 4 , 1 6 , 1 8 ,...}<br />
(c) {2,7,12,17,...} (d) { − 1 4 , 2 9 ,− 3<br />
16 , 4 25 ,...}<br />
(e) { 1,− 2 3 , 4 9 ,− 8<br />
27 ,...} (f) {0,2,0,2,0,2,...}<br />
3. Determine whether the sequence converges of diverges. If it converges, find the limit.<br />
(a) a n = n(n−1) (b) a n = n+1<br />
3n−1 √<br />
(c) a n = 3+5n2<br />
n<br />
(d) a<br />
n+n 2 n =<br />
1+ √ n<br />
(e) a n = 2n<br />
3 n+1 (f) a n =<br />
(g) a n = (−1)n−1 n<br />
n 2 +1<br />
(i) a n = 2+cosnπ<br />
{ } 3+(−1)<br />
n<br />
(k)<br />
n<br />
{ 2 } ln(n 2 )<br />
(m)<br />
n<br />
(o) { √ n+2− √ n}<br />
n<br />
1+ √ n<br />
(h) a n = sin(nπ/2)<br />
(j) {arctan2n}<br />
{ } n!<br />
(l)<br />
(n+2)!<br />
(n) {(−1) n sin(1/n)}<br />
{ } ln(2+e n )<br />
(p)<br />
3n<br />
(q) a n = n2 −n<br />
(r) a n = ln(n+1)−lnn
MA111: Prepared by Dr.Archara Pacheenburawana 51<br />
(s) a n = cos2 n<br />
2 n (t) a n = (1+3n) 1/n<br />
(u) a n = 1 n + 2 2 n +···+ n (v) a 2 n 2<br />
n = ncosn<br />
n 2 +1<br />
(w) a n = n!<br />
(x) a<br />
2 n n = (−3)n<br />
n!<br />
Answer to Selected <strong>Exercise</strong> 7.1<br />
1. (a) 0.8,0.96,0.992,0.9984,0.99968 (c) −3, 3 2 ,−1, 1,− 1 (e) {1,0,−1,0,1,...}<br />
2 8 40<br />
2. (a) a n = 1/2 n (c) 5n−3 (e) ( − 2 3<br />
) n−1<br />
3. (a) D (c) 5 (e) 0 (g) 0 (i) D (k) 0 (m) 0 (o) 0 (q) 0 (s) 0 (u) 1 2<br />
(w) D<br />
<strong>Exercise</strong> 7.2<br />
Determine whether the series is convergent or divergent. If it is convergent, find its sum.<br />
1. 4+ 8 + 16 + 32 +··· 2. −2+ 5 − 25 + 125 −···<br />
5 25 125 2 8 32<br />
∞∑<br />
3. 5 ( 2 n−1<br />
∞∑ (−3)<br />
3) n−1<br />
4.<br />
5.<br />
7.<br />
9.<br />
11.<br />
13.<br />
15.<br />
17.<br />
n=1<br />
∞∑<br />
3 −n 8 n+1 6.<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
1<br />
n(n+2)<br />
n<br />
√<br />
1+n<br />
2<br />
8.<br />
10.<br />
∞∑<br />
arctann 12.<br />
n=1<br />
∞∑ [ (<br />
2<br />
1<br />
) n ( )<br />
4 +3 −<br />
1 n ]<br />
5<br />
n=1<br />
14.<br />
∞∑<br />
( 1<br />
n − 1 )<br />
n−1<br />
16.<br />
∞∑ ( e<br />
) n+1<br />
π<br />
18.<br />
n=2<br />
n=1<br />
n=1<br />
n=1<br />
4 n<br />
∞∑ n<br />
n+5<br />
∞∑<br />
[2(0.1) n +(0.2) n ]<br />
n=1<br />
∞∑ 3 n +2 n<br />
n=1<br />
6 n<br />
∞∑ n<br />
ln<br />
n+1<br />
n=1<br />
∞∑ n−5<br />
n+2<br />
n=1<br />
∞∑ n!<br />
100 n<br />
n=1<br />
∞∑<br />
(<br />
3<br />
(n−1) − 3 )<br />
2 n 2<br />
n=2
MA111: Prepared by Dr.Archara Pacheenburawana 52<br />
Answer to <strong>Exercise</strong> 7.2<br />
1.<br />
20<br />
3<br />
2. D 3. 15 4. 1 7<br />
5. D 6. D 7. 3 4<br />
8. 17<br />
36<br />
9. D 10. 3 2<br />
11. D 12. D<br />
13.<br />
31<br />
6<br />
14. D 15. −1 16. D 17.<br />
e 2<br />
π(π−e)<br />
18. 3<br />
n=1<br />
<strong>Exercise</strong> 7.3<br />
Determine whether the series converges or diverges.<br />
∞∑ 1<br />
∞∑ 1<br />
∞∑<br />
1.<br />
2.<br />
3. ne −n<br />
n 4 3n+1<br />
n=1<br />
n=1<br />
n=1<br />
∞∑ 1<br />
4.<br />
5. 1+ 1 n 1.0001 8 + 1 27 + 1<br />
64 +··· 6. ∑ ∞<br />
5−2 √ n<br />
n 3<br />
n=5<br />
n=1<br />
∞∑<br />
∞∑ n<br />
∞∑ 1<br />
7. ne −n2 8.<br />
9.<br />
n 2 +1<br />
nlnn<br />
n=1<br />
n=1<br />
n=2<br />
∞∑ arctann<br />
∞∑ 1<br />
∞∑ −2<br />
10.<br />
11.<br />
12. √<br />
1+n 2 n 2 +2n+2 n+2<br />
13.<br />
16.<br />
19.<br />
22.<br />
25.<br />
28.<br />
31.<br />
34.<br />
37.<br />
40.<br />
∞∑<br />
n=2<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
7<br />
4n+2<br />
1<br />
n 2 +n+1<br />
14.<br />
17.<br />
3<br />
n2 n 20.<br />
3+cosn<br />
3 n 23.<br />
1<br />
1+ √ n<br />
26.<br />
n+1<br />
n2 n 29.<br />
n<br />
n 2 +2n+3<br />
32.<br />
n!<br />
n 100 35.<br />
n+3<br />
n 2√ n<br />
1<br />
(2n)!<br />
38.<br />
41.<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
3<br />
(4+3n) 7/6 15.<br />
5<br />
2+3 n 18.<br />
1<br />
√<br />
n(n+1)(n+2)<br />
21.<br />
n<br />
√<br />
n5 +4<br />
n 2 +1<br />
n 4 +1<br />
1<br />
n!<br />
1<br />
n √ n+1<br />
n 3<br />
(2n)!<br />
n 2<br />
n!<br />
24.<br />
27.<br />
30.<br />
33.<br />
36.<br />
39.<br />
sin2n<br />
n 2 42.<br />
n=1<br />
∞∑<br />
n=2<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
ne −3n2<br />
n+1<br />
n 2<br />
n 2 +1<br />
n 3 −1<br />
2 n<br />
1+3 n<br />
1+n+n 2<br />
√<br />
1+n2 +n 6<br />
( 1<br />
sin<br />
n)<br />
8 n<br />
n!<br />
n<br />
n+200<br />
4n 3 +3n<br />
n 5 −4n 2 +1<br />
n(−3) n<br />
4 n−1
MA111: Prepared by Dr.Archara Pacheenburawana 53<br />
43.<br />
46.<br />
49.<br />
52.<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
10 n<br />
(n+1)4 2n+1 44.<br />
n n<br />
3 1+3n 47.<br />
n n<br />
(2n)!<br />
50.<br />
∞∑ n!<br />
(−10) n 45.<br />
∞∑<br />
( ) n 2 n<br />
+1<br />
2n 2 +1<br />
48.<br />
∞∑ 4 n +n<br />
n!<br />
51.<br />
n=1<br />
n=1<br />
n=1<br />
∞∑ cos(nπ/3)<br />
n!<br />
∞∑ 1<br />
2+sin 2 n<br />
∞∑<br />
( n<br />
3n+2<br />
1<br />
1·2 + 1<br />
2·3 + 1<br />
3·4 + 1<br />
4·5 +··· 53. 1 3 + 2 3 2 + 3 3 3 + 4 3 4 +···<br />
54. 1+ 1<br />
2 √ 2 + 1<br />
3 √ 3 + 1<br />
4 √ 4 +··· 55. ∞<br />
∑<br />
56.<br />
2<br />
1·3·4 + 3<br />
2·4·5 + 4<br />
3·5·6 + 5<br />
4·6·7 +···<br />
n=1<br />
Answer to <strong>Exercise</strong> 7.3<br />
n=1<br />
n=1<br />
n=1<br />
2·4·6·····(2n)<br />
n!<br />
1. C 2. D 3. C 4. C 5. C 6. C 7. C 8. D 9. D 10. C 11. C 12. D<br />
13. D 14. C 15. C 16. C 17. C 18. D 19. C 20. C 21. D 22. C 23. C<br />
24. C 25. D 26. C 27. D 28. C 29. C 30. D 31. D 32. C 33. C 34. D<br />
35. C 36. D 37. C 38. C 39. C 40. C 41. C 42. C 43. C 44. D 45. C<br />
46. D 47. C 48. C 49. C 50. C 51. C 52. C 53. C 54. C 55. D 56. C<br />
<strong>Exercise</strong> 7.4<br />
1. Find the Maclaurin series for the function.<br />
(a) e −x (b) e ax (c) cosπx<br />
(d) sinπx (e) ln(1+x)<br />
1<br />
(f)<br />
1+x<br />
(g) coshx (h) sinhx (i) xsinx<br />
(j) xe x<br />
2. Find the Taylor series of the function f(x) centered at the given value of a.<br />
(a) e x ; a = 1 (b) e −x ; a = ln2 (c) 1 x ; a = −1<br />
1<br />
(d)<br />
x+2 ; a = 3 (e) sinπx; a = 1 (f) cosx; a = π 2<br />
2<br />
(g) lnx; a = 1<br />
(h) lnx; a = e<br />
) n
MA111: Prepared by Dr.Archara Pacheenburawana 54<br />
1. (a)<br />
(i)<br />
2. (a)<br />
(g)<br />
∞∑ (−1) n<br />
x n (c)<br />
n!<br />
n=0<br />
∞∑<br />
n=0<br />
∞∑<br />
n=0<br />
(−1) n<br />
(2n+1)! x2n+2<br />
e<br />
n! (x−1)n (c)<br />
Answer to Selected <strong>Exercise</strong> 7.4<br />
∞∑ (−1) n π 2k<br />
x 2n (e)<br />
(2n)!<br />
n=0<br />
∞∑ (−1) n−1<br />
(x−1) n<br />
n<br />
n=0<br />
∞∑<br />
(−1)(x+1) n (e)<br />
n=0<br />
∞∑ (−1) n+1<br />
x n (g)<br />
n<br />
n=0<br />
∞∑ (−1) n π 2n<br />
n=0<br />
(2n)!<br />
∞∑<br />
n=0<br />
(<br />
x− 1 ) 2n<br />
2<br />
1<br />
(2n)! x2n