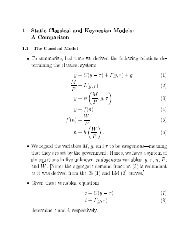Quantile Regression: A Gentle Introduction
Quantile Regression: A Gentle Introduction
Quantile Regression: A Gentle Introduction
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
<strong>Quantile</strong> <strong>Regression</strong>: A <strong>Gentle</strong> <strong>Introduction</strong><br />
Roger Koenker<br />
University of Illinois, Urbana-Champaign<br />
5th RMetrics Workshop, Meielisalp: 28 June 2011<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 1 / 58
Overview of the Course<br />
Some Basics: What, Why and How<br />
Inference and <strong>Quantile</strong> Treatment Effects<br />
Nonparametric <strong>Quantile</strong> <strong>Regression</strong><br />
<strong>Quantile</strong> Autoregression<br />
Risk Assessment and Choquet Portfolios<br />
Course outline, lecture slides, an R FAQ, and even some proposed exercises<br />
can all be found at:<br />
http://www.econ.uiuc.edu/~roger/courses/RMetrics.<br />
A somewhat more extensive set of lecture slides can be found at:<br />
http://www.econ.uiuc.edu/~roger/courses/LSE.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 2 / 58
Boxplots of CEO Pay<br />
annual compensation in millions<br />
0.1 1 10 100<br />
*<br />
+<br />
*<br />
* *<br />
* *<br />
*<br />
+ + + + + +<br />
*<br />
+<br />
*<br />
+<br />
*<br />
+<br />
●<br />
●<br />
●<br />
●<br />
0.1 1 10 100<br />
firm market value in billions<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 3 / 58
Motivation<br />
What the regression curve does is give a grand summary for the<br />
averages of the distributions corresponding to the set of of x’s.<br />
We could go further and compute several different regression<br />
curves corresponding to the various percentage points of the<br />
distributions and thus get a more complete picture of the set.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 4 / 58
Motivation<br />
What the regression curve does is give a grand summary for the<br />
averages of the distributions corresponding to the set of of x’s.<br />
We could go further and compute several different regression<br />
curves corresponding to the various percentage points of the<br />
distributions and thus get a more complete picture of the set.<br />
Ordinarily this is not done, and so regression often gives a rather<br />
incomplete picture.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 4 / 58
Motivation<br />
What the regression curve does is give a grand summary for the<br />
averages of the distributions corresponding to the set of of x’s.<br />
We could go further and compute several different regression<br />
curves corresponding to the various percentage points of the<br />
distributions and thus get a more complete picture of the set.<br />
Ordinarily this is not done, and so regression often gives a rather<br />
incomplete picture. Just as the mean gives an incomplete picture<br />
of a single distribution, so the regression curve gives a<br />
correspondingly incomplete picture for a set of distributions.<br />
Mosteller and Tukey (1977)<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 4 / 58
Motivation<br />
Francis Galton in a famous passage defending the “charms of statistics”<br />
against its many detractors, chided his statistical colleagues<br />
[who] limited their inquiries to Averages, and do not seem to<br />
revel in more comprehensive views. Their souls seem as dull to<br />
the charm of variety as that of a native of one of our flat English<br />
counties, whose retrospect of Switzerland was that, if the<br />
mountains could be thrown into its lakes, two nuisances would<br />
be got rid of at once. Natural Inheritance, 1889<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 5 / 58
Univariate <strong>Quantile</strong>s<br />
Given a real-valued random variable, X, with distribution function F, we<br />
define the τth quantile of X as<br />
Q X (τ) = F −1<br />
X<br />
(τ) = inf{x | F(x) τ}.<br />
This definition follows the usual convention that F is CADLAG, and Q is<br />
CAGLAD as illustrated in the following pair of pictures.<br />
F(x)<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Q(τ)<br />
0.0 1.0 2.0 3.0<br />
0.0 1.0 2.0 3.0<br />
x<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
τ<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 6 / 58
Univariate <strong>Quantile</strong>s<br />
Given a real-valued random variable, X, with distribution function F, we<br />
will define the τth quantile of X as<br />
Q X (τ) = F −1<br />
X<br />
(τ) = inf{x | F(x) τ}.<br />
This definition follows the usual convention that F is CADLAG, and Q is<br />
CAGLAD as illustrated in the following pair of pictures.<br />
F's are CADLAG<br />
Q's are CAGLAD<br />
F(x)<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
●<br />
●<br />
●<br />
●<br />
Q(τ)<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
●<br />
●<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
x<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
τ<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 7 / 58
Univariate <strong>Quantile</strong>s<br />
Viewed from the perspective of densities, the τth quantile splits the area<br />
under the density into two parts: one with area τ below the τth quantile<br />
and the other with area 1 − τ above it:<br />
f(x)<br />
0.0 0.4 0.8<br />
τ<br />
1 − τ<br />
0.0 0.5 1.0 1.5 2.0 2.5 3.0<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 8 / 58
Two Bits Worth of Convex Analysis<br />
A convex function ρ and its subgradient ψ:<br />
ρ τ (u)<br />
τ<br />
ψ τ (u)<br />
τ − 1<br />
τ<br />
τ − 1<br />
The subgradient of a convex function f(u) at a point u consists of all the<br />
possible “tangents.” Sums of convex functions are convex.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 9 / 58
Population <strong>Quantile</strong>s as Optimizers<br />
<strong>Quantile</strong>s solve a simple optimization problem:<br />
ˆα(τ) = argmin E ρ τ (Y − α)<br />
Proof: Let ψ τ (u) = ρ ′ τ(u), so differentiating wrt to α:<br />
0 =<br />
∫ ∞<br />
−∞<br />
ψ τ (y − α)dF(y)<br />
= (τ − 1)<br />
∫ α<br />
dF(y) + τ<br />
−∞<br />
∫ ∞<br />
α<br />
dF(y)<br />
= (τ − 1)F(α) + τ(1 − F(α))<br />
implying τ = F(α) and thus ˆα = F −1 (τ).<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 10 / 58
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
Sample <strong>Quantile</strong>s as Optimizers<br />
For sample quantiles replace F by ˆF, the empirical distribution function.<br />
The objective function becomes a polyhedral convex function whose<br />
derivative is monotone decreasing, in effect the gradient simply counts<br />
observations above and below and weights the sums by τ and 1 − τ.<br />
R(x)<br />
20 30 40 50 60 70 80<br />
● ●●<br />
● ●<br />
●●●● ●●<br />
● ●<br />
R'(x)<br />
−15 −10 −5 0 5 10 15<br />
−2 0 2 4<br />
x<br />
−2 0 2 4<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 11 / 58
Conditional <strong>Quantile</strong>s: The Least Squares Meta-Model<br />
The unconditional mean solves<br />
µ = argmin m E(Y − m) 2<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 12 / 58
Conditional <strong>Quantile</strong>s: The Least Squares Meta-Model<br />
The unconditional mean solves<br />
µ = argmin m E(Y − m) 2<br />
The conditional mean µ(x) = E(Y|X = x) solves<br />
µ(x) = argmin m E Y|X=x (Y − m(X)) 2 .<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 12 / 58
Conditional <strong>Quantile</strong>s: The Least Squares Meta-Model<br />
The unconditional mean solves<br />
µ = argmin m E(Y − m) 2<br />
The conditional mean µ(x) = E(Y|X = x) solves<br />
µ(x) = argmin m E Y|X=x (Y − m(X)) 2 .<br />
Similarly, the unconditional τth quantile solves<br />
α τ = argmin a Eρ τ (Y − a)<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 12 / 58
Conditional <strong>Quantile</strong>s: The Least Squares Meta-Model<br />
The unconditional mean solves<br />
µ = argmin m E(Y − m) 2<br />
The conditional mean µ(x) = E(Y|X = x) solves<br />
µ(x) = argmin m E Y|X=x (Y − m(X)) 2 .<br />
Similarly, the unconditional τth quantile solves<br />
α τ = argmin a Eρ τ (Y − a)<br />
and the conditional τth quantile solves<br />
α τ (x) = argmin a E Y|X=x ρ τ (Y − a(X))<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 12 / 58
Computation of Linear <strong>Regression</strong> <strong>Quantile</strong>s<br />
Primal Formulation as a linear program, split the residual vector into<br />
positive and negative parts and sum with appropriate weights:<br />
min{τ1 ⊤ u + (1 − τ)1 ⊤ v|y = Xb + u − v, (b, u, v) ∈ |R p × |R 2n<br />
+ }<br />
Dual Formulation as a Linear Program<br />
max{y ′ d|X ⊤ d = (1 − τ)X ⊤ 1, d ∈ [0, 1] n }<br />
Solutions are characterized by an exact fit to p observations.<br />
Let h ∈ H index p-element subsets of {1, 2, ..., n} then primal solutions<br />
take the form:<br />
ˆβ = ˆβ(h) = X(h) −1 y(h)<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 13 / 58
Least Squares from the <strong>Quantile</strong> <strong>Regression</strong> Perspective<br />
Exact fits to p observations:<br />
ˆβ = ˆβ(h) = X(h) −1 y(h)<br />
OLS is a weighted average of these ˆβ(h)’s:<br />
ˆβ OLS = (X ⊤ X) −1 X ⊤ y = ∑ h∈H<br />
w(h)ˆβ(h),<br />
w(h) = |X(h)| 2 / ∑ h∈H<br />
|X(h)| 2<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 14 / 58
Least Squares from the <strong>Quantile</strong> <strong>Regression</strong> Perspective<br />
Exact fits to p observations:<br />
ˆβ = ˆβ(h) = X(h) −1 y(h)<br />
OLS is a weighted average of these ˆβ(h)’s:<br />
ˆβ OLS = (X ⊤ X) −1 X ⊤ y = ∑ h∈H<br />
w(h)ˆβ(h),<br />
w(h) = |X(h)| 2 / ∑ h∈H<br />
|X(h)| 2<br />
The determinants |X(h)| are the (signed) volumes of the parallelipipeds<br />
formed by the columns of the the matrices X(h). In the simplest bivariate<br />
case, we have,<br />
|X(h)| 2 =<br />
∣ 1 x ∣<br />
i ∣∣∣<br />
2<br />
= (x<br />
1 x j − x i ) 2<br />
j<br />
so pairs of observations that are far apart are given more weight.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 14 / 58
<strong>Quantile</strong> <strong>Regression</strong>: The Movie<br />
Bivariate linear model with iid Student t errors<br />
Conditional quantile functions are parallel in blue<br />
100 observations indicated in blue<br />
Fitted quantile regression lines in red.<br />
Intervals for τ ∈ (0, 1) for which the solution is optimal.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 15 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.069 , 0.096 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 16 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.138 , 0.151 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 17 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.231 , 0.24 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 18 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.3 , 0.3 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 19 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.374 , 0.391 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 20 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.462 , 0.476 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 21 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.549 , 0.551 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 22 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.619 , 0.636 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 23 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.704 , 0.729 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 24 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.768 , 0.798 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 25 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the iid Error Model<br />
y<br />
−2 0 2 4 6 8 10 12<br />
[ 0.919 , 0.944 ]<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 26 / 58
Virtual <strong>Quantile</strong> <strong>Regression</strong> II<br />
Bivariate quadratic model with Heteroscedastic χ 2 errors<br />
Conditional quantile functions drawn in blue<br />
100 observations indicated in blue<br />
Fitted quadratic quantile regression lines in red<br />
Intervals of optimality for τ ∈ (0, 1).<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 27 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.048 , 0.062 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 28 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.179 , 0.204 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 29 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.261 , 0.261 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 30 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.304 , 0.319 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 31 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.414 , 0.417 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 32 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.499 , 0.507 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 33 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.581 , 0.582 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 34 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.633 , 0.635 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 35 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.685 , 0.685 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 36 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.73 , 0.733 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 37 / 58
<strong>Quantile</strong> <strong>Regression</strong> in the Heteroscedastic Error Model<br />
y<br />
0 20 40 60 80 100<br />
●<br />
●●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ● ●<br />
● ● ●<br />
●●<br />
●<br />
● ● ●<br />
[ 0.916 , 0.925 ]<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 38 / 58
Conditional Means vs. Medians<br />
●<br />
y<br />
0 10 20 30 40<br />
●<br />
● ●<br />
●<br />
mean<br />
median<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
0 2 4 6 8 10<br />
x<br />
Minimizing absolute errors for median regression can yield something quite<br />
different from the least squares fit for mean regression.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 39 / 58
Equivariance of <strong>Regression</strong> <strong>Quantile</strong>s<br />
Scale Equivariance: For any a > 0, ˆβ(τ; ay, X) = aˆβ(τ; y, X) and<br />
ˆβ(τ; −ay, X) = aˆβ(1 − τ; y, X)<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 40 / 58
Equivariance of <strong>Regression</strong> <strong>Quantile</strong>s<br />
Scale Equivariance: For any a > 0, ˆβ(τ; ay, X) = aˆβ(τ; y, X) and<br />
ˆβ(τ; −ay, X) = aˆβ(1 − τ; y, X)<br />
<strong>Regression</strong> Shift: For any γ ∈ |R p ˆβ(τ; y + Xγ, X) = ˆβ(τ; y, X) + γ<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 40 / 58
Equivariance of <strong>Regression</strong> <strong>Quantile</strong>s<br />
Scale Equivariance: For any a > 0, ˆβ(τ; ay, X) = aˆβ(τ; y, X) and<br />
ˆβ(τ; −ay, X) = aˆβ(1 − τ; y, X)<br />
<strong>Regression</strong> Shift: For any γ ∈ |R p ˆβ(τ; y + Xγ, X) = ˆβ(τ; y, X) + γ<br />
Reparameterization of Design: For any |A| ≠ 0,<br />
ˆβ(τ; y, AX) = A −1 ˆβ(τ; yX)<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 40 / 58
Equivariance of <strong>Regression</strong> <strong>Quantile</strong>s<br />
Scale Equivariance: For any a > 0, ˆβ(τ; ay, X) = aˆβ(τ; y, X) and<br />
ˆβ(τ; −ay, X) = aˆβ(1 − τ; y, X)<br />
<strong>Regression</strong> Shift: For any γ ∈ |R p ˆβ(τ; y + Xγ, X) = ˆβ(τ; y, X) + γ<br />
Reparameterization of Design: For any |A| ≠ 0,<br />
ˆβ(τ; y, AX) = A −1 ˆβ(τ; yX)<br />
Robustness: For any diagonal matrix D with nonnegative elements.<br />
ˆβ(τ; y, X) = ˆβ(τ, y + Dû, X)<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 40 / 58
Equivariance to Monotone Transformations<br />
For any monotone function h, conditional quantile functions Q Y (τ|x) are<br />
equivariant in the sense that<br />
Q h(Y)|X (τ|x) = h(Q Y|X (τ|x))<br />
In contrast to conditional mean functions for which, generally,<br />
E(h(Y)|X) ≠ h(EY|X)<br />
Examples:<br />
h(y) = min{0, y}, Powell’s (1985) censored regression estimator.<br />
h(y) = sgn{y} Rosenblatt’s (1957) perceptron, Manski’s (1975) maximum<br />
score estimator. estimator.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 41 / 58
Beyond Average Treatment Effects<br />
Lehmann (1974) proposed the following general model of treatment<br />
response:<br />
“Suppose the treatment adds the amount ∆(x) when the<br />
response of the untreated subject would be x. Then the<br />
distribution G of the treatment responses is that of the random<br />
variable X + ∆(X) where X is distributed according to F.”<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 42 / 58
Lehmann QTE as a QQ-Plot<br />
Doksum (1974) defines ∆(x) as the “horizontal distance” between F and<br />
G at x, i.e.<br />
F(x) = G(x + ∆(x)).<br />
Then ∆(x) is uniquely defined as<br />
∆(x) = G −1 (F(x)) − x.<br />
This is the essence of the conventional QQ-plot. Changing variables so<br />
τ = F(x) we have the quantile treatment effect (QTE):<br />
δ(τ) = ∆(F −1 (τ)) = G −1 (τ) − F −1 (τ).<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 43 / 58
Lehmann-Doksum QTE<br />
P<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
F<br />
G<br />
−4 −2 0 2 4<br />
x<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 44 / 58
Lehmann-Doksum QTE<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
P<br />
Location Shift<br />
−6 −4 −2 0 2 4 6<br />
x<br />
density<br />
0.0 0.1 0.2 0.3 0.4<br />
−6 −4 −2 0 2 4 6<br />
x<br />
QTE<br />
0.990 1.000 1.010<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
P<br />
Scale Shift<br />
−6 −4 −2 0 2 4 6<br />
x<br />
0.0 0.1 0.2 0.3 0.4<br />
−6 −4 −2 0 2 4 6<br />
x<br />
QTE<br />
−2 −1 0 1 2<br />
density<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
P<br />
Location and Scale Shift<br />
−6 −4 −2 0 2 4 6<br />
x<br />
0.0 0.1 0.2 0.3 0.4<br />
−6 −4 −2 0 2 4 6<br />
x<br />
QTE<br />
−1 0 1 2 3<br />
density<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
u<br />
u<br />
u<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 45 / 58
An Asymmetric Example<br />
P<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
density<br />
0.0 0.1 0.2 0.3 0.4 0.5 0.6<br />
QTE<br />
−10 −5 0 5 10<br />
0 2 4 6 8 10 12<br />
x<br />
0 2 4 6 8 10 12<br />
x<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
u<br />
Treatment shifts the distribution from right skewed to left skewed making<br />
the QTE U-shaped.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 46 / 58
QTE via <strong>Quantile</strong> <strong>Regression</strong><br />
The Lehmann QTE is naturally estimable by<br />
ˆδ(τ) = Ĝ −1<br />
n (τ) − ˆF −1<br />
m (τ)<br />
where Ĝ n and ˆF m denote the empirical distribution functions of the<br />
treatment and control observations, Consider the quantile regression model<br />
Q Yi (τ|D i ) = α(τ) + δ(τ)D i<br />
where D i denotes the treatment indicator, and Y i = h(T i ), e.g.<br />
Y i = log T i , which can be estimated by solving,<br />
min<br />
n∑<br />
ρ τ (y i − α − δD i )<br />
i=1<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 47 / 58
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ●<br />
●<br />
● ● ●<br />
●<br />
●<br />
● ● ● ●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●●<br />
●<br />
●<br />
● ●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
● ●<br />
● ●<br />
● ●<br />
●<br />
● ●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●● ●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
Engel’s Food Expenditure Data<br />
Food Expenditure<br />
500 1000 1500 2000<br />
● ●<br />
● ●<br />
● ●<br />
1000 2000 3000 4000 5000<br />
Household Income<br />
Engel Curves for Food: This figure plots data taken from Engel’s (1857) study of the dependence<br />
of households’ food expenditure on household income. Seven estimated quantile<br />
regression lines for τ ∈ {.05, .1, .25, .5, .75, .9, .95} are superimposed on the scatterplot.<br />
The median τ = .5 fit is indicated by the blue solid line; the least squares estimate of the<br />
conditional mean function is indicated by the red dashed line.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 48 / 58
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
Engel’s Food Expenditure Data<br />
Food Expenditure<br />
300 400 500 600 700 800<br />
● ●<br />
400 500 600 700 800 900 1000<br />
Household Income<br />
Engel Curves for Food: This figure plots data taken from Engel’s (1857) study of the dependence<br />
of households’ food expenditure on household income. Seven estimated quantile<br />
regression lines for τ ∈ {.05, .1, .25, .5, .75, .9, .95} are superimposed on the scatterplot.<br />
The median τ = .5 fit is indicated by the blue solid line; the least squares estimate of the<br />
conditional mean function is indicated by the red dashed line.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 49 / 58
A Model of Infant Birthweight<br />
Reference: Abrevaya (2001), Koenker and Hallock (2001)<br />
Data: June, 1997, Detailed Natality Data of the US. Live, singleton<br />
births, with mothers recorded as either black or white, between 18-45,<br />
and residing in the U.S. Sample size: 198,377.<br />
Response: Infant Birthweight (in grams)<br />
Covariates:<br />
◮ Mother’s Education<br />
◮ Mother’s Prenatal Care<br />
◮ Mother’s Smoking<br />
◮ Mother’s Age<br />
◮ Mother’s Weight Gain<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 50 / 58
<strong>Quantile</strong> <strong>Regression</strong> Birthweight Model I<br />
Intercept<br />
Boy<br />
Married<br />
Black<br />
2500 3000 3500 4000<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
•<br />
•<br />
•<br />
40 60 80 100 120 140<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
40 60 80 100<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
•<br />
• • •<br />
• •<br />
•<br />
•<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
•<br />
•<br />
-350 -300 -250 -200 -150<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
• • •<br />
•<br />
•<br />
• • •<br />
• •<br />
• •<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Mother’s Age<br />
Mother’s Age^2<br />
High School<br />
Some College<br />
30 40 50 60<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
• •<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
-1.0 -0.8 -0.6 -0.4<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
•<br />
• • • •<br />
• • •<br />
•<br />
•<br />
•<br />
• •<br />
0 10 20 30<br />
•<br />
• •<br />
•<br />
•<br />
• • •<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
10 20 30 40 50<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• • •<br />
•<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 51 / 58
<strong>Quantile</strong> <strong>Regression</strong> Birthweight Model II<br />
College<br />
No Prenatal<br />
Prenatal Second<br />
Prenatal Third<br />
-20 0 20 40 60 80 100<br />
•<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
-500 -400 -300 -200 -100 0<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
•<br />
• •<br />
•<br />
•<br />
• • •<br />
• • •<br />
•<br />
•<br />
0 20 40 60<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• • •<br />
• •<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
-50 0 50 100 150<br />
•<br />
•<br />
•<br />
•<br />
• • •<br />
• •<br />
• • •<br />
• •<br />
• • •<br />
•<br />
•<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Smoker<br />
Cigarette’s/Day<br />
Mother’s Weight Gain<br />
Mother’s Weight Gain^2<br />
-200 -180 -160 -140<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
• •<br />
•<br />
-6 -5 -4 -3 -2<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• • •<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
0 10 20 30 40<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
-0.3 -0.2 -0.1 0.0 0.1<br />
•<br />
•<br />
•<br />
•<br />
•<br />
• •<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
•<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 52 / 58
Marginal Effect of Mother’s Age<br />
Weight Gain Effect<br />
0.01 0.03 0.05<br />
● ●<br />
●<br />
●<br />
●<br />
●<br />
Weight Gain Effect<br />
0.01 0.02 0.03 0.04<br />
●<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●<br />
● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●<br />
0.0 0.2 0.4 0.6 0.8<br />
0.0 0.2 0.4 0.6 0.8<br />
<strong>Quantile</strong><br />
<strong>Quantile</strong><br />
●<br />
●<br />
Weight Gain Effect<br />
0.010 0.015 0.020<br />
●<br />
●<br />
●<br />
●<br />
●<br />
● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●<br />
Weight Gain Effect<br />
0.007 0.009 0.011<br />
● ●<br />
●<br />
●<br />
●<br />
● ● ● ●<br />
● ● ● ● ● ● ● ● ● ● ●<br />
● 0.0 0.2 0.4 0.6 0.8<br />
0.0 0.2 0.4 0.6 0.8<br />
<strong>Quantile</strong><br />
<strong>Quantile</strong><br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 53 / 58
Marginal Effect of Mother’s Weight Gain<br />
Weight Gain Effect<br />
0.4 0.5 0.6 0.7<br />
Weight Gain Effect<br />
0.45 0.55 0.65<br />
20 25 30 35 40 45<br />
20 25 30 35 40 45<br />
Mother's Age<br />
Mother's Age<br />
Weight Gain Effect<br />
0.44 0.48 0.52 0.56<br />
Weight Gain Effect<br />
0.45 0.50 0.55 0.60<br />
20 25 30 35 40 45<br />
20 25 30 35 40 45<br />
Mother's Age<br />
Mother's Age<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 54 / 58
Daily Temperature in Melbourne: AR(1) Scatterplot<br />
today's max temperature<br />
10 20 30 40<br />
10 15 20 25 30 35 40<br />
yesterday's max temperature<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 55 / 58
Daily Temperature in Melbourne: Nonlinear QAR(1) Fit<br />
today's max temperature<br />
10 20 30 40<br />
10 15 20 25 30 35 40<br />
yesterday's max temperature<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 56 / 58
Conditional Densities of Melbourne Daily Temperature<br />
Yesterday's Temp 11<br />
Yesterday's Temp 16<br />
Yesterday's Temp 21<br />
density<br />
0.05 0.15<br />
density<br />
0.00 0.05 0.10 0.15<br />
density<br />
0.02 0.06 0.10<br />
10 12 14 16 18<br />
12 16 20 24<br />
15 20 25 30<br />
today's max temperature<br />
today's max temperature<br />
today's max temperature<br />
Yesterday's Temp 25<br />
Yesterday's Temp 30<br />
Yesterday's Temp 35<br />
density<br />
0.01 0.03 0.05 0.07<br />
density<br />
0.01 0.03 0.05 0.07<br />
density<br />
0.01 0.03 0.05 0.07<br />
15 20 25 30 35<br />
20 25 30 35<br />
20 25 30 35 40<br />
today's max temperature<br />
today's max temperature<br />
today's max temperature<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 57 / 58
Review<br />
Least squares methods of estimating conditional mean functions<br />
were developed for, and<br />
promote the view that,<br />
Response = Signal + iid (Gaussian Measurement Error<br />
In fact the world is rarely this simple. <strong>Quantile</strong> regression is intended to<br />
expand the regression window allowing us to see a wider vista.<br />
Roger Koenker (UIUC) <strong>Introduction</strong> Meielisalp: 28.6.2011 58 / 58