1 PHYS1100 Practice problem set, Chapter 14: 4, 8, 13, 16, 18, 22 ...

PHYS1100 Practice problem set, Chapter 14: 4, 8, 13, 16, 18, 22, 35, 36, 43, 61, 67, 75
14.4. Model: The air-track glider attached to a spring is in simple harmonic motion.
Visualize: The position of the glider can be represented as x(t) = A cos ωt.
Solve: The glider is pulled to the right and released from rest at t = 0 s . It then oscillates with a period T = 2.0 s
and a maximum speed v
max
= 40 cm s = 0.40 m s .
(a)
2 2 v 0.40 m s
v = π π
max
ω A ω = A
T
= π
2.0 s = ⇒ = ω
= π rad s
= =
max
and rad s 0.127 m 12.7 cm
(b) The glider’s position at t = 0.25 s is
( ) ⎡( π )( )
x0.25 s
= 0.127 m cos
⎣
rad s 0.25 s ⎤
⎦
= 0.090 m = 9.0 cm
2
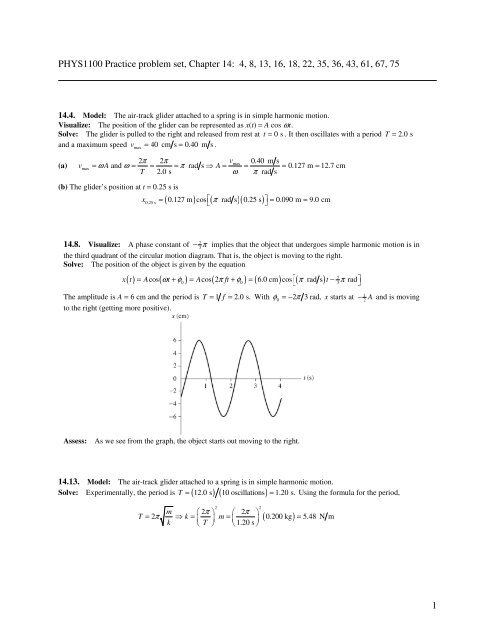
14.8. Visualize: A phase constant of − π 3
implies that the object that undergoes simple harmonic motion is in
the third quadrant of the circular motion diagram. That is, the object is moving to the right.
Solve: The position of the object is given by the equation
2
( ) = ( + ) = ( + ) = ( ) ⎡( ) −
x t Acos ωt φ0 Acos 2π ft φ0 6.0 cm cos
⎣ π rad s t
3
π rad⎤
⎦
1
The amplitude is A = 6 cm and the period is T = 1 f = 2.0 s. With φ0 = − 2π
3 rad, x starts at − A 2
and is moving
to the right (getting more positive).
Assess:
As we see from the graph, the object starts out moving to the right.
14.13. Model: The air-track glider attached to a spring is in simple harmonic motion.
T = 12.0 s 10 oscillations = 1.20 s. Using the formula for the period,
Solve: Experimentally, the period is ( ) ( )
2 2
m ⎛ 2π
⎞ ⎛ 2π
⎞
T = 2π
⇒ k = m
( 0.200 kg)
5.48 N m
k
⎜
T
⎟ = ⎜ =
1.20 s
⎟
⎝ ⎠ ⎝ ⎠
1

14.16. Model: The mass attached to the spring is in simple harmonic motion.
Solve: (a) The period is
( 0.507 kg)
( 20 N m)
m
T = 2π
= 2π
= 1.00 s
k
(b) The angular frequency is ω = 2π T = 2π 1.0 s = 2 π rad s.
(c) To calculate the phase constant φ
0
,
−
( ) ( )
x = Acosφ ⇒ 0.05 m = 0.10 m cosφ ⇒ φ = cos = ± π rad
1 1 1
0 0 0 0 2 3
Because the mass is moving to the right at t = 0 s, it is in the lower half of the circular motion diagram. Hence,
1
φ0 = −
3
π rad.
(d) At t = 0 s, v ( t) ( 0.10 m)( 2 π rad s) sin( 2π t φ )
x
= − + becomes
1
( )( π ) ( π )
0
− 0.10 m 2 rad s sin − rad = 0.544 m s
(e) The maximum speed v ω A ( π )( )
max
= = 2 rad s 0.10 m = 0.628 m s .
x1.3 s
= 0.10 m cos⎡
⎣
2π 1.3 s −
3π
rad⎤
⎦
= 0.0669 m .
(g) At t = 1.3 s, ( ) ( )
1
v π ⎣
⎡ π π
= − 0.10 m 2 rad s sin 2 rad s 1.3 s −
1.3 s 3
rad = −0.467 m s
x
(h) At t = 1.3 s, ( ) ( )( ) ( )( )
1
3
⎦
⎤
.
14.18. Model: The vertical oscillations constitute simple harmonic motion.
Visualize:
Solve: (a) At equilibrium, Newton’s first law applied to the physics book is
( sp )
F − mg = 0 N ⇒ −k∆y − mg = 0 N
y
2
( )( ) ( )
⇒ k = −mg ∆ y = − 0.500 kg 9.8 m s − 0.20 m = 24.5 N m
(b) To calculate the period:
k 24.5 N m 2π
2 π rad
ω = = = 7.0 rad s and T = = = 0.898 s
m 0.50 kg ω 7.0 rad s
(c) The maximum speed is
( )( )
vmax = Aω = 0.10 m 7.0 rad s = 0.70 m s
Maximum speed occurs as the book passes through the equilibrium position.
2

14.22. Model: Assume a small angle of oscillation so there is simple harmonic motion.
Solve: The period of the pendulum is
T
L
π
g
0
0
= 2 = 4.0 s
(a) The period is independent of the mass and depends only on the length. Thus T = T0 = 4.0 s.
(b) For a new length L = 2L 0 ,
(c) For a new length L = L 0 /2,
2L
T = π = =
g
0
2 2T0
5.66 s
L 2 1
T = π = =
g 2
0
2 T0
2.83 s
(d) The period is independent of the amplitude as long as there is simple harmonic motion. Thus T = 4.0 s.
14.35. Model: The vertical mass/spring systems are in simple harmonic motion.
Visualize: Please refer to Figure P14.35.
Solve: (a) For system A, the maximum speed while traveling in the upward direction corresponds to the
maximum positive slope, which is at t = 3.0 s. The frequency of oscillation is 0.25 Hz.
(b) For system B, all the energy is potential energy when the position is at maximum amplitude, which for the first time
is at t = 1.5 s. The time period of system B is thus 6.0 s.
(c) Spring/mass A undergoes three oscillations in 12 s, giving it a period T
A
= 4.0 s. Spring/mass B undergoes 2
oscillations in 12 s, giving it a period T
B
= 6.0 s. We have
If m A = m B , then
T
A
mA mB T ⎛
A
m ⎞⎛
A
k ⎞
B
4.0 s 2
= 2 π and TB
= 2π
⇒ = ⎜ ⎟⎜ ⎟ = =
kA kB TB ⎝ mB ⎠⎝ kA
⎠ 6.0 s 3
k
k
B
A
= ⇒ = =
A
4 k 9
9 k 4
B
2.25
3

14.36. Model: The astronaut attached to the spring is in simple harmonic motion.
Visualize: Please refer to Figure P14.36.
Solve: (a) From the graph, T = 3.0 s, so we have
2 2
m ⎛ T ⎞ ⎛ 3.0 s ⎞
T = 2π
⇒ m = k ( 240 N m)
54.7 kg
k
⎜
2π
⎟ = ⎜ =
2π
⎟
⎝ ⎠ ⎝ ⎠
1
(b) Oscillations occur about an equilibrium position of 1.0 m. From the graph, A ( )
0 rad, and
The equation for the position of the astronaut is
2π
2π
ω = = = 2.094 rad s
T 3.0 s
x( t) A ωt ( ) ⎡
⎣( ) t⎤
⎦
( ) ( ) ( )
= cos + 1.0 m = 0.4 m cos 2.094 rad s + 1.0 m
=
2
0.80 m = 0.40 m, φ0
=
⇒ 1.2 m= 0.4 m cos⎡ ⎣
2.094 rad s t⎤ ⎦
+ 1.0 m ⇒ cos⎡ ⎣
2.094 rad s t⎤
⎦
= 0.5 ⇒ t = 0.50 s
The equation for the velocity of the astronaut is
Thus her speed is 0.725 m/s.
vx
( t) = −Aω
sin( ωt)
( )( ) ⎡( )( )
⇒ v0.5 s
= − 0.4 m 2.094 rad s sin
⎣
2.094 rad s 0.50 s ⎤
⎦
= −0.725 m s
14.43. Model: The ball attached to a spring is in simple harmonic motion.
Solve: (a) Let t = 0 s be the instant when x 0 = −5 cm and v 0 = 20 cm/s. The oscillation frequency is
Using Equation 14.27, the amplitude of the oscillation is
(b) The maximum acceleration is a
ω = k 2.5 N m 5.0 rad/s
m
= 0.10 kg
=
2
2 ⎛ v0
⎞
2 ⎛ 20 cm /s ⎞
A = x0
+ ⎜ ⎟ = ( − 5 cm)
+ ⎜ ⎟ = 6.40 cm
⎝ ω ⎠ ⎝ 5 rad/s ⎠
2 2
max
= ω A = 160 cm s .
(c) For an oscillator, the acceleration is most positive ( a = a max ) when the displacement is most negative
( x = − x = − A)
. So the acceleration is maximum when x = − 6.40 cm .
max
(d) We can use the conservation of energy between x
0
= − 5 cm and x 1 = 3 cm:
( )
1 2 1 2 1 2 1 2 2 2 2
2
mv0 +
2
kx0 =
2
mv1 +
2
kx1 ⇒ v k
1
= v0 + x0 − x1
= 0.283 m s = 28.3 cm s
m
Because k is known in SI units of N/m, the energy calculation must be done using SI units of m, m/s, and kg.
2
4

14.61. Model: A completely inelastic collision between the two gliders resulting in simple harmonic motion.
Visualize:
Let us denote the 250 g and 500 g masses as m 1 and m 2 , which have initial velocities v i1 and v i2 . After m 1 collides
with and sticks to m 2 , the two masses move together with velocity v f .
Solve: The momentum conservation equation pf = pi
for the completely inelastic collision is ( m + m ) v =
m v
+ m v . Substituting the given values,
1 i1 2 i2
( ) v ( )( ) ( )( )
0.750 kg = 0.25 kg 1.20 m s + 0.50 kg 0 m s ⇒ v = 0.40 m s
We now use the conservation of mechanical energy equation:
f
1 1
( ) ( ) ( )
K + U = K + U ⇒ 0 J + kA = m + m v + 0 J
2 2
s compressed
s equilibrium
2 2 1 2 f
m
+ m
k
0.750 kg
( 0.40 m s ) 0.110 m
10 N m
1 2
⇒ A = vf
= =
The period is
m1 + m2 0.750 kg
T = 2π
= 2π
= 1.72 s
k 10 N m
f
1 2 f
5

14.67. Model: Assume that r marble