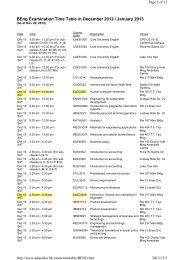
Zeroth Order Bessel Equation

The solution of the zeroth order Bessel’s Equation
Zero Order Bessel Function
Ang Man Shun
October 16, 2012
Is
t 2 d2 y(t)
dt 2 + t d dt y(t) + t2 y = 0
y(t) =
∞∑
k=0
(−1) k
2 2k (k!) 2 · t2k
1 Review of related mathematics
1.1 Binomial Expansion
A special case ,
(a + b) n =
n∑
Cr n a n−r b r
r=0
(1 + x) n =
n∑
Cr n x r
r=0
The binomial coefficient C n r
For n ∈ R and r > 0
C n r =
n!
(n − r)!r!
n, r ∈ Z + n > r
C n r =
n · (n − 1) · (n − 2) ...(n − r + 1)
r!
1

1.2 Laplace Transfrom
Property 1
Pf.
And thus
{ } d
L
dt x(t) =
{ } d 2 x(t)
L
dt 2
ˆ ∞
0
⎧
L {x(t)} =
( d
dt x(t) )
e −st dt =
ˆ ∞
ˆ ∞
0
e −st dx(t) = e −st x(t)| ∞ 0
= −x(0) + s x(t)e −st dt = sX(s) − x(0)
0
} {{ }
⎫
ˆ ∞
X(s)
⎪⎨ ( )
d dx(t)
⎪⎬ { } dx(t)
= L
= s L
dt dt
dt
⎪⎩ } {{ } ⎪⎭ } {{ }
f(t)
F (s)
0
x(t)e −st dt = X(s)
{ } d
L
dt x(t) = sX(s) − x(0)
−
ˆ ∞
0
x(t)de −st
− dx(t) | x=0 = s 2 X(s) − sx(0) − x ′ (0)
dt
Property 2
L {tx(t)} = − d ds X(s)
Pf.
− d ds X(s) = − d ds L {x(t)} = − d ds
ˆ ∞
0
x(t)e −st dt = −
ˆ ∞
x(t) d ds e−st dt = −
ˆ ∞
0
0
x(t)(−t)e −st dt = L {tx(t)}
Property 3
Pf.
L {t n } = n!
s n+1
L { t 0} =L {1}=
ˆ ∞
0
e −st dt = e−st | ∞ 0
−s
= 1 s = 0!
s 1
L { t 1} = L {t · 1}= − d ds L {1} = − d 1
ds s = 1 s = 1!
2 s 2
L { t 2} = L {t · t}= − d ds L {t} = − d 1
ds s = 2 2 s = 2!
3 s 3
Assume L { t k} = k! , then apply property 2 again ,
sk+1 L { t k+1} = L { t · t k} = − d ds L { t k} = − d k! (k + 1)!
=
ds sk+1 s k+2
So the prove by Mathematical Induction is now complete.
2

2 Solving Zeroth Oder Bessel Differential Equation
2.1 General Bessel Differential Eqaution
t 2 d2 y(t)
dt 2
+ t dy(t)
dt
p is called the order of Bessel’s Equation
+ ( t 2 − p 2) y = 0 p ≥ 0
2.2 The solution of p = 0 , Zeroth Order
Divide the equation by t
Apply Laplace Transform
t 2 d2 y(t)
dt 2
+ t dy(t)
dt
ty” + y ′ + ty = 0
+ t 2 y(t) = 0
Apply L-property :
L {ty”} + L {y ′ } + L {ty} = 0
ty” ←→ (−1) 1 dF
ds , d 2
dt y(t) ←→ 2 s2 Y (s) − sy(0) − y ′ (0) and d y(t) ←→ sY (s) −
dt
y(0)
⇒
⇒
− d ds L {y”} + L {y′ } − d ds L {y} = 0
− d ds
{
s 2 Y (s) − sy(0) − y ′ (0) } + {sY (s) − y(0)} − d ds Y (s) = 0
⇒
− d ds s2 Y (s) + d
} {{ } ds sy(0) + d
} {{ } ds y′ (0) +sY (s) − y(0) − d
} {{ }
ds Y (s) = 0
2sY +s 2 Y ′ +y(0) 0
⇒ −2sY − s 2 Y ′ + sY − Y ′ = 0 ⇒ ( s 2 + 1 ) dY (s)
ds
+ sY (s) = 0 ⇒
dY (s)
ds
+ s
s 2 + 1 Y (s) = 0
⇒
dY (s)
Y (s) + s
s 2 + 1 ds = 0 ⇒ ln Y (s) + 1 2 ln ( s 2 + 1 ) = C ′ ⇒ ln Y + ln ( s 2 + 1 ) 1 2
= C
⇒
[
ln Y √ ]
s 2 + 1 = C ′ ⇒ Y (s) =
C
√
s2 + 1
Let C = 1 , and rewrite it into the form
Y (s) = ( s 2 + 1 ) − 1 2
= 1 s
(1 + 1 s 2 ) −
1
2
3

Apply Binomial Expansion
Where
Y (s) = 1 s
∞∑
k=0
C − 1 2
k
( 1
s 2 ) k
=
∞∑
k=0
C − 1 2
k
1
s 2k+1
C −1
2
k
=
(
− 1 ) ( −1
2
2 − 1 ) ( −1
2 − 2 )
...
k!
( −1
2 − k + 1 )
=
( ) ( ) ( ( )
1 3 5 2k − 1
(−1) k ...
2 2 2)
2
k!
∴
Since,
(2k)!
{ }} {
= (−1)k 1.3.5... (2k − 1) · 2.4.6...2k
2 k k! · 2.4.6...2k } {{ }
2 k k!
Y (s) =
∞∑
k=0
C − 1 2
k
1
s = ∑ ∞ 2k+1
k=0
= (−1)k (2k)!
2 k k!2 k k!
(−1) k (2k)!
2 2k (k!) 2 1
s 2k+1 = ∞
∑
k=0
= (−1)k (2k)!
2 2k (k!) 2
( )
(−1) k (2k)!
2 2k (k!) 2 s 2k+1
Y (s) = L {y(t)} , which is the solution of t 2 d2 y(t)
+ t dy(t) + t 2 y = 0
dt 2 dt
Denote y(t) = J 0 (t) , take the inverse Laplace Transfrom using the property
∴
J 0 (t) = L −1 { ∞
∑
k=0
}
(−1) k (2k)!
=
2 2k (k!) 2 s 2k+1
L {t n } = n!
s n+1
∞∑
k=0
{ }
(−1) k (2k)!
2 2k (k!) L =
2 s 2k+1
∞∑
k=0
(−1) k
2 2k (k!) 2 t2k
−END−