Transformation MatrixI I Rotation Matrix

Transformation Matrix I
Rotation Matrix
February 22, 2013
In a n−link robot arm, what is the position of end effector w.r.t. base reference frame ?
• By geometry inspection, but this method will become very complicated when the system is complex
• By transformation matrix, a systematic method
Review of some vector algebra
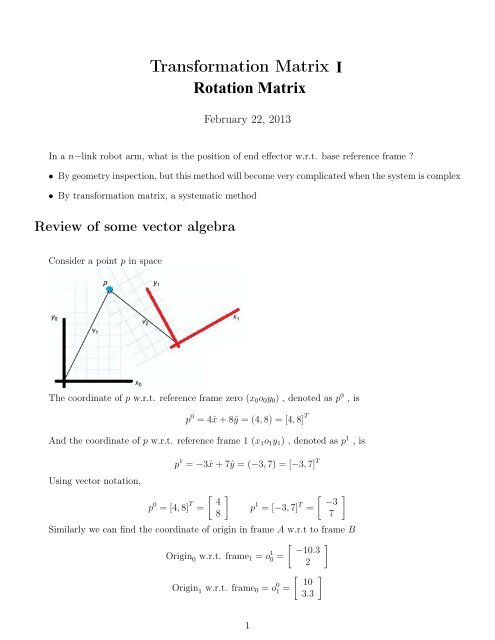
Consider a point p in space
The coordinate of p w.r.t. reference frame zero (x 0 o 0 y 0 ) , denoted as p 0 , is
p 0 = 4ˆx + 8ŷ = (4, 8) = [4, 8] T
And the coordinate of p w.r.t. reference frame 1 (x 1 o 1 y 1 ) , denoted as p 1 , is
Using vector notation,
p 1 = −3ˆx + 7ŷ = (−3, 7) = [−3, 7] T
[ ]
p 0 = [4, 8] T 4
=
8
p 1 = [−3, 7] T =
[ −3
7
Similarly we can find the coordinate of origin in frame A w.r.t to frame B
[ ] −10.3
Origin 0 w.r.t. frame 1 = o 1 0 =
2
[ ] 10
Origin 1 w.r.t. frame 0 = o 0 1 =
3.3
]
1

Transforming between Frames
How is p 0 related to p 1 ?
[ ] 4
p 0 + o 1 0 = +
8
[ ] 4
p 0 =
8
[ −10.3
2
]
=
p 1 =
[ −3
7
[ −6.3
10
]
]
≠ p 1 =
[ −3
7
Because the frame 1 are rotated, so the 2 vectors are not equal by just addition
Rotation
]
Consider 2 frame as follow
To express the unit vector (ˆx 1 , ŷ 1 ) w.r.t frame 0
That is, express x 1 and y 1 using x 0 and y 0 :
[ ] cos θ
x 0 1 =
sin θ
y 0 1 =
[ − sin θ
cos θ
Combine them into one matrix, the rotation matrix is thus
[ ]
cos θ − sin θ
R1 0 =
sin θ cos θ
Thus, a point p w.r.t frame 1 p 1 and point p w.r.t. frame 0 p 0 are related by
]
That is
p 0 = R 0 1p 1
p expressed in
frame 0
unit vector of frame 1
=
expressed in frame 0
[ cos θ − sin θ
p 0 =
sin θ cos θ
]
p 1
p expressed in
×
frame 1
2

Difference case for special θ
Since θ is the angle between 2 x axis,
When θ = 90 o R 0 1 =
[ 0 −1
1 0
That is , first swap(x, y) , then make the new x as negative.
]
When θ = 180 o R 0 1 =
[ −1 0
0 −1
]
When θ = 270 o and 360 o , or any other angle, the logic is the same.
Re-visiting the rotation matrix
Since the rotation matrix is obtained by using the x 0 1 and y1 0 as it’s column vector
⎡⎛
R1 0 = ⎣⎝ x 0 1
⎞ ⎛
⎠ ⎝ y1
0 ⎞⎤
⎠⎦
And x 0 1 , y1 0 is expressed using x 0 , y 0 , so they have 2 component
[ ] [ x-component of
x 0 x1 in frame 0
x-component of
1 =
y 0 y1 in frame 0
1 =
y component of x 1 in frame 0
y component of y 1 in frame 0
Thus
R 0 1 =
[( x-component of x1 in frame 0
y component of x 1 in frame 0
) ( x-component of y1 in frame 0
y component of y 1 in frame 0
Recall that, we can extract a vector’s component by using dot product
That is, for a vector ¯V = V xˆx + V y ŷ + V z ẑ
)]
]
Thus
R 0 1 =
V x = ¯V · ˆx
[( ) ( )]
x1 · x 0 y1 · x 0
x 1 · y 0 y 1 · y 0
And therefore, we can use same logic to find R0
1
[( ) ( )]
R0 1 x0 · x
=
1 y0 · x 1
x 0 · y 1 y 0 · y 1
These method are actually same as the graphical method, in graphical method, the diagram just
show the projection of the vector component directly in the diagram. But when the diagram is very
complicated, it is better to use the dot product method.
3

Inverse, Transpose
R 0 1 =
[ ]
x1 · x 0 y 1 · x 0
x 1 · y 0 y 1 · y 0
R 1 0 =
[ ]
x0 · x 1 y 0 · x 1
x 0 · y 1 y 0 · y 1
Since dot product is commutative, therefore, consider the transpose
Therefore
[ ]
( ) T [ ] [ ]
R
0 T x1 · x
1 =
0 y 1 · x 0 x1 · x
=
0 x 1 · y 0 x0 · x
=
1 y 0 · x 1
= R0
1 x 1 · y 0 y 1 · y 0 y 1 · x 0 y 1 · y 0 x 0 · y 1 y 0 · y 1
(
R
0
1
) T
= R
1
0
But since R 0 1 R 1 0 do the opposite thing, they are inverse to each other
Thus
(
R
0
1
) −1
= R
1
0
(
R
0
1
) −1
=
(
R
0
1
) T
Small summary
• ( R j i
) T
= R
i
j
• ( R j i
) −1
= R
i
j
• Rotation matrix is orthogonal : ( R j i
3D cases
) −1 ( )
= R
j T
i
The previous 2D case can be now treated as a 3D case
4

In 3D case, the general rotation matrix for frame i w.r.t to frame j is
⎡
⎤
x i · x j y i · x j z i · x j
R j i = ⎣ x i · y j y i · y j z i · y j
⎦
x i · z j y i · z j z i · z j
Rotation along x axis :
⎡
R1 0 (x, θ) = ⎣
1 0 0
0 cos θ − sin θ
0 sin θ cos θ
⎤
⎦
Rotation along y axis
⎡
R1 0 (y, θ) = ⎣
cos θ 0 sin θ
0 1 0
− sin θ 0 cos θ
⎤
⎦
Rotation along z axis :
⎡
R1 0 (z, θ) = ⎣
cos θ − sin θ 0
sin θ cos θ 0
0 0 1
⎤
⎦
Why rotation along y axis seems a little bit different in the sign
The rotation is defined as positive if it is rotated anti-clockwise along that axis. In the case that
rotation along the x,z axis, it fulfill this requirement. But for the case that rotate along y axis, the angle
is clockwise, so a negative sign is added into the angle.
5

Multiple Rotation
Rotation about the current frame
For point p in base frame, after the first rotation , it rotate again
Since p 2 and p 1 is related by
And p 1 and p 0 is related by
Thus
And thus for
What is p 2 w.r.t frame 0 ?
p 1 = R2p 1 2
p 0 = R1p 2 1
p 0 = R1R 0 2p 1 2
p 0 = R 0 2p 2
That is, if
R 0 2 = R 0 1R 1 2
Frame0 R0 1
−→ Frame1 R1 2
−→... Rn−1 n
−→Frame n
And
p 0 = R 0 1R 1 2...R n−2
n−1Rn
n−1 p n
R 0 n = R 0 1R 1 2...R n−2
n−1R n−1
n
−END−
6