Parabolic implosion - from discontinuity to renormalization
Parabolic implosion - from discontinuity to renormalization Parabolic implosion - from discontinuity to renormalization
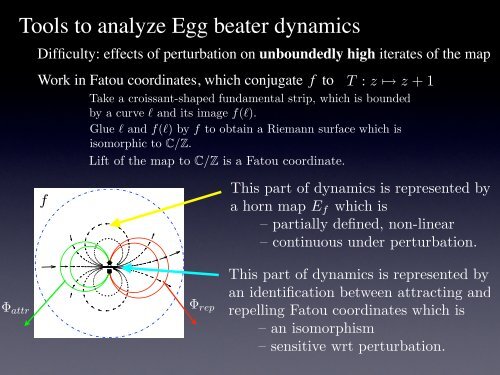
Tools to analyze Egg beater dynamics Difficulty: effects of perturbation on unboundedly high iterates of the map Work in Fatou coordinates, which conjugate f to T : z ↦→ z +1 Take a croissant-shaped fundamental strip, which is bounded by a curve l and its image f(l). Glue l and f(l) by f to obtain a Riemann surface which is isomorphic to C/Z. Lift of the map to C/Z is a Fatou coordinate. f This part of dynamics is represented by a horn map E f which is – partially defined, non-linear – continuous under perturbation. Φ∞ attr T Φ(w) rep = w C/Z + 1 CΦ attr Φ rep C/Z C This part of dynamics is represented by an identification between attracting and repelling Fatou coordinates which is – an isomorphism – sensitive wrt perturbation.
α z + . . . e 2πiα z + λ . f(z) f. = 0 . e e q z a 2 z + . . . a Fatou coordinates , i ∈ N a and Horn i ≥ N T (w) T (w) 2πi = qe = w 2πiα λ z = + 1O(z a w + 1 1 2 ) 2 ≠ 0 α ∈ C {0} small Φand Φ | arg α| map a i ∈ N attr a attr Φ< i ≥ N rep π Φ rep C/Z C/Z mod CZ C E = e 2πiα z + O(z 2 4 f0 α z + O(z 2 ) ) e 2πiα 0 (z) z + a 2 z 2 + . . . F 0 (w) = w + 1 + o(1) w = − c f 0 (z) z + holomorphic f(z) O(z f ′ (0) 2 = ) = αe near 2πiα ∈e 2πiα R0 z , + Q f (0) = 0 f ′ 0 α. (z) . . small holomorphic 0 (0) = near λ 0 f 0 (0) = 0 f 0 ′(0) = w near 0 near mod Z E λ = e 2πi ∞ p T (w) F 0 (w) w = 1w Φ1 + o(1) attr Φ w = rep C/Z − c λ ) iα = , fα 0 e(z) 2πiα small = , λz α+ asmall 2 z 2 + . . . f 0 (z) = λz + a 2 z 2 + . . . f0 w Cnear 0 near ∞ T e f q λ = mod 1 Za 2 ≠E0 0 R 0 f 0 R 0 f 2πiα , αf(z) αsmall ∈= a C e {0} small and | arg α| < π i 2πiα ∈ Nz + a i O(z ≥ N 2 ) f0 f f 0 R 0 f 0 R 0 f 0 (z) = z + O(z 2 0 (z) = e 2πi p q z + a 2 z 2 + . . . f C {0} small and | arg α| < π 0 (z) = e 2πi p q z + a 2 z 2 + . . . } small and | arg α| < π 4 ) {0} small f αf(z) ′ F 0 (0) ∈and R= e | 2πiα (w) = w + 1 2πiα arg4α| z + < f. 0 . π + o(1) w = − c near 0 near ∞ T (w) = w + 1 Φ attr Q , α small . 4 z f R 0 f 0 R 0 f 0 (z) = z + O(z 2 0 (z) = z + a 2 z 2 + mod . . . Z Ef 0 (z) = z + a 2 z 2 f0 4 E f + . . . ) R Q f Rf fRf(z) Rf = e 2πiβ z Rf(z) + O(z 2 ) λ = e f(z) = e 2πiα z + O(z 2 ) Z 2πi p q β = − 1 λ = 1 2 ≠ λ = e 2πi p q Q αa ∈ i ∈C N f {0} a i ≥small N and λ | arg 1 α| a 2 < π 0 R 0 f 0 R 0 f 0 (z) = z + O(z ≠ 2 0) α mod Z f Rf Rf(z) 4= e 2πiβ z + O(z 2 ) β = − 1 ≥ N α mod Z N f(z) a i = ≥e 2πiα N f ′ z + . . . (0) e 2πiα f(z) = e 2πiα z + . . . f Φ attr (z) , α small Φ attr (z) attr (z) + 1 f(z) + o(1) = e near 0 2πiα z w + = O(z− c Rf Rf(z) = e a i ≥ N αF ∈ 0 (w) R = Qw + 1 + o(1) 2πiβ z + O(z w = − c 2 ) β = − near 0 1 near ∞ 2 ) ) = w + 1 + o(1) w T (w) = − c α mod near Z ∞ T (w) = w + 1 near f(z) = 0 e w 2πiα near z + O(z ∞ + near 1 0Φ 2 ) T w mod Z wE (w) = w + 1 Φ attr Φ rep C/Z C Φ f0 attr (f(z)) attr near α C {0} small and | arg α| < π Φ∞ rep Φ attr T (f(z)) C/Z (w) = Cw w + attr 1(z) Φ+ attr 1 Φ rep rep (f( = f 0 w Z f ′ (0) + 1 E= + e 2πiα o(1) , α small w = − c = Φ attr (z) + 1 Φ rep (f(z)) = Φ rep (z) + 1 Φ ... (f 0 (z)) = Φ ... (z) + 1 a i ∈ N a i ≥ Nf ′ (0) = near e (z)) = Φ f0 rep (z) 2πiα , 0α small near ∞ T (w) = w + 1 Φ attr Φ rep C Φnear rep ∞C/Z T (w) C = w + 1 Φ attr w Φ rep attr (f(z)) C/Z C= Φ attr (z) 4 + Φ rep (f(z)) = Φ rep (z) + 1 E E f (z) = Φ attr attr Φ(f(z)) = Φ R −1 f0 f 0 R rep att α ∈ C {0} small and | argα α| ∈< C π R α ∈ R Q 4 1 0 f 0 R 0 f 0 (z) = z + O(z E 2 {0} small and | arg f (z) ) = Φ attr ◦ Φ −1 α| < π 0 f 0 (z) = z + E 0 f 0 R O(z 2 0 f 0 (z) = z + O(z 2 ) ) F 0 (w) = w + 1 + o(1) w = − c f0 (z) = Φ attr ◦ Φ −1 rep χ f χ f (z) = z − 1 Rf = χ f ◦ E f near40α near ∞ T (w) = w + 1 Φ w rep 0f 0 α ∈ R 0 mod Q α ∈ R Q Rf(z) = e f P ◦ ϕ E −1 1 f = P ◦ ϕ −1 f (z) = Φ attr ◦ Φ Rf β = − 1 2πiβ f 0 (z) Z= z + O(z 2 ) z + Rf f = EP O(z 2 ) Rf(z) β = = − e 12πiβ a α mod Z i ∈ NRf(z) a i ≥ N= e 2πiβ z + O(z 2 ) β = − 1 α mod Z α mod z + Z O(z 2 ) β = − 1 f0 ◦ ϕ −1 α mod Z a α mod 1 = f Z i ∈ N a i ≥ N f= ΦRf(z) f Q ◦ ϕ −1 attr Φ+ = 1e 2πiβ Φ rep z + (f(z)) O(z 2 = ) where a i ∈ N F f Q ◦ ϕ −1 0 (w) w + 1 + o(1) w = F− c Φ rep β (z) = − 1 0 Rf + α1 mod Φ(f(z)) Z attr (f(z)) 0 f= Q ◦ 0 Rϕ −1 = Φ 0 f 0 (z) = z + O(z attr (z) + 1 Φ 2 ) rep 0 (w) = near w + 01 + near o(1) ∞w = T (w) − c = Φ(z) Φ rep + (z) 1 + 1 Φ ... (f 0 (z)) = Φ ... ( 0 ∞ (−∞, = w near + 0 1Φnear attr ∞Φ rep T (w) C/Z = = Φ a 1 ± 0 ∞ f (−∞, 1 −1] P ◦ ϕ −1 w + C1 Φ attr r(f(z)) = rep Φ(z) 1 Φ(f(z)) w −1] Φ(z) 1 mod Z attr (z) + 1 Φ rep (f(z)) = Φ rep (z) + w1 Φ(f(z)) = Φ(z) + 1 f0 mod Z E f0 rep(z) (z)) ttr ◦ + Φ= 1 −1 rep Φ attr fE f0 (z) (z) Rf + = 1 ΦRf(z) attr Φ rep ◦(f(z)) Φ= −1 e 2πiβ rep = z Φ+ rep O(z (z) 2 + ) 1 β = Φ a ... − 1 (f 2 ± α 0 (z)) mod = Z Φ ... (z) + 1 C R Z Q D H R Q C/Z C ∗ D ∗ C C D (−∞, −1]
- Page 1 and 2: Parabolic implosion from discontinu
- Page 3 and 4: Basic definitions f polynomial (or
- Page 5 and 6: Egg beater or Douady-Hubbard’s ge
- Page 7: Pick a point w in the box on the ri
- Page 11 and 12: morphic near 0 f 0 (0) = 0 f ′ 0
- Page 13 and 14: Further results Discontinuity of st
- Page 15 and 16: Near-parabolic Renormalization (cyl
- Page 17 and 18: Applications (work in progress) The
Tools <strong>to</strong> analyze Egg beater dynamics<br />
Difficulty: effects of perturbation on unboundedly high iterates of the map<br />
Work in Fa<strong>to</strong>u coordinates, which conjugate f <strong>to</strong> T : z ↦→ z +1<br />
Take a croissant-shaped fundamental strip, which is bounded<br />
by a curve l and its image f(l).<br />
Glue l and f(l) by f <strong>to</strong> obtain a Riemann surface which is<br />
isomorphic <strong>to</strong> C/Z.<br />
Lift of the map <strong>to</strong> C/Z is a Fa<strong>to</strong>u coordinate.<br />
f<br />
This part of dynamics is represented by<br />
a horn map E f which is<br />
– partially defined, non-linear<br />
– continuous under perturbation.<br />
Φ∞ attr<br />
T Φ(w) rep<br />
= w C/Z + 1 CΦ attr Φ rep C/Z C<br />
This part of dynamics is represented by<br />
an identification between attracting and<br />
repelling Fa<strong>to</strong>u coordinates which is<br />
– an isomorphism<br />
– sensitive wrt perturbation.