Ch 5 Worksheet Key

Ch 5 Worksheet L1 Key
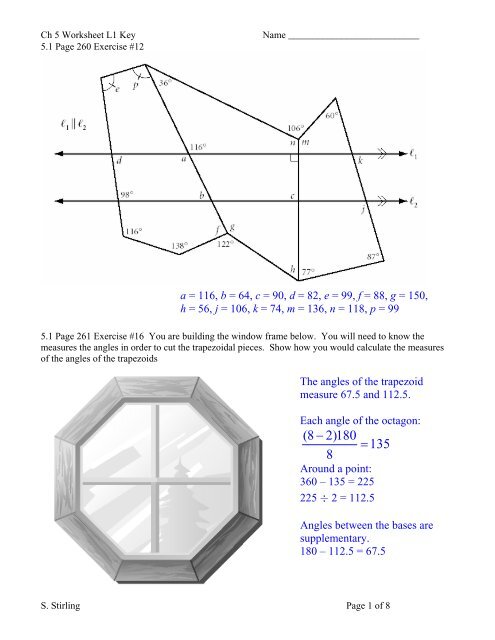
5.1 Page 260 Exercise #12
Name ___________________________
a = 116, b = 64, c = 90, d = 82, e = 99, f = 88, g = 150,
h = 56, j = 106, k = 74, m = 136, n = 118, p = 99
5.1 Page 261 Exercise #16 You are building the window frame below. You will need to know the
measures the angles in order to cut the trapezoidal pieces. Show how you would calculate the measures
of the angles of the trapezoids
The angles of the trapezoid
measure 67.5 and 112.5.
Each angle of the octagon:
(8 − 2)180
= 135
8
Around a point:
360 – 135 = 225
225 ÷ 2 = 112.5
Angles between the bases are
supplementary.
180 – 112.5 = 67.5
S. Stirling Page 1 of 8

Ch 5 Worksheet L1 Key
Name ___________________________
Proof of the Kite Angles Conjecture
Conjecture: The nonvertex angles of a kite are congruent.
K
Given: Kite KITE with diagonal KT .
Prove: The nonvertex angles are congruent, ∠E ≅∠ I .
E
I
Kite KITE
KT
=
KT
T
Given
KE KI
ET = IT
Def. of Kite
= and
Same Segment.
ΔKET
≅ ΔKT
I
SSS Cong. Conj.
∠E
≅∠I
CPCTC or
Def. cong.
triangles
5.3 Page 272 Exercise #9 Proof of Kite Angle Bisector Conjecture
The vertex angles of a kite are bisected by a diagonal.
BN
≅
BN
Same Segment.
BE ≅ BY
YN ≅ EN
Given or
Def. of Kite
ΔBYN
≅ Δ BEN
SSS Cong. Conj.
BN bisects
BN bisects
∠1≅∠
2
∠3≅∠
4
∠ YBE
Def. angle bisector
CPCTC or Def.
cong. triangles
∠ YNE
S. Stirling Page 2 of 8

Ch 5 Worksheet L1 Key
Proof of the Kite Diagonals Conjecture
Conjecture: The diagonals of a kite are perpendicular.
Given: Kite ABCD with diagonals DB and AC .
Prove: The diagonals are perpendicular. DB ⊥ AC .
Kite ABCD
∠DAI
≅∠BAI
Name ___________________________
C
D
I
B
A
Given
AD = AB
Def. of Kite
AI = AI
Same Segment.
Diag. bisect vertex angles.
ΔDAI
≅ ΔBAI
SAS Cong. Conj.
DB ⊥ AC
Def. of Perpendicular
∠DIA
≅∠ BIA
CPCTC
m∠ DIA+ m∠ BIA=
180
Linear Pair Conj.
m∠ DIA= m∠ BIA= 90°
Algebra
Proof of the Kite Diagonal Bisector Conjecture
Conjecture: The diagonal connecting the vertex angles of a kite
is the perpendicular bisector of the other diagonal.
Given: Kite ABCD with diagonals DB and AC .
D
I
A
Prove: AC is the perpendicular bisector of DB .
B
Kite ABCD
Given
∠DAI
≅∠BAI
Diag. bisect vertex angles.
C
DB
⊥
AC
AD = AB
Def. of Kite
AI = AI
Same Segment.
ΔDAI
≅ ΔBAI
SAS Cong. Conj.
DI
CPCTC
= IB
Diag. of kite are
Perpendicular
AC is the perpendicular bisector of DB
Def. of perp. bisector.
S. Stirling Page 3 of 8

Ch 5 Worksheet L1 Key
Name ___________________________
5.3 Page 271 Proof of Isosceles Trapezoid Diagonals Conjecture
Conjecture: The diagonals of an isosceles trapezoid are congruent.
Given: Isosceles trapezoid TRAP with TP = RA.
Show: Diagonals are congruent, TA = RP.
TR
= TR
PT
Given
= RA
Same Segment.
Isosceles trapezoid TRAP
Given
m∠ PTR= m∠TRA
Isosceles Trap. base angles =
ΔPTR
≅ ΔART
SAS Cong. Conj.
TA = RP
CPCTC
5.3 Page 274 Exercise #19
5.4 Page 279 Exercise #14
a = 80, b = 20, c = 160, d = 20, e = 80, f = 80,
g = 110, h = 70, m = 110, n = 100
a = 54, b = 72, c = 108, d = 72, e = 162, f = 18, g = 81,
h = 49.5, i = 130.5, k = 49.5, m = 162, n = 99
S. Stirling Page 4 of 8

Ch 5 Worksheet L1 Key
Name ___________________________
Proof of the Parallelogram Opposite Angles Conjecture
Conjecture: The opposite angles of a parallelogram are congruent.
R
2
Given: Parallelogram PARL with diagonal AL .
Prove: ∠PAR ≅∠PLR
and ∠R≅∠ P.
1
L
Parallelogram
PARL
Given
LP
AR
Def. of Parallelogram
PA
LR
Def. of Parallelogram
m∠ 1=
m∠
4
If ||, AIA cong.
m∠ R= m∠
P
m∠ 2=
m∠
3
If ||, AIA cong.
m∠ 2+ m∠ 1= m∠ 3+ m∠
4
A
Addition
m∠ PLR= m∠
PAR
4
3
P
If 2 angles of one triangle =
2 angles of another, the 3 rd
angles are =.
Substitution
Proof of the Parallelogram Opposite Sides Conjecture
Conjecture: The opposite sides of a parallelogram are congruent.
P
A
Given: Parallelogram PARL with diagonal PR .
Prove: PL ≅ RA and PA ≅ LR .
Parallelogram
PARL
Given
PA
LR
Def. of Parallelogram
∠APR
≅∠LRP
If ||, AIA cong.
L
R
∠L
≅∠ A
Opposite angles of
Parallelogram =
ΔPAR
≅ΔRLP
AAS Cong. Conj.
PR
=
PR
PL
≅ RA and PA ≅ LR
Same Segment.
CPCTC
S. Stirling Page 5 of 8

Ch 5 Worksheet L1 Key
Name ___________________________
5.5 Page 284 Exercise #13 Proof of the Parallelogram Diagonals Conj.
The diagonals of a parallelogram bisect each other.
given
∠EAL
≅ ∠ALN
ΔETA
≅ΔNTL
def parallelogram
EA
≅ LN
LT ≅ TA
EN &
LA bisect eachother.
5.6 Proofs
Proof of the Rhombus Diagonals Angles Conjecture
Conjecture: The diagonals of a rhombus bisect the angles of the rhombus.
Given: Rhombus RHOM with diagonal HM .
Prove: HM bisects ∠RHO
and ∠ RMO .
Rhombus RHOM
Given
RH = HO = OM = MR
Def. of Rhombus
HM
HM bisects
∠ RMO
= HM
Same Segment.
∠RHO
Def. of angle bisector
and
R
H
O
M
ΔMRH
≅Δ MOH
SSS Cong. Conj.
∠RHM
≅∠ OHM
∠RMH
≅∠OMH
CPCTC
S. Stirling Page 6 of 8

Ch 5 Worksheet L1 Key
Name ___________________________
Proof of the Rhombus Diagonals Conjecture
H
Conjecture: The diagonals of a rhombus are perpendicular, and R
they bisect each other.
X
Given: Rhombus RHOM with diagonals HM and RO .
Prove: HM and RO are perpendicular bisectors of each other.
M
O
Rhombus RHOM
Given
RH = RM
Def of Rhombus
RX = RX
Same Segment
HX
RX
ΔRXH
= XM
= XO
Diagonals of a parallelogram
bisect each other.
≅ ΔRXM
SSS Cong. Conj.
m∠ RXH + m∠ RXM = 180
Linear Pair
HM and RO are
perpendicular bisectors of
each other.
Def of Perp. Bisector
RO ⊥ HM
Def of Perp.
m∠ RXH = m∠ RXM = 90°
CPCTC and Algebra
5.6 Page 297 Exercise #28
a = 54, b = 36, c = 72, d = 108, e = 36, f = 144, g = 18,
h = 48, i = 48, k = 84
S. Stirling Page 7 of 8

Ch 5 Worksheet L1 Key
5.R Page 305 Exercise #13
Name ___________________________
Kite
Isosceles
trapezoid
Parallelogram Rhombus Rectangle Square
Opposite sides are No One pair Yes Yes Yes Yes
parallel
Opposite sides are No One pair Yes Yes Yes Yes
congruent
Opposite angles are Non-Vertex No Yes Yes Yes Yes
congruent
Diagonals bisect each No No Yes Yes Yes Yes
other
Diagonals are Yes No No Yes No Yes
perpendicular
Diagonals are No Yes No No Yes Yes
congruent
Exactly one line of Yes Yes No No No No
symmetry
Exactly two lines of
symmetry
No No No Yes Yes Yes 4
5.R Page 305 Exercise #15
a = 120, b = 60, c = 60, d = 120, e = 60, f = 30, g = 108,
m = 24, p = 84
S. Stirling Page 8 of 8