Itinerant Spin Dynamics in Structures of ... - Jacobs University
Itinerant Spin Dynamics in Structures of ... - Jacobs University Itinerant Spin Dynamics in Structures of ... - Jacobs University
86 Chapter 5: Spin Hall Effect • localized site orbitals are of s symmetry. Applying this assumptions the tight-binding version of the Hamiltonian is given by H = H 0 +H R +H D,lin +H D,cubic , (5.7) = ∑ ǫ i c † i,σ c i,σ −t ∑ c † i,σ c j,σ i,σ 〈i,j〉,σ ∑ {c † l,m,σ (iσ ′ y ) σσ ′c l+1,m,σ −c † l,m,σ (iσ ′ x ) σσ ′c l,m+1,σ } + α 2 2a + α 1 2a σ,σ ′ l,m ∑ {c † l,m,σ (iσ ′ x ) σσ ′c l+1,m,σ −c † l,m,σ (iσ ′ y ) σσ ′c l,m+1,σ } σ,σ ′ l,m ⎧ ⎪⎨ + γ ∑ D a 3 {c † ⎪ l,m,σ (−iσ ⎩ ′ x ) σσ ′c l+1,m,σ +c † l,m,σ (iσ ′ y ) σσ ′c l,m+1,σ } σ,σ ′ l,m σ,σ ′ l,m ⎫ + 1 ∑ ⎪⎬ {c † 2 l,m,σ (i(σ ′ x −σ y )) σσ ′c l+1,m+1,σ +c † l,m,σ (i(σ ′ x +σ y )) σσ ′c l+1,m−1,σ } ⎪⎭ +h.c.. (5.8) where c † i,σ is the creation operator at site index i with spin σ =↑,↓ and c† l,m,σ the creation operator at site (index x ,index y ) = (l,m). The hopping coupling t is given by t = 1/(2m e a) with the lattice constant a. In the following we take the cubic Dresselhaus term only as a shift of, ˜α 1 = α 1 − 2γ D /a 2 , according to Eq.(3.44), and assume a clean system, i.e the on-site energy is set to ǫ i = 0. Applying a Fourier transformation to Eq.(5.7) and going to momentum space we get (we set a ≡ 1) ⎧ H = ∑ ⎪⎨ −2t(cos(k ⎪ x )+cos(k y )) δ σσ ′c † kx,ky ⎩ } {{ } k,σ c ′ k,σ σ,σ ′ E 0 + (α 2 sin(k y )− ˜α 1 sin(k x ))c † k,σ ′ (σ x ) σσ ′c k,σ + (˜α 1 sin(k y )−α 2 sin(k x ))c † k,σ ′ (σ y ) σσ ′c k,σ } . (5.9) The corresponding eigenvalues are E ± (k) = E 0 (k)±∆(k) (5.10)
Chapter 5: Spin Hall Effect 87 with ∆(k) = √ (α 2 2 + ˜α2 1 )(sin(k x) 2 +sin(k y ) 2 )−4α 2˜α 1 sin(k x )sin(k y ) (E − (k) is plotted in Fig.5.1). The eigenvectors are given by ⎛ |+/−〉 = √ 1 ⎝ 2 ∓({˜α 1 sin(k x)−α 2 sin(k y)}+i{˜α 1 sin(k y)−α 2 sin(k x)}) ∆ 1 ⎞ ⎠ (5.11) (a) (b) Figure 5.1: Energy band E − (k), Eq.(5.10) is plotted for pure Rashba SOC as function of wave vector k. The contour lines indicate the energy at which one finds a Van Hove singularity in the DOS (below half-filling). To calculate the SHE using Kubo formula, Eq.(5.5), we have to calculate the matrix elements of spin current operator and velocity operator. In the site basis of our lattice they have the following form: 〈n|v|m〉 = 〈0| ∑ ij αβ = 〈0| ∑ ij αβ ψn(i,α)c ∗ iα vψ m (j,β)c † jβ |0〉, (5.12) ψn(i,α)c ∗ 1 iα i [r,H]ψ m(j,β)c † jβ |0〉, (5.13) with r = ∑ kσ r kc † kσ c kσ = 1 i 〈0|∑ kγ ∑ ψn ∗ (i,α)c iα[r k c † kγ c kγ]Hc † jβ ψ m(j,β) ij αβ −ψ ∗ n(i,α)c iα 1 i H[c† kγ c kγr k ]c † jβ ψ m(j,β)|0〉, (5.14)
- Page 45 and 46: Chapter 3: WL/WAL Crossover and Spi
- Page 47 and 48: Chapter 3: WL/WAL Crossover and Spi
- Page 49 and 50: Chapter 3: WL/WAL Crossover and Spi
- Page 51 and 52: Chapter 3: WL/WAL Crossover and Spi
- Page 53 and 54: Chapter 3: WL/WAL Crossover and Spi
- Page 55 and 56: Chapter 3: WL/WAL Crossover and Spi
- Page 57 and 58: Chapter 3: WL/WAL Crossover and Spi
- Page 59 and 60: Chapter 3: WL/WAL Crossover and Spi
- Page 61 and 62: Chapter 3: WL/WAL Crossover and Spi
- Page 63 and 64: Chapter 3: WL/WAL Crossover and Spi
- Page 65 and 66: Chapter 3: WL/WAL Crossover and Spi
- Page 67 and 68: Chapter 3: WL/WAL Crossover and Spi
- Page 69 and 70: Chapter 3: WL/WAL Crossover and Spi
- Page 71 and 72: Chapter 3: WL/WAL Crossover and Spi
- Page 73 and 74: Chapter 3: WL/WAL Crossover and Spi
- Page 75 and 76: Chapter 3: WL/WAL Crossover and Spi
- Page 77 and 78: Chapter 4 Direction Dependence of S
- Page 79 and 80: Chapter 4: Direction Dependence of
- Page 81 and 82: Chapter 4: Direction Dependence of
- Page 83 and 84: Chapter 4: Direction Dependence of
- Page 85 and 86: Chapter 4: Direction Dependence of
- Page 87 and 88: Chapter 4: Direction Dependence of
- Page 89 and 90: Chapter 4: Direction Dependence of
- Page 91 and 92: Chapter 4: Direction Dependence of
- Page 93 and 94: Chapter 5 Spin Hall Effect 5.1 Intr
- Page 95: Chapter 5: Spin Hall Effect 85 curr
- Page 99 and 100: Chapter 5: Spin Hall Effect 89 1.0
- Page 101 and 102: Chapter 5: Spin Hall Effect 91 as s
- Page 103 and 104: Chapter 5: Spin Hall Effect 93 V⩵
- Page 105 and 106: Chapter 5: Spin Hall Effect 95 0.4
- Page 107 and 108: Chapter 5: Spin Hall Effect 97 oper
- Page 109 and 110: Chapter 5: Spin Hall Effect 99 the
- Page 111 and 112: Chapter 5: Spin Hall Effect 101 str
- Page 113 and 114: Chapter 5: Spin Hall Effect 103 Com
- Page 115 and 116: Chapter 5: Spin Hall Effect 105 Fin
- Page 117 and 118: Chapter 6: Critical Discussion and
- Page 119 and 120: Chapter 6: Critical Discussion and
- Page 121 and 122: List of Figures 111 3.3 Exemplifica
- Page 123 and 124: List of Figures 113 4.2 The spin de
- Page 125 and 126: List of Tables 3.1 Singlet and trip
- Page 127 and 128: Bibliography 117 [BB04] [BBF + 88]
- Page 129 and 130: Bibliography 119 [DP71b] [DP71c] [D
- Page 131 and 132: Bibliography 121 [HSM + 06] [HSM +
- Page 133 and 134: Bibliography 123 [MACR06] T. Mickli
- Page 135 and 136: Bibliography 125 [PMT88] [PP95] [PT
- Page 137 and 138: Bibliography 127 [Tor56] H. C. Torr
- Page 139 and 140: Appendix A SOC Strength in the Expe
- Page 141 and 142: Appendix A: SOC Strength in the Exp
- Page 143 and 144: Appendix B: Linear Response 133 in
- Page 145 and 146: Appendix B: Linear Response 135 Pro
Chapter 5: <strong>Sp<strong>in</strong></strong> Hall Effect 87<br />
with ∆(k) = √ (α 2 2 + ˜α2 1 )(s<strong>in</strong>(k x) 2 +s<strong>in</strong>(k y ) 2 )−4α 2˜α 1 s<strong>in</strong>(k x )s<strong>in</strong>(k y )<br />
(E − (k) is plotted <strong>in</strong> Fig.5.1). The eigenvectors are given by<br />
⎛<br />
|+/−〉 = √ 1 ⎝<br />
2<br />
∓({˜α 1 s<strong>in</strong>(k x)−α 2 s<strong>in</strong>(k y)}+i{˜α 1 s<strong>in</strong>(k y)−α 2 s<strong>in</strong>(k x)})<br />
∆<br />
1<br />
⎞<br />
⎠ (5.11)<br />
(a)<br />
(b)<br />
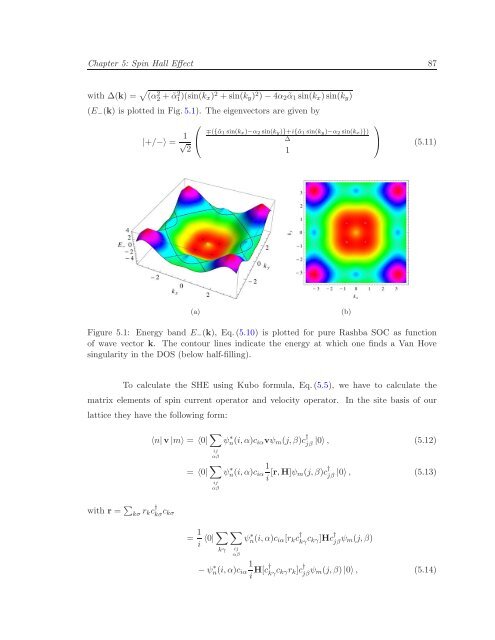
Figure 5.1: Energy band E − (k), Eq.(5.10) is plotted for pure Rashba SOC as function<br />
<strong>of</strong> wave vector k. The contour l<strong>in</strong>es <strong>in</strong>dicate the energy at which one f<strong>in</strong>ds a Van Hove<br />
s<strong>in</strong>gularity <strong>in</strong> the DOS (below half-fill<strong>in</strong>g).<br />
To calculate the SHE us<strong>in</strong>g Kubo formula, Eq.(5.5), we have to calculate the<br />
matrix elements <strong>of</strong> sp<strong>in</strong> current operator and velocity operator. In the site basis <strong>of</strong> our<br />
lattice they have the follow<strong>in</strong>g form:<br />
〈n|v|m〉 = 〈0| ∑ ij<br />
αβ<br />
= 〈0| ∑ ij<br />
αβ<br />
ψn(i,α)c ∗ iα vψ m (j,β)c † jβ<br />
|0〉, (5.12)<br />
ψn(i,α)c ∗ 1<br />
iα<br />
i [r,H]ψ m(j,β)c † jβ<br />
|0〉, (5.13)<br />
with r = ∑ kσ r kc † kσ c kσ<br />
= 1 i 〈0|∑ kγ<br />
∑<br />
ψn ∗ (i,α)c iα[r k c † kγ c kγ]Hc † jβ ψ m(j,β)<br />
ij<br />
αβ<br />
−ψ ∗ n(i,α)c iα<br />
1<br />
i H[c† kγ c kγr k ]c † jβ ψ m(j,β)|0〉, (5.14)