Itinerant Spin Dynamics in Structures of ... - Jacobs University
Itinerant Spin Dynamics in Structures of ... - Jacobs University
Itinerant Spin Dynamics in Structures of ... - Jacobs University
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Chapter 4: Direction Dependence <strong>of</strong> <strong>Sp<strong>in</strong></strong> Relaxation and Diffusive-Ballistic Crossover 73<br />
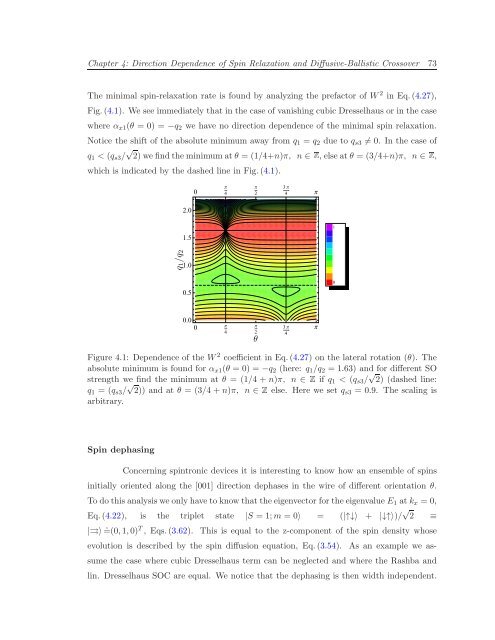
The m<strong>in</strong>imal sp<strong>in</strong>-relaxation rate is found by analyz<strong>in</strong>g the prefactor <strong>of</strong> W 2 <strong>in</strong> Eq.(4.27),<br />
Fig.(4.1). We see immediately that <strong>in</strong> the case <strong>of</strong> vanish<strong>in</strong>g cubic Dresselhaus or <strong>in</strong> the case<br />
where α x1 (θ = 0) = −q 2 we have no direction dependence <strong>of</strong> the m<strong>in</strong>imal sp<strong>in</strong> relaxation.<br />
Notice the shift <strong>of</strong> the absolute m<strong>in</strong>imum away from q 1 = q 2 due to q s3 ≠ 0. In the case <strong>of</strong><br />
q 1 < (q s3 / √ 2)wef<strong>in</strong>dthem<strong>in</strong>imumatθ = (1/4+n)π, n ∈, elseatθ = (3/4+n)π, n ∈,<br />
which is <strong>in</strong>dicated by the dashed l<strong>in</strong>e <strong>in</strong> Fig.(4.1).<br />
Π<br />
0 <br />
4<br />
Π<br />
<br />
2<br />
3Π<br />
<br />
4 Π<br />
2.0<br />
1.5<br />
1<br />
q1/q2<br />
1.0<br />
0.5<br />
0<br />
0.0<br />
Π<br />
0 <br />
4<br />
Π<br />
<br />
3Π<br />
2 <br />
θ<br />
4<br />
Π<br />
Figure 4.1: Dependence <strong>of</strong> the W 2 coefficient <strong>in</strong> Eq.(4.27) on the lateral rotation (θ). The<br />
absolute m<strong>in</strong>imum is found for α x1 (θ = 0) = −q 2 (here: q 1 /q 2 = 1.63) and for different SO<br />
strength we f<strong>in</strong>d the m<strong>in</strong>imum at θ = (1/4 + n)π, n ∈if q 1 < (q s3 / √ 2) (dashed l<strong>in</strong>e:<br />
q 1 = (q s3 / √ 2)) and at θ = (3/4 +n)π, n ∈else. Here we set q s3 = 0.9. The scal<strong>in</strong>g is<br />
arbitrary.<br />
<strong>Sp<strong>in</strong></strong> dephas<strong>in</strong>g<br />
Concern<strong>in</strong>g sp<strong>in</strong>tronic devices it is <strong>in</strong>terest<strong>in</strong>g to know how an ensemble <strong>of</strong> sp<strong>in</strong>s<br />
<strong>in</strong>itially oriented along the [001] direction dephases <strong>in</strong> the wire <strong>of</strong> different orientation θ.<br />
Todothisanalysisweonlyhavetoknowthattheeigenvector fortheeigenvalueE 1 atk x = 0,<br />
Eq.(4.22), is the triplet state |S = 1;m = 0〉 = (|↑↓〉 + |↓↑〉)/ √ 2 ≡<br />
|⇉〉 ˆ=(0,1,0) T , Eqs.(3.62). This is equal to the z-component <strong>of</strong> the sp<strong>in</strong> density whose<br />
evolution is described by the sp<strong>in</strong> diffusion equation, Eq.(3.54). As an example we assume<br />
the case where cubic Dresselhaus term can be neglected and where the Rashba and<br />
l<strong>in</strong>. Dresselhaus SOC are equal. We notice that the dephas<strong>in</strong>g is then width <strong>in</strong>dependent.