Solution 8 (Dynamic Programming) Exercise 1 ... - ETH Zürich

Exercises
Informatik II for D-MAVT
Sommersemester 2007
Solution 8
(Dynamic Programming)
Institute for Computational Science
Dept. of Computer Science, ETH Zürich
Prof. Dr. Joachim M. Buhmann,
Prof. Dr. Ivo Sbalzarini, Dr. Bernd Fischer
Tel. +41-1-632 6527
E-Mail {jbuhmann,ivos,bernd.fischer}@inf.ethz.ch
Web http://people.inf.ethz.ch/befische/info2
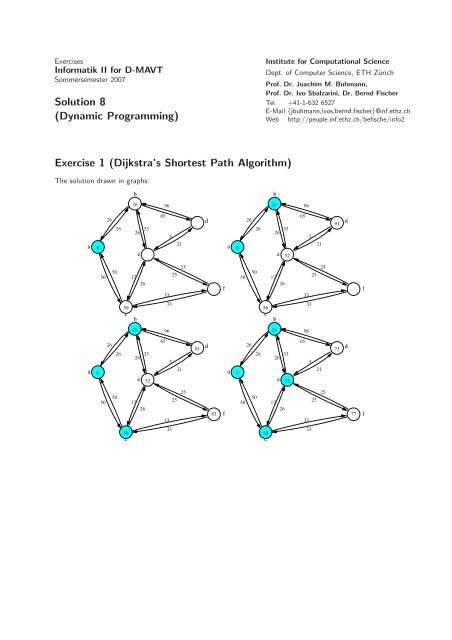
Exercise 1 (Dijkstra’s Shortest Path Algorithm)
The solution drawn in graphs:
b
b
26
96
26
96
a
0
26
26
26
33
e
65
5
21
d
a
0
26
26
26
33
e 52
65
5
21
91
d
50
50
17
26
25
33
25
f
50
50
17
26
25
33
25
f
50
c
b
33
50
c
b
33
26
96
26
96
a
0
26
26
26
33
e 52
65
5
21
91
d
a
0
26
26
26
33
e 52
65
5
21
73
d
50
50
17
26
33
25
25
83
f
50
50
17
26
33
25
25
77
f
50
c
33
50
c
33

b
26
96
26
96
a
0
26
26
26
33
e 52
65
5
21
73
d
a
0
26
26
26
33
e 52
65
5
21
73
d
50
50
17
26
33
25
25
77
f
50
50
17
26
33
25
25
77
f
50
c
33
50
c
33
The solution in a table:
node a b c d e f
S X
costs 0 26 50
bp - a a
S X X
costs 0 26 50 91 52
bp - a a b b
S X X X
costs 0 26 50 91 52 83
bp - a a b b c
S X X X X
costs 0 26 50 73 52 77
bp - a a e b e
S X X X X X
costs 0 26 50 73 52 77
bp - a a e b e
S X X X X X X
costs 0 26 50 73 52 77
bp - a a e b e
The following drawing shows the trace back path for the shortest path of node f.
node
a
b c d e
f
bp
−
a a e b
e
The shortest path is thus
a → b → e → f
Exercise 2 (Dynamic Programing and Recursive Functions)
1. A recursive definition of the shortest path problem would be as follows: Given a graph G with vertices
V = 1,...,n and edges E ⊂ V × V with weights w ij , the shortest path S(s,t) from s to t is defined
by the recursive function R(s,t,A) as
S(s,t) = R (s,t,V \ {t}) (1)
R(s,t,A) = min
i∈S {R(s,i,A \ {t}) + w it} (2)
2

2. To compute the runtime, we define a helper function c(n), that is the cost for the computation of the
shortest path in a graph with n nodes. c(n) is defined recursively as well.
c(n) = O ((n − 1) · c(n − 1)) (3)
The set S has a size of at most n − 1. For every element in S we have to solve one shortest path
problem on a graph with n − 1 nodes.
Thus the runtime of the algorithm is O((n − 1)!).
Exercise 3 (List Scheduling)
0001 function a=listscheduling(t,m)
0002
0003 % The number of jobs is n
0004 n = size(t,2);
0005
0006 % The vector machineload stores the load of the machines. In the
0007 % beginning all machines are idle.
0008 machineload(1:m) = 0.0;
0009
0010 % Assign the jobs to the machines in the order they are written in the
0011 % input vector
0012 for i=1:n
0013
0014 % Find the machine that is minimal loaded up to now
0015 [M,I] = min(machineload);
0016
0017 % I(1) now contains the index of the machine that is minimal loaded
0018 a(i) = I(1);
0019
0020 % Update the machine load.
0021 machineload(I(1)) = machineload(I(1)) + t(i);
0022 end;
0023
3