N-Body Simulation

N-Body Simulation
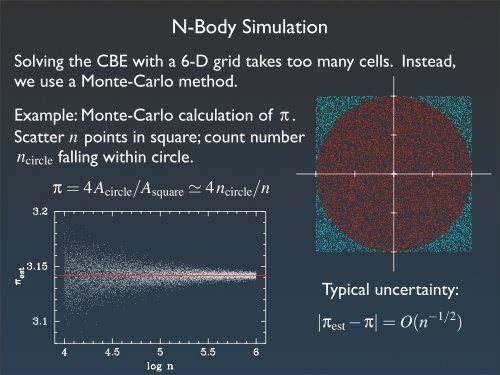
Solving the CBE with a 6-D grid takes too many cells. Instead,
we use a Monte-Carlo method.
Example: Monte-Carlo calculation of π .
Scatter
n circle
n
points in square; count number
falling within circle.
π = 4A circle /A square ≃ 4n circle /n
Typical uncertainty:
|π est − π| = O(n −1/2 )

Representing the Distribution Function
Replace smooth distribution with bodies:
f (⃗r,⃗v) → {(m i ,⃗r i ,⃗v i ) | i = 1,...,N}
f (⃗r,⃗v) ≃
This requires that for any phase-space volume V,
Z
〈 〉
d⃗rd⃗v f (⃗r,⃗v) = ∑ m (⃗ri ,⃗v i )∈V i
E.g., select (⃗r i ,⃗v i ) with probability proportional to f (⃗r i ,⃗v i ), and
assign all bodies equal mass:
V
N
∑ m i δ 3 (⃗r −⃗r i )δ 3 (⃗v −⃗v i )
i=1
m i = 1 N
Z
d⃗rd⃗v f (⃗r,⃗v)

Advancing Time
Move bodies along phase flow (method of characteristics):
Estimate potential from N-body representation:
This will yield the usual N-body equation for point masses. But
singular potentials are awkward, so we smooth the density field:
δ 3 (⃗r −⃗r i ) → 3
4π
ε 2
(|⃗r −⃗r i | 2 + ε 2 ) 5/2
This substitution yields the following equations of motion:
d⃗r i
dt =⃗v i
(˙ ⃗r i , ˙ ⃗v i ) = (⃗v i ,−(∇Φ) i )
∇ 2 Φ ∣ ∣
⃗r
= 4πG
d⃗v i
dt = N
∑
j≠i
N
∑ m i δ 3 (⃗r −⃗r i )
i=1
Gm j (⃗r j −⃗r i )
(|⃗r j −⃗r i | 2 + ε 2 ) 3/2
Plummer (1911)
smoothing
Aarseth (1963)

Comments
1. N-body models relax at roughly the same rate as real stellar
systems with the same
N
; the relaxation time is
t r ≃
N
8ln(R /ε) t c
2. Sampling proportional to f (⃗r i ,⃗v i ) is the simplest option, but
not the only one; other weighting schemes are also possible.
E.g., use different masses when sampling f s (⃗r,⃗v) and f d (⃗r,⃗v) , or
make m i depend on f (⃗r i ,⃗v i ) . But note effect on relaxation time!
3. Plummer smoothing is just one of many possibilities, and may
not be optimal; one alternative with less of a “tail” is
δ 3 (⃗r −⃗r i ) → 15
ε 4
8π (|⃗r −⃗r i | 2 + ε 2 ) 7/2 Dehnen (2001)

Force Calculation: Direct Summation
Simplest method: sum over all other bodies.
⃗a i =
N
∑
j≠i
Gm j (⃗r j −⃗r i )
(|⃗r j −⃗r i | 2 + ε 2 ) 3/2
Advantages: robust, accurate, completely general.
Disadvantage: computational cost per body is O(N) ;
need O(N 2 ) operations to compute forces on all bodies.
However, direct summation is a good fit with
1. Individual timesteps (see Sverre’s lectures)
2. Specialized hardware (see Simon’s lectures)

Tree Codes
Long-range gravitational field dominated
by monopole term:
φ ≃ − Gm
r + O(r−3 )
Divide system into hierarchy (i.e.“tree”)
of compact cells:
Saul Steinberg, “A view of the World from 9 th Avenue, 1976.
Barnes & Hut (1986)
Replace sum over N bodies with sum
over N c ≃ O(logN) cells; cost to find
forces on all bodies is O(N logN) .
N
∑
i
→
N c
∑
c

Tree Codes Continued
1. To compute potential at ⃗r due to a cell c :
a) if c is “too close” to ⃗r , sum the potentials of its sub-cells;
b) otherwise, approximate the potential as −Gm c /|⃗r −⃗r c | .
2. “too close” can be defined in various ways; e.g.:
cell’s center
of mass
a) geometrically: |⃗r −⃗r c | < l c /θ (BH86) or < l c /θ + δ c (B95),
b) dynamically: |⃗r −⃗r c | 4 < GM c l 2 c/α|⃗a| (GADGET-2: Springel 2005).
3. Different tree structures give roughly equivalent results:
a) oct-trees: 1 cube → 8 cubes (Barnes & Hut 1986),
b) kd trees: divide at median along x,y,z (Dikaiakos & Stadel 1996),
c) particle trees: group nearest neighbors (Appel 1985, Press 1986).
4. Higher moments improve accuracy:
a) quadrupole potential term:
1
2Gδ⃗r · Q c · δ⃗r /δr 5 (Hernquist 1987),
b) source/sink symmet. momentum cons., O(N) (Dehnen 2000).

Self-Consistent Field Method
Represent potential and density as sums:
Φ(⃗r) = ∑
k
A k Φ k (⃗r),
ρ(⃗r) = ∑
k
A k ρ k (⃗r)
where are coefficients and the basis functions and are
A k
bi-orthogonal and satisfy the PE:
I k δ k k
′ =
Z
d⃗r ρ k (⃗r)[Φ k ′(⃗r)] ∗ ,
The coefficients are computed using overlap integrals:
A k = 1 Z
d⃗r ρ(⃗r)[Φ k (⃗r)] ∗ = 1 ∑m i [Φ k (⃗r i )] ∗
I k I k
Φ k
∇ 2 Φ k = 4πGρ k
The cost of calculating forces on all bodies is just O(N) .
ρ k
With the right basis set, SCFM yields good forces for spheroidal
systems with only a few terms (Hernquist & Ostriker 1992).

Time Step Algorithms
The underlying symmetry of the N-body equation of motion
becomes evident in Hamiltonian formulation:
d⃗r
dt = ∂H
∂⃗p ,
d⃗p
dt = −∂H ∂⃗r
This symmetry has important consequences:
1. dynamical evolution conserves phase space volume
2. Hamiltonian systems have no attractors
3. dynamical evolution is reversible.
Hamiltonian systems are not structurally stable; most
integrators will not preserve these properties.
An integration algorithm with Hamiltonian symmetry is
desirable; such an integrator is known as symplectic.

Leapfrog Integrator
This very simple integrator explicitly preserves the symmetry
of the Hamiltonian equations of motion:
⃗r [k+1]
i
⃗v [k+3/2]
i
⃗v [k+1/2]
i
=⃗r [k]
i
+∆t⃗v [k+1/2]
i
=⃗v [k+1/2]
i +∆t⃗a i (⃗r [k+1] )
In addition, it is accurate to second order, meaning that the error
is
O(∆t 3 )
per step, and requires very little storage.
A drawback of the leapfrog is that velocities are a half-step out
of sync with positions; this can be avoided as follows:
⃗r [k+1]
i
⃗v [k+1]
i
=⃗v [k]
i
=⃗r [k]
i
=⃗v [k+1/2]
i
+ ∆t
2 ⃗a i(⃗r [k] )
+∆t⃗v [k+1/2]
i
+ ∆t
2 ⃗a i(⃗r [k+1] )
This formulation introduces a one-time error of
otherwise equivalent to the standard leapfrog.
O(∆t 2 )
but is

Individual Time Steps?
Leapfrog becomes inaccurate if ∆t is not constant
and identical for all bodies. This seems inefficient.
However, the symplectic properties of the leapfrog
give it much more stability than most integrators.
Algorithms in which ∆t is determined by current
conditions are not reversible. Symmetrizing the
time step between endpoints t and t + ∆t works
but imposes a significant overhead (Hut et al. 1995).
A 4 th order symplectic scheme allowing individual
and adaptive time-steps is now available (Farr &
Bertschinger 2007).
Springel (2005)

Errors and Relaxation
N-body simulations diverge from exact
solutions of CBE and PE for several reasons:
1. Roundoff errors.
2. Truncation in time stepping.
3. Force calculation approximations.
4. Density field smoothing.
5. Relaxation due to finite N.
“An Introduction to Error Analysis”, John R. Taylor
In theory, these effects can all be controlled — at a price. Error
#1 is seldom an issue, while errors #2 and #3 are easily limited.
Smoothing and relaxation are harder to balance; high resolution
demands shorter timesteps and more bodies.
Finally, all N-body systems with N > 2 are potentially chaotic,
while the role of chaos in real galaxies is unclear.

Parameter Choices
The number of bodies
N
is the key parameter:
— 2-body relaxation time: t r ≃ Nt c /8ln(R /ε)
— Monte-Carlo errors: O(N −1/2 )
Maximum duration of simulation must be . t ≪ t r
Typical errors in acceleration should be |δa/a| N −1/2 .
Global energy should be conserved to |δE/E| N −1/2 .
Smoothing length is typically R N −1/2 < ε < R N −1/3 .
Leapfrog time-step should be ∆t 0.03t min ≃ 0.09(Gρ max ) −1/2 .
WARNING: these rules are not definitive. Tests with different
parameter values are useful; a skeptical attitude is advised!

Introduction to Smoothed Particle Hydrodynamics
Fluid equations in conservation form:
mass:
momentum:
∂ρ
∂t + ∇ · (ρ⃗v) = 0
∂⃗v
∂t + (⃗v · ∇)⃗v = −∇Φ + 1 ρ ∇P
energy or
entropy:
∂u
∂t + (⃗v · ∇)u = −P ∇ ·⃗v + ˙u
ρ
∂a
∂t + (⃗v · ∇)a = (γ − 1)ρ1−γ ˙u
Equation of state (ideal gas):
P = (γ − 1)ρu
P = a(S)ρ γ

ρ(⃗r),⃗v(⃗r), u(⃗r), a(⃗r) → {(m i ,⃗r i ,⃗v i , u i , a i ) | i = 1,...,N}
d⃗r i
dt =⃗v i
du i
dt = (
− P ρ ∇ ·⃗v )
i
SPH Formalism
Particle representation (c.f. N-body):
Density estimate uses smoothing kernel W(⃗x,h) with scale h :
N
ρ(⃗r) ≃ ∑m i W(⃗r −⃗r i ,h)
i
R
where d⃗xW(⃗x,h) = 1 ; estimates of gradients become sums
involving gradients of W(⃗x,h) .
Dynamical equations:
d⃗v i
dt = (−∇Φ) i + (
− 1 ρ ∇P )
+ ˙u i + ˙u visc
i
da i
dt
i
+⃗a visc
i
= (γ − 1)ρ1−γ i
( ˙u i + ˙u visc
i )

Comments
1. The smoothing kernel W(⃗x,h) has compact support, so only
nearby bodies are included in the sums. Most SPH codes adapt
the smoothing length h to the local particle density.
2. Adaptive timesteps are generally necessary to satisfy the
Courant condition; most SPH integrators are not symplectic.
3. Artificial viscosity is required to keep particles from streaming
through shocks. The best formulation is not entirely clear.
4. SPH is often criticized as a poor approximation to proper gas
dynamics. However, the ISM is much more complex than an ideal
gas. In the context of galaxy-scale simulations, momentum and
energy conservation may be all we can expect of a code.