Etudes et évaluation de processus océaniques par des hiérarchies ...

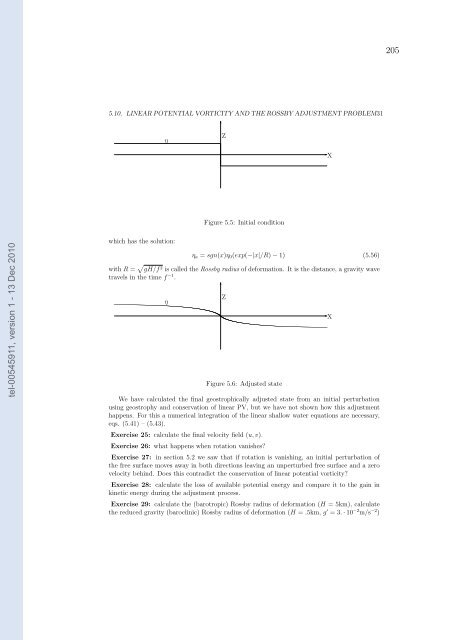
205
5.10. LINEAR POTENTIAL VORTICITY AND THE ROSSBY ADJUSTMENT PROBLEM31
✻
η
Z
✲ X
Figure 5.5: Initial condition
tel-00545911, version 1 - 13 Dec 2010
which has the solution:
η a = sgn(x)η 0 (exp(−|x|/R) − 1) (5.56)
with R = √ gH/f 2 is called the Rossby radius of deformation. It is the distance, a gravity wave
travels in the time f −1 .
η
✻
Z
Figure 5.6: Adjusted state
We have calculated the final geostrophically adjusted state from an initial perturbation
using geostrophy and conservation of linear PV, but we have not shown how this adjustment
happens. For this a numerical integration of the linear shallow water equations are necessary,
eqs. (5.41) – (5.43).
Exercise 25: calculate the final velocity field (u,v).
Exercise 26: what happens when rotation vanishes?
Exercise 27: in section 5.2 we saw that if rotation is vanishing, an initial perturbation of
the free surface moves away in both directions leaving an unperturbed free surface and a zero
velocity behind. Does this contradict the conservation of linear potential vorticity?
Exercise 28: calculate the loss of available potential energy and compare it to the gain in
kinetic energy during the adjustment process.
Exercise 29: calculate the (barotropic) Rossby radius of deformation (H = 5km), calculate
the reduced gravity (baroclinic) Rossby radius of deformation (H = .5km, g ′ = 3. · 10 −2 m/s −2 )
✲ X