Etudes et évaluation de processus océaniques par des hiérarchies ...

4.7. ON THE BASIC STRUCTURE OF OCEANIC GRAVITY CURRENTS 139
Ocean Dynamics (2009) 59:551–563 559
tel-00545911, version 1 - 13 Dec 2010
√
νg
′2
/(2 f 3 ). The boundary conditions at the lower and
upper ends of the vein are important. At the downslope
side end of the vein (point A), which is moving downward,
the boundary condition is ∂ x h(A) = 0, which is
automatically satisfied for the freely evolving height. At
the upper end (point B), there is no flux if the surface
is level, that is, ∂ x h(B) = − tan α, which I impose at the
upper end of the vein. This leads automatically to the
right detrainment of the integrated thickness ∫ B
A hdx,
through the friction layer, which is
κ H ∂ x h(B) = −κ H tan α = − δg′ tan α (3)
2 f
Please note that there is no free parameter in the
simple model, so no adjustment is possible! The finding
that geostrophic dynamics subject to Ekman bottom
friction can be described by a heat equation is also
used by Gill (1982, Chap. 9.12, Eq. 9.12.8), MacCready
(1994) and others. To the best of my knowledge, it has,
so far, not been applied to gravity current dynamics.
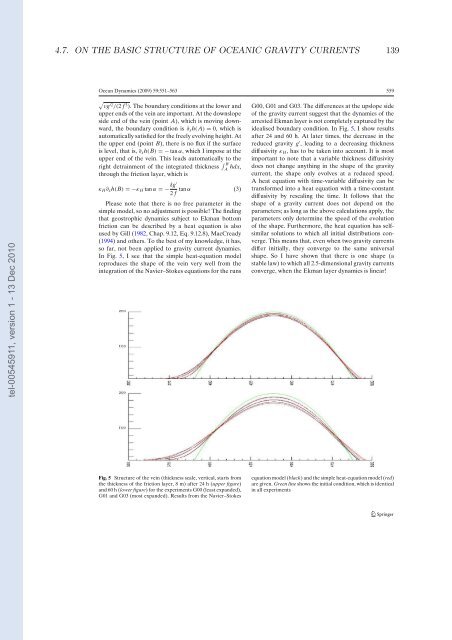
In Fig. 5, I see that the simple heat-equation model
reproduces the shape of the vein very well from the
integration of the Navier–Stokes equations for the runs
G00, G01 and G03. The differences at the upslope side
of the gravity current suggest that the dynamics of the
arrested Ekman layer is not completely captured by the
idealised boundary condition. In Fig. 5, I show results
after 24 and 60 h. At later times, the decrease in the
reduced gravity g ′ , leading to a decreasing thickness
diffusivity κ H , has to be taken into account. It is most
important to note that a variable thickness diffusivity
does not change anything in the shape of the gravity
current, the shape only evolves at a reduced speed.
A heat equation with time-variable diffusivity can be
transformed into a heat equation with a time-constant
diffusivity by rescaling the time. It follows that the
shape of a gravity current does not depend on the
parameters; as long as the above calculations apply, the
parameters only determine the speed of the evolution
of the shape. Furthermore, the heat equation has selfsimilar
solutions to which all initial distributions converge.
This means that, even when two gravity currents
differ initially, they converge to the same universal
shape. So I have shown that there is one shape (a
stable law) to which all 2.5-dimensional gravity currents
converge, when the Ekman layer dynamics is linear!
Fig. 5 Structure of the vein (thickness scale, vertical, starts from
the thickness of the friction layer, 8 m) after 24 h (upper figure)
and 60 h (lower figure) for the experiments G00 (least expanded),
G01 and G03 (most expanded). Results from the Navier–Stokes
equation model (black) and the simple heat-equation model (red)
are given. Green line shows the initial condition, which is identical
in all experiments