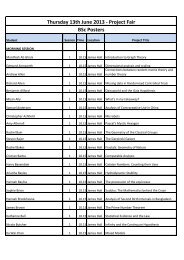
Denoising and Analysis of 2D NMR Spectra for Metabolomic ...
Denoising and Analysis of 2D NMR Spectra for Metabolomic ...
Denoising and Analysis of 2D NMR Spectra for Metabolomic ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong><br />
<strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Simon Poulding<br />
Dissertation submitted <strong>for</strong> the MSc in Mathematics with Modern Applications,<br />
Department <strong>of</strong> Mathematics, University <strong>of</strong> York, UK.<br />
August 2006
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Acknowledgements<br />
I would like to acknowledge the support <strong>and</strong> assistance <strong>of</strong> the following: Dr Julie Wilson <strong>for</strong><br />
her extensive input, suggestions <strong>and</strong> comments, as well as the provision <strong>of</strong> hardware <strong>and</strong> s<strong>of</strong>tware;<br />
Dr Adrian Charlton <strong>and</strong> Dr James Donarski <strong>of</strong> the Central Science Laboratories <strong>for</strong> the acquisition<br />
<strong>and</strong> provision <strong>of</strong> <strong>NMR</strong> data sets, demonstrating the principles <strong>of</strong> <strong>NMR</strong> spectroscopy, assisting with<br />
the use <strong>of</strong> Bruker Topspin s<strong>of</strong>tware, <strong>and</strong> commenting on the objectives <strong>and</strong> results; <strong>and</strong> Dr Jason<br />
Levesley <strong>for</strong> his guidance on the content <strong>and</strong> structure <strong>of</strong> the dissertation.<br />
1
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Contents<br />
Acknowledgements 1<br />
1. Introduction 4<br />
1.1. Project Objectives 4<br />
1.2. Document Structure 4<br />
2. Statistical <strong>Analysis</strong> <strong>and</strong> Reduction <strong>of</strong> t1-Noise 5<br />
2.1. The Phase-Cycled HSQC Experiment <strong>and</strong> Sources <strong>of</strong> t1-Noise 5<br />
2.2. Initial <strong>Analysis</strong> 6<br />
2.3. Noise Separation 9<br />
2.4. Correlation <strong>of</strong> t1-Noise Traces 15<br />
2.5. Complex Correlation <strong>of</strong> t1-Noise Traces 17<br />
2.6. <strong>Denoising</strong> Algorithm 24<br />
2.7. Results <strong>and</strong> Discussion 26<br />
2.8. Comparison to Other t1-Noise Reduction Techniques 31<br />
3. Automated Peak Picking Using a Genetic Algorithm 33<br />
3.1. Peak Shape 33<br />
3.2. Peak Width 33<br />
3.3. Peak Fit Metric 34<br />
3.4. A Priori Knowledge Encapsulated in the Genetic Algorithm 34<br />
3.5. Suitability <strong>of</strong> Genetic Algorithms As The Optimisation Technique 36<br />
3.6. Identification <strong>of</strong> Convoluted Peak Regions 38<br />
3.7. Genetic Algorithm Representation, Operators <strong>and</strong> Objective Function 38<br />
3.8. Technical Implementation 41<br />
3.9. Results <strong>and</strong> Discussion 41<br />
4. Combined <strong>Denoising</strong> <strong>and</strong> Peak Picking Process 46<br />
4.1. Implementation Overview 46<br />
4.2. Processing Steps 46<br />
4.3. Results <strong>and</strong> Discussion 48<br />
5. Two-Dimensional Adaptive Binning 52<br />
5.1. Overview <strong>of</strong> One-Dimensional Adaptive Binning 52<br />
5.2. Objective <strong>for</strong> Two-Dimensional Adaptive Binning Research 52<br />
5.3. Two-Dimensional Adaptive Binning Method 52<br />
5.4. Results <strong>and</strong> Discussion 53<br />
6. Conclusion 57<br />
6.1. Evaluation <strong>of</strong> Project Objectives 57<br />
6.2. Further Investigation 57<br />
Appendix A. Pulse Fourier Trans<strong>for</strong>m <strong>NMR</strong> 59<br />
A.1. Nuclear Magnetic Moment 59<br />
A.2. Pulse <strong>NMR</strong> 60<br />
A.3. Relaxation 62<br />
A.4. Chemical Shift 62<br />
A.5. Spin-Spin Coupling 63<br />
A.6. Signal Detection <strong>and</strong> Processing 63<br />
A.7. Multi-Dimensional <strong>NMR</strong> 65<br />
A.8. <strong>NMR</strong> Sensitivity 67<br />
Appendix B. Wavelet <strong>Analysis</strong> 69<br />
B.1. Continuous Wavelet Trans<strong>for</strong>m 69<br />
B.2. Discrete Wavelet Trans<strong>for</strong>m 71<br />
B.3. Scaling Functions 74<br />
B.4. Fast Wavelet Trans<strong>for</strong>m 75<br />
B.5. Pyramid Algorithm 77<br />
B.6. Wavelet Construction <strong>and</strong> Families 80<br />
B.7. <strong>Denoising</strong> <strong>and</strong> Smoothing 82<br />
2
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
B.8. Non-Decimating (Translation Invariant) Trans<strong>for</strong>m 84<br />
B.9. Two-Dimensional Discrete Wavelet Trans<strong>for</strong>ms 85<br />
Appendix C. Genetic Algorithm Overview 87<br />
C.1. Evolutionary Algorithms 87<br />
C.2. Steady-State Genetic Algorithms 87<br />
C.3. Representation 88<br />
C.4. Operators 88<br />
C.5. Objective Function 88<br />
Appendix D. Experimental Methods 89<br />
Appendix E. Code Structure 90<br />
E.1. <strong>Denoising</strong> <strong>and</strong> Peak Picking 90<br />
E.2. Two-Dimensional Adaptive Binning 91<br />
References 92<br />
3
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
1. Introduction<br />
1.1. Project Objectives. The analysis <strong>of</strong> the metabolome—the set <strong>of</strong> the chemical compounds,<br />
or metabolites, synthesised by a cell[10]—can provide extremely useful in<strong>for</strong>mation about biological<br />
samples. For example, the comparison <strong>of</strong> metabolic pr<strong>of</strong>iles can elucidate in<strong>for</strong>mation about gene<br />
function[19], distinguish samples from different genetic lines[6, 7], <strong>and</strong> identify marker metabolites<br />
<strong>for</strong> disease states[3].<br />
Nuclear Magnetic Resonance (<strong>NMR</strong>) is one <strong>of</strong> the techniques used <strong>for</strong> analysing the metabolome.<br />
It measures the magnetic resonance frequencies <strong>of</strong> particular nuclei in a sample, <strong>and</strong> since the<br />
resonance frequency is modified by the chemical environment <strong>of</strong> the nucleus in question[9], each<br />
metabolite has a different, yet characteristic, set <strong>of</strong> resonance frequencies. The <strong>NMR</strong> spectrum <strong>of</strong><br />
a sample thus provides in<strong>for</strong>mation about its metabolic pr<strong>of</strong>ile.<br />
Two-dimensional <strong>NMR</strong> experiments analyse the relationship between two different nuclei in<br />
metabolites, <strong>and</strong> the extra dimensionality in the data, compared to one-dimensional experiments,<br />
can further distinguish metabolites. Since metabolites are organic molecules, an appropriate twodimensional<br />
<strong>NMR</strong> experiment <strong>for</strong> metabolomic pr<strong>of</strong>iling is 1 H– 13 C Heteronuclear Single Quantum<br />
Coherence (HSQC): it identifies hydrogen <strong>and</strong> carbon atoms connected by a single bond.<br />
However, the most sensitive type <strong>of</strong> HSQC experiments—suitable <strong>for</strong> detecting the very low<br />
concentrations <strong>of</strong> some compounds in metabolomic samples—suffer from artefacts called t1-noise<br />
that can obscure some <strong>of</strong> the peaks in the sample <strong>and</strong> hinder peak identification[22, 17]. In<br />
addition, the process <strong>of</strong> picking peaks in the spectrum, <strong>and</strong> especially <strong>of</strong> distinguishing small<br />
peaks from both the t1-noise <strong>and</strong> general noise, is relatively manual <strong>and</strong> relies on the knowledge <strong>of</strong><br />
the experimenter. This makes the process time-consuming <strong>and</strong> open to subjective interpretation.<br />
These problems motivate the first two objectives <strong>of</strong> the project. Firstly, to explore techniques<br />
<strong>for</strong> the reduction <strong>of</strong> the t1-noise through analysis <strong>of</strong> the <strong>2D</strong> <strong>NMR</strong> data set. The second is to<br />
automate the picking <strong>of</strong> peaks <strong>and</strong> distinguishing peaks from noise artefacts.<br />
A further objective concerns the comparison <strong>of</strong> metabolic pr<strong>of</strong>iles. The frequencies <strong>of</strong> peaks in<br />
an <strong>NMR</strong> spectrum can change depending on factors such as the pH or temperature <strong>of</strong> the sample,<br />
<strong>and</strong> the shift in frequency is different <strong>for</strong> each peak[14]. There<strong>for</strong>e, direct comparison <strong>of</strong> spectral<br />
peaks by matching frequency coordinates is not appropriate. One alternative is to use ‘binning’:<br />
the spectrum is partitioned into equal-sized intervals <strong>and</strong> the total spectral intensity within each<br />
bin is calculated. Pr<strong>of</strong>iles are then compared using the total intensities <strong>for</strong> corresponding bins,<br />
with assumption that shifted peaks are contained within the same bin (<strong>for</strong> example, as used in<br />
[11]). However, binning does not take account <strong>of</strong> the actual distribution <strong>of</strong> peaks in the spectrum,<br />
<strong>and</strong> so, <strong>for</strong> example, the shifting <strong>of</strong> peaks located on the bin boundaries can limit its effectiveness.<br />
A refinement <strong>of</strong> binning, termed ‘adaptive binning’ <strong>and</strong> described in [6], has proved successful <strong>for</strong><br />
the comparison <strong>of</strong> one-dimensional <strong>NMR</strong> spectra <strong>of</strong> metabolic samples. This method, leveraging<br />
wavelet techniques, assigns both bin location <strong>and</strong> size based on the distribution <strong>of</strong> peaks across<br />
a number <strong>of</strong> experimental spectra. The third objective in this project is to assess the use <strong>of</strong> this<br />
technique on two-dimensional <strong>NMR</strong> spectra.<br />
1.2. Document Structure. Subsequent sections <strong>of</strong> this document describe:<br />
• the reduction <strong>of</strong> t1-noise by the statistical analysis <strong>of</strong> <strong>2D</strong> data sets;<br />
• automated peak picking;<br />
• the processing, incorporating both the above steps, to establish spectra free <strong>of</strong> noise <strong>and</strong><br />
artefacts;<br />
• adaptive binning in <strong>2D</strong> <strong>NMR</strong> spectra.<br />
The theoretical background <strong>and</strong> practical application <strong>of</strong> the <strong>NMR</strong> experiments used to acquire<br />
the <strong>2D</strong> <strong>NMR</strong> spectra are summarised in Appendix A. Appendix B reviews the mathematics <strong>of</strong> the<br />
wavelet analysis techniques used in this project. Further appendices provide a short overview <strong>of</strong><br />
genetic algorithms (used here to implement automated peak picking); describe the experimental<br />
methods used to acquire <strong>and</strong> process the <strong>NMR</strong> data sets; <strong>and</strong> outline the structure <strong>of</strong> the code<br />
created <strong>for</strong> this project.<br />
4
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
2. Statistical <strong>Analysis</strong> <strong>and</strong> Reduction <strong>of</strong> t1-Noise<br />
As discussed in the introduction, the <strong>2D</strong> HSQC <strong>NMR</strong> experiment <strong>for</strong> the isotopes 1 H <strong>and</strong> 13 C<br />
is a powerful technique <strong>for</strong> pr<strong>of</strong>iling the metabolome. The phase-cycled version <strong>of</strong> HSQC is more<br />
sensitive than alternative <strong>of</strong> method <strong>of</strong> gradient-selection [22] <strong>and</strong> there<strong>for</strong>e better <strong>for</strong> the detection<br />
<strong>of</strong> metabolites at low concentration. However, phase-cycled HSQC suffers from artefacts known<br />
as t1-noise that can hinder the identification <strong>of</strong> peaks.<br />
This section describes the sources <strong>of</strong> t1-noise in phase-cycled HSQC, describes analysis <strong>of</strong> the<br />
structure <strong>of</strong> the noise, <strong>and</strong>—based on the results <strong>of</strong> the analysis—proposes an algorithm <strong>for</strong> noise<br />
reduction through processing <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> data sets.<br />
2.1. The Phase-Cycled HSQC Experiment <strong>and</strong> Sources <strong>of</strong> t1-Noise. An overview <strong>of</strong> twodimensional<br />
<strong>NMR</strong> is given in appendix A. The <strong>2D</strong> HSQC experiment uses a specific pulse sequence<br />
that identifies the resonance frequencies <strong>of</strong> 1 H <strong>and</strong> 13 C nuclei where the atoms are connected by a<br />
single chemical bond. A series <strong>of</strong> FIDs (see section A.6) are acquired that measure the resonance<br />
frequency <strong>of</strong> 1 H nuclei. For each FID, a timing parameter, t1, in the pulse sequence is changed,<br />
<strong>and</strong> the nature <strong>of</strong> the sequence is such that the phase <strong>of</strong> each <strong>of</strong> the 1 H frequencies in the FID<br />
‘evolves’ with an angular frequency that is the resonance frequency <strong>of</strong> the 13 C nuclei to which<br />
is attached via a single bond. The <strong>2D</strong> frequency spectrum derived from processing the FIDs is<br />
plotted with the 1 H frequency on the horizontal F2 axis, <strong>and</strong> 13 C on the vertical F1 axis.<br />
In naturally occurring carbon, 99% <strong>of</strong> the atoms are the isotope 12 C <strong>and</strong> only 1% are 13 C<br />
[14, 13]. Since 12 C is not a magnetic nucleus (see section A.1.1), it has no resonance frequency<br />
<strong>and</strong> there<strong>for</strong>e provides no additional in<strong>for</strong>mation in a <strong>2D</strong> HSQC experiment. Owing to its high<br />
abundance, the resonance signals detected from 1 H bonded to 12 C would overwhelm the desired<br />
signals from the 1 H– 13 C bonds <strong>and</strong> so are suppressed by the experimental procedure. In phasecycled<br />
HSQC, two FIDs are acquired at each t1 value with part <strong>of</strong> the pulse sequence modified <strong>for</strong><br />
one <strong>of</strong> the FIDs. The change in the pulse sequence reverses the phase <strong>of</strong> the signal resulting from<br />
1 H– 12 C bonds, but leaves the 1 H– 13 C signal unchanged. Adding the two signals together leaves<br />
only the desired 1 H– 13 C resonance frequencies[21].<br />
However, instrumental imperfections result in incomplete cancellation <strong>of</strong> the undesired 12 C<br />
signals. These imperfections change on each FID acquisition, <strong>and</strong> include[17]:<br />
• inconsistent rotation <strong>of</strong> the bulk magnetic moment caused by the radio frequency pulse,<br />
owing to the variation in field strength or pulse timing (see section A.2.2);<br />
• inconsistent phase <strong>of</strong> the radio frequency pulse;<br />
• inconsistent timing between the acquisition <strong>of</strong> successive FIDs.<br />
(These are distinguished from other instrumental imperfections that show variation both during<br />
the acquisition <strong>of</strong> a single FID as well as between successive acquisitions.)<br />
After the first Fourier trans<strong>for</strong>m in the F2 axis (see section A.7), the change in peak phase<br />
angle with t1 includes components resulting from the incomplete cancellation <strong>of</strong> unwanted signals.<br />
These components have a wide range <strong>of</strong> frequencies, <strong>and</strong> so after the second Fourier trans<strong>for</strong>m<br />
are seen as a ridge <strong>of</strong> signal intensity parallel to the F1 axis. The noise occurs at F2 resonance<br />
frequency <strong>of</strong> the 1 H nucleus in the 1 H– 12 C bond which will coincide with the F2 frequency <strong>of</strong> the<br />
1 H– 13 C bond, so the t1-noise ridge is associated with large peaks in the spectrum.<br />
An example <strong>of</strong> t1-noise in an HSQC spectrum is shown in Figure 1. The experimental method<br />
<strong>for</strong> this, <strong>and</strong> the other spectra used in this project, are described in appendix D.<br />
Note the spectrum contains other sources <strong>of</strong> noise, although in the HSQC spectra used in this<br />
project they are less intense than the t1-noise. One <strong>for</strong>m occurs uni<strong>for</strong>mly at all frequencies <strong>and</strong><br />
is termed thermal noise. It is also instrumental in nature, <strong>and</strong> caused by background noise in<br />
the receiver coil[17]. In some cases, noise ridges parallel to the F2 axis can occur: this ‘t2-noise’<br />
results from limitations <strong>of</strong> the signal processing hardware[17].<br />
An alternative to phase-cycling is gradient-selection where the stable magnetic field, B0, varies<br />
steadily along the length <strong>of</strong> the sample. However, the gradient-selected HSQC experiment is √ 2<br />
less sensitive than the equivalent phase-cycled version, <strong>and</strong> the sensitivity difference is larger when<br />
5
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Figure 1. Example <strong>of</strong> t1-noise in an HSQC spectrum <strong>of</strong> sucrose. (Only a small<br />
section <strong>of</strong> the F2 range is shown.) The t1-noise is seen as ‘ridges’ parallel to the<br />
F1 axis at the F2 frequencies <strong>of</strong> intense peaks.<br />
using the st<strong>and</strong>ard experimental techniques[22]. This motivates the desire to minimise the t1-noise<br />
in phased-cycled HSQC.<br />
2.2. Initial <strong>Analysis</strong>. The approach taken is to analyse the structure <strong>of</strong> the t1-noise in order<br />
to identify features that distinguish the noise from peaks (particularly small peaks) that may be<br />
convoluted with the noise. The analysis <strong>of</strong> the noise structure is described in this section.<br />
2.2.1. Data. For the initial analysis, the real–real spectrum—i.e. the real part <strong>of</strong> the Fourier<br />
trans<strong>for</strong>m in both dimensions corresponding to the absorption signal (see section A.6.5)—was<br />
downloaded as a text file from the Bruker Topspin s<strong>of</strong>tware used to acquire <strong>and</strong> process the<br />
spectrum. A C ++ MEX function was used to load this data into matlab as a matrix.<br />
2.2.2. Visual Inspection. The structure <strong>of</strong> the t1-noise shown in Figure 1 is typical <strong>of</strong> the ridges<br />
seen across a number <strong>of</strong> spectra. Firstly, periodic behaviour is evident along the direction parallel<br />
to the F1 axis. Secondly, there are usually two distinct lines <strong>of</strong> peaks in each ridge either side <strong>of</strong><br />
a central ‘trough’ where the t1-noise has less intensity. These lines are termed noise maxima lines<br />
in this project to avoid confusion with the terminology ‘peak’.<br />
Figure 2 shows an F1 trace—a 1D section through a <strong>2D</strong> spectrum parallel to the F1 axis at a<br />
constant F2 value—along a maxima line in a t1-noise ridge <strong>of</strong> a HSQC glycine spectrum. (The<br />
glycine spectrum is used <strong>for</strong> this <strong>and</strong> the next figure since it shows a single intense peak <strong>and</strong> so<br />
the associated t1-noise ridge is not affected by equivalent ridges from any nearby peaks.) The plot<br />
<strong>of</strong> the trace intensity also suggests that the noise contains periodic components.<br />
Figure 3 shows the interquartile range (iqr) <strong>of</strong> F1 traces <strong>for</strong> a range <strong>of</strong> F2 frequencies across the<br />
same glycine t1-noise ridge. The iqr is used here as an estimate <strong>of</strong> the noise intensity (this concept<br />
is developed in section 2.3.2) <strong>and</strong> confirms the presence <strong>of</strong> the two maxima lines in the ridge.<br />
6
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Intensity<br />
0.5<br />
−0.5<br />
−1<br />
x 106<br />
1<br />
0<br />
140<br />
120<br />
100<br />
80<br />
F 1 ( 13 C) / ppm<br />
Figure 2. F1 trace through an HSQC spectrum <strong>of</strong> glycine at F2 = 3.447 ppm<br />
showing the periodic components <strong>of</strong> the t1-noise. The peak associated with this<br />
ridge is at F1 = 41.30 ppm; it reaches an intensity <strong>of</strong> 6.6 ×10 6 <strong>and</strong> so is truncated<br />
in this plot.<br />
iqr(Intensity)<br />
2.5<br />
1.5<br />
0.5<br />
x 105<br />
3<br />
2<br />
1<br />
0<br />
3.55<br />
3.5<br />
3.45<br />
F 2 ( 1 H) / ppm<br />
Figure 3. Interquartile range <strong>of</strong> the intensity along F1 traces at F2 frequencies<br />
across the t1-noise ridge in an HSQC spectrum <strong>of</strong> glycine.<br />
2.2.3. Fourier <strong>Analysis</strong>. The periodic components indicated above suggest that Fourier analysis<br />
<strong>of</strong> the trace along t1-noise ridges may yield in<strong>for</strong>mation about the structure <strong>of</strong> the noise.<br />
An <strong>NMR</strong> spectrum shows intensity as a function <strong>of</strong> frequency. Here, Fourier analysis is used<br />
to quantify periodic components as the <strong>NMR</strong> resonance frequency changes, so the trace is being<br />
considered as if it were a signal that varies with time. For this analysis, an arbitrary ‘time’ unit<br />
<strong>of</strong> one is assumed between each discrete frequency datum in the trace.<br />
Figure 4(a) shows the power spectrum <strong>for</strong> the section <strong>of</strong> the t1-noise trace shown in figure 2<br />
at higher frequencies than the peak, but not including the peak itself. This, <strong>and</strong> the other power<br />
spectra in this figure, were taken using a trace along the higher frequency noise maxima line <strong>of</strong><br />
each t1-noise ridge. Part (b) <strong>of</strong> the figure shows the power spectra <strong>for</strong> similar trace sections in<br />
the sucrose spectrum shown in Figure 1 corresponding to the two most intense peaks <strong>and</strong> another<br />
peak at higher F2 frequency. The amplitude <strong>of</strong> the noise differs <strong>for</strong> each peak, so the energy is<br />
normalised, using the mean energy <strong>of</strong> each, in order to facilitate comparison. Part (c) shows the<br />
power spectra <strong>for</strong> two sections <strong>of</strong> the t1-noise trace associated with the most intense peak in the<br />
sucrose HSQC spectrum, one section at F1 frequencies higher than the peak, the other, lower.<br />
The power spectra show concentration <strong>of</strong> the energy at particular periods in the t1-noise, confirming<br />
the periodicity. The are a number <strong>of</strong> prominent periods, <strong>and</strong> there is a significant energy<br />
at a range <strong>of</strong> periods. Part (b) <strong>of</strong> the figure shows significant similarity in power spectra <strong>for</strong> the<br />
different t1-noise ridges in the same HSQC spectra, when considered over the same range <strong>of</strong> F1<br />
7<br />
60<br />
3.4<br />
40<br />
20<br />
3.35
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
(c)<br />
Energy<br />
Normalised Energy<br />
Energy<br />
1.5<br />
1<br />
0.5<br />
x 1014<br />
2<br />
0<br />
0 5 10 15 20 25 30 35 40 45 50<br />
30<br />
25<br />
20<br />
15<br />
10<br />
5<br />
F 2 = 5.302 ppm<br />
F 2 = 3.707 ppm<br />
F 2 = 3.5637 ppm<br />
Period<br />
0<br />
0 5 10 15 20 25 30 35 40 45 50<br />
x 1013<br />
4<br />
3<br />
2<br />
1<br />
F 1 = 157.0 − 105.4 ppm<br />
F 1 = 55.38 − 3.768 ppm<br />
Period<br />
0<br />
0 5 10 15 20 25 30 35 40 45 50<br />
Period<br />
Figure 4. (a) Power spectrum <strong>of</strong> a section <strong>of</strong> the t1-noise trace in a glycine<br />
HQSC spectrum (F2 = 3.447 ppm, F1 = 157.0 − 97.60 ppm). (b) Normalised<br />
power spectra <strong>of</strong> sections (F1 = 157.0 − 97.60 ppm) <strong>of</strong> t1-noise traces <strong>of</strong> a sucrose<br />
HSQC spectrum. (c) Power spectra <strong>for</strong> sections <strong>of</strong> the trace (F2 = 3.707 ppm) at<br />
frequencies higher (F1 = 157.0 − 97.60 ppm) <strong>and</strong> lower (F1 = 55.38 − 3.768 ppm)<br />
than associated intense peak in the same sucrose spectrum.<br />
frequencies. By comparing parts (a) <strong>and</strong> (b), taken over the same F1 range, it can be seen that<br />
the frequency components <strong>of</strong> the noise differ between spectra. 1 Part (c) <strong>of</strong> the figure shows that<br />
the frequency components differ between sections <strong>of</strong> the same t1-noise ridge.<br />
2.2.4. Continuous Wavelet Trans<strong>for</strong>m. The possible change in periodic behaviour with location<br />
motivates the use the Continuous Wavelet Trans<strong>for</strong>m (CWT), as described in section B.1.<br />
1 The two spectra were taken during the same experimental run with the same spectrometer <strong>and</strong> processing<br />
configuration.<br />
8
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Scale (a)<br />
55<br />
52<br />
49<br />
46<br />
43<br />
40<br />
37<br />
34<br />
31<br />
28<br />
25<br />
22<br />
19<br />
16<br />
13<br />
10<br />
7<br />
4<br />
1<br />
100 200 300<br />
Position (b)<br />
400 500 600<br />
Figure 5. Pseudocolour plot <strong>of</strong> the Continuous Wavelet Trans<strong>for</strong>m (using the<br />
Mexican Hat wavelet) <strong>of</strong> a trace through an HSQC spectrum <strong>of</strong> glycine (F2 =<br />
3.447 ppm, F1 = 157.0 − 97.60 ppm). Lighter shades correspond to the largest<br />
absolute values <strong>of</strong> the trans<strong>for</strong>m.<br />
The CWT was per<strong>for</strong>med using the ‘Mexican Hat’ wavelet (section B.1.6). This wavelet function<br />
was chosen <strong>for</strong> the CWT since it is symmetrical <strong>and</strong> has a shape (see Figure 39) that is similar<br />
to the peaks in the noise, both <strong>of</strong> which make the interpretation <strong>of</strong> the wavelet coefficients more<br />
straight<strong>for</strong>ward. Figure 5 shows a pseudocolour plot <strong>of</strong> the CWT <strong>of</strong> a t1-noise trace.<br />
By comparison with the CWT <strong>of</strong> a simple periodic signal given in Figure 40, it can be seen<br />
that the CWT <strong>of</strong> the t1-noise trace provides evidence <strong>of</strong> periodic components in the signal. The<br />
presence <strong>of</strong> maxima (the lightest shades) at a range <strong>of</strong> scale values suggests that signal contains<br />
a number <strong>of</strong> periodic components at different frequencies. Although there is significant periodic<br />
behaviour with position, such as regularly alternating b<strong>and</strong>s <strong>of</strong> light <strong>and</strong> dark, the nature <strong>of</strong> this<br />
behaviour does vary across the CWT plot, confirming that the frequency components are localised.<br />
2.2.5. Conclusion. Both Fourier analysis <strong>and</strong> the Continuous Wavelet Trans<strong>for</strong>m show that the<br />
t1-noise signal has a relatively large number <strong>of</strong> periodic components <strong>and</strong> that the nature <strong>of</strong> the components<br />
changes with location along the the signal. Both the number <strong>of</strong> components <strong>and</strong> localised<br />
behaviour would make it difficult to accurately isolate the noise from small peaks convoluted with<br />
the t1-noise ridge.<br />
However, the similar nature <strong>of</strong> the power spectra shown in Figure 4(b) indicates sections <strong>of</strong> the<br />
t1-noise ridges covering the same F1 frequency ranges do have very similar structure, even when<br />
the ridges are far from one another in the F2 dimension. This suggests analysis <strong>of</strong> the correlation<br />
between t1-noise traces would be useful.<br />
2.3. Noise Separation. In the initial investigations using Fourier <strong>and</strong> wavelet analysis, sections<br />
<strong>of</strong> the trace were used that did not contain ‘genuine’ spectral peaks as they would have added spurious<br />
components to the signal. Measurement <strong>of</strong> correlation would be similarly affected, especially<br />
if a large peak were present in one trace <strong>and</strong> not the other.<br />
However, the <strong>2D</strong> spectra <strong>of</strong> metabolic samples potentially have genuine peaks at many locations,<br />
<strong>and</strong> so any technique to reduce the noise must h<strong>and</strong>le the presence <strong>of</strong> peaks, rather than restrict<br />
its operation to sections <strong>of</strong> the spectrum free <strong>of</strong> peaks. For this reason, <strong>and</strong> to allow more accurate<br />
correlation calculations based on the entire length <strong>of</strong> the trace rather than small peak-free sections,<br />
the next step <strong>of</strong> the analysis is to separate the noise from the genuine peaks.<br />
Note that the purpose is more accurately stated as the separation <strong>of</strong> components <strong>of</strong> the same<br />
amplitude as the noise from the significantly larger genuine peaks. Noise separation is unlikely to<br />
be able to distinguish small genuine peaks convoluted with the noise from the noise itself <strong>and</strong> so<br />
these small peaks will be appear as part <strong>of</strong> the separate noise signal.<br />
2.3.1. Noise Distribution. The noise separation techniques use a threshold to distinguish between<br />
noise <strong>and</strong> peak signal components. An accurate determination <strong>of</strong> the appropriate threshold depends<br />
upon an underst<strong>and</strong>ing <strong>of</strong> the distribution <strong>of</strong> the noise values.<br />
9
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Count<br />
12000<br />
10000<br />
8000<br />
6000<br />
4000<br />
2000<br />
0<br />
−4 −3 −2 −1 0 1 2 3 4<br />
Normalised Intensity<br />
0.999<br />
0.997<br />
0.99<br />
0.98<br />
0.95<br />
0.90<br />
0.75<br />
0.50<br />
0.25<br />
0.10<br />
0.05<br />
0.02<br />
0.01<br />
0.003<br />
0.001<br />
(a) (b)<br />
Probability<br />
−4 −3 −2 −1 0<br />
Data<br />
1 2 3 4<br />
Figure 6. (a) is a histogram <strong>of</strong> normalised data values in t1-noise ridges.<br />
(b) plots the experimental values against an normal probability distribution. The<br />
data values were obtained from an HSQC spectrum <strong>of</strong> sucrose in peak-free ranges<br />
F1 = 157.0 − 97.60 ppm <strong>and</strong> F1 = 55.38 − 3.768 ppm. t1-noise ridges were<br />
identified by F1 traces with an interquartile range <strong>of</strong> less than 5000.<br />
To estimate this distribution, a relatively large number <strong>of</strong> data points were assessed by considering<br />
areas <strong>of</strong> t1-noise ridges free from peaks. However, as indicated by Figure 3, the amplitude <strong>of</strong><br />
the noise varies across a t1-noise ridge, so values are normalised by dividing by the interquartile<br />
range <strong>of</strong> the F1 trace. (As discussed below, this is a relatively robust estimator <strong>for</strong> the noise<br />
amplitude.)<br />
Figure 6 shows the distribution <strong>of</strong> the normalised t1-noise data points from a HSQC spectrum<br />
<strong>of</strong> sucrose. t1-noise ridge sections were identified by taking peak-free subsets <strong>of</strong> F1, <strong>and</strong> F2 values<br />
where the trace interquartile range was significantly above that <strong>of</strong> the thermal noise. The histogram<br />
shows the shape <strong>of</strong> the normal distribution. The normal probability plot <strong>of</strong> the data is also<br />
indicative <strong>of</strong> a normal distribution: the plot is very linear, especially in the central region, although<br />
the curvature at larger negative data values suggests that the left tail <strong>of</strong> the data distribution is<br />
shorter than would be expected. Similar results were obtained <strong>for</strong> the noise distribution in other<br />
HSQC spectra.<br />
2.3.2. Estimators <strong>for</strong> Noise Distribution Parameters. Figure 6 suggests that mean <strong>of</strong> the noise is<br />
approximately zero: a calculation using the same data gives −0.0061. This might be expected<br />
<strong>for</strong> spectra that are accurately baselined (so that signal-free areas <strong>of</strong> the spectrum approach zero<br />
intensity), <strong>and</strong> if, as it appears, the nature <strong>of</strong> the noise causes the intensity to vary above <strong>and</strong><br />
below the actual value <strong>of</strong> the spectrum. The analysis below makes this assumption throughout.<br />
The interquartile range (iqr), is used as an estimator <strong>for</strong> st<strong>and</strong>ard deviation <strong>of</strong> the normal<br />
distribution. This estimator is used as it is more than robust than a direct evaluation <strong>of</strong> the<br />
st<strong>and</strong>ard deviation. If the separated noise spectra included some data points from genuine peaks<br />
in addition to the t1-noise itself, most <strong>of</strong> the large magnitude data points will be outside the<br />
25–75% quartile range measured by the iqr. Although the peak-related data points may skew the<br />
quartile distribution slightly, they will have significantly less impact on the value <strong>of</strong> the iqr than<br />
on the st<strong>and</strong>ard deviation calculation that considers the values <strong>of</strong> all data points, especially if the<br />
peaks are large.<br />
Given this robustness, <strong>and</strong> the relatively small proportion <strong>of</strong> each signal that contains peaks in<br />
the <strong>2D</strong> HSQC spectra used in this project, the iqr estimate is applied to the entire trace, including<br />
the genuine peaks, to give an estimate <strong>for</strong> the noise.<br />
The st<strong>and</strong>ard deviation σ can be calculated from the iqr using the relationship:<br />
σ(·) = QN iqr(·) (2.1)<br />
10
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
The value <strong>of</strong> the constant QN is derived as follows.<br />
Assuming the mean as zero as above, <strong>and</strong> using the definition <strong>of</strong> interquartile range <strong>and</strong> symmetry<br />
<strong>of</strong> the distribution, gives:<br />
q<br />
2<br />
− q<br />
2<br />
fN(x)dx = 1<br />
2<br />
where q is the interquartile range, <strong>and</strong> fN is the probability density function <strong>of</strong> the normal distribution<br />
<strong>of</strong> mean µ <strong>and</strong> st<strong>and</strong>ard deviation σ, i.e.:<br />
Combining (2.2) <strong>and</strong> (2.3) gives:<br />
(by substituting u = x/( √ 2σ))<br />
fN(x) = 1<br />
σ √ 2π e−(x−µ)2 /(2σ 2 )<br />
1 1<br />
=<br />
2<br />
σ √ 2π<br />
= 1<br />
√ π<br />
q<br />
2<br />
− q<br />
2<br />
q<br />
2 √ 2σ<br />
− q<br />
2 √ 2σ<br />
= 2<br />
q<br />
2<br />
√<br />
π<br />
√ 2σ<br />
0<br />
where erf(x) is the error function, defined as,<br />
e −x2 /(2σ 2 ) dx<br />
e −u2<br />
du<br />
e −u2<br />
du<br />
<br />
q<br />
= erf<br />
2 √ <br />
2σ<br />
erf(x) = 2<br />
√ π<br />
Denoting the inverse <strong>of</strong> the error function as erf −1 , then (2.4) gives,<br />
q<br />
σ =<br />
2 √ 2erf −1 ( 1<br />
2 )<br />
<strong>and</strong> thus,<br />
<br />
QN = 2 √ 2 erf −1<br />
−1 1<br />
2<br />
x<br />
0<br />
(2.2)<br />
(2.3)<br />
(2.4)<br />
e −u2<br />
du (2.5)<br />
The value <strong>of</strong> erf −1 (1/2) can be estimated numerically to give QN ≈ 0.7413.<br />
2.3.3. Wavelet Noise Separation. The requirement to separate small amplitude signals from larger<br />
components in consistent with the properties <strong>of</strong> wavelet denoising described in section B.7.1.<br />
The normal distribution <strong>of</strong> the noise suggests that the denoising threshold could be derived<br />
from the st<strong>and</strong>ard deviation <strong>of</strong> the noise signal as the universal threshold (see section B.7.2).<br />
However, this method derives a threshold that <strong>of</strong>ten overestimates the maximum detail coefficient<br />
expected from the noise in a signal <strong>of</strong> given length[1]. If used <strong>for</strong> separating the t1-noise, it is likely,<br />
there<strong>for</strong>e, to include values from genuine peaks <strong>and</strong> there<strong>for</strong>e adversely affect the calculations <strong>of</strong><br />
correlations between t1-noise traces.<br />
Instead, a threshold is derived based on the st<strong>and</strong>ard deviation <strong>of</strong> the coefficients at a given<br />
wavelet decomposition level. The iqr <strong>of</strong> the detail coefficients is used to estimate the st<strong>and</strong>ard<br />
deviation using equation (2.1). 2 A multiple <strong>of</strong> the st<strong>and</strong>ard deviation is then used as the threshold<br />
to give confidence intervals related to the normal distribution. For example, a threshold <strong>of</strong> 3 times<br />
the st<strong>and</strong>ard deviation would be expected to include 99.73% <strong>of</strong> the coefficients resulting from the<br />
noise.<br />
2 Note that the assumption is made here that the detail coefficients exhibit a normal distribution when the<br />
underlying signal has the same distribution.<br />
11<br />
(2.6)<br />
(2.7)
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
If dm,n are the detail coefficients at decomposition level m, then the threshold <strong>for</strong> this level is<br />
given by:<br />
Λm = Kσ ({dm,n})<br />
= KQN iqr({dm,n}) (2.8)<br />
where K is a constant multiplier <strong>of</strong> the st<strong>and</strong>ard deviation to be chosen (e.g. 3 <strong>for</strong> the 99.73%<br />
interval described above), σ(·) the st<strong>and</strong>ard deviation function, <strong>and</strong> iqr(·) the interquartile range<br />
function.<br />
In this context, hard thresholding (see section B.7.2) has the disadvantage that any detail<br />
coefficients just outside the ‘confidence interval’ <strong>for</strong> the noise (defined in terms <strong>of</strong> the st<strong>and</strong>ard<br />
deviation) will be unaffected, <strong>and</strong> so any associated noise signal will be left in the ‘peak’ spectrum<br />
(i.e. the spectrum after denoising) rather than contribute to the t1-noise spectrum.<br />
S<strong>of</strong>t thresholding overcomes this problem, but has the disadvantage that all coefficients are<br />
modified by an amount equal in absolute value to the threshold. This has the effect <strong>of</strong> decreasing<br />
the height—<strong>and</strong> significantly affecting the overall volume—<strong>of</strong> the peak. The peak volume is a key<br />
datum <strong>for</strong> comparing spectra <strong>and</strong>, so, with a view to an algorithm <strong>for</strong> minimising peak noise, a<br />
modified <strong>for</strong>m <strong>of</strong> thresholding is created. It has less affect on peak volume than s<strong>of</strong>t thresholding,<br />
but retains the ability to appropriately include noise just larger than the threshold in the t1-noise<br />
spectrum.<br />
The new method is named here as ‘gradual’ thresholding since it gradually changes from s<strong>of</strong>t<br />
thresholding when the coefficients are close to the threshold to hard thresholding <strong>for</strong> coefficients<br />
larger in absolute value. The definition is:<br />
d S m,n =<br />
0 if |dm,n| < Λm<br />
dm,n<br />
|dm,n|<br />
<br />
|dm,n| − Λm2<br />
|dm,n|<br />
<br />
otherwise<br />
where Λm is the threshold value. By comparison with equation B.69 in appendix B, it can be<br />
seen that this is the s<strong>of</strong>t thresholding method but with the amount by a coefficient is changed now<br />
modified by a factor <strong>of</strong> Λm/|dm,n|.<br />
Although the spectrum is <strong>2D</strong>, the denoising is per<strong>for</strong>med separately on each 1D trace in the F1<br />
direction. Applying wavelet denoising in <strong>2D</strong> would be inappropriate since the thresholding would<br />
assume constant amplitude noise over regions <strong>of</strong> the spectrum with a non-zero F2 width, but, from<br />
above, the t1-noise amplitude varies with F2.<br />
Figure 7 shows the spectra resulting from wavelet denoising using the three thresholding methods.<br />
The denoising was applied separately to each F1 trace in turn. The threshold, at each wavelet<br />
decomposition level, was 3 times the st<strong>and</strong>ard deviation in all cases; the wavelet decomposition<br />
was to 9 levels <strong>and</strong> used the Coiflet wavelet <strong>of</strong> order 2. (The Coiflet wavelet was chosen <strong>for</strong><br />
since it approximately symmetrical, <strong>and</strong>—unlike the Mexican Hat wavelet used earlier—is both<br />
orthogonal <strong>and</strong> compactly supported, enabling its use in the pyramid algorithm.)<br />
The original (noisy) spectrum is that shown in Figure 1. The peak spectrum (a) resulting from<br />
hard threshold shows some remaining large amplitude noise. S<strong>of</strong>t thresholding (b) more accurately<br />
removes most <strong>of</strong> this noise, but does reduce the height <strong>of</strong> the peaks (compare the intense peak<br />
at about F2 = 3.55 ppm in each spectrum). Gradual thresholding (c) still removes most <strong>of</strong> the<br />
noise, but has less effect on peak height. The t1-noise spectrum in (d) shows a small amount <strong>of</strong><br />
the peak signal ‘leaking’ into this spectrum. In general, choosing the thresholding value—in this<br />
case by changing the multiplier K in (2.8)—is a compromise between capturing most <strong>of</strong> the noise<br />
<strong>and</strong> avoiding leakage <strong>of</strong> the peak signal.<br />
Other thresholding methods were also investigated. One promising method leveraged the fact<br />
that noise has both positive <strong>and</strong> negative intensities, but that in a properly phase-corrected spectrum,<br />
genuine peaks have only positive intensities. The largest absolute value <strong>of</strong> negative data<br />
values there<strong>for</strong>e is related only to the noise <strong>and</strong> can be used to derive the threshold. However, this<br />
method is not considered in detail here since it is not extendable to the complex spectra used in<br />
later analysis (see section 2.5).<br />
12<br />
(2.9)
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a) (b)<br />
(c) (d)<br />
Figure 7. Example <strong>of</strong> t1-noise separation using wavelet denoising in an HSQC<br />
spectrum <strong>of</strong> sucrose. (Only a small section <strong>of</strong> the F2 range is shown.) (a),(b)<br />
<strong>and</strong> (c) are the peak spectra resulting from noise separation using hard, s<strong>of</strong>t <strong>and</strong><br />
gradual thresholding methods respectively. (d) shows the corresponding noise<br />
spectrum resulting from the gradual thresholding method, using a different scale<br />
<strong>for</strong> the intensity.<br />
One disadvantage <strong>of</strong> wavelet denoising was found to be the introduction <strong>of</strong> ‘troughs’ close to<br />
peaks, <strong>and</strong> the introduction <strong>of</strong> small artefacts near the base <strong>of</strong> peaks. These observations can can<br />
be characterised as ‘pseudo-Gibbs’ phenomena, similar to the effects seen in Fourier trans<strong>for</strong>ms<br />
<strong>of</strong> rapidly changing signals, <strong>and</strong> poor approximation to the original signal using the modified<br />
coefficients owing to the wavelet shape[20].<br />
The artefacts can be reduced using a non-decimating wavelet decomposition as described in B.8.<br />
The disadvantage is the processing time: if the decomposition is to m levels, this requires 2 m<br />
separate implementations <strong>of</strong> the pyramid algorithm (with a shift in the signal by one unit <strong>for</strong><br />
each) <strong>for</strong> each trace, compared to just one <strong>for</strong> the st<strong>and</strong>ard wavelet decomposition. A compromise<br />
is to per<strong>for</strong>m only a proportion <strong>of</strong> the 2 m shifts[20].<br />
Figure 8 shows examples <strong>of</strong> these modified techniques in the same HSQC spectrum as previously,<br />
but plots the results <strong>for</strong> an F1 trace. The wavelet function <strong>and</strong> threshold are the same as be<strong>for</strong>e.<br />
The troughs <strong>and</strong> artefacts (particularly the large negative ‘peaks’) can be seen in (b). Although<br />
the troughs are largely removed in (c), the smaller scale artefacts remain. A translation invariant<br />
wavelet decomposition in (d) does little to reduce them.<br />
2.3.4. Noise Separation by Direct Signal Thresholding. An alternative method <strong>of</strong> separation is<br />
to simply threshold the spectrum directly without per<strong>for</strong>ming a wavelet decomposition. The<br />
threshold value is calculated in the same way as <strong>for</strong> the wavelet noise separation—as multiple <strong>of</strong><br />
the st<strong>and</strong>ard deviation—but derived from the iqr <strong>of</strong> the spectrum itself rather than <strong>of</strong> the detail<br />
coefficients. The same thresholding methods are still applicable, <strong>and</strong> the advantages <strong>of</strong> using the<br />
gradual thresholding method still hold.<br />
Figure 9 shows the results <strong>of</strong> this method on the same region <strong>of</strong> a HSQC spectrum <strong>of</strong> sucrose that<br />
was used <strong>for</strong> wavelet denoising in Figure 7. Equivalent parameters were used: gradual thresholding<br />
using a threshold value <strong>of</strong> 3 times the noise st<strong>and</strong>ard deviation. The peak spectrum shows few <strong>of</strong><br />
13
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
(c)<br />
(d)<br />
Intensity<br />
Intensity<br />
Intensity<br />
Intensity<br />
2<br />
1<br />
0<br />
−1<br />
−1<br />
x 106<br />
3<br />
x 106<br />
3<br />
2<br />
1<br />
0<br />
2<br />
1<br />
0<br />
−1<br />
−1<br />
x 106<br />
3<br />
x 106<br />
3<br />
2<br />
1<br />
0<br />
140<br />
140<br />
140<br />
140<br />
120<br />
120<br />
120<br />
120<br />
100<br />
100<br />
100<br />
100<br />
80<br />
F 1 ( 13 C) / ppm<br />
80<br />
F 1 ( 13 C) / ppm<br />
80<br />
F 1 ( 13 C) / ppm<br />
80<br />
F 1 ( 13 C) / ppm<br />
Figure 8. Example <strong>of</strong> t1-noise separation using wavelet denoising in an HSQC<br />
spectrum <strong>of</strong> sucrose. The F1 trace at F2 = 3.707 ppm is plotted. (a) is the<br />
original trace. (b) is the peak signal after wavelet denoising using 9 levels <strong>of</strong><br />
wavelet decomposition. (c) uses 5 levels <strong>of</strong> wavelet decomposition. (d) uses a<br />
translation invariant decomposition to 5 levels.<br />
14<br />
60<br />
60<br />
60<br />
60<br />
40<br />
40<br />
40<br />
40<br />
20<br />
20<br />
20<br />
20
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
Figure 9. Example <strong>of</strong> t1-noise separation using direct thresholding <strong>of</strong> the signal<br />
in an HSQC spectrum <strong>of</strong> sucrose. (Only a small section <strong>of</strong> the F2 range is shown.)<br />
(a) is the peak spectrum; (b) is the corresponding t1-noise spectrum.<br />
the artefacts seen with wavelet denoising, <strong>and</strong> the noise spectrum shows little ‘leakage’ from the<br />
peaks.<br />
2.3.5. Conclusion. The noise separation by direct thresholding appears to per<strong>for</strong>m best in this<br />
context, in particularly avoiding the introduction <strong>of</strong> artefacts into the spectrum. The <strong>for</strong>m <strong>of</strong> the<br />
underlying signal—large flat sections with occasional positive-only peaks—appears to be unsuitable<br />
<strong>for</strong> wavelet denoising. Examples given in the literature [1, 23] apply wavelet denoising to<br />
more periodic underlying signals, <strong>for</strong> which the direct thresholding method would be unsuitable.<br />
There<strong>for</strong>e the direct thresholding method is used to separate the noise in subsequent analysis.<br />
2.4. Correlation <strong>of</strong> t1-Noise Traces. Having separated the t1-noise, the correlation between<br />
F1 traces in the noise ridges can be analysed, without the large peak values affecting the results.<br />
If the <strong>2D</strong> spectrum is denoted by the function Φ(f1, f2) where the F1 <strong>and</strong> F2 chemical shifts<br />
take discrete values f1 <strong>and</strong> f2 respectively, then an F1 trace <strong>for</strong> F2 = f2 may be denoted by<br />
Φf2(f1).<br />
The correlation <strong>for</strong> two traces is calculated using the <strong>for</strong>mula:<br />
<br />
<br />
ρ(f2, f ′ 2 ) =<br />
<br />
f1<br />
<br />
Φf2(f1) − Φf2<br />
f1<br />
2<br />
Φf2(f1) − Φf2<br />
<br />
Φf ′ 2 (f1) − Φf ′ 2<br />
f1<br />
Φf ′ 2 (f1) − Φf ′ 2<br />
2<br />
(2.10)<br />
where Φf2 denotes the mean <strong>of</strong> Φf2(f1) over the discrete values f1.<br />
Figure 10 shows the correlation <strong>of</strong> F1 traces <strong>for</strong> the section <strong>of</strong> the t1-noise spectrum separated<br />
from a HSQC spectrum <strong>of</strong> sucrose. The noise spectrum is that shown in Figure 9(b).<br />
It can be seen that the higher-frequency noise maxima line Ah is correlated well with traces at<br />
slightly higher frequency (to the left on the horizontal axes); similarly Al is correlated well with<br />
15
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
(c)<br />
F 2 ( 1 H)<br />
Correlation<br />
Correlation<br />
Bl<br />
Bh<br />
Al<br />
Ax<br />
Ah<br />
1<br />
0.5<br />
0<br />
−0.5<br />
−1<br />
1<br />
0.5<br />
0<br />
−0.5<br />
−1<br />
Ah Ax Al Bh Bl<br />
F 2 ( 1 H)<br />
Ah Ax Al Bh Bl<br />
F 2 ( 1 H)<br />
Ah Ax Al Bh Bl<br />
Figure 10. (a) is a pseudocolour plot <strong>of</strong> correlation <strong>of</strong> F1 traces covering the<br />
range F2 = 3.850 − 3.505 ppm in the t1-noise <strong>of</strong> a HSQC spectrum <strong>of</strong> sucrose.<br />
Strong positive correlations (close to +1) are the lightest shades; strong negative<br />
correlations (close to −1) are darkest; the mid shade <strong>of</strong> grey indicates no correlation.<br />
The labels ‘Ah’ <strong>and</strong> ‘Al’ mark the location <strong>of</strong> the noise maxima lines <strong>for</strong><br />
one t1-noise ridge; ‘Bh’ <strong>and</strong> ‘Bl’ similarly <strong>for</strong> a second ridge. ‘Ax’ is the centre<br />
<strong>of</strong> the first t1-noise ridge. (b) plots the correlation relative to the trace Ah. (c)<br />
plots the correlation relative to the trace Ax.<br />
16<br />
F 2 ( 1 H)
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
traces at slightly lower frequencies. Ah is strongly inversely correlated with Al (ρ is close to −1).<br />
The same pattern holds <strong>for</strong> noise maxima lines <strong>of</strong> the second t1-noise ridge, B.<br />
The correlation with nearby F1 traces suggests a method <strong>of</strong> distinguishing small peaks convoluted<br />
with the noise. By subtracting a well-correlated trace (<strong>and</strong> adjusting <strong>for</strong> different relative<br />
amplitudes) from the trace under consideration, peaks present in the current trace, but not in the<br />
correlated traces, might become more prominent than the remaining noise.<br />
An important observation is that Ah is also strongly correlated with Bh, <strong>and</strong> Al with Bl.<br />
This would significantly benefit the algorithm outlined above. Peaks are likely to extend across<br />
nearby traces in the same t1-noise ridge, <strong>and</strong> so would largely cancel out when two nearby traces<br />
are subtracted. However, peaks are less likely to be present at the same location in traces from<br />
different t1-noise ridges, such as Ah <strong>and</strong> Bh.<br />
However, it is noticeable that traces at the centre <strong>of</strong> a t1-noise ridge are strongly correlated<br />
with very few other traces, either in the same or other t1-noise ridges. For example, Figure 10(c)<br />
shows this to be case <strong>for</strong> the trace Ax; equivalently the pseudocolour plot in (a) shows largely mid<br />
grey shades, indicating ρ close to 0, <strong>for</strong> Ax.<br />
2.5. Complex Correlation <strong>of</strong> t1-Noise Traces. The relatively smooth transition <strong>of</strong> correlation,<br />
<strong>for</strong> example considering changes from Ah through Ax to Al <strong>for</strong> the correlation with the trace Ah,<br />
indicates that the noise is in some way changing its ‘phase’ across F2, from being in phase around<br />
Ah (compared to Ah itself) to a phase difference <strong>of</strong> π near Al. By comparison with the method <strong>of</strong><br />
peak phase correction (section A.6.5), this suggests that additional in<strong>for</strong>mation may be contained<br />
in the ‘imaginary’ frequency values resulting from the imaginary coefficients produced by the first<br />
(along F2) Fourier trans<strong>for</strong>m (the spectra analysed so far having consisted <strong>of</strong> only the real frequency<br />
values). The additional in<strong>for</strong>mation may assist in correlating the noise at the centre <strong>of</strong> t1-noise<br />
ridges, such as Ax described above, which are neither in-phase nor completely out-<strong>of</strong>-phase.<br />
Using the additional imaginary frequency values, each data point along an F1 trace now becomes<br />
a complex value. (There are also additional imaginary coefficients resulting from the second Fourier<br />
trans<strong>for</strong>m, but they are not necessary <strong>for</strong> the analysis here, assuming that phase correction <strong>of</strong> the<br />
<strong>2D</strong> spectrum in the F1 direction takes the same <strong>for</strong>m at all F2 values.)<br />
Be<strong>for</strong>e investigating the correlation using both the real <strong>and</strong> imaginary parts <strong>of</strong> the spectrum,<br />
it is necessary to change the way in which the data is uploaded <strong>for</strong> analysis, to re-analyse the<br />
distribution <strong>of</strong> the noise, <strong>and</strong> to modify the noise separation method.<br />
2.5.1. Data. To access the imaginary components, the post-processing Bruker Topspin data files<br />
were accessed directly, rather than using intermediate text files. The data files used were the<br />
(F2 real; F1 real) <strong>and</strong> (F2 imaginary; F1 real) data files: the first is identical to the real spectra<br />
analysed above; the second is the ‘imaginary’ spectrum. 3 The files were read using a matlab<br />
MEX file written in C ++ to produce two matrices - one <strong>for</strong> each spectrum component. The two<br />
matrices were combined to produce a single matrix with complex values.<br />
2.5.2. Noise Distribution. The distribution <strong>of</strong> the complex values in the noise was investigated<br />
with a view to deriving suitable thresholding parameters <strong>for</strong> noise separation. The procedure<br />
described in section 2.3.1 was repeated to produce a relatively large number <strong>of</strong> data points <strong>for</strong><br />
analysis, this time using the full complex spectrum rather than only the real spectrum. The<br />
distribution <strong>of</strong> the modulus <strong>of</strong> the complex values, i.e. |Φ(f1, f2)| where Φ now represents the<br />
complex spectrum intensity, is analysed.<br />
Denoting the real <strong>and</strong> imaginary parts <strong>of</strong> the spectrum as Φ (ℜ) <strong>and</strong> Φ (ℑ) , then,<br />
|Φ| =<br />
<br />
Φ (ℜ)2 + Φ (ℑ)2<br />
(2.11)<br />
If the imaginary spectrum were to have the same normal distribution as the real spectrum was<br />
found to have in section 2.3.1, <strong>and</strong> if the noise in each is independent <strong>of</strong> the other, then owing to<br />
the relationship in (2.11), the modulus would have a Rayleigh distribution (or, equivalently, a χ<br />
3 As described above, the other data files <strong>for</strong> (F2 real; F1 imaginary) <strong>and</strong> (F2 imaginary; F1 imaginary) are not<br />
required <strong>for</strong> this analysis.<br />
17
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Density<br />
0.7<br />
0.6<br />
0.5<br />
0.4<br />
0.3<br />
0.2<br />
0.1<br />
Normalised Modulus<br />
Rayleigh Fit<br />
Weibull Fit<br />
0<br />
0 0.5 1 1.5 2 2.5<br />
Data<br />
3 3.5 4 4.5<br />
Figure 11. Histogram <strong>of</strong> normalised modulus <strong>of</strong> the complex intensity in t1noise<br />
ridges, with fitted Rayleigh <strong>and</strong> Weibull distributions (using the matlab<br />
distribution fitting tool). The data values were obtained from an HSQC spectrum<br />
<strong>of</strong> sucrose in peak-free ranges F1 = 157.0−97.60 ppm <strong>and</strong> F1 = 55.38−3.768 ppm.<br />
t1-noise ridges were identified by F1 traces with a median magnitude <strong>of</strong> less than<br />
5000/ √ 2.<br />
distribution with two degrees <strong>of</strong> freedom). This distribution has a probability density function <strong>of</strong><br />
the <strong>for</strong>m:<br />
fR(x) = x<br />
s2 e−x2 /2s 2<br />
(2.12)<br />
where s is a scaling factor.<br />
Figure 11 shows the distribution <strong>of</strong> the normalised modulus <strong>of</strong> the complex spectrum. The<br />
modulus was normalised using the median modulus value. The fit <strong>of</strong> a Rayleigh distribution (calculated<br />
using the matlab distribution fitting tool) is good, but the fit to a Weibull distribution—<strong>of</strong><br />
which the Rayleigh distribution is a special case—is better[15]. Although not investigated here, a<br />
possible reason why the fit to the Rayleigh distribution is not as good as expected is that the noise<br />
distributions in the real <strong>and</strong> imaginary part <strong>of</strong> the spectrum are not independent <strong>of</strong> one another.<br />
For simplicity, a Rayleigh distribution is assumed <strong>for</strong> the following. The slight loss <strong>of</strong> accuracy is<br />
not significant, since the use made <strong>of</strong> distribution is to provide only an estimate <strong>of</strong> the thresholding<br />
parameter <strong>for</strong> denoising.<br />
2.5.3. Estimators <strong>for</strong> Noise Distribution Parameters. The interquartile range is no longer suitable<br />
as a robust estimator <strong>for</strong> noise distribution parameter, <strong>and</strong> instead the median <strong>of</strong> the modulus is<br />
used. 4 As be<strong>for</strong>e, the contribution from a small number <strong>of</strong> large peaks will have relatively little<br />
effect on the median modulus.<br />
A constant multiplier, K, <strong>of</strong> the median modulus <strong>for</strong> use as a threshold in noise separation—<br />
equivalent to the same constant in (2.8)—is derived as follows.<br />
4 If the median <strong>of</strong> the absolute value were used <strong>for</strong> the purely real spectrum, the value would be half that <strong>of</strong> the<br />
interquartile range. This factor, combined with the √ 2 increase in the modulus compared to the real part suggested<br />
by equation (2.11), is the reason <strong>for</strong> the adjustment <strong>of</strong> the upper limit <strong>of</strong> the median magnitude in Figure 11 to<br />
5000/ √ 2: the equivalent limit used to identify streaks using iqr in Figure 6 was 5000.<br />
18
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
If the median modulus is denoted by η, then,<br />
η<br />
fR(x)dx = 1<br />
2<br />
by definition <strong>of</strong> the median. Substituting from (2.12),<br />
1<br />
2 =<br />
η<br />
x<br />
s2 e−x2 /2s 2<br />
dx<br />
0<br />
0<br />
<br />
−e −x2 /2s 2η =<br />
0<br />
= 1 − e −η2 /2s 2<br />
0<br />
(2.13)<br />
(2.14)<br />
Thus,<br />
η2 = ln 2 (2.15)<br />
2s2 If the proportion <strong>of</strong> data values within the upper limit Kη is πK, then from (2.12),<br />
Kη<br />
x<br />
πK =<br />
s2 e−x2 /2s 2<br />
dx<br />
<strong>and</strong> so,<br />
=<br />
<br />
−e −x2 /2s 2 Kη<br />
0<br />
= 1 − e −K2 η 2 /2s 2<br />
(2.16)<br />
− K2η2 2s2 = ln (1 − πK) (2.17)<br />
Substituting from (2.15) gives,<br />
K 2 ln (1 − πK)<br />
= − (2.18)<br />
ln 2<br />
hence,<br />
<br />
ln(1 − πK)<br />
K = − (2.19)<br />
ln 2<br />
For the real spectrum with a normal noise distribution, a threshold <strong>of</strong> 3 times the st<strong>and</strong>ard<br />
deviation—or equivalently 2.224 times the iqr using (2.1)—was used to select approximately<br />
99.73% <strong>of</strong> the noise values. For an equivalent proportion assuming a Rayleigh distribution <strong>of</strong><br />
the noise in the complex spectrum, equation (2.19) gives K ≈ 2.921.<br />
2.5.4. Noise Separation <strong>for</strong> the Complex Spectrum. The separation <strong>of</strong> t1-noise in the complex<br />
spectrum is achieved using the equivalent <strong>of</strong> the gradual thresholding <strong>of</strong> the direct signal that<br />
was used <strong>for</strong> the real spectrum. The quantity that is thresholded is the modulus <strong>of</strong> the complex<br />
spectrum, leaving the argument (phase) unchanged. If a trace in the complex spectrum is written<br />
in polar <strong>for</strong>m:<br />
Φf2(f1) = r(f1)e iθ(f1)<br />
(2.20)<br />
where r(f1) is the modulus <strong>and</strong> θ(f1) the argument, then the thresholding is applied to the values<br />
r(f1).<br />
Figure 12 shows the results <strong>of</strong> the denoising <strong>of</strong> the complex spectrum on the same section <strong>of</strong> the<br />
HSQC spectrum as used previously. This can be compared with denoising <strong>of</strong> the real spectrum<br />
shown in Figure 9. Note that since the plots <strong>for</strong> the complex spectrum show the modulus <strong>of</strong> the<br />
complex intensity values, there are no negative values <strong>and</strong> the shape <strong>of</strong> the peaks differ.<br />
Wavelet denoising—thresholding <strong>of</strong> the detail coefficients—was also investigated <strong>for</strong> the complex<br />
spectrum. Rather than using complex wavelets, which do not have compact support[16] <strong>and</strong> are<br />
there<strong>for</strong>e unsuitable <strong>for</strong> the pyramid algorithm decomposition, the real <strong>and</strong> imaginary parts <strong>of</strong> a<br />
trace were decomposed separately using real wavelets. Complex detail coefficients were derived by<br />
combining the corresponding detail coefficients at the same level <strong>and</strong> position, <strong>and</strong> the modulus<br />
<strong>of</strong> the detail coefficient thresholded as described above. The thresholded values were then split<br />
19
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
Figure 12. Example <strong>of</strong> t1-noise separation using direct thresholding <strong>of</strong> the modulus<br />
<strong>of</strong> the complex signal in an HSQC spectrum <strong>of</strong> sucrose. (Only a small section<br />
<strong>of</strong> the F2 range is shown.) (a) is the modulus <strong>of</strong> the complex intensity in the peak<br />
spectrum; (b) is the corresponding plot <strong>for</strong> the t1-noise spectrum.<br />
into real <strong>and</strong> imaginary parts to enable wavelet recomposition <strong>of</strong> the real <strong>and</strong> imaginary peak <strong>and</strong><br />
noise spectra using the inverse pyramid algorithm.<br />
As with the real spectrum, wavelet denoising tended to introduce artefacts. The direct thresholding<br />
<strong>of</strong> the spectrum was there<strong>for</strong>e used in preference.<br />
2.5.5. Complex Correlation. The complex correlation between F1 traces in the complex t1-noise<br />
spectrum is calculated using an extension <strong>of</strong> the <strong>for</strong>mula <strong>for</strong> the (real-valued) correlation (equation<br />
(2.10)):<br />
<br />
<br />
<br />
<br />
Φf2(f1) − Φf2 Φ f1<br />
∗ f ′ (f1) − Φ<br />
2<br />
∗ f ′ 2<br />
2<br />
Φf2(f1) − Φf2<br />
<br />
(2.21)<br />
ρ(f2, f ′ 2 ) =<br />
<br />
Φf f1<br />
f1<br />
′ 2 (f1) − Φf ′ 2<br />
2<br />
where ∗ indicates the complex conjugate. (The same symbol, ρ, was used <strong>for</strong> the st<strong>and</strong>ard correlation,<br />
but will denote the complex correlation in the following.) When considered in polar <strong>for</strong>m, the<br />
complex correlation can be interpreted as follows: the argument indicates the ‘phase difference’<br />
between the two traces, <strong>and</strong> the modulus indicates the degree <strong>of</strong> similarity between the traces<br />
when the two traces are brought into phase. Note that the complex correlation is not symmetrical<br />
in terms <strong>of</strong> f2 <strong>and</strong> f ′ 2: ρ(f2, f ′ 2) = ρ(f ′ 2, f2) ∗ .<br />
Figure 13 is the equivalent <strong>of</strong> Figure 10 but using the complex correlation. The modulus <strong>of</strong><br />
the complex correlation is plotted, ranging from 0 to 1, rather than the actual value used in the<br />
correlation <strong>of</strong> the real spectrum which had the range −1 to +1. (a) <strong>and</strong> (b) show the degree<br />
<strong>of</strong> correlation, irrespective <strong>of</strong> phase. In this case, it can be seen that the complex trace <strong>for</strong> the<br />
‘trough’ Ax at the centre <strong>of</strong> the ridge is now well-correlated with other traces in t1-noise ridge<br />
A, <strong>and</strong> also with traces in ridge B. Compare this with Figure 10 using only the real spectrum,<br />
20
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
where the same trace was poorly correlated. (c) shows that the phase <strong>of</strong> the noise in the complex<br />
spectrum, relative to Ax, changes smoothly across a t1-noise ridge: this can be seen <strong>for</strong> the both<br />
across Ah to Al <strong>and</strong> Bh to Bl. Other spectra showed a similar pattern <strong>of</strong> correlation <strong>and</strong> phase<br />
change.<br />
In peak-free F2 ranges either side <strong>of</strong> a ridge, the argument <strong>of</strong> the complex correlation tends<br />
to stay close to a constant value, <strong>and</strong> the correlation between traces in these regions is strong.<br />
For example, the left-h<strong>and</strong> (higher frequency) end <strong>of</strong> Figure 13(c) shows the start <strong>of</strong> the constant<br />
phase behaviour, <strong>and</strong> the region <strong>of</strong> light shades in the the lower left-h<strong>and</strong> corner <strong>of</strong> (a) show that<br />
the traces are correlated well with one another. The constant arguments (phases) on the higher<br />
<strong>and</strong> lower frequency sides differ by approximately π, i.e. the noise <strong>of</strong> the higher frequency side<br />
is exactly out-<strong>of</strong>-phase with that on the lower frequency side. One observation from this is that<br />
t1-noise must extend some distance either side <strong>of</strong> the main ridge (although at low amplitudes),<br />
to enable this continued correlation: r<strong>and</strong>om noise would show no correlation <strong>and</strong> r<strong>and</strong>om phase<br />
with Ax. This is useful <strong>for</strong> the denoising algorithm since the t1-noise region extends significantly<br />
further than the width <strong>of</strong> a genuine peak. Of course, the presence <strong>of</strong> other t1-noise ridges modifies<br />
this behaviour, <strong>and</strong> the fluctuations in the argument (phase) <strong>of</strong> the correlation to the left <strong>of</strong> Ah,<br />
be<strong>for</strong>e reaching a region <strong>of</strong> more constant values, is indicative <strong>of</strong> weaker t1-noise ridges in this<br />
frequency range.<br />
An alternative representation <strong>of</strong> the change in the complex correlation, particularly the phase,<br />
is shown in Figure 14. The figure considers the complex correlation compared to traces in a<br />
relatively isolated t1-noise ridge to the higher F2 frequency end <strong>of</strong> the HSQC spectrum <strong>of</strong> sucrose;<br />
the t1-noise ridges used in the examples above are convoluted with weaker ridges nearby which<br />
produce a more complex pattern <strong>of</strong> phase changes than this isolated ridge. The figure shows the<br />
correlation with all 2048 traces across the entire F2 range <strong>of</strong> the noise spectrum, plotted on an<br />
Arg<strong>and</strong> diagram. As can be seen in (a), relative to a trace at a frequency slightly higher than<br />
the noise maxima line (a position on the left ‘flank’ <strong>of</strong> the ridge), the majority <strong>of</strong> other traces<br />
tend to be correlated with a phase difference <strong>of</strong> 0 or <strong>of</strong> π, corresponding to be either in phase or<br />
exactly out-<strong>of</strong>-phase. (c) shows that the ‘trough’ in the centre <strong>of</strong> the t1-noise ridge is at a phase<br />
difference <strong>of</strong> ±π/2 with the majority <strong>of</strong> other traces, while (b) shows that the higher frequency<br />
noise maxima line shows a behaviour in between these two.<br />
2.5.6. Discussion - Possible Use in Phase Correction. A phase correction to the <strong>NMR</strong> spectrum<br />
<strong>of</strong> the type described in A.6.5, made across the F2 direction has no effect on the complex corre-<br />
, have the same phase correction applied. However, if the<br />
lation if the two traces, Φf2 <strong>and</strong> Φf ′ 2<br />
phase correction is say, a first- or second-order change in terms <strong>of</strong> F2, rather than a constant, by<br />
consideration <strong>of</strong> equations (A.24) <strong>and</strong> (2.21), it can be seen that the complex correlation modulus<br />
will be unchanged, but the argument will change by an amount equal to the difference in phase<br />
corrections applied to Φf2 <strong>and</strong> Φf ′ 2 .<br />
This suggests a method <strong>of</strong> using the argument <strong>of</strong> the t1-noise complex correlation to calculate<br />
the phase correction required to an uncorrected spectrum. From the observation above, in regions<br />
free <strong>of</strong> peaks, the argument <strong>of</strong> the complex correlation (measured against a chosen, fixed, trace)<br />
is expected to be a constant value, but an unphased spectrum may show the argument phase<br />
changing, say, linearly with F2 instead. In this case, a first-order phase correction could be derived<br />
based on this linear behaviour: essentially the first-order phase correction that would make the<br />
t1-noise correlation argument constant in peak-free regions.<br />
A short investigation <strong>of</strong> this was per<strong>for</strong>med, but found that the correlation argument contains<br />
significant fluctuations even in the peak-free regions making accurate determination <strong>of</strong> the phase<br />
correction difficult. A practical method would require robust isolation <strong>of</strong> the linear (or secondorder<br />
etc.) change in the correlation argument from the noisy fluctuations.<br />
2.5.7. Conclusion. The complex correlation calculated on the full complex spectrum is a better<br />
choice <strong>for</strong> using similarity between F1 traces to identify noise. Owing to the ‘phase change’ in<br />
the t1-noise across a ridge, the central ‘trough’ is poorly correlated with other traces in the real<br />
spectrum, but in the complex spectrum it is well correlated with other traces in the same ridge<br />
<strong>and</strong> in other ridges.<br />
21
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
(c)<br />
F 2 ( 1 H)<br />
Modulus <strong>of</strong><br />
Complex Correlation<br />
Argument <strong>of</strong><br />
Complex Correlation<br />
Bl<br />
Bh<br />
Al<br />
Ax<br />
Ah<br />
1<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
3.142<br />
0<br />
−3.142<br />
Ah Ax Al Bh Bl<br />
F 2 ( 1 H)<br />
Ah Ax Al Bh Bl<br />
F 2 ( 1 H)<br />
Ah Ax Al Bh Bl<br />
Figure 13. (a) is a pseudocolour plot <strong>of</strong> modulus <strong>of</strong> the complex correlation <strong>of</strong><br />
F1 traces covering the range F2 = 3.850 − 3.505 ppm in the t1-noise <strong>of</strong> a HSQC<br />
spectrum <strong>of</strong> sucrose. Strong correlations (close to 1) are the lightest shades; weak<br />
correlations (close to 0) are darkest. The labels ‘Ah’ <strong>and</strong> ‘Al’ mark the location <strong>of</strong><br />
the noise maxima lines <strong>for</strong> one t1-noise ridge; ‘Bh’ <strong>and</strong> ‘Bl’ similarly <strong>for</strong> a second<br />
ridge. ‘Ax’ is the centre <strong>of</strong> the first t1-noise ridge. (b) <strong>and</strong> (c) plot the modulus<br />
<strong>and</strong> argument, respectively, <strong>of</strong> the complex correlation relative to the trace Ax.<br />
22<br />
F 2 ( 1 H)
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
(c)<br />
Imaginary Part <strong>of</strong><br />
Complex Correlation<br />
Imaginary Part <strong>of</strong><br />
Complex Correlation<br />
Imaginary Part <strong>of</strong><br />
Complex Correlation<br />
1<br />
0.5<br />
0<br />
−0.5<br />
−1<br />
−1 −0.5 0 0.5 1<br />
1<br />
0.5<br />
0<br />
−0.5<br />
Real Part <strong>of</strong> Complex Correlation<br />
−1<br />
−1 −0.5 0 0.5 1<br />
1<br />
0.5<br />
0<br />
−0.5<br />
Real Part <strong>of</strong> Complex Correlation<br />
−1<br />
−1 −0.5 0 0.5 1<br />
Real Part <strong>of</strong> Complex Correlation<br />
Figure 14. Plots <strong>of</strong> the noise complex correlation represented on an Arg<strong>and</strong><br />
diagram relative to trace <strong>of</strong> a t1-noise ridge in an HSQC spectrum <strong>of</strong> sucrose. (a)<br />
shows the complex correlation relative to a trace at a slightly higher frequency<br />
(F2 = 5.315 ppm) than an ‘h’ noise maxima line (i.e. on the left ‘flank’ <strong>of</strong> the<br />
t1-noise ridge). (b) <strong>and</strong> (c) shows the complex correlation relative to a higher<br />
frequency (‘h’) noise maxima line (F2 = 5.302 ppm) <strong>and</strong> the ‘trough’ in the<br />
centre <strong>of</strong> a t1-noise ridge (F2 = 5.289 ppm), respectively.<br />
23
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
2.6. <strong>Denoising</strong> Algorithm. The denoising algorithm makes use <strong>of</strong> the correlation between traces<br />
in the complex spectrum to distinguish between t1-noise <strong>and</strong> ‘genuine’ peaks. It makes the assumption<br />
that a genuine peak will be present in a small number <strong>of</strong> nearby F1 traces, but that the<br />
noise signal is very similar in traces separated by distances larger than the peak width. 5<br />
2.6.1. Algorithm Description.<br />
(1) The complex spectrum is separated into the peak <strong>and</strong> noise components, denoted Φ (p) (f1, f2),<br />
<strong>and</strong> Φ (n) (f1, f2), by gradual thresholding <strong>of</strong> the spectrum as described above.<br />
(2) For each discrete value <strong>of</strong> f2, the complex correlation <strong>of</strong> the noise trace Φ (n)<br />
with all other<br />
f2<br />
traces Φ (n)<br />
f ′ (f<br />
2<br />
′ 2 = f2) is calculated using (2.21). The complex correlation is considered in<br />
polar <strong>for</strong>m, i.e.<br />
ρ(f2, f ′ 2) = rf2(f ′ 2)e iθf (f 2 ′<br />
2 )<br />
(2.22)<br />
(3) For the f2 trace under consideration, a set, M, <strong>of</strong> f ′ 2 values is chosen according to the<br />
criteria:<br />
Highly Correlated: The set contains only values <strong>for</strong> which the correlation is above a<br />
threshold, that is: r(f ′ 2 ) ≥ R (M)<br />
Best Correlated: The set contains (at most) the N (M) best correlated values, i.e <strong>for</strong><br />
which the values r(f ′ 2 ) are the largest.<br />
Distant: f ′ 2 is outside the range [f2 − F (M), f2 + F (M)] where F (M) > 0 is a chosen<br />
constant.<br />
Phase Balanced: The set contains an equal number <strong>of</strong> values <strong>for</strong> which |θf2(f ′ 2 )| < π/2<br />
<strong>and</strong> |θf2(f ′ 2)| ≥ π/2.<br />
The purpose <strong>of</strong> these criteria is discussed below.<br />
(4) Using the set M, an unnormalised masking trace is derived as:<br />
Φ (m′ )<br />
f2 (f1) = <br />
f ′ 2 ∈M<br />
<br />
The denominator, median<br />
w [rf2(f ′ 2 )]<br />
<br />
Φ (n)<br />
f ′ (f1)<br />
2<br />
median(|Φ (n)<br />
f ′ 2<br />
|) e−iθf 2 (f ′<br />
2 )<br />
(2.23)<br />
|Φ (n)<br />
f ′ | , robustly normalises each trace, as discussed above,<br />
2<br />
be<strong>for</strong>e contribution to the mask. The factor e−iθf (f 2 ′ 2 ) adjusts the ‘phase’ <strong>of</strong> each f ′ 2 trace<br />
to that <strong>of</strong> f2.<br />
w(·) is a weighting function that scales the contribution <strong>of</strong> a trace to the mask depending<br />
on the correlation. The weighting function was chosen to be the modulus <strong>of</strong> the correlation<br />
itself, so the expression simplifies to:<br />
Φ (m′ )<br />
f2 (f1) = <br />
f ′ 2 ∈M<br />
Φ (n)<br />
f ′ (f1)<br />
2<br />
median(|Φ (n)<br />
f ′ |)<br />
2<br />
ρ(f2, f ′ 2 )∗<br />
(2.24)<br />
where ∗ indicates the complex conjugate.<br />
(5) The mask is then adjusted so that its median modulus (a measure <strong>of</strong> its signal amplitude)<br />
is the same as that <strong>of</strong> the trace Φ (n)<br />
f2 :<br />
Φ (m)<br />
f2 (f1) = median(|Φ(n) f2 |)<br />
median(|Φ (m′ )<br />
|) f2 Φ(m′ )<br />
(f1) (2.25)<br />
f2<br />
(6) The adjusted masks over all f2 values together <strong>for</strong>m a masking spectrum Φ (m) (f1, f2).<br />
The denoised complex spectrum is constructed by subtracting the mask from the noise<br />
spectrum, <strong>and</strong> adding it back to the peak spectrum:<br />
Φ (d) = Φ (p) + Φ (n) − Φ (m)<br />
5 A quantitative assessment <strong>of</strong> peak width is discussed in section 3.2.<br />
24<br />
(2.26)
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
the superscript (d) indicating the denoised spectrum. The denoised real spectrum (corresponding<br />
to the absorption signal, see A.6) that is used <strong>for</strong> the remaining analysis is<br />
simply the real part <strong>of</strong> Φ (d) .<br />
Note that the algorithm does not test whether the trace at a particular F2 frequency is part <strong>of</strong><br />
a t1-noise ridge. This was based on the observation that the t1-noise continues either side <strong>of</strong> the<br />
visible ridge <strong>for</strong> some distance, albeit at a lower amplitude, <strong>and</strong> continues to show good correlation<br />
with other traces. There<strong>for</strong>e the algorithm attempts to denoise across the entire F2 range.<br />
2.6.2. Masking Criteria.<br />
Highly Correlated: This criterion is straight<strong>for</strong>ward. By picking only highly correlated<br />
traces, the intention is that the mask is very similar to the trace in question <strong>and</strong> so when<br />
the mask is subtracted from the noise, any remaining noise signal has low amplitude.<br />
Best Correlated: This criterion is intended to improve the denoising <strong>of</strong> traces with many<br />
well-correlated traces. By picking only the best correlated, the remaining signal when the<br />
mask is subtracted has the lowest amplitude. Rather than using the single best correlated<br />
trace, the mask is built from a number <strong>of</strong> traces so that if any <strong>of</strong> the traces should have a<br />
small ‘genuine’ peak in it, the effect <strong>of</strong> this peak is minimised.<br />
Distant: The ‘Distant’ criterion avoids the removal <strong>of</strong> small ‘genuine’ peaks: the objective<br />
<strong>of</strong> the algorithm is to minimise the noise but retain any small peaks convoluted with it. A<br />
trace is typically best correlated with it immediate neighbours. Each <strong>of</strong> these neighbours<br />
would contain the peak signal, <strong>and</strong> so without the distant criterion, the mask would also<br />
include the peak signal. When subtracted from the noise spectrum, the mask would remove<br />
the peak (or significantly reduce its intensity). The ‘Distant’ criterion there<strong>for</strong>e avoids the<br />
use <strong>of</strong> near neighbours in deriving the mask.<br />
Phase Balanced: The ‘Phase Balanced’ criterion was introduced when it was found that<br />
small ‘genuine’ peaks in the spectra <strong>of</strong> metabolomic samples were occasionally removed<br />
by the algorithm in particular circumstances. If the trace in question has a peak at a<br />
particular F1 frequency, <strong>and</strong> a number <strong>of</strong> other ridges have a peak at the same frequency,<br />
then many <strong>of</strong> the traces contributing to the mask might contain a peak signal at this<br />
frequency. (The other ridges are too far away from the trace in question <strong>for</strong> the ‘Distant’<br />
criterion to operate.) When the mask derived from these traces is subtracted from the<br />
noise, the peak is reduced or removed.<br />
By reference to Figure 14(a), it can be seen that <strong>for</strong> many traces, their well-correlated<br />
traces are either in phase or out-<strong>of</strong>-phase by a factor <strong>of</strong> π. The effect <strong>of</strong> phase-balancing is<br />
to pick an equal number <strong>of</strong> traces that are in-phase <strong>and</strong> (almost) exactly out-<strong>of</strong>-phase to<br />
<strong>for</strong>m the mask. Since each trace is phase-adjusted by this phase difference when <strong>for</strong>ming<br />
the mask (see equation (2.23)), this means that approximately half the traces are multiplied<br />
by a phase adjustment factor close to −1. If many <strong>of</strong> the traces contributing to the<br />
mask contain peaks, the multiplication <strong>of</strong> about half the traces by −1 can result in the<br />
cancellation <strong>of</strong> peak signal when the mask is <strong>for</strong>med, resulting in less reduction to genuine<br />
peaks in the denoised spectrum. This effect is only partial, being dependent on the exact<br />
choice <strong>of</strong> the traces to <strong>for</strong>m the mask <strong>and</strong> the similarity <strong>of</strong> peak signals in these traces.<br />
In addition, the criterion works less well <strong>for</strong> traces where the correlation phase pattern<br />
is more complex. Nevertheless, tests show that this criterion does limit the reduction <strong>of</strong><br />
peak intensity in these particular circumstances.<br />
Figure 15 illustrates phase-balancing using a hypothetical small ‘genuine’ peak convoluted<br />
with the ridge A. When the mask <strong>for</strong> trace Bh is constructed, Ah <strong>and</strong> Al are<br />
a possible pair <strong>of</strong> phase-balanced contributors. The contribution to the real part <strong>of</strong> the<br />
mask from the peak in (b) is shown in (c) where the signal has been phase adjusted by<br />
the phase <strong>of</strong> the complex correlation relative to trace Bh. The contributions from Ah <strong>and</strong><br />
Al cancel one another, so the peak signal does not appear in the real part <strong>of</strong> the mask.<br />
Since it is the real part <strong>of</strong> the spectrum that will be used <strong>for</strong> analysis after denoising, this<br />
means that the t1-noise at Bh will be removed, correctly, by the noise signals at Ah <strong>and</strong> Al<br />
25
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
(c)<br />
Argument <strong>of</strong><br />
Complex Correlation<br />
Peak Intensity<br />
(Real Component)<br />
Peak Intensity<br />
(Real Component)<br />
3.142<br />
0<br />
−3.142<br />
0<br />
0<br />
Ah Ax Bh<br />
F 2 ( 1 H)<br />
Ah Ax Bh<br />
F 2 ( 1 H)<br />
Ah Ax Bh<br />
Figure 15. An illustration <strong>of</strong> the ‘Phase Balanced’ criterion. (a) shows the phase<br />
angle <strong>of</strong> the complex correlation <strong>of</strong> the t1-noise relative to Bh. (b) is a small<br />
hypothetical peak convoluted with the t1-noise ridge A. (c) is the real component<br />
<strong>of</strong> the contribution to the mask from the peak in (b) after adjustment by the<br />
phase <strong>of</strong> the noise relative to Bh. If Ah <strong>and</strong> Al are a phase-balanced pair chosen<br />
<strong>for</strong> the mask, the contribution from each to the real spectrum mask cancel one<br />
another.<br />
F 2 ( 1 H)<br />
(which are ‘amplified’ by the phase adjustment by bringing the phase <strong>of</strong> the noise signals<br />
into alignment) <strong>and</strong> not by the peak signal (which is cancelled out by the adjustment).<br />
2.6.3. Choice <strong>of</strong> <strong>Denoising</strong> Parameters. All the criteria, <strong>and</strong> the parameters used to control them,<br />
are a balance between removing as much t1-noise as possible while retaining the intensity <strong>of</strong> small<br />
‘genuine’ peaks embedded in the noise. For example, a small ‘distant’ parameter, F (M), results<br />
in better noise reduction but can lead to a reduction in peak intensity. Similarly, the ‘Phase<br />
Balanced’ criterion prevents the reduction <strong>of</strong> small peaks in some circumstances, but <strong>for</strong> traces<br />
with few well-correlated traces, which tends to be the case <strong>for</strong> the ‘troughs’ at the centre <strong>of</strong> t1-noise<br />
ridges, the balancing requirement limits the number <strong>of</strong> traces included in the mask, <strong>of</strong>ten resulting<br />
in poorer noise reduction.<br />
The appropriate parameter values were chosen by experimentation. Note that some are dependent<br />
on the settings <strong>of</strong> the <strong>NMR</strong> experiment itself: <strong>for</strong> example, the ‘distant’ parameter, F (M), is<br />
dependent on the width <strong>of</strong> peaks in the spectrum. The derivation <strong>of</strong> these parameters is discussed<br />
further in section 4. Table 1 shows the typical parameter settings <strong>for</strong> the spectra considered in<br />
this project.<br />
2.7. Results <strong>and</strong> Discussion. To assess the efficacy <strong>of</strong> the denoising algorithm, a series <strong>of</strong><br />
samples were created from solutions <strong>of</strong> sucrose <strong>and</strong> glycine. The HSQC spectrum <strong>of</strong> glycine<br />
26
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Parameter Value<br />
minimum correlation modulus, R (M)<br />
0.5<br />
maximum number <strong>of</strong> traces, N (M) 3 × data points in F2 peak width<br />
minimum distance from trace, F (M) 1 × F2 peak width<br />
phase-balanced yes<br />
Table 1. Typical parameters used <strong>for</strong> deriving the mask spectrum in the denoising<br />
algorithm.<br />
Intensity<br />
−1<br />
−2<br />
−3<br />
x 104<br />
3<br />
2<br />
1<br />
0<br />
140<br />
120<br />
100<br />
80<br />
F 1 ( 13 C) / ppm<br />
Figure 16. F1 trace in the noise component <strong>of</strong> the HSQC spectrum <strong>of</strong> a mixture<br />
<strong>of</strong> sucrose (250 mM) <strong>and</strong> glycine (4 mM), at the centre F2 frequency <strong>of</strong> the<br />
glycine peak. Some <strong>of</strong> the signal <strong>of</strong> the small glycine peak at (F1 = 41.30 ppm,<br />
F2 = 3.434 ppm) can be seen in the trace.<br />
contains a single intense peak at (F1 = 41.30 ppm, F2 = 3.434 ppm) which coincides with a<br />
t1-noise streak in the sucrose spectrum.<br />
The samples were created using a constant concentration <strong>of</strong> sucrose at 250 mM but varying<br />
the glycine concentration to change peak size. The sample considered initially used a glycine<br />
concentration <strong>of</strong> 4 mM, resulting in a peak size a little above the amplitude <strong>of</strong> the t1-noise. Owing<br />
to the small size <strong>of</strong> the peak, when the noise spectrum is separated, a significant portion <strong>of</strong> peak is<br />
included in the noise spectrum as can be seen in Figure 16. The maximum intensity <strong>of</strong> the peak in<br />
the noise spectrum is 2.301 × 10 4 compared to 4.142 × 10 4 in the full spectrum prior to denoising.<br />
The denoising algorithm was per<strong>for</strong>med on this spectrum using the parameters specified in<br />
Table 1. Figure 17 shows the spectra <strong>for</strong> the sample be<strong>for</strong>e <strong>and</strong> after denoising. The reduction in<br />
the t1-noise can be clearly seen.<br />
Figure 18(a) shows the interquartile range be<strong>for</strong>e <strong>and</strong> after denoising across a range <strong>of</strong> the<br />
spectrum that includes all the prominent peaks. It can be seen that iqr is reduced at most F2<br />
values across t1-noise ridges, indicating a reduction in noise. This behaviour is confirmed by<br />
Figure 18(b) which shows the factor by which the iqr is reduced after denoising. Significant<br />
features seen here, <strong>and</strong> also when denoising <strong>of</strong> other HSQC spectra, are that the algorithm is<br />
particularly good at removing noise on the ‘flanks’ <strong>of</strong> t1-noise ridges, even some distance from the<br />
main ridge, but is <strong>of</strong>ten less good near the centre <strong>of</strong> the ridge, <strong>and</strong> particularly the ‘trough’ at the<br />
centre.<br />
The RMS Signal-to-Noise Ratio (SNR) defined in (2.28) is used as a quantitative measure <strong>of</strong><br />
sensitivity, <strong>and</strong> thereby the noise, in the following analysis. Since the t1-noise changes with F2,<br />
an assumption will be made that the noise <strong>of</strong> the F1 trace through the centre <strong>of</strong> peak itself is<br />
representative. So if the peak is at (f1, f2),<br />
SNR = Φ(f1, f2)<br />
σ {Φf2(f1)}<br />
27<br />
60<br />
40<br />
20<br />
(2.27)
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
Figure 17. The HSQC spectrum <strong>of</strong> a mixture <strong>of</strong> sucrose (250 mM) <strong>and</strong> glycine (4<br />
mM) (a) be<strong>for</strong>e <strong>and</strong> (b) after denoising. The F2 range encompasses the majority<br />
<strong>of</strong> prominent peaks.<br />
where Φf2(f1) is the F1 trace through the peak. If a normal distribution <strong>of</strong> the noise in the<br />
real spectrum continues to be assumed, the relationship between the st<strong>and</strong>ard deviation <strong>and</strong> the<br />
interquartile range in (2.1) gives,<br />
Φ(f1, f2)<br />
SNR =<br />
QN iqr {Φf2(f1)}<br />
(2.28)<br />
where QN ≈ 0.7413 from (2.7).<br />
Figure 19 shows the change in noise around the glycine peak as a result <strong>of</strong> denoising. In this<br />
case, the denoising algorithm has not reduced the intensity <strong>of</strong> the peak. (In fact, its maximum<br />
intensity has increased slightly from 4.142 to 4.344 × 10 4 .)<br />
28
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
iqr(Intensity)<br />
Reduction in iqr<br />
x 104<br />
12<br />
10<br />
8<br />
6<br />
4<br />
2<br />
0<br />
5.5<br />
4.5<br />
4<br />
3.5<br />
3<br />
2.5<br />
2<br />
1.5<br />
1<br />
0.5<br />
5.5<br />
Original Spectrum<br />
Denoised Spectrum<br />
5<br />
5<br />
4.5<br />
4.5<br />
4<br />
F 2 ( 1 H) / ppm<br />
4<br />
F 2 ( 1 H) / ppm<br />
Figure 18. (a) plots the interquartile range (a measure <strong>of</strong> noise) in the HSQC<br />
spectrum <strong>of</strong> a mixture <strong>of</strong> sucrose (250 mM) <strong>and</strong> glycine (4 mM) be<strong>for</strong>e <strong>and</strong> after<br />
denoising. The F2 range encompasses all <strong>of</strong> the prominent peaks. (b) plots the<br />
factor by which the interquartile range is reduced after denoising.<br />
The SNR values <strong>for</strong> the glycine peak, calculated using the <strong>for</strong>mula (2.28) are 5.084 be<strong>for</strong>e<br />
denoising <strong>and</strong> 14.34 after, an improvement by a factor <strong>of</strong> 2.82. (Most <strong>of</strong> the improvement is due<br />
to the decrease in the t1-noise rather than the slight increase in the peak intensity.)<br />
2.7.1. Alternative Algorithm. An alternative algorithm considered was to apply the masking algorithm<br />
separately to each level <strong>of</strong> wavelet decomposition <strong>of</strong> the noise trace.<br />
Using the equation (B.64), the pyramid algorithm can be used to deconstruct each noise trace<br />
as:<br />
Φ (n)<br />
f2 (f1) = s (n)<br />
f2;M,0 φM,0(f1) +<br />
M<br />
m=1<br />
2 M−m −1<br />
n=0<br />
3.5<br />
3.5<br />
3<br />
3<br />
d (n)<br />
f2;m,n ψm,n(f1) (2.29)<br />
where φm,n <strong>and</strong> ψm,n are the dilated <strong>and</strong> translated scaling <strong>and</strong> wavelet functions, <strong>and</strong> s (n)<br />
f2;m,n <strong>and</strong><br />
d (n)<br />
f2;m,n<br />
are the approximation <strong>and</strong> detail coefficients. Note that the signal Φ(n)<br />
f2 is complex <strong>and</strong><br />
so the coefficients take complex values, <strong>for</strong>med by using the pyramid algorithm to decompose the<br />
real <strong>and</strong> imaginary parts <strong>of</strong> the noise spectrum separately, <strong>and</strong> then combining the corresponding<br />
coefficients to give complex coefficients. The scaling <strong>and</strong> wavelet functions remain real-valued.<br />
29
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
Intensity<br />
Intensity<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
−1<br />
−2<br />
−3<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
−1<br />
−2<br />
−3<br />
x 10 4<br />
30<br />
x 10 4<br />
30<br />
35<br />
35<br />
40<br />
F 1 ( 13 C) / ppm<br />
40<br />
F 1 ( 13 C) / ppm<br />
45<br />
45<br />
50<br />
50<br />
3.4<br />
3.42<br />
3.44<br />
3.46<br />
3.48<br />
F 2 ( 1 H) / ppm<br />
3.4<br />
3.42<br />
3.44<br />
3.46<br />
3.48<br />
F 2 ( 1 H) / ppm<br />
Figure 19. A section <strong>of</strong> the HSQC spectrum <strong>of</strong> a mixture <strong>of</strong> sucrose (250 mM)<br />
<strong>and</strong> glycine (4 mM) around the glycine peak. (a) shows the section be<strong>for</strong>e denoising<br />
<strong>and</strong>, (b), after.<br />
After decomposing all the F1 noise traces in this way, a mask is found <strong>for</strong> each f2 value in<br />
turn as in the st<strong>and</strong>ard algorithm. However a mask is derived <strong>for</strong> each wavelet decomposition<br />
separately. At each level, m ′ the set <strong>of</strong> detail coefficients d (n)<br />
f2;m ′ ,n is treated as a complex signal<br />
(in terms <strong>of</strong> n), <strong>and</strong> its complex correlation with the equivalent set <strong>of</strong> coefficients <strong>for</strong> all other f2<br />
values is calculated.<br />
30<br />
3.38<br />
3.38
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
iqr(Intensity)<br />
x 104<br />
4.5<br />
4<br />
3.5<br />
3<br />
2.5<br />
2<br />
1.5<br />
1<br />
0.5<br />
0<br />
5.5<br />
St<strong>and</strong>ard <strong>Denoising</strong> Algorithm<br />
Wavelet−Level <strong>Denoising</strong> Algorithm<br />
5<br />
4.5<br />
4<br />
F 2 ( 1 H) / ppm<br />
Figure 20. The interquartile range (a measure <strong>of</strong> noise) in the HSQC spectrum<br />
<strong>of</strong> a mixture <strong>of</strong> sucrose (250 mM) <strong>and</strong> glycine (4 mM) after using the st<strong>and</strong>ard <strong>and</strong><br />
wavelet-level denoising algorithms. The F2 range encompasses all <strong>of</strong> the prominent<br />
peaks.<br />
A masking set <strong>of</strong> detail coefficient, d (n)<br />
f2;m ′ ,n , is then derived using steps 3 to 5 in the st<strong>and</strong>ard<br />
algorithm. This is repeated <strong>for</strong> each level m ′ . From these masking detail coefficients at all levels,<br />
a masking trace is reconstructed using the equivalent <strong>of</strong> equation (2.29), <strong>and</strong> these traces together<br />
<strong>for</strong>m the masking spectrum.<br />
The rationale <strong>for</strong> this approach is that the correlation between traces may change when considering<br />
signal components at different scales (or equivalently at different frequencies), <strong>and</strong> there<strong>for</strong>e<br />
deriving a separate mask at wavelet decomposition level might result in more accurate masking <strong>of</strong><br />
the t1-noise.<br />
This alternative derivation <strong>of</strong> the masking spectrum produces a reduction in t1-noise that is<br />
equivalent, but occasionally slightly worse, than st<strong>and</strong>ard algorithm described above. Figure 20<br />
compares the interquartile range in the denoised spectrum <strong>for</strong> the two algorithms. The waveletlevel<br />
algorithm used the Coiflet wavelet <strong>of</strong> order 2, to 10 levels <strong>of</strong> decomposition. Although the<br />
wavelet-level algorithm is better at reducing noise at low amplitudes, the st<strong>and</strong>ard algorithm<br />
is slightly better at reducing the large amplitude noise towards the centre <strong>of</strong> some <strong>of</strong> the t1noise<br />
ridges. As a—not necessarily representative—indication, the SNR <strong>for</strong> the glycine peak<br />
after the wavelet-level algorithm is slightly lower at 12.57 compared to 14.34 <strong>for</strong> the st<strong>and</strong>ard<br />
algorithm (again, the majority <strong>of</strong> this improvement resulting from the reduction noise rather<br />
than a slight increase in peak intensity). When compared on other spectra, it was found that<br />
the st<strong>and</strong>ard algorithm was more robust, with the wavelet-level algorithm occasionally producing<br />
results significantly worse than the st<strong>and</strong>ard algorithm at a few individual F2 values.<br />
Given its equivalent (or slightly better per<strong>for</strong>mance) in noise reduction, <strong>and</strong> its shorter running<br />
time compared to the the wavelet-level denoising algorithm, the st<strong>and</strong>ard algorithm is used <strong>for</strong><br />
denoising in the subsequent sections <strong>of</strong> this project.<br />
2.8. Comparison to Other t1-Noise Reduction Techniques.<br />
Reference Deconvolution: Another method <strong>of</strong> t1-noise reduction is to use reference deconvolution<br />
as described in [13]. The technique also leverages the correlation between<br />
t1-noise ridges, but works in the time- rather than frequency-domain. The strong t1-noise<br />
ridge associated with the compound used to produce the reference frequency in the sample<br />
is identified, <strong>and</strong> then a (complex spectrum) trace through the ridge is converted back into<br />
31<br />
3.5<br />
3
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
the time-domain by per<strong>for</strong>ming an inverse Fourier trans<strong>for</strong>m in the F1 direction. Comparison<br />
<strong>of</strong> this experimental time-domain signal with a predicted theoretical <strong>for</strong>m enables the<br />
identification <strong>of</strong> a complex correcting function (the equivalent <strong>of</strong> the masking spectrum)<br />
which can then be applied to the entire spectrum. By using a series <strong>of</strong> traces through<br />
the t1-noise ridge <strong>of</strong> the reference signal across a small range <strong>of</strong> F2 values, the technique<br />
can also account <strong>for</strong> changes in the t1-noise in the t2 direction, corresponding to changes<br />
during acquisition <strong>of</strong> the FID.<br />
The reference deconvolution technique is similar to the denoising algorithm described<br />
earlier, essentially using the same correlation properties but applying a masking spectrum<br />
(or correcting function) in the time rather than frequency domain. However, it does require<br />
both a strong reference signal to be identified, <strong>and</strong> <strong>for</strong> the theoretical <strong>for</strong>m <strong>of</strong> that signal<br />
to be calculated (in particular, requiring that the reference signal is not convoluted with<br />
other signals). The denoising algorithm <strong>of</strong> section 2.6 has a desirable property that, by<br />
picking the other traces that each trace is correlated with individually, it can h<strong>and</strong>le the<br />
gradual change in t1-noise with F2 that is observed in the spectra; it is unclear whether<br />
reference deconvolution is adaptable in this manner.<br />
Cadzow Procedure: A further technique is to use the Cadzow procedure to directly denoise<br />
the FIDs as described by [4]. The technique makes use <strong>of</strong> properties <strong>of</strong> a Toeplitz<br />
matrix derived from the FIDs to remove all signals apart from those resulting from N<br />
resonance frequencies. However, the technique requires a priori knowledge <strong>of</strong> the number<br />
<strong>of</strong> resonance frequencies (i.e. the number <strong>of</strong> peaks) in the signal. It there<strong>for</strong>e appears unsuitable<br />
<strong>for</strong> metabolomic pr<strong>of</strong>iling where the number <strong>and</strong> location <strong>of</strong> peaks in the spectrum<br />
is not known in advance.<br />
32
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
3. Automated Peak Picking Using a Genetic Algorithm<br />
Peak Picking is the process <strong>of</strong> identifying the position <strong>of</strong> peaks in an <strong>NMR</strong> spectra, in particular<br />
distinguishing peaks from noise artefacts. Although <strong>NMR</strong> processing s<strong>of</strong>tware provides tools to<br />
assist in peak picking, accurate picking <strong>of</strong>ten requires the experience <strong>of</strong> the experimenter. This<br />
manual process can be time-consuming, especially <strong>for</strong> the spectra <strong>of</strong> metabolomic samples, <strong>and</strong><br />
can be subjective.<br />
This section describes the use a genetic algorithm (GA) (appendix C) to automate peak picking.<br />
The aim is to incorporate some <strong>of</strong> the knowledge used by the experimenter into the algorithm,<br />
<strong>and</strong> to leverage the analysis <strong>of</strong> t1-noise in section 2 to assist in distinguishing small peaks from<br />
noise.<br />
3.1. Peak Shape. The GA attempts to fit experimental peaks to theoretical peak shapes.<br />
In theory, the resonance frequency <strong>of</strong> a nucleus is very well-defined. In practice, the transverse<br />
relaxation process (section A.3.2) leads to line broadening[14] owing to the exponential decay in<br />
the FID <strong>and</strong> its effect on the subsequent Fourier trans<strong>for</strong>m. The theoretical shape is a Lorentzian<br />
peak <strong>of</strong> the <strong>for</strong>m[9]:<br />
w0.5 2 Φ(fc)<br />
Φ(f) =<br />
w0.5 2 + 4(f − fc) 2<br />
where fc the centre frequency <strong>of</strong> the peak, Φ(fc) is the intensity at the centre frequency, <strong>and</strong> w0.5<br />
is the peak width at half-height. In practice, a number <strong>of</strong> experimental <strong>and</strong> instrumental factors<br />
lead to further significant broadening <strong>of</strong> the peak [9, 14].<br />
The shape <strong>of</strong> the peak is also affected by the choice <strong>of</strong> the window function applied to the<br />
FID prior to the Fourier Trans<strong>for</strong>m (section A.6.3). The window function can be used to improve<br />
the sensitivity <strong>of</strong> the experiment, but also affects the peak shape. Peak broadening decreases the<br />
resolution—the ability <strong>of</strong> the experiment to distinguish nearby peaks—<strong>and</strong> the choice <strong>of</strong> window<br />
function is <strong>of</strong>ten a compromise between improved SNR <strong>and</strong> decreased resolution[9].<br />
An analysis <strong>of</strong> peaks in the <strong>2D</strong> HSQC spectra used in this project shows that, as a result <strong>of</strong> the<br />
pre-Fourier Trans<strong>for</strong>m processing, the peak shape is very close to a Gaussian. Figure 21 shows the<br />
examples <strong>of</strong> fitting Lorentzian <strong>and</strong> Gaussian shapes to experiment glycine peaks from samples <strong>of</strong><br />
two different concentration. As can be seen, the fit is good <strong>for</strong> the Gaussian in both the F1 <strong>and</strong><br />
F2 directions at both concentrations.<br />
Although a Gaussian peak shape is consistent with the HSQC spectra considered here, it is<br />
not an assumption <strong>of</strong> the peak picking genetic algorithm: instead, the theoretical peak shape is a<br />
parameter to the algorithm.<br />
3.2. Peak Width. From Figure 21, it can also be seen that the peak width is independent <strong>of</strong> the<br />
peak intensity.<br />
To verify this, the glycine peak width was measured in a series <strong>of</strong> HSQC spectra <strong>of</strong> mixtures<br />
<strong>of</strong> sucrose <strong>and</strong> glycine where the glycine concentration, <strong>and</strong> there<strong>for</strong>e the peak intensity, varied<br />
from lowest to highest by a factor <strong>of</strong> approximately 40. For each dimension, the two peak radii<br />
at quarter peak-height were measured. Since the spectra have discrete values, the quarter-height<br />
radius was estimated by linear interpolation. For example, if the peak maximum is Φ(fc), located<br />
at the discrete value fc, <strong>and</strong> the peak intensity falls below quarter <strong>of</strong> the height at the maximum<br />
between fr1 <strong>and</strong> fr2, where fr2 > fr1 > fc, then the estimate <strong>of</strong> the radius at quarter height, r0.25<br />
is given by:<br />
r0.25 = fr1 − fc + Φ(fr1) − 0.25Φ(fc)<br />
(fr2 − fr1) (3.2)<br />
Φ(fr1) − Φ(fr2)<br />
The radius at quarter-height was chosen in preference to the more traditional radius (or width)<br />
at half-height in order to provide more accuracy when calculating from discrete values: the radius<br />
at quarter-height is larger than the radius at half-height <strong>and</strong> so is subject to less error from linear<br />
interpolation <strong>and</strong> other calculations. For most peaks, it is still measured at a sufficiently high<br />
intensity to avoid the effect <strong>of</strong> noise.<br />
Figure 22 shows peak radii at quarter height plotted against peak intensity. In general, the<br />
slight variation in peak radius on the higher frequency side is the mirror image <strong>of</strong> that on the lower<br />
33<br />
(3.1)
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Intensity<br />
Intensity<br />
x 105<br />
20<br />
15<br />
10<br />
5<br />
0<br />
−5<br />
43.5<br />
x 105<br />
20<br />
15<br />
10<br />
5<br />
0<br />
−5<br />
43.5<br />
43<br />
43<br />
42.5<br />
42.5<br />
42<br />
42<br />
41.5<br />
41<br />
F 1 ( 13 C) / ppm<br />
40.5<br />
Experimental Peak<br />
Fitted Lorentzian Peak<br />
Fitted Gaussian Peak<br />
40<br />
39.5<br />
39<br />
Intensity<br />
x 106<br />
2.5<br />
2<br />
1.5<br />
1<br />
0.5<br />
0<br />
−0.5<br />
3.48<br />
3.46<br />
3.44<br />
3.42<br />
F 2 ( 1 H) / ppm<br />
(a) (b)<br />
41.5<br />
41<br />
F 1 ( 13 C) / ppm<br />
40.5<br />
Experimental Peak<br />
Fitted Lorentzian Peak<br />
Fitted Gaussian Peak<br />
40<br />
39.5<br />
39<br />
x 106<br />
2.5<br />
2<br />
1.5<br />
1<br />
0.5<br />
0<br />
−0.5<br />
3.48<br />
3.46<br />
3.44<br />
3.42<br />
F 2 ( 1 H) / ppm<br />
(c) (d)<br />
Intensity<br />
3.4<br />
3.4<br />
Experimental Peak<br />
Fitted Lorentzian Peak<br />
Fitted Gaussian Peak<br />
3.38<br />
Experimental Peak<br />
Fitted Lorentzian Peak<br />
Fitted Gaussian Peak<br />
Figure 21. Experimental peak shapes fitted to theoretical Lorentzian <strong>and</strong><br />
Gaussian peaks. The peak is the glycine peak in HSQC spectra <strong>of</strong> mixtures<br />
<strong>of</strong> sucrose (250 mM) <strong>and</strong> glycine. (a) <strong>and</strong> (b) show fitting in the F1 <strong>and</strong> F2<br />
directions respectively <strong>for</strong> a strong glycine peak from a sample concentration <strong>of</strong><br />
81 mM; (c) <strong>and</strong> (d) show the equivalent <strong>for</strong> a less intense peak from a sample <strong>of</strong><br />
concentration 12 mM.<br />
frequency side, <strong>and</strong> so the peak width (the sum <strong>of</strong> the two radii) remains constant <strong>for</strong> the same<br />
peak as the intensity changes. (The mirror-image pattern <strong>of</strong> radius variation can be explained by<br />
the ‘true’ central frequency <strong>of</strong> the peak moving slightly in each spectrum compared to the discrete<br />
grid <strong>of</strong> frequency values: the central frequency from which the radius is measured is the discrete<br />
value nearest to the ‘true’ value.)<br />
3.3. Peak Fit Metric. To assess the fit <strong>of</strong> a theoretical peak to the experimental peak, the<br />
following metric was chosen:<br />
<br />
(f1,f2)∈R<br />
ΩR =<br />
(Φ(f1, f2) − Θ(f1, f2)) 2<br />
<br />
(f1,f2)∈R Φ(f1, f2) 2<br />
(3.3)<br />
where Φ(f1, f2) <strong>and</strong> Θ(f1, f2) are the experimental <strong>and</strong> theoretical spectra respectively. R is the<br />
region <strong>of</strong> interest, <strong>and</strong> in practice this can cover a set <strong>of</strong> adjacent peaks (see section 3.6). Note<br />
that the metric is independent <strong>of</strong> the intensity scale <strong>and</strong> there<strong>for</strong>e gives equivalent measurements<br />
<strong>for</strong> large <strong>and</strong> small peaks.<br />
3.4. A Priori Knowledge Encapsulated in the Genetic Algorithm. Experimenters per<strong>for</strong>ming<br />
manual peak picking use a priori knowledge about peak shape to distinguish between<br />
peaks <strong>and</strong> noise artefacts. The GA attempts to capture the following aspects <strong>of</strong> this knowledge in<br />
its genome <strong>and</strong> operators.<br />
Radial Symmetry: Symmetry <strong>of</strong> peak shape is a criterion used by many automated peak<br />
picking techniques in multidimensional <strong>NMR</strong>[12]. The shape <strong>of</strong> Lorentzian (equation (3.1))<br />
is symmetrical about the centre frequency. This is also suggested by Figure 22 when the<br />
fluctuations in the discretized centre frequency value are accounted <strong>for</strong>. However, this<br />
does indicate that the GA must also determine a more accurate centre frequency if radial<br />
symmetry is to be accounted <strong>for</strong>.<br />
34<br />
3.38
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
F 1 Radius ( 13 C) / ppm<br />
F 2 Radius ( 1 H) / ppm<br />
0.8<br />
0.7<br />
0.6<br />
0.5<br />
0.4<br />
0.3<br />
0.2<br />
0.1<br />
Higher Frequency Radius<br />
Lower Frequency Radius<br />
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2<br />
x 10 6<br />
0<br />
Peak Intensity<br />
0.02<br />
0.018<br />
0.016<br />
0.014<br />
0.012<br />
0.01<br />
0.008<br />
0.006<br />
0.004<br />
0.002<br />
Higher Frequency Radius<br />
Lower Frequency Radius<br />
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2<br />
x 10 6<br />
0<br />
Peak Intensity<br />
Figure 22. Peak radii at quarter height <strong>for</strong> the glycine peak in HSQC spectra<br />
<strong>of</strong> mixtures <strong>of</strong> sucrose (250 mM) <strong>and</strong> glycine, the glycine concentration ranging<br />
from 4 mM to 160 mM. The peak radii <strong>for</strong> the higher <strong>and</strong> lower frequency sides <strong>of</strong><br />
the peak are plotted against peak intensity. (a) shows the radii in F1 dimension;<br />
(b) in F2 dimension.<br />
Peak Width: As discussed above, experimental <strong>and</strong> instrumental factors broaden the resonance<br />
frequency line to <strong>for</strong>m a peak. Thus peaks may be distinguished by a characteristic<br />
width. However, other processes, such as chemical exchange[14], can widen the peak further.<br />
Thus the GA can distinguish peaks from artefacts using the criterion <strong>of</strong> a peak width<br />
at or above a particular threshold, the value <strong>of</strong> which will be determined by the nature <strong>of</strong><br />
the <strong>NMR</strong> experiment <strong>and</strong> the processing <strong>of</strong> the FID.<br />
This criterion is significant when used in conjunction with the denoising algorithm<br />
defined in section 2.6. As can be seen in Figure 18, the denoising algorithm is particularly<br />
effective at reducing the amplitude <strong>of</strong> the noise at the sides (‘flanks’) <strong>of</strong> t1-noise ridges.<br />
This means that the peak width <strong>of</strong> noise artefacts in the relatively strong amplitude centre<br />
<strong>of</strong> the ridge will have their (quarter-height) peak widths significantly reduced, increasing<br />
the likelihood <strong>of</strong> rejection by the GA.<br />
Multiplets: As described in section A.5, spin-Ssin coupling gives rise to multiplets <strong>of</strong> peaks<br />
with intensities in specific ratio. If the distance between the peaks <strong>of</strong> the multiplet are<br />
less than the resolution <strong>of</strong> the <strong>NMR</strong> experiment <strong>and</strong> instrument, the individual peaks may<br />
not be distinguishable <strong>and</strong> instead a single broad peak, symmetrical, but different from<br />
the st<strong>and</strong>ard shape, may result. An example <strong>of</strong> such a peak shape is shown in Figure 23.<br />
35
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Intensity<br />
F 1 ( 13 C) / ppm<br />
12<br />
10<br />
8<br />
6<br />
4<br />
2<br />
0<br />
−2<br />
71<br />
x 10 5<br />
72<br />
73<br />
74<br />
3.68<br />
3.66<br />
3.64<br />
F 2 ( 1 H) / ppm<br />
Figure 23. Example a peak shape caused by a non-resolved multiplet in an<br />
HSQC spectrum <strong>of</strong> sucrose.<br />
The homonuclear spin-spin coupling constant <strong>for</strong> 1 H in the organic compounds present<br />
in a metabolome is dependent on the relative orientations <strong>of</strong> the two nuclei <strong>and</strong> the number<br />
<strong>of</strong> bonds (2 or more) separating them, but can range in magnitude from
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
2.5<br />
1.5<br />
0.5<br />
0<br />
3<br />
Offset from Centre F 1 ( 13 C)<br />
Frequency <strong>of</strong> Peak B / ppm<br />
Fit Metric<br />
0.5<br />
0.45<br />
0.4<br />
0.35<br />
0.3<br />
0.25<br />
0.2<br />
0.15<br />
0.1<br />
0.05<br />
0<br />
1<br />
Fit Metric<br />
2<br />
2<br />
1<br />
2<br />
3<br />
1<br />
Multiplet Degree<br />
0<br />
4<br />
−1<br />
−2<br />
5<br />
−0.15<br />
0.025<br />
−0.1<br />
0.02<br />
0.015<br />
−0.05<br />
0<br />
0.05<br />
Offset from Centre F 2 ( 1 H)<br />
Frequency <strong>of</strong> Peak A / ppm<br />
0.01<br />
0.005<br />
0<br />
0.1<br />
Multiplet Seperation along F 2 ( 1 H) / ppm<br />
Figure 24. Surface plots <strong>of</strong> the fitness <strong>of</strong> theoretical peak shapes against experimental<br />
peaks. A lower fit metric represents a better fit. In each case two <strong>of</strong> the<br />
theoretical peak parameters were varied, keeping all others constant. In (a), the<br />
experimental peak region contains two adjacent (<strong>and</strong> partially convoluted) peaks<br />
<strong>and</strong> the parameters varied are the centre F1 frequency <strong>of</strong> one peak <strong>and</strong> the centre<br />
F2 frequency <strong>of</strong> the other. In (b), the experimental region is a single peak consistent<br />
with a non-resolvable multiplet <strong>and</strong> the parameters varied are the multiplet<br />
degree <strong>and</strong> multiplet separation (equivalent to the spin-spin coupling constant).<br />
frequency <strong>of</strong> the other. As can be seen, the fitness l<strong>and</strong>scape has a distinct global minimum which<br />
should be quickly located by a GA.<br />
Figure 24(b) shows the fit to the non-resolvable multiplet shown in Figure 23. The parameters<br />
are the separation <strong>of</strong> the multiplet peaks <strong>and</strong> the degree <strong>of</strong> the multiplet. Here the fitness l<strong>and</strong>scape<br />
is more complicated, <strong>and</strong> while there is a global minimum it is more shallow <strong>and</strong> there are<br />
indications <strong>of</strong> rapidly changing fitness at larger multiplet separations. (Since other parameters,<br />
particularly accurate peak centre frequencies <strong>and</strong> widths are not varied in this calculation, <strong>and</strong><br />
may not be the optimum values, the multiplet degree <strong>and</strong> separation should not be inferred from<br />
this figure.)<br />
Note that the behaviour at higher multiplet separation (largely omitted from Figure 24 <strong>for</strong><br />
clarity <strong>of</strong> the global minimum) suggests that the a relatively good fit <strong>for</strong> an odd degree <strong>of</strong> multiplet<br />
37
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(triplet <strong>and</strong> quintiplet etc.) changes to a bad fit <strong>for</strong> an even degree (doublet, quadruplet etc.) <strong>and</strong><br />
vice versa. This might be expected since odd degree multiplets are symmetrical about the central<br />
peak in the multiplet, while even degree multiplets are symmetrical about a point midway between<br />
the two central peaks, resulting in distinctive shapes <strong>for</strong> each case, especially when the multiplet<br />
separation is large compared to the resolution in the spectrum.<br />
The two example fitness l<strong>and</strong>scapes, while being necessarily limited projections <strong>of</strong> the many<br />
dimensional search space, suggest that there are few local optima <strong>and</strong> so, with carefully designed<br />
operators to take account <strong>of</strong> behaviours such as that discussed <strong>for</strong> the multiplet degree, the GA<br />
will be a suitable technique to locate the global optimum.<br />
3.6. Identification <strong>of</strong> Convoluted Peak Regions. The GA is applied not to the entire spectrum<br />
in one go, but one at a time to ‘regions’ <strong>of</strong> the spectra that consist <strong>of</strong> adjacent, <strong>and</strong> there<strong>for</strong>e<br />
potentially convoluted, peaks. Each <strong>of</strong> these regions is ‘isolated’ from the rest <strong>of</strong> the spectrum<br />
<strong>and</strong> so can theoretical peak fitting can take place independently on each region.<br />
The experimental peaks are initially determined from the spectrum by finding local maxima in<br />
the denoised spectrum. (In practice, additional criteria are applied to improve per<strong>for</strong>mance - this<br />
is discussed in section 4.)<br />
Next, the watershed region <strong>of</strong> each peak is identified. The watershed region is essentially the<br />
contiguous area around the peak in which hill-climbing would end up at the peak maximum <strong>and</strong><br />
so defines the unique ‘area’ <strong>of</strong> the peak. The watershed region is bounded by ‘valleys’ after which<br />
the surface rises to meet another peak. For convoluted peaks, this boundary may actually be at<br />
a significant height (intensity) in the sector <strong>of</strong> the boundary common to the two peaks.<br />
Technically, the region located is the watershed <strong>of</strong> the negative spectrum, i.e. <strong>of</strong> −Φ(f1, f2), but<br />
the term ‘watershed’ is used here <strong>for</strong> brevity. In the context <strong>of</strong> the negative spectrum, the term<br />
watershed is a more accurate geophysical analogy: the watershed is the region <strong>of</strong> the spectrum in<br />
which ‘rainfall’ would collect in the peak (now a ‘depression’ in the negative spectrum).<br />
The implementation <strong>of</strong> the GA uses matlab’s default watershed algorithm that is a variation<br />
<strong>of</strong> the Vincent <strong>and</strong> Soille algorithm[16]. When applied to the entire (negative) spectrum, the<br />
algorithm locates the discrete frequency grid points belonging to the watershed <strong>of</strong> each peak.<br />
The boundary ‘valleys’ are common to more than one peak <strong>and</strong> so the grid points <strong>for</strong>ming the<br />
boundaries do not belong to any watershed.<br />
For practical reasons, discussed in sections 3.9 <strong>and</strong> 4, the watershed area identified is modified<br />
to consist <strong>of</strong> those points that are a certain percentage, θw, <strong>of</strong> the peak height or above. In other<br />
words, the watershed does not extend all the way to the valley floor. This is implemented by<br />
removing those points below the height threshold from the ‘full’ watershed, <strong>and</strong> then filling in any<br />
‘holes’ in the resulting pattern <strong>of</strong> grid points.<br />
To identify convoluted peak regions, the watershed <strong>of</strong> the spectrum is processed so that all grid<br />
points that are in a watershed, or within a distance <strong>of</strong> 1 grid unit (using the ‘cityblock’ distance<br />
metric) <strong>of</strong> a watershed, are identified. The distance criterion includes the common watershed<br />
boundaries within the region. The resulting set <strong>of</strong> grid points is then used to identify contiguous<br />
regions (using matlab’s bwlabel function). Each region consists <strong>of</strong> peaks with common boundaries,<br />
<strong>and</strong> that are there<strong>for</strong>e potentially convoluted, <strong>and</strong> each region is isolated in the sense that<br />
it shares no boundary with other regions.<br />
3.7. Genetic Algorithm Representation, Operators <strong>and</strong> Objective Function. This section<br />
describes, in functional terms, the specifics <strong>of</strong> the genetic algorithm used <strong>for</strong> fitting a single<br />
convoluted peak region. The implementation details are described in section 3.8 below.<br />
3.7.1. Genome. In the GA, the genome represents a number, Np, <strong>of</strong> peaks in a convoluted peak<br />
regions. For each peak p in this convoluted peak region, the genome stores the following variables:<br />
• The location <strong>of</strong> peak centre in terms <strong>of</strong> F1 <strong>and</strong> F2 frequencies, fc;1 <strong>and</strong> fc;2 respectively.<br />
Note that the location <strong>of</strong> the peak is a real value, <strong>and</strong> is not restricted to the discrete<br />
frequency grid <strong>of</strong> the spectrum.<br />
• The peak height (maximum intensity), h.<br />
38
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
• The peak widths at quarter peak height in the F1 <strong>and</strong> F2 dimension, w0.25;1 <strong>and</strong> w0.25;2.<br />
The widths also apply to the individual peaks in a (non-resolvable) multiplet. Again, the<br />
widths are not restricted to the discrete frequency grid spacing.<br />
• The degree <strong>of</strong> multiplet in both dimensions, m1 <strong>and</strong> m2, <strong>and</strong> the corresponding separations<br />
j1 <strong>and</strong> j2. (Although, as discussed above, multiplets will not be permitted in the 13 C<br />
dimension, F1 <strong>for</strong> spectra considered here.)<br />
3.7.2. Initialisation Operator. The genomes <strong>of</strong> the initial population in the GA are initialised<br />
using estimated values derived from the experimental spectrum. The peak centre frequencies, fc;1<br />
<strong>and</strong> fc;2, are the coordinates on the discrete frequency grid <strong>of</strong> the peak maximum. For each peak<br />
in the region, the height, h, is taken from the intensity at the peak centre. The widths, w0.25;1<br />
<strong>and</strong> w0.25;2, are initialised to the interpolated values described in section 3.2 above. (As seen in<br />
Figure 22, this may include a small error resulting from the discrete nature <strong>of</strong> the peak centre<br />
location.) The F2 multiplet degree, m2, is initially set to 1, indicating no multiplet.<br />
Immediately after setting the values from the experimental spectrum, the genome is mutated<br />
using the mutation operator below so that there is variance in the initial GA population.<br />
3.7.3. Mutation Operator. The mutation operator makes r<strong>and</strong>om changes to the genome <strong>of</strong> a single<br />
individual.<br />
For each peak, individual genome variables are using mutated using a zero-meaned Normal distribution<br />
with the st<strong>and</strong>ard deviation controlled by the variable itself, or another genome variable,<br />
in conjunction with a multiplier.<br />
fc;1 = fc;1 + ∆f1 where ∆f1 ∼ N(0, kfw0.25;1) (3.4)<br />
fc;2 = fc;2 + ∆f2 where ∆f2 ∼ N(0, kfw0.25;2) (3.5)<br />
h = h + ∆h where ∆h ∼ N(0, khh) (3.6)<br />
w0.25;1 = w0.25;1 + ∆w1 where ∆w1 ∼ N(0, kww0.25;1) (3.7)<br />
w0.25;2 = w0.25;2 + ∆w2 where ∆w2 ∼ N(0, kww0.25;2) (3.8)<br />
j2 = j2 + ∆j2 where ∆j2 ∼ N(0, kjj2) (3.9)<br />
The multipliers kf,kh,kw, <strong>and</strong> kj, are parameters <strong>of</strong> the GA as a whole.<br />
The multiplet degree variable, m2, is modified according the equation:<br />
⎧<br />
⎪⎨ U(0, (m2 − 1)) m = 1<br />
m2 = m2 + round(∆m2) where ∆m2 ∼ −(2 + N(0, 0.5) m > 1 <strong>and</strong> χ ≤ 0.5 (3.10)<br />
⎪⎩<br />
(2 + N(0, 0.5) m > 1 <strong>and</strong> χ > 0.5<br />
where U(a, b) denotes the uni<strong>for</strong>m distribution between a <strong>and</strong> b, m2 is the maximum multiplet<br />
degree allowed, χ is a r<strong>and</strong>om variable uni<strong>for</strong>mly distributed between 0 <strong>and</strong> 1, <strong>and</strong> the round(·)<br />
operator returns the nearest integer. The effect <strong>of</strong> this mutation is to r<strong>and</strong>omly set the multiplet<br />
degree if it is currently 1 (indicating no multiplet), otherwise to encourage changes in the multiplet<br />
degree <strong>of</strong> ±2 to move sensibly in the fitness l<strong>and</strong>scape <strong>for</strong> multiplets as described in section 3.5.<br />
(Note that if m2 is currently 1 <strong>and</strong> is mutated to a higher value, then the separation j2 is set to<br />
an initial value determined by another parameter <strong>of</strong> the GA).<br />
All the genome variables have a range <strong>of</strong> allowable values, set by parameters <strong>of</strong> the GA, from<br />
a priori knowledge where appropriate. For the example, the range <strong>of</strong> the multiplet separation,<br />
j2 is defined by the range <strong>of</strong> the homonuclear 1H coupling constant presented in section 3.4. If<br />
mutation results in a value outside <strong>of</strong> the range, the usual correction is to set the variable to the<br />
closest range limit.<br />
A further mutation operates on the genome as a whole to create a new peak. A r<strong>and</strong>om peak is<br />
chosen <strong>and</strong> split into two (the height <strong>of</strong> each being half that <strong>of</strong> the original). The centre frequencies<br />
<strong>of</strong> the two new peaks are symmetrical arranged around the centre <strong>of</strong> the old peak, the separations<br />
in each dimension being chosen according a Normally-distributed r<strong>and</strong>om variable.<br />
39
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Each <strong>of</strong> the possible mutations occur independently with a chosen probability. This probability<br />
is parameterised according to the type <strong>of</strong> mutation: <strong>for</strong> example the mutation to produce a new<br />
peak is generally set low to avoid fitting noise artefacts using a large number <strong>of</strong> small peaks.<br />
3.7.4. Crossover Operator. The crossover operator takes two parents, A <strong>and</strong> B, <strong>and</strong> produces one<br />
or two children, C <strong>and</strong> D, by combining the genomes <strong>of</strong> A <strong>and</strong> B.<br />
Since the number <strong>of</strong> peaks in A <strong>and</strong> B may be different—owing to the mutation that can split<br />
peaks—the crossover operation is more complicated than normal crossover where the genome size<br />
is constant. The solution is to choose pairs <strong>of</strong> peaks, one from A <strong>and</strong> the other from B, that are<br />
closest <strong>and</strong> per<strong>for</strong>m crossover on each pair individually, as follows.<br />
For each peak, a in A in turn, the closest peak b is located. The resulting variables <strong>for</strong> peak c<br />
in the child are derived as:<br />
f (c) 1<br />
c;1 = 2 (f(a) c;1<br />
f (c) 1<br />
c;2 = 2 (f(a) c;2<br />
+ f(b) c;1 ) (3.11)<br />
+ f(b) c;2 ) (3.12)<br />
h (c) = 1<br />
2 (h(a) + h (b) ) (3.13)<br />
w (c) 1<br />
0.25;1 = 2 (w(a) 0.25;1 + w(b) 0.25;1 ) (3.14)<br />
w (c)<br />
0.25;2<br />
= 1<br />
m (c)<br />
2 =<br />
j (c)<br />
2<br />
2 (w(a) 0.25;2<br />
<br />
⌈1 2 (m(a) 2<br />
⌊1 2 (m(a) 2<br />
1 = 2 (j(a) 2<br />
+ w(b) 0.25;2 ) (3.15)<br />
+ m(b) 2 )⌉ m(a) 2 > m(b) 2<br />
+ m(b)<br />
2<br />
)⌋ m(a)<br />
2<br />
≤ m(b)<br />
2<br />
(3.16)<br />
+ j(b) 2 ) (3.17)<br />
This results in child C having the same number <strong>of</strong> peaks as the parent A. If a second child, D, is<br />
required (which is the normal behaviour), it is derived by reversing the roles <strong>of</strong> A <strong>and</strong> B in the<br />
above.<br />
3.7.5. Objective Function. The objective function, η, uses the peak fit metric, Ω, defined in (3.3):<br />
η = ΩR + 1<br />
N ′ p<br />
N ′<br />
p<br />
<br />
i=1<br />
ΩWi<br />
(3.18)<br />
where R is the entire convoluted peak region, N ′ p the number <strong>of</strong> peaks in the experimental region<br />
(i.e. the initial number be<strong>for</strong>e mutation), <strong>and</strong> Wi the corresponding experimental watersheds<br />
described above.<br />
The purpose <strong>of</strong> this definition is to fit each peak as closely as possible, but also to fit the entire<br />
region. The latter condition prevents additional peaks being created (unnecessarily) outside any<br />
individual peak watershed.<br />
The GA is set to minimise the value <strong>of</strong> η <strong>for</strong> the region, corresponding to a good fit.<br />
3.7.6. Rationalisation Function. After any change to a genome’s variables (mutation) or the creation<br />
<strong>of</strong> a new genome (initialisation <strong>and</strong> crossover), a rationalisation function is called. This<br />
per<strong>for</strong>ms three operations:<br />
• If two or more peaks in a genome are very close together, they are combined to <strong>for</strong>m a<br />
single peak.<br />
• If the multiplet spacing has become very small compared to the peak width, the multiplet<br />
degree is reset to 1 (indicating no multiplet).<br />
• If any new peaks are substantially outside the original convoluted peak region, they are<br />
removed. This is largely <strong>for</strong> technical reasons as it ensures that the size <strong>of</strong> matrices involved<br />
are kept within sensible limits.<br />
40
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
3.7.7. Termination Condition. The GA terminates on any <strong>of</strong> the following conditions:<br />
• When the best individual in the population satisifies both (a) its regional fit, ΩR in (3.18),<br />
is below a specified theshold, <strong>and</strong> (b), the fit metric <strong>of</strong> every peak within its watershed,<br />
ΩWi, is below a second threshold.<br />
• After a set number <strong>of</strong> generations is reached.<br />
• Convergence <strong>of</strong> the best individual, i.e. if over a set number <strong>of</strong> generations, η <strong>for</strong> the best<br />
individual in each generation does not change more than a defined proportion.<br />
3.8. Technical Implementation.<br />
3.8.1. matlab <strong>and</strong> GAlib Combination. The genetic algorithm itself is implemented using a C ++<br />
library called GAlib that provides a framework <strong>for</strong> creating <strong>and</strong> customising GAs[25]. The manipulation<br />
required in (a) setting up the genome by identifying peaks <strong>and</strong> deriving watershed <strong>for</strong> each<br />
convoluted peak region, <strong>and</strong> (b) calculating the fit metric <strong>of</strong> theoretical peaks to experiment peaks,<br />
is most appropriately per<strong>for</strong>med in matlab as both stages use matrices representing experimental<br />
<strong>and</strong> theoretical spectra. The two tools—GAlib <strong>and</strong> matlab—are combined using MEX files.<br />
Having identified a specific convoluted peak region <strong>and</strong> established the experimental values <strong>of</strong><br />
the genome variables in matlab, a MEX file is called that uses GAlib to instantiate <strong>and</strong> run the<br />
algorithm itself. Each time the algorithm evaluates the fit metric <strong>for</strong> a peak region, the C ++code<br />
in the MEX file calls back to matlab to run the m-file that implements the metric.<br />
3.8.2. Custom GAlib Genome Class. The peak shape is implemented as a C ++ class that subclasses<br />
the genome object in GAlib. The class defines the genome variables. The class methods <strong>and</strong><br />
related functions implement the initialisation, mutation, <strong>and</strong> crossover operators described above,<br />
<strong>and</strong> calls back to matlab to evaluate the objective function.<br />
3.8.3. GAlib Parameters. To enable setting <strong>of</strong> st<strong>and</strong>ard GAlib parameters, such as: number <strong>of</strong><br />
generations, size <strong>of</strong> population, crossover rate etc., a single string parameter is passed from matlab<br />
which is in the <strong>for</strong>mat <strong>of</strong> the comm<strong>and</strong> line parameters that would be passed to GAlib running<br />
as a st<strong>and</strong>alone program. The MEX file tokenises the string into an array <strong>of</strong> string representing<br />
each parameter <strong>and</strong> passed to GAlib as if it were the comm<strong>and</strong> line string argument to the main()<br />
function.<br />
3.8.4. Efficient Calculation <strong>of</strong> Fit Metric. The fit metric is called any time a genome is created<br />
or any <strong>of</strong> its variables are changed, <strong>and</strong> so may be evaluated many times during a run <strong>of</strong> the GA.<br />
To ensure that the calculation is as efficient as possible, the following implementation is used:<br />
• The 3D shape <strong>of</strong> the theoretical peak is calculated once be<strong>for</strong>e calling the GA (actually<br />
once per spectrum be<strong>for</strong>e the GA is run individually on each convoluted peak region) <strong>and</strong><br />
stored as a matrix. This avoids time-consuming calculations if the peak is an analytical<br />
function, such as the Gaussian identified in section 3.1. 6<br />
The peak is calculated on a discrete grid that is substantially finer than <strong>of</strong> the experimental<br />
spectrum itself. When a value on the theoretical peak is required, the closest point<br />
on the fine grid is calculated <strong>and</strong> the value returned.<br />
• Constant values <strong>and</strong> matrices used in the fitness calculation—such as the theoretical peak<br />
shape matrix, the region <strong>and</strong> individual peak watersheds, <strong>and</strong> the value <strong>of</strong> the denominator<br />
in equation (3.3)—are passed to the GA <strong>and</strong> passed through to the fit metric calculation<br />
implemented in matlab.<br />
3.9. Results <strong>and</strong> Discussion. Figure 25 shows the results <strong>of</strong> pick peaking by the GA on a<br />
denoised HSQC spectrum <strong>of</strong> sucrose. For practical reasons, discussed in section 4, the list <strong>of</strong> peaks<br />
is first limited by thresholds on the SNR, but in this example the thresholds are relatively low (4<br />
times the thermal noise <strong>and</strong> 3 times the t1-noise) so as to include some artefacts from the t1-noise<br />
ridges <strong>and</strong> elsewhere. The threshold values <strong>for</strong> the fit metric were 0.001 <strong>for</strong> both the region <strong>and</strong><br />
individual peaks. The GA used a population <strong>of</strong> size 40 <strong>and</strong> a maximum <strong>of</strong> 500 generations.<br />
6 The method also allows other peak shape to be easily changed <strong>for</strong> a different analytical function, a peak shaped<br />
derived experimentally, <strong>and</strong>/or using different peak shapes in the two spectral dimensions.<br />
41
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Figure 25. Example <strong>of</strong> pick peaking by genetic algorithm on a section <strong>of</strong> a<br />
denoised HSQC spectrum <strong>of</strong> sucrose. The watersheds <strong>of</strong> peaks that are fitted<br />
to the theoretical peak shape by the GA are shown in mid-grey; peaks that are<br />
excluded by the GA are shown in black.<br />
The GA has correctly fitted the major peaks. However, even with the small threshold <strong>for</strong> the fit<br />
metric (requiring very good fits), the GA has also fitted many other peaks including some in the<br />
t1-noise streak. For many <strong>of</strong> the small peaks that the GA fits, it is difficult to distinguish, by eye, a<br />
difference in shape from the theoretical shape: an example <strong>of</strong> such a peak is shown in Figure 26(a).<br />
While some <strong>of</strong> these small peaks may be ‘genuine’ peaks resulting from low concentration <strong>of</strong> other<br />
compounds (contaminants) in the sample, it is suspected that many are simply noise artefacts,<br />
<strong>and</strong> that the GA is unable to distinguish between the shape <strong>of</strong> (some) noise artefacts <strong>and</strong> ‘genuine’<br />
peaks using the criteria listed in section 3.4.<br />
Nevertheless, the GA has identified some peaks that cannot be fitted with the theoretical peak<br />
shape. An example <strong>of</strong> a region containing two such peaks is shown in Figure 26(b), <strong>and</strong> visually<br />
it looks distinct from the theoretical peak shape.<br />
Figure 27(a) shows the results <strong>of</strong> the GA on a spectrum <strong>of</strong> a metabolic sample using the same<br />
parameters as <strong>for</strong> Figure 25. Here the GA incorrectly determines that some <strong>of</strong> the larger ‘genuine’<br />
peaks are not fitted to the theoretical peak shape. The reason <strong>for</strong> this is the significantly larger<br />
number <strong>of</strong> peaks in the spectrum resulting in regions with many convoluted peaks. This leads to<br />
a very high dimensional search space in which the GA is unable to fit every peak in the region<br />
within a practical number <strong>of</strong> generations.<br />
This effect can be minimised by modifying the parameters. Firstly, setting a slightly higher<br />
SNR threshold <strong>for</strong> peak identification reduces the overall number <strong>of</strong> peaks considered by the<br />
GA. Secondly, by increasing the boundary <strong>of</strong> the watershed as a ratio <strong>of</strong> the peak height (θw in<br />
section 3.6), peaks need to be more convoluted be<strong>for</strong>e being considered part <strong>of</strong> the same region,<br />
reducing the number <strong>of</strong> peaks per region. Finally, setting a higher threshold on the fit metric<br />
relaxes the closeness <strong>of</strong> the fit required.<br />
42
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
Intensity<br />
Intensity<br />
5000<br />
4000<br />
3000<br />
2000<br />
1000<br />
0<br />
−1000<br />
−2000<br />
6000<br />
4000<br />
2000<br />
0<br />
−2000<br />
−4000<br />
34<br />
71.5<br />
33.5<br />
72<br />
72.5<br />
33<br />
F 1 ( 13 C) / ppm<br />
F 1 ( 13 C) / ppm<br />
73<br />
32.5<br />
73.5<br />
32<br />
74<br />
5.16<br />
4.55<br />
5.18<br />
4.5<br />
5.2<br />
F 2 ( 1 H) / ppm<br />
4.45<br />
F 2 ( 1 H) / ppm<br />
Figure 26. (a) is an example <strong>of</strong> a small (SNR ≈ 3) peak in a denoised HSQC<br />
spectrum <strong>of</strong> sucrose that the GA fitted to the theoretical shape; (b) shows a region<br />
<strong>of</strong> two small convoluted peaks (SNR ≈ 3 <strong>and</strong> 4.5) in the same spectrum that was<br />
not successfully fitted by the GA.<br />
Figure 27(b) shows the effect when the SNR threshold is increased (from 3 to 4), the watershed<br />
boundary is changed from 10% to 20% <strong>of</strong> peak height, <strong>and</strong> the fit metric threshold is changed from<br />
0.001 to 0.01. In this case, many more <strong>of</strong> the larger ‘genuine’ peaks are fitted within the threshold,<br />
but the relaxation <strong>of</strong> the fit metric threshold means that fewer noise artefacts are identified as<br />
such.<br />
An alternative solution might be to modify the way in which the algorithm fits each region.<br />
Instead <strong>of</strong> attempting to fit all peaks in the region simultaneously, the algorithm could fit the<br />
largest peaks first <strong>and</strong> then move on to the smaller peaks. This would reduce the dimensionality<br />
<strong>of</strong> the search space at each stage, potentially resulting in better fits in a reasonable number <strong>of</strong><br />
generations <strong>for</strong> highly convoluted regions. 7<br />
The results suggest that the genetic algorithm is good <strong>for</strong> peak picking in relatively simple<br />
spectra such as sucrose, although it appears too optimistic in that it identifies too many small<br />
peaks as being ‘genuine’ rather than noise artefacts. 8 Given the similarity in shape between<br />
case.<br />
7 This alternative method was not tested owing to time constraints.<br />
8 A full analysis <strong>of</strong> each <strong>of</strong> the small peaks fitted by the GA would be required to be sure whether this was the<br />
43<br />
5.22<br />
4.4
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
Figure 27. Example <strong>of</strong> pick peaking by genetic algorithm on a section <strong>of</strong> a<br />
denoised HSQC spectrum <strong>of</strong> metabolomic sample derived from peas. The watersheds<br />
<strong>of</strong> peaks that are fitted to the theoretical peak shape by the GA are shown<br />
in mid-grey; peaks that are excluded by the GA are shown in black. (a) shows<br />
the fit using a fit metric threshold <strong>of</strong> 0.001; (b) shows the fit using a threshold <strong>of</strong><br />
0.01, a higher peak SNR threshold <strong>and</strong> a modified watershed boundary fraction.<br />
In can be seen that more <strong>of</strong> the large peaks are correctly fitted (grey) in (b) than<br />
(a), but fewer noise artefacts (black) are identified.<br />
‘genuine’ peaks <strong>and</strong> some noise artefacts, peak picking based purely on the peak shape might not<br />
be feasible. (It may, however, be useful in identifying artefacts introduced during denoising if,<br />
<strong>for</strong> example, wavelet noise separation were used instead <strong>of</strong> the direct signal thresholding used <strong>for</strong><br />
these spectra.)<br />
44
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
In more complicated metabolomic samples, the GA parameters need to be relaxed in order to<br />
fit highly convoluted regions within a reasonable number <strong>of</strong> generations, with the result that very<br />
few noise artefacts are identified as such.<br />
It should also be noted that the GA encapsulates only some <strong>of</strong> the a priori knowledge about<br />
peak shapes. For example, it considers only simplest multiplet structures rather than the more<br />
complicated structures resulting from different two or more different spin-spin coupling constants.<br />
However, by combining the GA peak picking with a more traditional SNR-based peak picking<br />
method (although modified to be adaptive to t1-noise ridges), some <strong>of</strong> the shortcomings <strong>of</strong> the<br />
GA with regard to metabolomic samples could be ameliorated while retaining the ability to locate<br />
noise artefacts. This approach is described in the next section.<br />
45
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
4. Combined <strong>Denoising</strong> <strong>and</strong> Peak Picking Process<br />
This section describes a process that combines the denoising algorithm with a hybrid genetic<br />
algorithm / SNR threshold peak picking method. It also describes how the processing derives some<br />
parameters <strong>of</strong> the denoising algorithm <strong>and</strong> peak picking genetic algorithm (GA) from the spectrum<br />
itself in order to minimise the number <strong>of</strong> parameters that must be specified to the process. The<br />
output <strong>of</strong> the process is a ‘clean’ <strong>2D</strong> spectrum free <strong>of</strong> noise that is suitable <strong>for</strong> use in the adaptive<br />
binning analysis described later.<br />
4.1. Implementation Overview. The processing consists <strong>of</strong> an ‘umbrella’ matlab script to<br />
the denoising algorithm <strong>and</strong> GA peak picking code described in earlier sections. The script calls<br />
other functions implemented as matlab m-files as well as MEX files (written in C ++). The latter<br />
(a) load the <strong>NMR</strong> spectrum from Bruker Topspin processed data files, (b) implement the genetic<br />
algorithm, <strong>and</strong> (c) optionally save the processed <strong>NMR</strong> spectrum back to Bruker Topspin data<br />
files. The code structure is detailed in appendix E.<br />
A structure variable is used to control which <strong>of</strong> the processing steps are per<strong>for</strong>med. This enables<br />
flexibility in the type <strong>of</strong> processing, <strong>for</strong> example skipping the t1-noise denoising step in order to<br />
compare results with <strong>and</strong> without denoising. The control structure is also set by the processing<br />
itself so that if a step should fail, the process restarts at the failed step without repeating earlier<br />
steps unnecessarily.<br />
A second structure contains the parameters used by the processing steps, such as the denoising<br />
threshold multipliers <strong>and</strong> GA operator parameters.<br />
Both the control <strong>and</strong> parameters structure are initially set to default values which are then<br />
amended by custom functions that are named in variables passed to the processing script. This<br />
enables reusable ‘parameter sets’, defined as m-file functions, suitable <strong>for</strong> a range <strong>of</strong> spectra.<br />
The output <strong>of</strong> the processing script includes the matrices representing the original, denoised<br />
<strong>and</strong> ‘clean’ spectra <strong>and</strong> a data structure listing each peak. Each record in the structure contains<br />
details including the peak location, height (intensity), radii at quarter-height, SNR, the best fit<br />
metric obtained by the GA, <strong>and</strong> whether the peak was picked <strong>for</strong> inclusion in the ‘clean’ spectrum.<br />
The resulting spectra can optionally be saved to file in the Bruker Topspin data <strong>for</strong>mat.<br />
4.2. Processing Steps.<br />
1 - Load Spectrum: The data files containing the (F2 real; F1 real) <strong>and</strong> (F2 imaginary;<br />
F1 real) parts <strong>of</strong> the spectrum are loaded from the Bruker Topspin processed data files.<br />
(At this point, a region <strong>of</strong> the spectrum, e.g. a subset <strong>of</strong> the F2 range, can be extracted<br />
<strong>and</strong> used <strong>for</strong> subsequent processing if the entire spectrum is not required. This can limit<br />
the success <strong>of</strong> denoising since there are fewer t1-noise ridges to correlate, but is useful <strong>for</strong><br />
analysing a localised feature quickly since a smaller set <strong>of</strong> data improves per<strong>for</strong>mance.)<br />
2 - Derive Minimum Peak Width: This optional step identifies peaks in the ‘noisy’ spectrum<br />
(the original spectrum be<strong>for</strong>e any denoising) using the technique used later, in step<br />
5, on the denoised spectrum. However, the SNR threshold used to identify peaks is twice<br />
that used <strong>for</strong> the denoised spectrum so as to avoid identifying any noise artefacts. (Note<br />
this is the identification <strong>of</strong> local maxima above an SNR threshold, but not the picking<br />
<strong>of</strong> peaks, i.e. the distinguishing <strong>of</strong> small peaks from noise artefacts using the GA.) The<br />
radii <strong>of</strong> the peaks are measured <strong>and</strong> then used to derive the minimum peak widths in the<br />
F1 <strong>and</strong> F2 dimensions. These widths are used to set parameters <strong>for</strong> both the denoising<br />
algorithm <strong>and</strong> the GA.<br />
Alternatively, the minimum peak widths can be set directly from parameters, thus<br />
avoiding this sometimes time-consuming step. Setting the minimum peak widths directly<br />
from parameters is appropriate <strong>for</strong> a set <strong>of</strong> similar <strong>NMR</strong> experiments (with the same<br />
processing parameters), if the widths have been already been derived <strong>for</strong> one representative<br />
experiment.<br />
3 - Separate Noise: This step implements the direct signal thresholding separation <strong>of</strong> t1noise,<br />
described in section 2.3.4, on the complex spectrum <strong>for</strong>med by combining the real<br />
<strong>and</strong> imaginary parts. Optionally, wavelet denoising may used as an alternative. The<br />
46
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
results are ‘peak’ <strong>and</strong> ‘noise’ spectra, with the noise spectrum containing the majority <strong>of</strong><br />
the t1-noise <strong>and</strong> some <strong>of</strong> the intensity <strong>of</strong> small peaks convoluted with the noise.<br />
4 - Apply <strong>Denoising</strong> Algorithm: The denoising algorithm described in section 2.6 is applied<br />
to the complex noise spectrum. The peak widths derived in step 2 are used to set<br />
parameters <strong>of</strong> the algorithm as shown in Table 1. The result <strong>of</strong> this step is the ‘denoised’<br />
spectrum defined by equation (2.26) consisting <strong>of</strong> ‘genuine’ peaks with much <strong>of</strong> the t1-noise<br />
removed.<br />
5 - Identify Peaks in Denoised Spectrum: This step is the equivalent <strong>of</strong> step 2, but<br />
applied now to the denoised spectrum. Peaks are identified as local maxima in the real<br />
component <strong>of</strong> the spectrum, considering all 8 neighbouring data points.<br />
A peak is not recorded if its intensity is below thresholds defined in terms <strong>of</strong> the SNR.<br />
The first threshold, τthermal, considers the SNR measured with respect to the st<strong>and</strong>ard<br />
deviation <strong>of</strong> the thermal noise, essentially the background noise that—unlike the t1-noise—<br />
occurs across the entire spectrum. An estimate <strong>of</strong> the thermal noise is made by taking<br />
the minimum interquartile range (iqr) <strong>of</strong> F1 traces considered across the entire F2 range,<br />
thereby picking a trace does not include t1-noise. The thermal noise <strong>of</strong> a peak is then<br />
calculated using this iqr in an amended <strong>for</strong>m <strong>of</strong> equation (2.28).<br />
The second threshold, τt1, considers the actual SNR <strong>of</strong> the peak, calculated by equation<br />
(2.28). Since this SNR is calculated using the iqr <strong>of</strong> the F1 trace containing the peak<br />
maximum, the SNR is calculated with respect to the t1-noise.<br />
The thresholds set <strong>for</strong> these two SNR values are designed to discard peaks whose SNR<br />
is too low <strong>for</strong> the peak to be realistically distinguished from noise artefacts. Typical values<br />
<strong>for</strong> each threshold are τthermal = 4 <strong>and</strong> τt1 = 3, equivalent to a peak intensities that fall<br />
within the 99.99% <strong>and</strong> 99.73% confidence limits, respectively, <strong>of</strong> the noise distributions, if<br />
the noise is assumed to be normally distributed in the real spectrum (section 2.3.1).<br />
The thresholds are implemented partly <strong>for</strong> per<strong>for</strong>mance reasons: without the thresholds,<br />
the number <strong>of</strong> peaks considered is extremely large compared to the actual number <strong>of</strong><br />
‘genuine’ peaks <strong>and</strong> this significantly slows the processing <strong>of</strong> later steps. It also <strong>for</strong>ms part<br />
<strong>of</strong> the hybrid peak picking method, combining the genetic algorithm peak fitting with<br />
SNR thresholds: it sets a lower limit <strong>for</strong> SNR.<br />
In addition, peaks that are within a certain distance <strong>of</strong> the edges <strong>of</strong> the spectrum<br />
are also omitted to exclude artefacts that can result from processing <strong>of</strong> the <strong>NMR</strong> spectrum.<br />
Examples <strong>of</strong> these artefacts can be seen at the top <strong>and</strong> bottom <strong>of</strong> t1-noise ridges in<br />
Figure 17(a). Since they are not correlated across t1-noise ridges, they can remain after<br />
denoising as can be seen in part (b) <strong>of</strong> the same figure. (If wavelet denoising is used to separate<br />
the t1-noise, this can also introduce edge artefacts owing to artificial discontinuities<br />
by processing equivalent to ‘wraparound’: see section B.5.4.)<br />
For the peaks above the thresholds, the location, SNR, <strong>and</strong> peak radii are measured<br />
<strong>and</strong> recorded. In addition, both the full watershed region <strong>of</strong> the peak, <strong>and</strong> the watershed<br />
bounded at a fraction <strong>of</strong> the peak height, are recorded. The derivation <strong>of</strong> the latter<br />
watershed is described in section 3.6, <strong>and</strong> uses a parameter, θw, to determine the fraction<br />
<strong>of</strong> the peak height at which the watershed boundary occurs.<br />
6 - Identify Convoluted Peak Regions: This step identifies regions <strong>of</strong> peaks that are<br />
adjacent to one another, <strong>and</strong> there<strong>for</strong>e potentially convoluted. The process is described in<br />
section 3.6. The output <strong>of</strong> this step is a set <strong>of</strong> regions that are isolated from one another<br />
in the spectrum, within which the peaks are convoluted.<br />
7 - Fit Peaks Using GA: In this step, the genetic algorithm described in section 3.7 is applied<br />
to each region identified in the preceding step, in turn. The peak widths determined<br />
in step 2 are again used to set parameters to the GA, this time setting a lower limit <strong>for</strong><br />
the mutation <strong>of</strong> widths in the genome. The best fit metric determined by the algorithm<br />
is stored <strong>for</strong> each peak.<br />
8 - Pick Peaks: This step implements a hybrid <strong>of</strong> the GA <strong>and</strong> SNR-based peak picking<br />
methods to overcome some <strong>of</strong> the practical limitations <strong>of</strong> the GA peak picking process <strong>for</strong><br />
metabolic samples.<br />
47
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
As discussed in section 3.9, a GA using a practical number <strong>of</strong> generations is sometimes<br />
unable to fit even the intense peaks in regions consisting <strong>of</strong> a large number <strong>of</strong> convoluted<br />
peaks. Since the largest peaks are clearly ‘genuine’ rather than noise, a pragmatic solution<br />
is to automatically consider the largest peaks as ‘genuine’ <strong>and</strong> only consider the fit <strong>of</strong> the<br />
smaller peaks when peak picking.<br />
Thus a further SNR threshold, τinclude, is used <strong>for</strong> this peak picking. Peaks whose<br />
SNR—measured against the trace containing the peaks, <strong>and</strong> there<strong>for</strong>e accounting <strong>for</strong><br />
changes in t1-noise amplitude—is above the threshold are picked. Peaks below this threshold<br />
may also be picked if the fit metric determined by the GA is below a threshold, indicating<br />
a close fit. (Note that the very smallest peaks have already been excluded by the<br />
two thresholds in step 5.)<br />
A further lower limit threshold, τexclude, to the SNR may also be applied at this point.<br />
This is useful when deriving spectra <strong>for</strong> adaptive binning from reference samples consisting<br />
<strong>of</strong> a single compound at high concentration. Since all <strong>of</strong> peaks from the sample compound<br />
(rather than contaminants) will have high intensity, this threshold removes all other smaller<br />
peaks. (Although the lower limit thresholds used in step 4 could be used <strong>for</strong> this purpose,<br />
they could remove medium-sized peaks convoluted with the larger sample peaks, making<br />
it harder <strong>for</strong> the GA to fit the sample peaks accurately.)<br />
Optionally, peaks at the F2 <strong>and</strong>/or F1 frequency <strong>of</strong> the solvent used <strong>for</strong> the <strong>NMR</strong> sample<br />
may be excluded on the basis they derive from the solvent rather than the sample itself.<br />
9 - Calculate Peak Volume: For the picked peaks, the volume <strong>of</strong> the peak—the measure<br />
<strong>of</strong> its intensity that takes into account line broadening—is determined by integrating the<br />
intensity over the area <strong>of</strong> the peak. Since the spectrum is a discrete signal, this is calculated<br />
by summing the intensities over the area <strong>of</strong> the peak’s full watershed region determined<br />
in step 5. Although this measurement is not required directly <strong>for</strong> the adaptive binning<br />
technique, it is <strong>of</strong>ten the key datum used when analysing spectra individually.<br />
10 - Derive ‘Clean’ Spectrum: This step prepares the denoised spectrum <strong>for</strong> use in the<br />
adaptive binning analysis by excluding unpicked peaks <strong>and</strong> any remaining t1-noise. For<br />
each peak picked, the full watershed area is exp<strong>and</strong>ed to include points adjacent to the<br />
boundary: these are the points that potentially belong to the watershed <strong>of</strong> more than<br />
one point, equivalent to the bottom <strong>of</strong> valleys in the surface <strong>of</strong> spectrum. This is done<br />
by including points that are a ‘cityblock’ distance <strong>of</strong> 1 grid unit from the watershed (see<br />
section 3.6 where the same technique is used when deriving regions <strong>of</strong> convoluted peaks).<br />
Then any point in the spectrum that is not in the ‘exp<strong>and</strong>ed’ watershed <strong>of</strong> a picked peak<br />
is set to zero intensity.<br />
11 - Save Spectrum: Optionally, the real <strong>and</strong> imaginary parts <strong>of</strong> the resulting spectra may<br />
be saved to files in the <strong>for</strong>mat <strong>of</strong> Bruker Topspin processed data files. (This is usually<br />
done <strong>for</strong> denoised, rather than ‘clean’, spectra in order to evaluate the effectiveness <strong>of</strong> the<br />
denoising algorithm using the Bruker Topspin s<strong>of</strong>tware.)<br />
4.3. Results <strong>and</strong> Discussion. In preparation <strong>for</strong> adaptive binning, the parameters used <strong>for</strong><br />
processing spectra reference samples (consisting <strong>of</strong> a high concentration <strong>of</strong> a single compound) are<br />
chosen to pick only the intense peaks relating to the reference compound itself. For metabolic<br />
sample spectra, the emphasis is different: parameters are chosen to include small intensity peaks<br />
from metabolites at low concentration, while minimising t1-noise <strong>and</strong> other noise artefacts.<br />
In this context, the use <strong>of</strong> the GA <strong>for</strong> peak fitting may be inappropriate since it is unnecessary<br />
<strong>for</strong> reference samples—peaks could be identified by large SNR only—<strong>and</strong> <strong>for</strong> metabolic samples it<br />
does not consistently fit peaks in highly convoluted regions. However, the GA is used in the two<br />
examples below in order to demonstrate the entire process, albeit with a relatively small input to<br />
the peak picking step.<br />
Table 2 gives example parameters <strong>for</strong> deriving the ‘clean’ spectra <strong>for</strong> reference <strong>and</strong> metabolic<br />
samples, incorporating the different emphasis in processing discussed above.<br />
Figure 28(a) shows the resulting clean spectrum <strong>for</strong> a reference sample <strong>of</strong> sucrose; (b) shows the<br />
signals removed in deriving the clean spectrum (as a result <strong>of</strong> both the denoising algorithm <strong>and</strong><br />
48
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Parameter<br />
<strong>Denoising</strong> Algorithm<br />
Reference Sample Metabolic Sample<br />
minimum correlation modulus, R (M)<br />
0.5<br />
maximum number <strong>of</strong> traces, N (M)<br />
3 × data points in minimum F2 peak width<br />
minimum distance from trace, F (M)<br />
1 × minimum F2 peak width<br />
phase-balanced<br />
Peak Identification<br />
yes<br />
minimum SNR compared to thermal noise, τthermal 5 4<br />
minimum SNR compared to t1-noise, τt1<br />
Convoluted Peak Region Identification<br />
5 3<br />
watershed boundary as fraction <strong>of</strong> peak height, θw<br />
Genetic Algorithm<br />
0.1 0.2<br />
number <strong>of</strong> generations 500 500<br />
population size<br />
Peak Picking<br />
40 40<br />
include SNR above, τinclude 40 6<br />
maximum fit metric, Ω 0.001 0.02<br />
exclude t1-noise SNR below, τexclude 20 3<br />
Table 2. Examples <strong>of</strong> parameters <strong>for</strong> deriving ‘clean’ spectra from reference <strong>and</strong><br />
metabolic samples <strong>for</strong> use in adaptive binning.<br />
picking peaks). The parameters used where those in the ‘Reference Sample’ column <strong>of</strong> Table 2.<br />
Figure 29 shows the results from a metabolic sample derived from pea leaves, using the parameters<br />
in the ‘Metabolic Sample’ column <strong>of</strong> the table.<br />
The results indicate that the process described in this section is effective in producing ‘clean’<br />
spectra <strong>for</strong> both metabolic <strong>and</strong> reference samples suitable <strong>for</strong> further analysis by adaptive binning.<br />
In particular, the ‘clean’ spectrum in Figure 28(a) isolates the intense peaks in the reference<br />
sample, while the remainder noise signal in Figure 29(b) shows that the process removes noise but<br />
retains peaks in the metabolic sample: few obviously ‘genuine’ peaks are visible in the remainder<br />
spectrum.<br />
A key part <strong>of</strong> the process is the use <strong>of</strong> the SNR measured against the t1-noise enabling the<br />
peak picking to adapt to the local noise amplitude: in regions with little t1-noise, small intensity<br />
peaks are picked; in regions <strong>of</strong> t1-noise ridges, the threshold is larger (but smaller peaks are<br />
still picked if they are closely fitted to the theoretical peak shape by the GA). This is different<br />
from some traditional peak picking techniques that simply take an absolute intensity threshold<br />
(or, equivalently, an SNR value measured against the same noise signal <strong>for</strong> all the peaks) which<br />
unnecessarily exclude peaks in relatively noise-free regions.<br />
The GA technique <strong>for</strong> fitting metrics, combined with SNR thresholds, is likely to be an effective<br />
peak picking method <strong>for</strong> the st<strong>and</strong>ard analysis (e.g. comparing peak intensities) <strong>of</strong> individual<br />
relatively simple spectra. However, as discussed above, it may not be suitable <strong>for</strong> the processing<br />
<strong>of</strong> samples in preparation <strong>for</strong> adaptive binning where particular considerations <strong>of</strong> reference <strong>and</strong><br />
metabolic samples apply.<br />
49
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
Figure 28. <strong>Spectra</strong> resulting from the denoising <strong>and</strong> peak picking process applied<br />
to an HSQC spectrum <strong>of</strong> sucrose. (Only part <strong>of</strong> the F2 range is shown.) (a)<br />
shows the ‘clean’ spectrum consisting <strong>of</strong> picked peaks only; (b) is the remaining<br />
noise signal.<br />
50
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
Figure 29. <strong>Spectra</strong> resulting from the denoising <strong>and</strong> peak picking process applied<br />
to an HSQC spectrum <strong>of</strong> pea leaf metabolites. (Only part <strong>of</strong> the F2 range<br />
is shown.) (a) shows the ‘clean’ spectrum consisting <strong>of</strong> picked peaks only; (b) is<br />
the remaining noise signal.<br />
51
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
5. Two-Dimensional Adaptive Binning<br />
This section describes the application <strong>of</strong> ‘adaptive binning’ to analyse the composition <strong>of</strong> a<br />
metabolic sample using two-dimensional <strong>NMR</strong> spectra, making use <strong>of</strong> the ‘clean’ (denoised <strong>and</strong><br />
peak-picked) spectra resulting from the process described in the previous section.<br />
5.1. Overview <strong>of</strong> One-Dimensional Adaptive Binning. Direct comparison <strong>of</strong> spectra is not<br />
always possible since the resonant frequency <strong>of</strong> individual peaks can shift owing to factors including<br />
differences in the pH <strong>and</strong> temperature <strong>of</strong> sample. Binning groups the data into equal-sized ‘bins’<br />
or ‘buckets’ so that a specific peaks falls within the same bin at all observed shifts. However,<br />
binning takes no account <strong>of</strong> the actual distribution <strong>of</strong> the peaks in spectra <strong>and</strong> this can limit the<br />
ability to resolve subtle differences in spectra. Adaptive Binning, described in [6] in the context<br />
<strong>of</strong> one-dimensional 1 H <strong>NMR</strong> spectra <strong>of</strong> metabolic samples, overcomes some <strong>of</strong> the limitations <strong>of</strong><br />
binning.<br />
The starting point is a set <strong>of</strong> spectra derived from equivalent metabolic samples. The spectra<br />
are combined by taking the maximum intensity at each frequency across the entire set <strong>of</strong> spectra.<br />
The resulting ‘combined’ spectrum has maxima at frequencies matching a peak in one <strong>of</strong> more <strong>of</strong><br />
the original spectra.<br />
However, peaks from the same compound that have shifted more than the resolution <strong>of</strong> the <strong>NMR</strong><br />
experiment, owing to pH or temperature differences, will appear as separate, but closely grouped<br />
peaks in the combined spectrum. The combined spectrum is smoothed, using non-decimating<br />
wavelet smoothing, to merge these peaks into a single peak. The level <strong>of</strong> wavelet decomposition<br />
to effect suitable smoothing is dependent on the width <strong>of</strong> the peaks <strong>and</strong> the degree <strong>of</strong> shift in the<br />
samples.<br />
Boundaries <strong>of</strong> bins are identified in the smoothed spectrum by locating the local intensity<br />
minima. The process is termed ‘adaptive’ in that the resulting bin size changes according to the<br />
local shape <strong>of</strong> the spectrum instead <strong>of</strong> being a fixed size.<br />
Once the bins have been identified, the intensity <strong>of</strong> each sample spectrum is integrated within<br />
each bin to give a series <strong>of</strong> data points <strong>for</strong> each spectrum. The data points may then be evaluated<br />
using multivariate data analysis methods, such as principal component analysis[6], or natural<br />
computational techniques such as genetic programming[7].<br />
5.2. Objective <strong>for</strong> Two-Dimensional Adaptive Binning Research. The purpose <strong>of</strong> the<br />
research on adaptive binning described here was to evaluate methods <strong>of</strong> implementing the technique<br />
in <strong>2D</strong> <strong>NMR</strong> spectra. Given the time taken to acquire detailed <strong>2D</strong> <strong>NMR</strong> spectra, creating a large<br />
set <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> from equivalent metabolic samples was not feasible. Instead, a modified objective<br />
was designed to test the method: to compare a metabolic sample against spectra <strong>of</strong> a reference<br />
compound in order to assess the presence <strong>of</strong> the reference compound in the metabolome.<br />
5.3. Two-Dimensional Adaptive Binning Method.<br />
5.3.1. Sample <strong>and</strong> Reference <strong>Spectra</strong>. The data used were a <strong>2D</strong> HSQC spectra from metabolomic<br />
sample derived from pea leaves, <strong>and</strong> a set <strong>of</strong> reference spectra <strong>of</strong> sucrose at different pHs. For<br />
ease <strong>of</strong> comparison, all the spectra were measured using equivalent acquisition <strong>and</strong> processing<br />
parameters.<br />
The spectra were firstly ‘cleaned’ to remove t1-noise <strong>and</strong> other noise artefacts as described<br />
in section 4. The processing parameters <strong>of</strong> the metabolomic sample was chosen to retain small<br />
intensity peaks, while <strong>for</strong> the reference sample, the processing removed all but the high intensity<br />
peaks relating to the reference compound itself. The parameters <strong>and</strong> processing are those described<br />
in section 4.3 <strong>and</strong> Table 2, except that the SNR thresholds <strong>for</strong> the reference spectra were multiplied<br />
by a factor <strong>of</strong> 10 since these spectra were acquired using gradient-selected HSQC which introduces<br />
less noise.<br />
5.3.2. ‘Combined’ Spectrum. Denoting the <strong>2D</strong> metabolomic spectrum as Φ 0 , <strong>and</strong> the N reference<br />
spectra as Φ i , where i = 1, ..., N, the ‘combined’ spectrum is derived by taking the maximum<br />
52
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
intensity at each discrete frequency point in the two dimensions, i.e.:<br />
Φ(f1, f2) = max Φ 0 (f1, f2), Φ 1 (f1, f2), Φ 2 (f1, f2), . . .,Φ N (f1, f2) <br />
where Φ(f1, f2) is the combined spectrum.<br />
Figure 30(a) shows a small region <strong>of</strong> a combined spectrum. The combined spectrum was derived<br />
using two reference spectra at different pHs. In each <strong>of</strong> the two reference spectra shown in (b) <strong>and</strong><br />
(c), two major peaks can be seen in this region, with peaks in one spectrum visibly shifted with<br />
respect to the other in the F2 ( 1 H) direction. In the combined spectrum, the peaks give rise to<br />
two sets <strong>of</strong> adjacent intense peaks.<br />
5.3.3. Smoothed Spectrum. The smooth spectrum is derived using the wavelet smoothing, applied<br />
to the <strong>2D</strong> spectra <strong>and</strong> using the non-decimating trans<strong>for</strong>m. (See sections B.7.3, B.8 <strong>and</strong> B.9.)<br />
The wavelet chosen <strong>for</strong> smoothing was the Haar wavelet (section B.6.2) since this wavelet is<br />
potentially faster to process than other wavelets given its simple <strong>for</strong>m. Per<strong>for</strong>mance was an important<br />
factor since the non-decimating trans<strong>for</strong>m to level m requires 2 2m separate applications<br />
<strong>of</strong> the <strong>2D</strong> pyramid algorithm (section B.9). Since the non-decimating trans<strong>for</strong>m tends to average<br />
out artefacts resulting from poor approximation <strong>of</strong> the signal by the wavelet shape[20], the<br />
discontinuous shape <strong>of</strong> the Haar wavelet is not as important.<br />
It was found, by experiment, that using wavelet decomposition to level 3 gave the best results in<br />
merging shifted peaks into a single peak while still retaining separate regions <strong>for</strong> unrelated peaks.<br />
The decomposition level will depend on the peak width (related to the resolution <strong>of</strong> the <strong>NMR</strong><br />
experiment), <strong>and</strong> the degree <strong>of</strong> shift in each reference sample.<br />
Figure 31 shows smoothed spectrum <strong>for</strong> the same region that was shown in Figure 30. It can<br />
be seen that the smoothing has merged the two sets <strong>of</strong> shifted peaks into two distinct peaks.<br />
5.3.4. Bin Derivation. In the 1D context, bins are identified from the smoothed spectrum by<br />
locating the minima either side <strong>of</strong> a peak: the minima are the ends <strong>of</strong> the bin. In the <strong>2D</strong> case,<br />
an equivalent process is to derive the watershed <strong>of</strong> the peaks in the smoothed spectrum, <strong>and</strong> the<br />
bin is then the area covered by the watershed. (The derivation <strong>of</strong> watersheds is discussed in more<br />
detail in section 3.6.)<br />
If the adaptive binning process were being used <strong>for</strong> locating distinguishing markers in a set <strong>of</strong><br />
<strong>2D</strong> metabolomic spectra, all the watersheds (<strong>for</strong> peaks above a given intensity threshold) would<br />
be considered as bins. In this example <strong>of</strong> identifying a reference compound in a metabolic sample,<br />
only the bins associated with the reference compound are relevant. The condition used is to only<br />
consider a bin/watershed if a peak from one or more <strong>of</strong> the original ‘clean’ reference spectra is<br />
located in the watershed.<br />
Figure 32 shows the watershed bins derived from the pea leaf metabolic spectrum with two<br />
sucrose reference spectra. The peaks shown in Figures 30 <strong>and</strong> 31 result in bins numbered 8 <strong>and</strong><br />
10.<br />
5.3.5. Intensity Comparison. To compare samples, the intensity <strong>of</strong> the metabolic spectrum is<br />
integrated over each <strong>of</strong> the watershed bin regions. The same is per<strong>for</strong>med <strong>for</strong> one (or more) <strong>of</strong><br />
the reference spectra. The ratio <strong>of</strong> the integrated intensities (equivalent to the ‘volume’ <strong>of</strong> peaks<br />
in the bin) <strong>for</strong> each bin is a measure <strong>of</strong> the concentration <strong>of</strong> the compound in metabolite sample<br />
compared to the reference sample (assuming equivalent experiments in each case). It is an upper<br />
limit on the concentration since nearby peaks from other compounds in the metabolic spectrum<br />
may have been included in the bin.<br />
5.4. Results <strong>and</strong> Discussion. Table 3 shows the integrated intensities over each <strong>of</strong> the bins <strong>for</strong><br />
the pea spectrum <strong>and</strong> the two reference sucrose spectra. A direct comparison <strong>of</strong> concentration<br />
<strong>of</strong> sucrose in the metabolic <strong>and</strong> reference samples cannot be made in this case since different<br />
experimental techniques were used (phase-cycled <strong>and</strong> gradient-selected respectively). The ratios<br />
<strong>of</strong> integrated intensities (the fourth column in the table) range from 1.7% to 6.6%; ideally a more<br />
consistent ratio would be expected, although other nearby peaks, not related to sucrose, in the<br />
metabolic spectrum may have increased some ratios. Nevertheless, a qualitative interpretation is<br />
53<br />
(5.1)
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
(c)<br />
Intensity<br />
Intensity<br />
Intensity<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
−1<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
−1<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
−1<br />
x 10 7<br />
3.6<br />
x 10 7<br />
3.6<br />
x 10 7<br />
3.6<br />
3.55<br />
3.5<br />
3.5<br />
3.5<br />
3.45<br />
F 2 ( 1 H) / ppm<br />
3.4<br />
F 2 ( 1 H) / ppm<br />
3.4<br />
F 2 ( 1 H) / ppm<br />
3.4<br />
3.35<br />
3.3<br />
3.3<br />
72<br />
72<br />
72<br />
70<br />
70<br />
70<br />
68<br />
F 1 ( 13 C) / ppm<br />
68<br />
F 1 ( 13 C) / ppm<br />
68<br />
F 1 ( 13 C) / ppm<br />
Figure 30. (a) shows a small region <strong>of</strong> the combined spectrum from a metabolic<br />
sample (derived from pea leaves) <strong>and</strong> two sucrose reference samples. The reference<br />
samples, shown in (b) <strong>and</strong> (c), were a neutral <strong>and</strong> acidic pH respectively. (The<br />
orientation <strong>of</strong> the axes is non-st<strong>and</strong>ard in order to clarify the view <strong>of</strong> the peaks.)<br />
54
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Intensity<br />
3<br />
2.5<br />
2<br />
1.5<br />
1<br />
0.5<br />
0<br />
x 10 7<br />
3.6<br />
3.55<br />
3.5<br />
3.45<br />
F 2 ( 1 H) / ppm<br />
3.4<br />
3.35<br />
72<br />
70<br />
68<br />
F 1 ( 13 C) / ppm<br />
Figure 31. A small region <strong>of</strong> the smoothed spectrum derived from spectra <strong>of</strong> a<br />
metabolic sample <strong>and</strong> two sucrose reference samples.<br />
Figure 32. The watershed ‘bins’ identified in the smoothed spectrum from a pea<br />
leaf metabolic sample <strong>and</strong> two sucrose reference sample. Bin have been assigned<br />
numbers to assist identification. (Only the part <strong>of</strong> the spectrum containing the<br />
bins is shown.)<br />
that the presence <strong>of</strong> significant intensity in each <strong>of</strong> the ten bins suggests the presence <strong>of</strong> sucrose<br />
in the metabolic sample.<br />
The last column <strong>of</strong> Table 3 is the ratio <strong>of</strong> integrated intensities <strong>for</strong> the two reference samples.<br />
It is used here as a check on the adaptive binning technique: the ratios would be expected to be<br />
consistent if the technique correctly identified bins that accounted <strong>for</strong> the shift in peaks owing<br />
to sample pH <strong>and</strong> temperature. While the ratios are significantly more consistent than between<br />
the metabolite <strong>and</strong> reference spectra, there is still some variation, with the ratios varying between<br />
75.3% to 90.5%. This suggests further investigation <strong>of</strong> the parameters to the adaptive binning<br />
process—such as the level <strong>of</strong> wavelet decomposition <strong>for</strong> smoothing or whether to truncate watersheds<br />
at a certain proportion <strong>of</strong> the peak height (described in section 3.6)—is required to produce<br />
more consistent ratios between the reference spectra.<br />
It should also be noted that this test <strong>of</strong> the process used only two reference samples. Normally,<br />
a larger set <strong>of</strong> reference spectra with different peak shifts would be used. Since the peaks in<br />
additional spectra would be located between the shifted peaks in the neutral <strong>and</strong> acidic sucrose<br />
55
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Intensity Integrated over Bin / 10 8 units Ratio <strong>of</strong> Ratio <strong>of</strong><br />
Bin Sucrose Sucrose Pea Pea to Sucrose (Acidic) to<br />
(Neutral) (Acidic) Metabolites Sucrose (Neutral) Sucrose (Neutral)<br />
1 40.14 31.82 1.432 3.57% 79.3%<br />
2 33.03 26.58 2.186 6.62% 80.5%<br />
3 35.77 26.92 2.019 5.65% 75.3%<br />
4 29.25 26.29 0.534 1.83% 89.9%<br />
5 26.60 22.15 0.711 2.67% 83.3%<br />
6 48.91 41.06 1.232 2.52% 83.9%<br />
7 23.43 21.02 0.401 1.71% 89.7%<br />
8 22.15 18.50 1.242 5.61% 83.5%<br />
9 24.01 21.07 0.773 3.22% 87.8%<br />
10 21.69 19.63 0.846 3.90% 90.5%<br />
Table 3. The integrated intensity over each bin <strong>for</strong> the metabolic spectrum <strong>and</strong><br />
two reference spectra <strong>of</strong> sucrose, <strong>and</strong> the intensity ratios between spectra. The<br />
bin numbers are those assigned in Figure 32.<br />
‘Unprocessed’ Pea Intensity Ratio to<br />
Bin Integrated over Bin / 10 8 units Sucrose (Neutral)<br />
1 1.967 4.90%<br />
2 2.212 6.70%<br />
3 2.562 7.16%<br />
4 0.513 1.75%<br />
5 0.785 2.95%<br />
6 1.895 3.87%<br />
7 0.728 3.11%<br />
8 1.332 6.01%<br />
9 0.852 3.55%<br />
10 0.911 4.20%<br />
Table 4. The integrated intensity over each bin <strong>for</strong> the unprocessed (without<br />
denoising <strong>and</strong> peak picking) metabolic spectrum, <strong>and</strong> the ratio to the (processed)<br />
neutral sucrose spectrum.<br />
spectra used above, a smaller level <strong>of</strong> smoothing might be possible when identifying bins that<br />
group together the shifted peaks. In general, smoothing to a smaller decomposition level is likely<br />
to result in more accurately defined bins (as increased smoothing tends to broaden the shape<br />
<strong>of</strong> smoothed peaks), <strong>and</strong> this in turn might result in more accurate results when intensities are<br />
compared between bins.<br />
Finally, Table 4 shows similar calculations using the spectrum <strong>of</strong> the metabolic pea sample<br />
without any denoising <strong>and</strong> peak picking. The integrated intensities show values that are generally<br />
larger when compared to the equivalent bins <strong>for</strong> the processed ‘clean’ pea spectrum given in<br />
Table 3. Although the decrease in intensities in the processed spectrum is suggestive <strong>of</strong> the effect<br />
that motivated the use <strong>of</strong> phase-balanced masking criteria (section 2.6.2), it may also be caused by<br />
the general decrease in t1-noise included in the bins: further investigation is required to establish<br />
the reason. The range <strong>of</strong> ratios is slightly larger <strong>for</strong> the unprocessed spectrum at 1.7% to 7.2%,<br />
although no inference can be made given this limited data set. However, the broadly similar<br />
results do indicate that, <strong>for</strong> this case at least, the processing <strong>of</strong> the spectrum to remove t1-noise<br />
<strong>and</strong> peak picks has not introduced significant artefacts nor completely removed small peaks in the<br />
metabolic spectrum.<br />
56
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
6. Conclusion<br />
6.1. Evaluation <strong>of</strong> Project Objectives. Considering each <strong>of</strong> the objectives defined in the introduction:<br />
Reduction <strong>of</strong> t1-Noise: The denoising algorithm described in section 2.6 is shown to be<br />
effective at reducing t1-noise in phase-cycled HSQC spectra, while retaining small ‘genuine’<br />
peaks convoluted with t1-noise ridges. In the sucrose/glycine spectra analysed in<br />
section 2.7, the algorithm reduced the t1-noise by a factor ranging between 2 <strong>and</strong> 4 depending<br />
on the F2 location across the ridge, <strong>and</strong> thereby improved the signal-to-noise ratio<br />
<strong>of</strong> small peaks convoluted with the noise by a similar factor. The algorithm showed similar<br />
improvements in metabolic spectra, with the proviso that, under particular circumstances,<br />
it can significantly reduce the intensity <strong>of</strong> small genuine peaks within t1-noise ridges. Although<br />
a quantitative comparison was not made, the algorithm appears to have advantages<br />
over existing t1-noise reduction methods, such as reference deconvolution (section 2.8).<br />
Automated Peak Picking: Section 3 describes a peak-fitting genetic algorithm (GA) that<br />
incorporated some <strong>of</strong> the knowledge used by experimenters during manual peak picking.<br />
Section 4 evaluated the use <strong>of</strong> the GA in conjunction with both the denoising algorithm<br />
<strong>and</strong> a SNR-based peak picking method that took account <strong>of</strong> the variation in t1-noise.<br />
The GA was able to distinguish between genuine peaks <strong>and</strong> noise artefacts, particularly<br />
well in case <strong>of</strong> simple spectra (section 3.9). For metabolic spectra, regions consisting <strong>of</strong> a<br />
large number <strong>of</strong> highly convoluted peaks were not consistently resolved by the GA within<br />
a practicable number <strong>of</strong> generations. This was improved to some extent by modifying<br />
parameters to reduce the number <strong>of</strong> peaks in each convoluted region, <strong>and</strong> by using SNRbased<br />
thresholding to identify the largest peaks. The hybrid process was suitable <strong>for</strong><br />
producing spectra free <strong>of</strong> noise artefacts <strong>for</strong> use in adaptive binning, <strong>for</strong> both reference<br />
<strong>and</strong> metabolic spectra.<br />
Two-Dimensional Adaptive Binning: The test <strong>of</strong> adaptive binning was to compare a<br />
metabolic spectrum with reference spectra <strong>of</strong> a single compound. Section 5 proposed<br />
(a) the use <strong>of</strong> <strong>2D</strong> non-decimating wavelet smoothing, <strong>and</strong>, (b) the use <strong>of</strong> watershed regions<br />
to define bins, as two-dimensional equivalents <strong>of</strong> the corresponding methods in one<br />
dimension. The technique proved effective <strong>for</strong> identifying the presence <strong>of</strong> sucrose in a<br />
metabolic pea sample, although the results suggests that the parameter choices may not<br />
be optimal. Evaluation with larger number <strong>of</strong> reference spectra, or directly comparing a<br />
number <strong>of</strong> metabolic spectra, is necessary to improve the adaptive binning technique in<br />
two dimensions.<br />
6.2. Further Investigation. A number <strong>of</strong> possibilities <strong>for</strong> further investigation were identified:<br />
• Section 2.7.1 describes an alternative derivation <strong>of</strong> the noise ‘masking’ spectrum by considering<br />
the correlation independently at each level <strong>of</strong> the wavelet decomposition <strong>of</strong> F2<br />
traces. The resulting reduction in t1-noise was similar to the st<strong>and</strong>ard algorithm, <strong>and</strong> <strong>for</strong><br />
some ridges slightly better. However, it tended to be less consistent, occasionally resulting<br />
in significantly less noise reduction at certain points in the spectrum. It is possible that<br />
further investigation <strong>of</strong> optimum parameters <strong>for</strong> the wavelet-level mask derivation might<br />
result in a method that reduces noise more than the st<strong>and</strong>ard algorithm <strong>and</strong> is similarly<br />
consistent.<br />
• It may also be possible to separate the noise from small genuine peaks using a different<br />
method. If each F2 trace in the noise spectrum were both normalised in amplitude <strong>and</strong><br />
phase adjusted (using the argument <strong>of</strong> its complex correlation to a chosen reference trace),<br />
the resulting ‘phase-corrected’ surface might show only large scale variation in the noise<br />
across F2 directions while small ‘genuine’ peaks in the noise spectrum would be small scale<br />
features. These could be separated using wavelet analysis (applied to the F2 direction),<br />
discarding the large scale noise while retaining small scale peaks. After reversing the<br />
normalisation <strong>and</strong> phase adjustment, the resulting small peak spectrum would be added<br />
back to the peak spectrum originally separated from the noise.<br />
57
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
• A limitation <strong>of</strong> the GA was that regions consisting <strong>of</strong> a number <strong>of</strong> convoluted peak could<br />
not be consistently fitted to the required degree <strong>of</strong> accuracy within a reasonable number <strong>of</strong><br />
generations. Section 3.9 suggests an alternative technique: instead <strong>of</strong> fitting all peaks in<br />
a region simultaneously, the largest peaks are fitted first moving progressively to smaller<br />
peaks. By fitting only one peak at a time (while still considering the entire region), this<br />
alternative method may be able to accurately fit the region in a reasonable time.<br />
• Section 2.5.6 suggests how the change in the phase angle <strong>of</strong> the noise with F2 might be<br />
used to implement higher order phase correction <strong>of</strong> the entire spectrum.<br />
58
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Appendix A. Pulse Fourier Trans<strong>for</strong>m <strong>NMR</strong><br />
Nuclear Magnetic Resonance (<strong>NMR</strong>) is a spectroscopic technique that provides in<strong>for</strong>mation<br />
on the structure <strong>of</strong> chemical compounds using the magnetic properties <strong>of</strong> atomic nuclei. This<br />
appendix describes the theory <strong>and</strong> method <strong>of</strong> Pulse Fourier Trans<strong>for</strong>m (FT) <strong>NMR</strong> which is the<br />
technique used in modern <strong>NMR</strong> spectrometers.<br />
A.1. Nuclear Magnetic Moment.<br />
A.1.1. Magnetic Nuclei. Atomic nuclei possess a vector property known as spin angular momentum,<br />
denoted here by L. Nuclei where the spin is non-zero are termed magnetic nuclei since the<br />
the non-zero spin angular momentum gives rise to a magnetic moment, µ. The ratio between<br />
these two vector properties is the gyromagnetic ratio, γ:<br />
γ is the same <strong>for</strong> all nuclei <strong>of</strong> an isotope, but differs between isotopes.<br />
µ = γL (A.1)<br />
A.1.2. Spin Quantum Number <strong>and</strong> Magnetic Quantum Number. The spin, L, <strong>of</strong> an individual<br />
nucleus is a quantised according to another property <strong>of</strong> the nucleus, the spin quantum number, I.<br />
The nuclei considered in this project, 1H <strong>and</strong> 13C, have I = 1<br />
2 <strong>and</strong> are referred to as spin-1 2 nuclei.<br />
The quantisation restricts the magnitude <strong>of</strong> the spin vector to the value:<br />
L = I(I + 1) (A.2)<br />
(where = h/2π <strong>and</strong> h is Planck’s constant), while the component <strong>of</strong> L along an arbitrary axis,<br />
say the z axis, may take only values:<br />
Lz = m (A.3)<br />
where m, the magnetic quantum number, takes the values:<br />
m = −I, −I + 1, −I + 2, . . . , I − 2, I − 1, I (A.4)<br />
A.1.3. Quantisation in a Magnetic Field. If the nucleus is in an external magnetic field, B0, there<br />
is an energy associated with the magnetic moment given by:<br />
E = −µ · B0<br />
(A.5)<br />
In addition, the quantisation axis <strong>for</strong> the spin, <strong>and</strong> thus <strong>for</strong> the magnetic moment, is the direction<br />
<strong>of</strong> B0. Taking the direction <strong>of</strong> B0 to be the positive z axis, then from (A.1) <strong>and</strong> (A.3):<br />
Using this in (A.5) gives,<br />
µz = γLz<br />
= mγ (A.6)<br />
E = −µzB0<br />
= −mγB0<br />
(A.7)<br />
A.1.4. Resultant Energy Levels. Since the magnetic quantum number, m, takes the values detailed<br />
in (A.4) which differ by 1, the interaction <strong>of</strong> the magnetic moment <strong>and</strong> external magnetic field<br />
gives rise to a set <strong>of</strong> energy levels that differ by ∆E = γB0. Assuming thermal equilibrium,<br />
nuclei will populate these energy levels according to the Boltzmann distribution. For example, <strong>for</strong><br />
spin-1 1<br />
2 nuclei, there will more nuclei at the lower energy level (m = 2 , assuming a positive value<br />
<strong>of</strong> γ) than the higher level (m = −1 2 ).9<br />
9 Even with the strong magnetic fields used in modern <strong>NMR</strong> spectrometers, the difference in energy levels is<br />
small compared to the room temperature, so the excess nuclei at the lowest energy level is only a small proportion<br />
<strong>of</strong> the total number <strong>of</strong> nuclei[14].<br />
59
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
A.1.5. Resonance Frequency. The difference between energy levels relates directly to the resonance<br />
frequency ν <strong>of</strong> the nucleus using the relation:<br />
giving:<br />
∆E = hν (A.8)<br />
ν = ∆E<br />
h<br />
= γB0<br />
h<br />
= γB0<br />
2π<br />
(A.9)<br />
A.2. Pulse <strong>NMR</strong>. The pulse technique used in modern <strong>NMR</strong> spectrometers can be described by<br />
considering the bulk magnetisation <strong>of</strong> the nuclei in the sample. For this description, it is possible to<br />
use the classical physics <strong>of</strong> magnetic moments rather than the quantum mechanics used above[9].<br />
A.2.1. Net Magnetic Moment. The sample, in solution, is placed in a strong, static, homogeneous<br />
magnetic field <strong>of</strong> the <strong>for</strong>m described above. The slightly higher number <strong>of</strong> nuclei at lower energy<br />
levels described above gives rise to a net magnetization in the z direction; if γ is positive then the<br />
direction is in the same direction as the external magnetic field, along the positive z axis. Owing<br />
to the quantisation <strong>of</strong> the magnitude <strong>of</strong> the spin angular moment given by (A.2), <strong>and</strong> in turn the<br />
nuclear magnetic moment, each nucleus has some component <strong>of</strong> its magnetic moment in the x-y<br />
plane in addition to the component quantised along the z axis. However, in the external magnetic<br />
field acting in the z direction, there is no preferred direction <strong>for</strong> these components in the x-y plane<br />
<strong>and</strong> so there is no net magnetic moment in this plane. Thus (<strong>and</strong> again assuming a positive γ), the<br />
net magnetic moment <strong>of</strong> the nuclei in the sample can be considered to be a vector in the positive<br />
z direction, in the same direction as the external magnetic field B0.<br />
A.2.2. Effect <strong>of</strong> Radio Frequency Pulse. A magnetic field, B1, is applied perpendicular to the<br />
static B0 field using a short radio frequency (RF) pulse in a coil that surrounds the sample. The<br />
magnetic field created by the pulse pulse is very much weaker than B0, <strong>and</strong> oscillates at the<br />
resonance frequency <strong>of</strong> the nuclei being observed. 10<br />
It is convenient at this point to consider a coordinate system rotating about the z axis at the<br />
same frequency as the pulse. The axes in this rotating frame will be denoted x ′ , y ′ <strong>and</strong> z ′ . In this<br />
new coordinate system, the RF magnetic field, B1 is static, <strong>and</strong>, without loss <strong>of</strong> generality, it is<br />
taken that the direction lies along the positive x ′ axis.<br />
The interaction <strong>of</strong> the net magnetic moment <strong>and</strong> the overall magnetic field creates a torque.<br />
The effect on the (spin) angular momentum is given by:<br />
dΛ<br />
dt<br />
= M × B (A.10)<br />
where Λ denotes the net angular momentum, <strong>and</strong> M the net magnetic moment, <strong>and</strong> B the overall<br />
magnetic field.<br />
Since M = γΛ by extension <strong>of</strong> (A.1),<br />
dM<br />
dt<br />
= γM × B (A.11)<br />
When considered in a rotating frame at angular velocity <strong>of</strong> ω, this becomes[9]:<br />
∂M<br />
∂t<br />
= M × (γB − ω) (A.12)<br />
10 As described below, the nuclei being observed will have a range <strong>of</strong> the resonance frequencies, but if the<br />
difference from the frequency <strong>of</strong> the RF field is small compared to γB1, the effect <strong>of</strong> the pulse, as described below,<br />
remains a good approximation[9].<br />
60
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a) (b)<br />
(c) (d)<br />
Figure 33. The orientation <strong>of</strong> the bulk magnetic moment, M, <strong>and</strong> the effective<br />
magnetic field B (a) at the start <strong>of</strong> the RF pulse; (b) at the end <strong>of</strong> the pulse;<br />
(c) precessing after the pulse; <strong>and</strong> (d) during relaxation. Note that (a) <strong>and</strong> (b)<br />
show the frame rotating with the RF pulse, while (c) <strong>and</strong> (d) show the stationary<br />
laboratory frame.<br />
In the case <strong>of</strong> the frame rotating at the resonance frequency, ω = 2πνiz = γB0 from (A.9),<br />
where iz is a unit vector in the positive z direction. During the pulse, the overall magnetic field<br />
is B0 + B1, giving:<br />
∂M<br />
∂t = M × {γ(B0 + B1) − γB0}<br />
= γM × B1<br />
(A.13)<br />
Thus, when considered in the rotating frame, the net magnetic moment is subject to a torque<br />
that rotates it around the direction <strong>of</strong> the RF magnetic field. Since the RF magnetic field is<br />
static along the x ′ axis in the rotating frame, the net magnetic moment rotates around x ′ (in an<br />
clockwise direction assuming positive γ) in the y ′ -z ′ plane: see Figure 33(a). The duration <strong>of</strong> the<br />
RF magnetic field pulse is timed so that at the end <strong>of</strong> the pulse, the net magnetic moment lies<br />
along the positive y ′ -axis, i.e. a clockwise rotation <strong>of</strong> π/2 (Figure 33(b)).<br />
A.2.3. Precession After RF Pulse. After the pulse, the overall magnetic field is just B0, so returning<br />
to equation (A.12),<br />
∂M<br />
∂t = M × (γB0 − γB0)<br />
= 0 (A.14)<br />
Thus the net magnetic moment is stationary in the rotating frame. In the static frame, this means<br />
the net magnetic moment must be rotating, or precessing, around B0 at the same angular velocity<br />
61
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
as the rotating frame (Figure 33(c)). This angular velocity is ω = γB0, <strong>and</strong> there<strong>for</strong>e the moment<br />
precesses at a frequency <strong>of</strong>:<br />
ν = ω<br />
2π<br />
= γB0<br />
(A.15)<br />
2π<br />
This frequency is identical to the resonance frequency given by the quantum mechanical description<br />
<strong>of</strong> a transition between energy levels <strong>of</strong> an individual nucleus (A.9). The rotating magnetic<br />
moment gives rise to an oscillating voltage in a receiver coil around the sample, <strong>and</strong> it is this<br />
voltage that is detected <strong>and</strong> processed by the <strong>NMR</strong> spectrometer.<br />
A.3. Relaxation. After the RF frequency pulse, the net magnetic moment gradually returns to<br />
the equilibrium position <strong>of</strong> alignment along the positive z axis, a process known as relaxation<br />
(Figure 33(d)).<br />
A.3.1. Longitudinal Relaxation. There are two separate processes that give rise to this relaxation.<br />
Firstly, the component <strong>of</strong> the net magnetic moment along the z axis, Mz following the notation<br />
used above, returns to its equilibrium value. This is called longitudinal or spin-lattice relaxation.<br />
In a classical description, this may be viewed as a induced magnetic field occurring in the sample<br />
as a result <strong>of</strong> the external magnetic field, B0, where the sample is unmagnetised in the z direction<br />
immediately after the pulse [9]. In the quantum mechanical description, it may be viewed as<br />
the population at each <strong>of</strong> the energy levels returning to the Boltzmann distribution at thermal<br />
equilibrium. It is assumed [9] that the return to the equilibrium state occurs exponentially, such<br />
that:<br />
Mz(t) = Mz(1 − e −t/T1 ) (A.16)<br />
where Mz is the equilibrium value. The value <strong>of</strong> T1, the spin-lattice relaxation time, <strong>and</strong> is<br />
dependent on the nature <strong>of</strong> the sample as well as other factors.<br />
A.3.2. Transverse Relaxation. Correspondingly, the component <strong>of</strong> the net magnetic moment in<br />
the x-y plane decreases over time, at least as fast as the magnetic moment in the z direction<br />
returns. A second process contributes to the reduction in the x-y component. It arises from<br />
inhomogeneity in the static magnetic field, B0: small differences across the sample means that<br />
the magnetic moments <strong>of</strong> individual nuclei precess over a small range <strong>of</strong> angular velocities, rather<br />
than the single velocity related to the resonance frequency. Over time, the difference in velocities<br />
means that the magnetic moments ‘fan out’ <strong>and</strong> begin to cancel each other, leading to a reduction<br />
in the net magnetic moment in the x-y plane. This process is called called transverse relaxation.<br />
The total relaxation—the combination <strong>of</strong> both transverse <strong>and</strong> longitudinal processes—in the x-y<br />
plane is also assumed to decay to zero exponentially with a parameter denoted as T2 [9].<br />
A.4. Chemical Shift. While all nuclei <strong>of</strong> a particular isotope have the same gyromagnetic constant,<br />
their resonance frequencies will differ depending on the chemical environment <strong>of</strong> each nucleus.<br />
Neighbouring nuclei can either increase or decrease the actual magnetic field experienced<br />
by nucleus through their action on the electrons <strong>of</strong> the atom in question, leading to a change in<br />
the resonance frequency called chemical shift. The actual magnetic field experience by the nucleus<br />
is denoted as B0(1 −σ) where σ is a screening constant. 11 This leads to a change in the resonance<br />
frequency so that now:<br />
ν = γB0(1 − σ)<br />
(A.17)<br />
The chemical shift is the key datum arising from typical <strong>NMR</strong> experiments since it provides<br />
in<strong>for</strong>mation about the molecular structure near specific nuclei.<br />
11 Nuclei that are not part <strong>of</strong> molecule will also experience shielding caused by the electrons within the atom<br />
itself <strong>and</strong> this effect is also measured by the shielding constant[14].<br />
62<br />
2π
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
The chemical shift is normally expressed by comparison with the resonance frequency <strong>of</strong> the<br />
same isotope in a reference compound, νref. The difference between the frequencies is expressed<br />
in parts per million, denoted ppm, so the value is calculated as:<br />
δ = 10<br />
6ν − νref<br />
νref<br />
(A.18)<br />
A.5. Spin-Spin Coupling. Neighbouring nuclei can also act directly on the resonance frequency<br />
<strong>of</strong> a nucleus, as opposed to chemical shifts which result from indirect action on the electrons. If a<br />
nucleus, say A, has a neighbouring nucleus, X, which is magnetic (has a non-zero spin), then the<br />
magnetic moment <strong>of</strong> X will cause a small magnetic field at A that will either enhance or oppose<br />
the external magnetic field depending on the direction <strong>of</strong> the magnetic moment <strong>of</strong> X.<br />
The energy associated with the spin-spin coupling is quantified by the spin-spin coupling constant<br />
between A <strong>and</strong> X, JAX [9]:<br />
E = hJAXmAmX<br />
(A.19)<br />
where mA <strong>and</strong> mX are the quantum magnetic numbers <strong>for</strong> A <strong>and</strong> X respectively. When considering<br />
changes in the resonance frequency <strong>of</strong> A, ∆νA (i.e. <strong>for</strong> energy level transitions where ∆mA = 1),<br />
then (A.8) <strong>and</strong> (A.19) give:<br />
∆νA = JAXmX<br />
(A.20)<br />
For example, if X is a spin-1 2 nucleus, <strong>for</strong> which mX has two values: 1<br />
2 or −1<br />
2 , approximately<br />
half the X nuclei in the sample will have m = 1<br />
2 , the other half having m = −1<br />
2 , leading to a<br />
doublet: two resonance frequency lines <strong>of</strong> equal intensity symmetrically arranged above <strong>and</strong> below<br />
the resonance frequency <strong>of</strong> A if spin-spin coupling had not occurred. Since the spacing between<br />
possible values <strong>of</strong> mX is 1, the frequency difference between the doublet lines is JAX.<br />
If A has spin coupling with N neighbouring nuclei, then (A.20) becomes [9]:<br />
N<br />
∆νA =<br />
(A.21)<br />
k=1<br />
JAXk mXk<br />
If all the Xk are ‘equivalent’ nuclei—specifically, when JAXk is the same <strong>for</strong> all k <strong>and</strong> each<br />
mXk takes the same set <strong>of</strong> possible values—then by considering the number <strong>of</strong> combinations<br />
<strong>of</strong> (mX1, mX2, . . . , mXN) giving the same total <strong>for</strong> N mXk k=1 , it can be seen that the ratio <strong>of</strong><br />
intensities <strong>of</strong> the frequencies in the multiplet are binomial coefficients. For example, a triplet will<br />
have ratios 1:2:1 <strong>and</strong> a quartet will be 1:3:3:1. If the Xk refer to nuclei that are not equivalent,<br />
then more complex multiplet patterns can occur.<br />
A.6. Signal Detection <strong>and</strong> Processing.<br />
A.6.1. Detection. The signal in the receiver coil, induced by the rotating net magnetic moment <strong>of</strong><br />
nuclei in the sample as described above, is proportional to the rate <strong>of</strong> change <strong>of</strong> magnetisation, so<br />
immediately after the pulse, the x component <strong>of</strong> the received signal is at a maximum <strong>and</strong> then is<br />
sinusoidal with a period equal to the resonance frequency. This is termed the absorption signal[9].<br />
The y component is π/2 out <strong>of</strong> phase <strong>and</strong> termed the dispersion signal. The signal is called the<br />
Free Induction Decay or FID since the amplitude decays over time owing to relaxation in the x-y<br />
plane. As a result <strong>of</strong> chemical shifts <strong>and</strong> spin-spin coupling, the signal measured by the receiver<br />
coil will normally contain a number <strong>of</strong> distinct frequencies.<br />
A.6.2. Reference Signal. The first stage <strong>of</strong> processing is to ‘mix’ or ‘subtract’ a reference signal,<br />
essentially a generated signal consisting <strong>of</strong> a signal frequency below the minimum resonance frequency<br />
<strong>of</strong> interest. This leads to a signal that contains not the actual resonance frequencies, but<br />
the frequency differences between the resonance signals <strong>and</strong> the generated reference signal. These<br />
significantly lower frequencies are easier to process. The resulting signal is fed to an analogue-todigital<br />
converter to allow subsequent processing by computer.<br />
Figure 34 shows an artificially constructed example <strong>of</strong> a FID after reference mixing. (The FID<br />
wave<strong>for</strong>m is a section <strong>of</strong> 1D 1 H spectrum <strong>of</strong> glucose, with the decay significantly enhanced to<br />
illustrate the <strong>for</strong>m <strong>of</strong> a decaying FID.)<br />
63
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Intensity<br />
0<br />
Figure 34. An example <strong>of</strong> a Free Induction Decay (FID) signal after reference mixing.<br />
A.6.3. Pre-Fourier Trans<strong>for</strong>m Processing. To convert the digital time-domain FID to a frequencydomain<br />
spectrum, a Fourier trans<strong>for</strong>m is used. However, further processing <strong>of</strong> the signal may occur<br />
prior to the Fourier trans<strong>for</strong>m. Zero-filling may be used to extend a FID that has decayed to zero in<br />
order to improve resolution[9]. Often the FID may be multiplied by a window function, to change<br />
the amplitude <strong>of</strong> the signal over time. For example, the original FID, f(t) may be multiplied by<br />
a function such as a squared cosine curve (over the first two quadrants) to give a modified FID<br />
f ′ (t):<br />
f ′ 2 t<br />
(t) = cos π f(t) (A.22)<br />
tN−1<br />
where tN−1 is the time index <strong>of</strong> the last data point in the FID. The effect <strong>of</strong> the window function<br />
can be to increase the signal-to-noise ratio, improve resolution or modify peak shape[9].<br />
A.6.4. Fourier Trans<strong>for</strong>m. A discrete Fourier trans<strong>for</strong>m is used to convert the time-domain FID<br />
to a frequency-domain spectrum. If f(t) is the FID <strong>of</strong> N points indexed 0 to N − 1, then the<br />
frequency spectrum, F(ν) is given by:<br />
Time<br />
F( j<br />
M νsamp)<br />
N−1 2πi −<br />
= f(tk)e N jk<br />
k=0<br />
(A.23)<br />
where νsamp is the sampling frequency <strong>of</strong> the FID, <strong>and</strong> M the number <strong>of</strong> points in the discrete<br />
Fourier trans<strong>for</strong>m, <strong>and</strong> the index j is between 0 <strong>and</strong> M/2.<br />
A.6.5. Phase Correction. The resulting discrete frequency spectrum, F(ν), takes complex values.<br />
The real <strong>and</strong> imaginary parts <strong>of</strong> the spectrum may be interpreted as the absorption <strong>and</strong> dispersion<br />
mode signals corresponding to signals that are in phase <strong>and</strong> π/2 out <strong>of</strong> phase with the generated<br />
reference signal. (Figure 35 shows the typical <strong>for</strong>m <strong>of</strong> absorption <strong>and</strong> dispersion signals.)<br />
Ideally, the phase <strong>of</strong> the generated reference signal should match that <strong>of</strong> the precessing net<br />
magnetic moment, but when this does not occur, each part <strong>of</strong> the complex spectrum may be a<br />
mixture <strong>of</strong> absorption <strong>and</strong> dispersion mode signals. In this case it is necessary to phase correct<br />
the spectrum so that the real part <strong>of</strong> the spectrum is the absorption signal. A phase correction <strong>of</strong><br />
θ can be made by trans<strong>for</strong>ming the spectrum F(ν) as follows (a compact <strong>for</strong>m <strong>of</strong> equations given<br />
in [9]):<br />
F ′ (ν) = F(ν)e −iθ<br />
(A.24)<br />
A.6.6. 1D <strong>NMR</strong> Spectrum Plot. Normally the real part <strong>of</strong> the spectrum, containing the absorption<br />
signal is considered. By convention, the spectrum is plotted with higher frequency, or higher ppm<br />
values, to the left[14]. Figure 36 shows an example <strong>of</strong> a 1D spectrum.<br />
64
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
Intensity<br />
Intensity<br />
x 106<br />
10<br />
8<br />
6<br />
4<br />
2<br />
0<br />
−2<br />
−2<br />
−4<br />
−6<br />
0.08<br />
x 106<br />
6<br />
4<br />
2<br />
0<br />
0.08<br />
0.06<br />
0.06<br />
0.04<br />
0.04<br />
0.02<br />
0<br />
Frequency ( 1 H) / ppm<br />
0.02<br />
0<br />
Frequency ( 1 H) / ppm<br />
Figure 35. Absorption (a) <strong>and</strong> dispersion (b) signals corresponding to the resonance<br />
frequency <strong>of</strong> the reference compound in a 1D 1 H spectrum <strong>of</strong> glucose.<br />
Intensity<br />
x 107<br />
3.5<br />
2.5<br />
1.5<br />
0.5<br />
−0.5<br />
4.2<br />
A.7. Multi-Dimensional <strong>NMR</strong>.<br />
3<br />
2<br />
1<br />
0<br />
4<br />
3.8<br />
3.6<br />
Frequency ( 1 H) / ppm<br />
Figure 36. A section <strong>of</strong> a 1D 1 H <strong>NMR</strong> spectrum <strong>of</strong> glucose.<br />
A.7.1. Pulse Sequences. In the description <strong>of</strong> 1D <strong>NMR</strong> above, a single RF frequency pulse that<br />
rotates the net magnetic moment by π/2 is applied to the sample <strong>and</strong> the experiment measures<br />
the resonance frequency <strong>of</strong> nuclei in a range <strong>of</strong> the spectrum. In higher dimensional <strong>NMR</strong>, a more<br />
complicated pulse sequence is applied to the sample be<strong>for</strong>e a FID is acquired. The pulse sequence<br />
65<br />
3.4<br />
−0.02<br />
−0.02<br />
−0.04<br />
−0.04<br />
3.2<br />
−0.06<br />
−0.06<br />
3
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Intensity<br />
0<br />
ν 2<br />
Figure 37. Representation <strong>of</strong> a series <strong>of</strong> FIDs taken over changing t1 values <strong>and</strong><br />
Fourier-trans<strong>for</strong>med in the first dimension to give ν2 frequencies. The diagram<br />
shows the phase change in the two peaks with t1.<br />
<strong>and</strong> FID acquisition are repeated a number <strong>of</strong> times with one or more parameters that control the<br />
timing <strong>of</strong> part <strong>of</strong> pulse sequence changing on each run. It is these extra parameters that give rise<br />
to the additional dimensionality <strong>of</strong> the results: <strong>for</strong> example, a single timing parameter, t1, in the<br />
pulse sequence creates a single additional dimension in <strong>2D</strong> <strong>NMR</strong>. 12<br />
The effect <strong>of</strong> the t1 timing parameter within the pulse sequence is <strong>of</strong>ten to change the initial<br />
direction <strong>of</strong> the net magnetic moment in the x-y plane after the final pulse be<strong>for</strong>e the FID is<br />
acquired. The type <strong>of</strong> pulse sequence applied determines what factors influence the change in the<br />
initial direction. For example, the direction change may be related to precession owing to the<br />
resonance frequency <strong>of</strong> a neighbouring nucleus, X, rather than the nucleus, A, whose resonance<br />
frequency is measured in the FID. In this case, during t1, the angle <strong>of</strong> the moment will ‘evolve’ at<br />
an angular velocity equivalent to the resonance frequency <strong>of</strong> X, so as t1 increases, the change in<br />
direction <strong>of</strong> the moment when the FID begins to be acquired increases in proportion.<br />
A.7.2. Second Fourier Trans<strong>for</strong>m. In processing <strong>2D</strong> <strong>NMR</strong>, each <strong>of</strong> the series <strong>of</strong> FIDs is first processed<br />
as above to create a series <strong>of</strong> frequency spectra, Ft1(ν). The difference in initial direction<br />
<strong>of</strong> net magnetic moment owing to t1 results in each <strong>of</strong> the frequency spectra having a different<br />
phase. When the same point is considered across the series <strong>of</strong> spectra, i.e. the sequence Ft1(ν2)<br />
<strong>for</strong> fixed frequency ν2 <strong>and</strong> varying t1, the phase will change with t1 sinusoidally.<br />
Figure 37 is a representation <strong>of</strong> the change in phase with t1. Each 1D spectrum after Fouriertrans<strong>for</strong>m<br />
in the first dimension has two peaks, but the phase <strong>of</strong> the peaks changes with t1. The<br />
period <strong>of</strong> the phase change with respect to t1 is different <strong>for</strong> each peak <strong>and</strong> is equivalent to the<br />
frequency <strong>of</strong> the peak in the second dimension.<br />
12 The notation t1 distinguishes the parameter from t2 which denotes the time during which the FID is acquired,<br />
which itself is related to the constant T2 describing the transverse relaxation decay (see section A.3.2).<br />
66<br />
t 1
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Figure 38. A section <strong>of</strong> a <strong>2D</strong> gradient-selected 1 H– 13 C HSQC <strong>NMR</strong> spectrum <strong>of</strong> glucose.<br />
To derive this second spectral frequency, a second discrete Fourier trans<strong>for</strong>m is applied in turn<br />
to the sequence Ft1(ν2) (fixed ν2, varying t1) at each ν2 value, to give a <strong>2D</strong> frequency spectrum,<br />
Φ(ν1, ν2).<br />
A.7.3. <strong>2D</strong> <strong>NMR</strong> Spectrum Plot. The ν2 frequency, i.e. that determined from the FID, is called<br />
the F2 frequency or ppm <strong>and</strong> is plotted on the horizontal axis. The frequency derived from the<br />
change in phase with t1 is called F1 <strong>and</strong> plotted on the vertical axis. An example <strong>of</strong> <strong>2D</strong> spectrum<br />
is shown in Figure 38.<br />
A.7.4. Types <strong>of</strong> Multi-Dimensional <strong>NMR</strong> Experiments. A wide variety <strong>of</strong> <strong>2D</strong>, <strong>and</strong> higher dimensional,<br />
<strong>NMR</strong> experiments are possible, characterised by pulse sequences that measure specific<br />
properties <strong>of</strong> the molecular structure. For example, in this project the <strong>2D</strong> spectra result from<br />
Heteronuclear Single Quantum Coherence (HSQC) experiments that identifies the resonance frequencies<br />
<strong>of</strong> 13 C nuclei connected via a single bond to 1 H.<br />
A.8. <strong>NMR</strong> Sensitivity. The sensitivity <strong>of</strong> an <strong>NMR</strong> experiment <strong>of</strong> a measure <strong>of</strong> its ability to<br />
distinguish genuine signals from background noise.<br />
A.8.1. Factors Affecting Sensitivity. A number <strong>of</strong> factors influence the sensitivity <strong>of</strong> an <strong>NMR</strong><br />
experiment[9], including:<br />
• the probe used to detect the rotating net magnetic moment;<br />
• the signal processing equipment such as amplifiers <strong>and</strong> analogue-to-digital converters;<br />
• the stability <strong>and</strong> homogeneity <strong>of</strong> the magnetic field;<br />
• the nature <strong>of</strong> the experiment itself.<br />
A.8.2. Signal-Averaging. The effect <strong>of</strong> noise can be reduced by signal-averaging: two or more<br />
equivalent spectra are combined resulting in an increase in peak intensity but less <strong>of</strong> an increase in<br />
the noise. For r<strong>and</strong>om noise, the improvement in sensitivity is √ n <strong>for</strong> averaging over n spectra[9].<br />
Note, however, that the t1-noise described in this project is not entirely r<strong>and</strong>om <strong>and</strong> is not reduced<br />
to this extent by signal-averaging. Additionally, the length <strong>of</strong> time taken to acquire <strong>2D</strong> spectra<br />
limits the use <strong>of</strong> signal-averaging.<br />
67
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
A.8.3. Signal-to-Noise Ratio. A st<strong>and</strong>ard metric <strong>for</strong> the sensitivity is the (root-mean-square or<br />
RMS) Signal-to-Noise Ratio (SNR), calculated as:<br />
SNR = Φ(p)<br />
σ (n)<br />
(A.25)<br />
where Φ (p) is the intensity <strong>of</strong> a specific peak <strong>and</strong> σ (n) is the st<strong>and</strong>ard deviation <strong>of</strong> the noise in the<br />
neighbourhood <strong>of</strong> the peak. In some definitions, the denominator is taken to be twice the noise<br />
st<strong>and</strong>ard deviation[9].<br />
An alternative measure is the Peak-To-Peak SNR that compares the signal amplitude to the<br />
maximum amplitude <strong>of</strong> the noise, rather than its st<strong>and</strong>ard deviation. Usually the maximum<br />
amplitude is assumed to be 2.5 times the st<strong>and</strong>ard deviation[9].<br />
68
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Appendix B. Wavelet <strong>Analysis</strong><br />
The theory <strong>of</strong> wavelets grew from the desire to study the local frequency composition <strong>of</strong> localised<br />
<strong>and</strong> <strong>of</strong>ten noisy time signals that did not have the periodic behaviour required <strong>for</strong> other techniques,<br />
such as Fourier analysis. Although the concept <strong>of</strong> wavelets had arisen in a number <strong>of</strong> fields during<br />
the Twentieth Century, the mathematics <strong>of</strong> modern wavelet analysis is taken to have started with<br />
the analysis <strong>of</strong> seismic data in the 1980s [1, 18, 23]. Continuing research, especially in the 1990s,<br />
has lead to a wide range <strong>of</strong> applications leveraging wavelet analysis [1].<br />
This appendix focuses on the theory underlying the application <strong>of</strong> wavelets in this project.<br />
B.1. Continuous Wavelet Trans<strong>for</strong>m.<br />
B.1.1. Square-Integrable Functions. Wavelet analysis operates on functions that are Lebesgue measurable<br />
<strong>and</strong> ‘square-integrable’ in terms <strong>of</strong> the Lebesgue integral. In addition, the wavelets considered<br />
here operate on functions <strong>of</strong> the real line.<br />
Definition B.1 (Square-Integrable). The set L2 (R) <strong>of</strong> square-integrable functions <strong>of</strong> one real<br />
variable 13 is defined as:<br />
L 2 <br />
∞<br />
(R) = f : R → R such that |f(t)| 2 <br />
dt < ∞<br />
(B.1)<br />
where integration is the Lebesgue integral.<br />
B.1.2. Function Energy <strong>and</strong> Localisation. The value <strong>of</strong> ∞<br />
−∞ |f(t)|2dt is <strong>of</strong>ten termed the energy,<br />
E, <strong>of</strong> the function. The condition on a finite energy implies that such functions in L2 (R) are<br />
localised in the sense that they must ‘decay’ to 0 at ±∞ [5]. The localisation can be quantified by<br />
considering the mean time, ¯t, as a measure <strong>of</strong> the function’s ‘centre’, <strong>and</strong> time st<strong>and</strong>ard deviation,<br />
σt, as a measure <strong>of</strong> its ‘spread’, defined as follows [23]:<br />
¯t = 1<br />
E<br />
σt 2 = 1<br />
E<br />
∞<br />
−∞<br />
∞<br />
−∞<br />
−∞<br />
t|f(t)| 2 dt (B.2)<br />
(t − ¯t) 2 |f(t)| 2 dt (B.3)<br />
where the normalising factor, E, is the energy. The same localisation is true <strong>of</strong> the frequency<br />
components <strong>of</strong> the signal represented by the function. If the Fourier trans<strong>for</strong>m <strong>of</strong> f(t) is denoted<br />
by ˆ f(ν), where<br />
ˆf(ν) =<br />
∞<br />
−∞<br />
f(t)e −2πiνt dt (B.4)<br />
then the mean frequency, ¯ν, <strong>and</strong> frequency st<strong>and</strong>ard deviation, σν, are defined as:<br />
¯ν = 1<br />
E<br />
σν 2 = 1<br />
E<br />
∞<br />
−∞<br />
∞<br />
−∞<br />
ν| ˆ f(ν)| 2<br />
dν (B.5)<br />
(ν − ¯ν) 2 | ˆ f(ν)| 2<br />
dν (B.6)<br />
Since, by Parseval’s theorem, ∞<br />
−∞ | ˆ f(ν)| 2<br />
dν = ∞<br />
−∞ |f(t)|2 dt, the normalising factor is the same.<br />
B.1.3. Inner Product. To analyse the components <strong>of</strong> a function f(t) in L2 (R), a sensible approach<br />
is to compare it to a reference function, say ψ(t), also in L2 (R), <strong>and</strong> as a measure <strong>of</strong> similarity,<br />
use the inner product:<br />
〈f, ψ〉 =<br />
∞<br />
−∞<br />
f(t)ψ(t)dt (B.7)<br />
Here ψ(t) represents the complex conjugate <strong>of</strong> ψ(t); <strong>for</strong> the real functions under consideration at<br />
this point, this distinction is not relevant.<br />
13 The variable t is chosen here since in many applications the function represents a signal that varies with time.<br />
69
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
B.1.4. Translation <strong>and</strong> Dilation. Since ψ(t) is a member <strong>of</strong> L2 (R), it will also be localised in both<br />
the time <strong>and</strong> frequency domain as described above, so the inner product as measure <strong>of</strong> similarity<br />
will be restricted to a range <strong>of</strong> times <strong>and</strong> frequencies characteristic <strong>of</strong> ψ(t). To be useful as a<br />
method to analyse the composition <strong>of</strong> the entire signal f(t), it is there<strong>for</strong>e necessary to ‘move’<br />
ψ(t) in both domains. This is achieved by means <strong>of</strong> a translation by a factor b ∈ R, <strong>and</strong> dilation<br />
by a factor a ∈ R (a = 0) to produce the family <strong>of</strong> functions:<br />
ψ (a,b)(t) = 1<br />
<br />
t − b<br />
ψ . (B.8)<br />
|a| a<br />
The factor 1/ |a| is introduced <strong>for</strong> convenience as it ensures that the energy is the same <strong>for</strong> all<br />
values <strong>of</strong> a.<br />
B.1.5. Wavelets <strong>and</strong> Continuous Wavelet Trans<strong>for</strong>m. If the mean time <strong>and</strong> frequency <strong>of</strong> ψ(t) are<br />
¯tψ <strong>and</strong> ¯νψ, by applying (B.2) <strong>and</strong> (B.5) to ψ (a,b)(t) <strong>and</strong> its Fourier trans<strong>for</strong>m, it can be seen that<br />
the mean time <strong>and</strong> mean frequency are now ¯tψ + b <strong>and</strong> ¯νψ/a. Thus the inner product <strong>of</strong> f(t) <strong>and</strong><br />
ψ (a,b)(t) is a measure <strong>of</strong> frequency components centred on ¯νψ/a near the time location ¯tψ + b. By<br />
varying a <strong>and</strong> b, this allows the local analysis <strong>of</strong> frequency components <strong>of</strong> f(t) at the entire range<br />
<strong>of</strong> times. This approach by <strong>for</strong>malised by defining the reference function as a wavelet, <strong>and</strong> the<br />
inner product with the wavelet as the continuous wavelet trans<strong>for</strong>m.<br />
Definition B.2 (Wavelet). A function ψ(t) ∈ L2 (R) is a wavelet, if it satisfies the admissibility<br />
condition:<br />
∞<br />
|<br />
Cψ =<br />
ˆ f(ν)| 2<br />
dν < ∞<br />
ˆf(ν)<br />
(B.9)<br />
The value Cψ is the admissibility constant. 14<br />
−∞<br />
Definition B.3 (Continuous Wavelet Trans<strong>for</strong>m). If f(t) ∈ L2 (R) <strong>and</strong> ψ(t) is a wavelet, then<br />
(Wψf), the Continuous Wavelet Trans<strong>for</strong>m (CWT) <strong>of</strong> f(t), is defined as:<br />
<br />
1 t − b<br />
(Wψf)(a, b) = f, ψ<br />
|a| a<br />
<br />
(B.10)<br />
One consequence <strong>of</strong> the admissibility condition is that ˆ f(0) must be 0 <strong>for</strong> Cψ to be finite. Using<br />
(B.4),<br />
0 = ˆ f(0)<br />
=<br />
=<br />
∞<br />
−∞<br />
∞<br />
−∞<br />
f(t)e −2πi0t dt<br />
f(t)dt (B.11)<br />
Thus, a wavelet has a mean value <strong>of</strong> zero.<br />
Note that application <strong>of</strong> (B.3) <strong>and</strong> (B.6) shows that the time <strong>and</strong> frequency st<strong>and</strong>ard deviations<br />
<strong>of</strong> ψ (a,b)(t) are a¯tψ <strong>and</strong> ¯νψ/a respectively, where ¯tψ <strong>and</strong> ¯νψ are the corresponding values <strong>for</strong> ψ(t).<br />
This means that as the frequency st<strong>and</strong>ard deviation decreases, i.e. the CWT measures a tighter<br />
range <strong>of</strong> frequencies, the time st<strong>and</strong>ard deviation <strong>of</strong> increases meaning that the measurement<br />
is less localised in the time-domain, <strong>and</strong> vice versa. This adaptive behaviour distinguishes the<br />
behaviour <strong>of</strong> wavelets from the short-time Fourier trans<strong>for</strong>m where the ‘resolutions’ in the time<br />
<strong>and</strong> frequency domains remain constant, <strong>and</strong> makes wavelet analysis more sensitive to rapidly<br />
changing signals[23].<br />
To visualise the results <strong>of</strong> the CWT, the values <strong>of</strong> (Wψf)(a, b) or |(Wψf)(a, b)| 2 are plotted (the<br />
latter being termed a scalogram[23]), with a on the vertical axis, sometimes using a logarithmic<br />
scale, <strong>and</strong> b on the horizontal axis.<br />
14 Complex wavelets have an additional constraint on the <strong>for</strong>m <strong>of</strong> ˆ f [1].<br />
70
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
ψ(t)<br />
1<br />
0.5<br />
0<br />
−0.5<br />
−5 −4 −3 −2 −1 0 1 2 3 4 5<br />
Figure 39. The Mexican Hat wavelet<br />
B.1.6. CWT Example. Figure 39 shows an example <strong>of</strong> a wavelet function: the ‘Mexican Hat’<br />
wavelet defined as [1]:<br />
ψ(t) =<br />
t<br />
2<br />
√<br />
4 3 √ π (1 − t2 t2 −<br />
)e 2 (B.12)<br />
An example <strong>of</strong> CWT using the Mexican Hat wavelet is shown in Figure 40. The signal consists<br />
<strong>of</strong> two sinusoidal waves <strong>of</strong> different periods <strong>and</strong> changing amplitudes. The pseudocolour plot <strong>of</strong><br />
the CWT <strong>for</strong> different values <strong>of</strong> the dilation factor, or scale, a, <strong>and</strong> translation factor, or position,<br />
b. The plot is coloured according to the value <strong>of</strong> |(Wψf)(a, b)|, with higher magnitudes plotted<br />
using lighter shades.<br />
The change in dominant frequency with position can be seen in the CWT map, <strong>and</strong> the two<br />
separate frequency components can be cleary distinguished even at locations where they are convoluted<br />
together in the signal. The periodic nature <strong>of</strong> the signals is shown by the regular pattern<br />
<strong>of</strong> light <strong>and</strong> dark b<strong>and</strong>s as the position changes. The light b<strong>and</strong>s correspond to locations where the<br />
dilated <strong>and</strong> translated wavelet matches the signal closely, effectively ‘in phase’, or π out <strong>of</strong> phase,<br />
with the signal, resulting in a large magnitude <strong>of</strong> the inner product. Since the shades represent<br />
the magnitude rather than value <strong>of</strong> the CWT, the map does not distinguish between in phase<br />
<strong>and</strong> π out <strong>of</strong> phase. Conversely, the dark b<strong>and</strong>s are where the signal <strong>and</strong> translated wavelet are<br />
out <strong>of</strong> phase by π/2 or 3π/2, resulting in a small magnitude <strong>for</strong> the inner product. The change<br />
in component amplitude with position is reflected in the changes in relative brightness <strong>of</strong> the<br />
light b<strong>and</strong>s: the brightest parts <strong>of</strong> the map—at approximately (a = 16, b = 275) <strong>and</strong> (a = 6,<br />
b = 400)—correspond to the location <strong>of</strong> the maximum amplitude <strong>of</strong> each <strong>of</strong> the two frequency<br />
components.<br />
B.1.7. Inverse Wavelet Trans<strong>for</strong>m. The CWT could be per<strong>for</strong>med using any function ψ(t) ∈<br />
L 2 (R), even if it does not satisfy the admissibility condition. However, the finite value <strong>of</strong> Cψ <strong>for</strong><br />
the wavelet function enables an inverse to the CWT.<br />
Definition B.4 (Inverse Wavelet Trans<strong>for</strong>m). If the (Wψf)(a, b) is the Continuous Wavelet Trans<strong>for</strong>m<br />
<strong>of</strong> f(t), then f(t) can be reconstructed from (Wψf) using the Inverse Wavelet Trans<strong>for</strong>m:<br />
f(t) = 1<br />
Cψ<br />
∞ ∞<br />
where ψ (a,b)(t) is the translated <strong>and</strong> dilated wavelet defined by (B.8)<br />
−∞<br />
−∞<br />
A derivation <strong>of</strong> the Inverse Wavelet Trans<strong>for</strong>m is given in [5].<br />
(Wψf)(a, b)ψ (a,b)(t) da<br />
db (B.13)<br />
a2 B.2. Discrete Wavelet Trans<strong>for</strong>m. Although the Inverse Wavelet Trans<strong>for</strong>m can be used to<br />
reconstruct the signal from the CWT, there is a lot <strong>of</strong> redundancy in the CWT, in the sense that<br />
much in<strong>for</strong>mation about the original signal, f(t), carried in a particular value (Wψf)(a ′ , b ′ ) is<br />
also carried by ‘nearby’ values such as (Wψf)(a ′ + δa, b ′ + δb). Instead <strong>of</strong> the redundant CWT<br />
representation, many wavelet applications make use <strong>of</strong> a wavelet representation <strong>of</strong> signal that<br />
samples the CWT using discrete values <strong>of</strong> a <strong>and</strong> b.<br />
71
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(b)<br />
(c)<br />
(d)<br />
f 1 (t)<br />
f 2 (t)<br />
f(t)<br />
Scale (a)<br />
1<br />
0.5<br />
0<br />
−0.5<br />
−1<br />
0 100 200 300 400 500 600 700<br />
1<br />
0.5<br />
0<br />
−0.5<br />
−1<br />
0 100 200 300 400 500 600 700<br />
1<br />
0.5<br />
0<br />
−0.5<br />
−1<br />
0 100 200 300 400 500 600 700<br />
31<br />
29<br />
27<br />
25<br />
23<br />
21<br />
19<br />
17<br />
15<br />
13<br />
11<br />
9<br />
7<br />
5<br />
3<br />
1<br />
t<br />
t<br />
t<br />
100 200 300<br />
Position (b)<br />
400 500 600<br />
Figure 40. An example <strong>of</strong> CWT analysis <strong>of</strong> a periodic signal. The components<br />
<strong>of</strong> the signal are shown in (a) <strong>and</strong> (b): sinusoidal waves <strong>of</strong> period 50 <strong>and</strong> 20,<br />
π/2 out <strong>of</strong> phase with one other <strong>and</strong> with amplitudes modulated by a Gaussian.<br />
The combined signal is shown in (c). (d) is a pseudocolour plot the CWT <strong>of</strong> the<br />
combined signal using the Mexican Hat wavelet; values with a greater magnitude<br />
are shown in lighter shades.<br />
72
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
B.2.1. Dyadic Grid. Typically a dyadic grid is used that per<strong>for</strong>ms a logarithmic discretisation <strong>of</strong><br />
both the dilation <strong>and</strong> translation parameters, such that:<br />
a = 2 m<br />
b = 2 m nb0 where m, n ∈ Z, b0 > 0 (B.14)<br />
The value b0 is termed the sampling rate.<br />
For simplicity, b0 is <strong>of</strong>ten taken to be 1. The notation ψm,n will be used the translated <strong>and</strong><br />
dilated wavelet at the location on the grid defined by m <strong>and</strong> n at the sampling rate <strong>of</strong> 1. (The<br />
lack <strong>of</strong> parentheses is used to distinguish this notation from that used in (B.8).)<br />
m −<br />
ψm,n(t) = ψ (2m ,2mn)(t) = 2 2 ψ<br />
B.2.2. Discrete Wavelet Trans<strong>for</strong>m.<br />
m t − 2 n<br />
2 m<br />
m −<br />
= 2 2 ψ 2 −m t − n <br />
(B.15)<br />
Definition B.5 (Wavelet Coefficients <strong>and</strong> Discrete Wavelet Trans<strong>for</strong>m). The value dm,n <strong>of</strong> the<br />
CWT at the position in the dyadic grid defined by m <strong>and</strong> n is termed the wavelet coefficient or<br />
detail coefficient. The trans<strong>for</strong>m from f(t) to wavelet coefficients is the Discrete Wavelet Trans<strong>for</strong>m<br />
(DWT) 15<br />
dm,n = 〈f(t), ψm,n(t)〉<br />
m −<br />
= 2 2<br />
∞<br />
−∞<br />
f(t)ψ 2 −m t − n dt (B.16)<br />
B.2.3. Stability Condition. For this representation as wavelet coefficients to be useful, the family<br />
<strong>of</strong> wavelet functions, {ψm,n(t)}, must meet a further condition, termed the stability condition:<br />
Definition B.6 (Stability Condition). The family <strong>of</strong> wavelet functions {ψm,n(t)} generated from<br />
the wavelet ψ(t) by (B.15) satisfy the stability condition if there exists constants A <strong>and</strong> B, 0 <<br />
A ≤ B < ∞, such that,<br />
AE ≤ <br />
|dm,n| 2 ≤ BE ∀f(t) ∈ L 2 (R) (B.17)<br />
m,n∈Z<br />
where dm,n are the wavelet coefficients defined in (B.16), <strong>and</strong> E is the energy <strong>of</strong> f(t).<br />
In simple terms, the stability condition ensures <strong>for</strong> functions that are ‘close’ in L 2 (R) have<br />
representations in terms <strong>of</strong> wavelet coefficients that are also ‘close’, <strong>and</strong> vice versa [23]. More<br />
accurately, the stability condition ensures that the wavelet family {ψm,n(t)} is a frame <strong>of</strong> L 2 (R)<br />
[5]. If the constants in (B.17) are such that A = B then the frame is termed a tight frame.<br />
B.2.4. Inverse Discrete Wavelet Trans<strong>for</strong>m. A result arising from the general theory <strong>of</strong> frames<br />
[23] is that the original function f(t) can be reconstructed from its wavelet coefficient as follows.<br />
Definition B.7 (Inverse Discrete Wavelet Trans<strong>for</strong>m). If dm,n are the wavelet coefficients given<br />
by the CWT, then the original function f(t) can be reconstructed as:<br />
∞ ∞<br />
f(t) = dm,n ψm,n(t) (B.18)<br />
m=−∞ n=−∞<br />
where the (non-unique) functions ψm,n are termed the dual functions <strong>for</strong> the frame {ψm,n(t)}.<br />
A simplification exists <strong>for</strong> tight frames, where the functions { 1<br />
Aψm,n(t)} (A is the constant in<br />
the stability condition (B.17)) are a suitable choice <strong>for</strong> the dual functions. In the case where<br />
A = B = 1, this gives:<br />
∞ ∞<br />
f(t) = dm,nψm,n(t) (B.19)<br />
m=−∞ n=−∞<br />
15 The term Discrete Wavelet Trans<strong>for</strong>m may instead be used to refer to the Fast Wavelet Trans<strong>for</strong>m described<br />
below, <strong>and</strong> in particular, the Pyramid Algorithm <strong>for</strong> discrete time signals [18].<br />
73
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
B.2.5. Wavelet basis <strong>of</strong> L 2 (R). The <strong>for</strong>m <strong>of</strong> (B.19) suggests that {ψm,n(t)} is a basis <strong>for</strong> the space<br />
L 2 (R). (A detailed treatment in terms <strong>of</strong> Riesz bases is given by [5].) In the case where A = B = 1<br />
the basis is orthogonal [23], i.e.:<br />
〈ψm,n, ψm ′ ,n ′〉 =<br />
<br />
E m = m ′ <strong>and</strong> n = n ′<br />
0 otherwise<br />
(B.20)<br />
where E is the energy <strong>of</strong> ψm,n. Usually a normalizing factor is chosen <strong>for</strong> the wavelet, ψ(t), <strong>and</strong><br />
the wavelet family, {ψm,n(t)} so that the energy is 1, <strong>and</strong> the family <strong>for</strong>ms an orthonormal basis.<br />
A further consequence <strong>of</strong> choosing wavelet functions such that A = B = 1 is that the wavelet<br />
coefficients generated by the DWT represent the original signal with no redundancy [23].<br />
B.3. Scaling Functions. The basis <strong>of</strong> L 2 (R) <strong>for</strong>med by the family {ψm,n} can be considered as<br />
a direct sum <strong>of</strong> subspaces L 2 (R) spanned by the subsets <strong>of</strong> the <strong>for</strong>m Ψm = {ψm,n : n ∈ Z}, i.e.<br />
those functions having the same value <strong>of</strong> m (the same dilation) [5]. If subspace <strong>for</strong>med by the<br />
(closure in L 2 (R)) <strong>of</strong> the linear span <strong>of</strong> functions in Ψm is denoted Wm, then:<br />
L 2 (R) =<br />
∞<br />
k=−∞<br />
It is useful to consider the sequence <strong>of</strong> subspaces Vm defined by:<br />
Vm =<br />
∞<br />
k=m+1<br />
Wk<br />
Wk<br />
(B.21)<br />
(B.22)<br />
The analysis <strong>of</strong> these subspaces gives rise to scaling functions from which wavelets can be constructed.<br />
In addition, scaling functions are used in a fast algorithm <strong>for</strong> calculating the DWT <strong>of</strong><br />
discrete functions, described below.<br />
B.3.1. Scaling Function <strong>and</strong> Approximation Coefficients. The scaling function, φ(t), is defined<br />
here in terms <strong>of</strong> the subspaces Vm.<br />
Definition B.8 (Scaling Function). If φ(t) is translated <strong>and</strong> dilated in an equivalent <strong>for</strong>m to the<br />
wavelet on the dyadic grid, to define:<br />
m −<br />
φm,n(t) = 2 2 φ 2 −m t − n <br />
(B.23)<br />
then φ(t) is a scaling function if the set Φm = {φm,n : n ∈ Z} is an orthonormal basis <strong>of</strong> Vm. In<br />
addition, the scaling function is usually normalised as follows [1, 24]. Note that this normalisation<br />
considers the function itself rather than its energy.<br />
∞<br />
−∞<br />
φ(t)dt = 1 (B.24)<br />
(The properties <strong>of</strong> the scaling function, together with the properties <strong>of</strong> the subspaces Vm,<br />
constitute a Multiresolution <strong>Analysis</strong> [23].)<br />
Since {φm,n} is a basis <strong>for</strong> Vm, s(t) ∈ Vm may decomposed as:<br />
s(t) =<br />
where the coefficients sm,n are given by:<br />
<strong>and</strong> termed approximation coefficients.<br />
∞<br />
n=−∞<br />
sm,nφm,n(t) (B.25)<br />
sm,n = 〈f, φm,n〉 (B.26)<br />
74
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
B.3.2. Decomposition <strong>of</strong> L 2 (R) by Wavelet <strong>and</strong> Scaling Functions. From the definition <strong>of</strong> Vm in<br />
(B.22) <strong>and</strong> the decomposition <strong>of</strong> L 2 (R) in (B.21), <strong>for</strong> a specific value m = m ′ ,<br />
L 2 (R) = Vm ′ ⊕ Wm ′ ⊕ Wm ′ −1 ⊕ Wm ′ −2 ⊕ · · · (B.27)<br />
This suggest that any function, f(t) ∈ L2 (R), may be written as a function s(t) ∈ Vm ′, plus the<br />
combination <strong>of</strong> wavelet functions that <strong>for</strong>m the basis <strong>for</strong> Wm ′ <strong>and</strong> lower subspaces (corresponding<br />
to dilated wavelets with increasingly higher mean frequencies):<br />
f(t) =<br />
∞<br />
n=−∞<br />
sm ′ ,nφm ′ ,n(t) +<br />
∞<br />
∞<br />
m=m ′ n=−∞<br />
dm,nψm ′ ,n(t) (B.28)<br />
As a consequence <strong>of</strong> (B.24), ∞<br />
−∞ φm,n(t)dt = 1, <strong>and</strong> so the approximation coefficients can<br />
be interpreted as a weighted average <strong>of</strong> f(t) given by a particular translation <strong>of</strong> the φ(t) (<strong>and</strong><br />
dilated corresponding to Vm) [1]. The function s(t) there<strong>for</strong>e gives an approximation to the<br />
original function f(t), with the difference between this approximation <strong>and</strong> the original function<br />
represented by the series <strong>of</strong> wavelet coefficients at levels m ′ , m ′ +1, m ′ +2, . . .. As m ′ decreases the<br />
approximation reconstructed from the approximation coefficients becomes coarser as the resolution<br />
<strong>of</strong> the scaling functions in Φm is dilated.<br />
B.3.3. Scaling Equation. From the construction in (B.22) it can be seen that the subspaces Vm<br />
are nested:<br />
· · · ⊂ Vm+1 ⊂ Vm ⊂ Vm−1 ⊂ · · · (B.29)<br />
As it is a member <strong>of</strong> the basis <strong>of</strong> Vm, φm,0 ∈ Φm, is a member <strong>of</strong> Vm. Since Vm ⊂ Vm−1, φm,0 can<br />
be written in terms <strong>of</strong> the basis <strong>of</strong> Vm−1, i.e.:<br />
φm,0(t) = <br />
k<br />
c ′ kφm−1,k<br />
(B.30)<br />
When written in terms <strong>of</strong> the original scaling function φ(t), equivalent to φ0,0, (<strong>and</strong> modifying the<br />
coefficients c ′ k by a factor <strong>of</strong> √ 2) this gives the following relation:<br />
Definition B.9 (Scaling Equation <strong>and</strong> Scaling Coefficients). The scaling function φ(t) is related<br />
to translated <strong>and</strong> dilated versions <strong>of</strong> itself by the scaling equation or dilution equation<br />
φ(t) = <br />
ckφ(2t − k) (B.31)<br />
where the ck are the scaling coefficients.<br />
k<br />
A key result <strong>of</strong> this approach is that the same coefficients can be used to construct the related<br />
wavelet function as follows [1]. 16<br />
ψ(t) = <br />
(−1) k c1−kφ(2t − k) (B.32)<br />
k<br />
B.4. Fast Wavelet Trans<strong>for</strong>m. The relationship between the wavelets, scaling functions <strong>and</strong><br />
scaling coefficients defined in equations (B.32) <strong>and</strong> (B.31) lead to a fast, recursive algorithm <strong>for</strong><br />
determining the approximation <strong>and</strong> detail (or wavelet) coefficients <strong>for</strong> f(t), derived as follows.<br />
16 A thorough derivation <strong>of</strong> this result is given in [5] which also notes that the general result corresponding to<br />
this equation uses the complex conjugate <strong>of</strong> c1−k.<br />
75
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
B.4.1. Forward Fast Wavelet Trans<strong>for</strong>m. From (B.31) <strong>and</strong> the definition <strong>of</strong> φm,n in (B.23),<br />
φm,n(t) = 1 <br />
√ ckφm−1,2n+k<br />
(B.33)<br />
2<br />
Using this in (B.26),<br />
sm,n =<br />
<br />
= 1<br />
√ 2<br />
= 1<br />
√ 2<br />
= 1<br />
√ 2<br />
f, 1<br />
√ 2<br />
<br />
k<br />
<br />
k<br />
<br />
k<br />
k<br />
<br />
k<br />
ckφm−1,2n+k<br />
〈f, ckφm−1,2n+k〉<br />
ck 〈f, φm−1,2n+k〉<br />
cksm−1,2n+k<br />
<br />
(B.34)<br />
This relationship allows the approximation coefficients at level m to be derived, using only the<br />
scaling coefficients, from the approximation coefficients at the level m−1 (which represents a finer<br />
approximation to the signal f(t)).<br />
The equivalent manipulation <strong>of</strong> (B.32) <strong>and</strong> definition <strong>of</strong> ψm,n in (B.15) gives:<br />
ψm,n(t) = 1 <br />
√ (−1)<br />
2<br />
k c1−kφm−1,2n+k<br />
(B.35)<br />
<strong>and</strong> the detail coefficient at level m given by (B.16) to be written as:<br />
<br />
dm,n = f, 1 <br />
√ (−1)<br />
2<br />
k<br />
k <br />
c1−kφm−1,2n+k<br />
= 1 <br />
<br />
k √ f, (−1) c1−kφm−1,2n+k<br />
2<br />
k<br />
= 1 <br />
√ (−1)<br />
2<br />
k c1−k 〈f, φm−1,2n+k〉<br />
= 1<br />
√ 2<br />
k<br />
<br />
k<br />
k<br />
(−1) k c1−ksm−1,2n+k<br />
(B.36)<br />
Thus the detail coefficients at level m can be derived from the approximation coefficients at level<br />
m − 1.<br />
The recursive relationships (B.34) <strong>and</strong> (B.36) are the <strong>for</strong>ward part <strong>of</strong> the Fast Wavelet Trans<strong>for</strong>m<br />
(FWT).<br />
B.4.2. Inverse Fast Wavelet Trans<strong>for</strong>m. The reverse procedure is to derive the approximation<br />
coefficients at level m −1 from the approximation <strong>and</strong> details coefficients at level m. From (B.22),<br />
it can be seen that,<br />
Vm−1 = Vm ⊕ Wm<br />
(B.37)<br />
meaning that a function represented by a linear sum <strong>of</strong> functions in Φm−1 (the orthonormal basis<br />
<strong>of</strong> Vm−1) can be represented a sum <strong>of</strong> functions <strong>for</strong>med from the basis Φm <strong>and</strong> Ψm respectively:<br />
<br />
sm−1,nφm−1,n(t) = <br />
sm,kφm,k(t) + <br />
dm,kψm,k(t)<br />
n<br />
(substituting from (B.33) <strong>and</strong> (B.35)),<br />
k<br />
= <br />
k<br />
sm,k<br />
k<br />
1 <br />
√ cjφm−1,2k+j(t) +<br />
2<br />
<br />
j<br />
76<br />
k<br />
dm,k<br />
1 <br />
√<br />
2<br />
j<br />
(−1) j c1−jφm+1,2k+j(t)
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(substituting n = 2k + j),<br />
= <br />
k<br />
n<br />
sm,k<br />
1 <br />
√ cn−2kφm−1,n(t) +<br />
2<br />
<br />
(changing the order <strong>of</strong> summation),<br />
= <br />
<br />
1 <br />
√ cn−2ksm,k +<br />
2<br />
1 <br />
√<br />
2<br />
Equating coefficients <strong>of</strong> φm−1,k(t) in (B.38) gives,<br />
sm−1,n = 1 <br />
√ cn−2ksm,k +<br />
2<br />
1 <br />
√<br />
2<br />
k<br />
k<br />
n<br />
k<br />
k<br />
k<br />
dm,k<br />
1 <br />
√<br />
2<br />
(−1) n−2k c 1−(n−2k)dm,k<br />
(−1) n−2k c 1−(n−2k)dm,k<br />
n<br />
(−1) n−2k c 1−(n−2k)φm−1,n(t)<br />
<br />
φm−1,n(t)<br />
(B.38)<br />
(B.39)<br />
B.4.3. Decomposition <strong>of</strong> L2 (R) by FWT. If the functions sm(t) <strong>and</strong> dm(t) are defined as the signals<br />
represented by the approximation <strong>and</strong> details coefficients at level m:<br />
∞<br />
sm(t) = sm,nφm,n(t) (B.40)<br />
dm(t) =<br />
n=−∞<br />
∞<br />
n=−∞<br />
dm,nψm,n(t) (B.41)<br />
then the decomposition <strong>of</strong> the original signal defined in (B.28) can also be represented as:<br />
∞<br />
f(t) = sm ′(t) + dm(t) (B.42)<br />
m=m ′<br />
where m ′ ∈ Z can be chosen as required. The signal sm ′ represents an approximation <strong>of</strong> f(t), <strong>and</strong><br />
as m ′ increases the approximation becomes closer to f(t). Each <strong>of</strong> the signals dm(t) is composed<br />
<strong>of</strong> dilated wavelet functions whose mean frequency decreases as m increases.<br />
B.5. Pyramid Algorithm. The FWT is <strong>of</strong>ten used to process signals where time values are<br />
discrete. For example, in this project, the <strong>NMR</strong> data sets are discrete signals. When certain<br />
assumptions on the <strong>for</strong>m <strong>of</strong> the wavelet <strong>and</strong> scaling functions are met, an efficient implementation<br />
<strong>of</strong> the FWT <strong>for</strong> discrete-time signals is possible, termed the Pyramid Algorithm[1, 18].<br />
B.5.1. Input to Pyramid Algorithm. The discrete signal is denoted by f[tn] where the {tn} are the<br />
discrete time values. Although the signal is discrete, a continuous-time equivalent, f(t), can be<br />
constructed. For example, <strong>and</strong> assuming a constant interval <strong>of</strong> 1 between the time values, a step<br />
function can be created as:<br />
f(t) =<br />
<br />
f[tn] ∃ tn such that tn − 1<br />
2 ≤ t < tn + 1<br />
2<br />
0 otherwise<br />
(B.43)<br />
The starting point <strong>for</strong> the discrete time FWT are approximation coefficients at level m = 0 <strong>of</strong><br />
the continuous-time function derived using (B.26). 17 (In some implementations <strong>of</strong> the pyramid<br />
algorithm, the discrete function values f[tn] are used instead <strong>of</strong> the approximation coefficients.<br />
This is incorrect, except where the wavelet function is the Haar wavelet in case the two sets <strong>of</strong><br />
values are the same.) This results in the set <strong>of</strong> approximation coefficients {s0,n}. Note that, in<br />
general, {s0,n} represents a signal:<br />
s0(t) =<br />
2 M −1<br />
that is only an approximation <strong>for</strong> the original discrete signal.<br />
0<br />
s0,nφ0,n(t) (B.44)<br />
17 Level m = 0 corresponds to translations <strong>of</strong> the scaling function by the sampling rate, b0, which we have taken<br />
to be 1 above. For signals where the discrete time interval is not 1, the sampling rate can be modified accordingly.<br />
77
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
B.5.2. Signal Length <strong>and</strong> Padding. In this section, the signal is assumed to be finite <strong>and</strong> that<br />
its length is such that it is represented by 2 M (M ∈ N) level 0 approximation coefficients, i.e.<br />
n ∈ {0, 1, . . ., 2 M −1}. In practical applications, a shorter signal can be padded to give the required<br />
number <strong>of</strong> coefficients. Typical methods include zero-padding where 0 values are added to one<br />
or both ends <strong>of</strong> the signal, or symmetric-padding where the part signal is repeated, in reverse, at<br />
each <strong>of</strong> the original signal. The advantage <strong>of</strong> the latter method is that it avoids creating artificial<br />
discontinuities.<br />
B.5.3. Compact Support. Additionally, it is assumed that the wavelet has sequences <strong>of</strong> non-zero<br />
scaling coefficients which are finite in length, in which case it is said to possess compact support<br />
[1]. In particular, a single finite sequence <strong>of</strong> K coefficients is assumed, with all other coefficients<br />
being zero. This enables a redefinition <strong>of</strong> the equations (B.31) <strong>and</strong> (B.32),<br />
φ(t) =<br />
K−1 <br />
k=0<br />
ckφ(2t − k) (B.45)<br />
K−1 <br />
ψ(t) = (−1) k cK−1−kφ(2t − k) (B.46)<br />
k=0<br />
The modification ensures that the wavelet <strong>and</strong> scaling function are ‘supported’ over the same<br />
finite interval [0, K − 1] [1]. The corresponding modification to the equations <strong>for</strong> the <strong>for</strong>ward<br />
FWT, (B.34) <strong>and</strong> (B.36), are:<br />
sm,n = 1<br />
K−1 <br />
√<br />
2<br />
k=0<br />
dm,n = 1<br />
K−1 <br />
√<br />
2<br />
k=0<br />
cksm−1,2n+k<br />
(−1) k cK−1−ksm−1,2n+k<br />
(B.47)<br />
(B.48)<br />
B.5.4. Wraparound. If the signal time window represented by the 2 M approximation coefficients<br />
{s0,n} is [0, T], a further simplification is to repeat the coefficients with period 2 M :<br />
s 0,n+2 M k = s0,n where k ∈ Z (B.49)<br />
<strong>and</strong> so allow the FWT equations above to refer to approximation coefficients with n indices outside<br />
the range 0 to 2 M − 1. This is equivalent to assuming the original discrete signal is periodic with<br />
period T. However, if the signal is not periodic with period T, this creates discontinuities at 0 <strong>and</strong><br />
T which can lead to large detail coefficients at the boundaries [1]. 18 An alternative interpretation<br />
is that the wavelet <strong>and</strong> scaling functions ‘wraparound’ the time window by beginning again at 0<br />
once they reach T, giving this technique its name.<br />
B.5.5. Pyramid Algorithm. The FWT can then be used to construct the approximation <strong>and</strong> detail<br />
coefficients at level m = −1 from the set {s0,n} using equations (B.47) <strong>and</strong> (B.48). The spacing<br />
<strong>of</strong> the dyadic grid at level m = 1 is twice that <strong>of</strong> level m = 0, so only 2 M−1 approximation<br />
coefficients, i.e. half those <strong>of</strong> level m = 0 are required to give the approximation <strong>of</strong> the signal in<br />
the time window [0, T]. This can be seen from the <strong>for</strong>m <strong>of</strong> the FWT equations (B.47) <strong>and</strong> (B.48):<br />
as the index n increases by 1 on the left-h<strong>and</strong> side, the corresponding indexes <strong>of</strong> the set <strong>of</strong> K<br />
approximation coefficients in the sum on the right-h<strong>and</strong> side moves by 2. Similarly, the FWT<br />
generates 2 M−1 detail coefficients to cover the time window [0, T].<br />
By recursion, the FWT constructs the approximation <strong>and</strong> detail coefficients at levels m =<br />
1, 2, . . .,M. At level m = m ′ , 2M−m′ approximation coefficients <strong>and</strong> 2M−m′ detail coefficients are<br />
produced. So, at level m = M, the FWT generates a single approximation coefficient <strong>and</strong> the<br />
approximate signal s0(t) is represented by this 1 approximation coefficient <strong>and</strong> a total <strong>of</strong> 2M − 1<br />
detail coefficients derived at this <strong>and</strong> earlier levels. Further decomposition beyond level m = M<br />
18 To avoid the discontinuities, the signal can also be ‘mirrored’ at the boundaries—the signal is repeated in<br />
reverse—as an alternative to wraparound.<br />
78
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
is not possible. For many applications the algorithm may stopped be<strong>for</strong>e level M = m. 19 In<br />
general, at level m = m ′ (1 ≤ m ′ ≤ M), the approximate original signal, s0(t), is decomposed as:<br />
s0(t) =<br />
2 M−m′ −1<br />
n=0<br />
or following the <strong>for</strong>mat <strong>of</strong> (B.42),<br />
sm ′ ,nφm ′ ,n(t) +<br />
m ′<br />
<br />
m=1<br />
m=1<br />
2 M−m −1<br />
n=0<br />
dm,nψm,n(t) (B.50)<br />
m<br />
s0(t) = sm ′(t) +<br />
′<br />
<br />
dm(t) (B.51)<br />
Note that since each wavelet, <strong>and</strong> there<strong>for</strong>e each detail signal dm(t), has a mean <strong>of</strong> zero by (B.11),<br />
so the mean value <strong>of</strong> the original signal is carried only by sm ′(t).<br />
B.5.6. Signal Decomposition by the Pyramid Algorithm. This decomposition <strong>of</strong> a discrete time<br />
signal into approximation <strong>and</strong> detail coefficients per<strong>for</strong>med by the Pyramid Algorithm described<br />
above <strong>and</strong> can be represented as follows:<br />
s0(t)<br />
s1,n ✲ s1(t)<br />
d1,n ✲<br />
d1(t)<br />
s2,n ✲ s2(t) · · ·<br />
d2,n ✲<br />
d2(t)<br />
where sm ′(t) <strong>and</strong> dm ′(t) are the approximation <strong>and</strong> details signals at level m = m′ defined in<br />
(B.42), <strong>and</strong> sm ′ ,n <strong>and</strong> dm ′ ,n are the corresponding coefficients.<br />
Figure 41 shows the decomposition by the pyramid algorithm <strong>of</strong> the signal constructed in<br />
Figure 40 from two sinusoidal signals <strong>of</strong> different frequencies. (a) is the original signal, while (b)<br />
to (j) show the detail signals at levels 1 to 9. The detail signals, dm(t), are created by applying<br />
the inverse trans<strong>for</strong>m to only the detail coefficients at level m, all other approximation <strong>and</strong> detail<br />
coefficients being set to 0. It can be seen that the higher frequency signal component is represented<br />
by larger magnitude coefficient at its location in levels 1 to 4, shown in (b), (c) <strong>and</strong> (d) <strong>and</strong> (e).<br />
The lower frequency component is represented at higher decomposition levels 4 to 8, shown in (e),<br />
(f), (g) <strong>and</strong> (h).<br />
B.5.7. Linear Algebraic Representation. This process can also be represented using linear algebra.<br />
To illustrate the <strong>for</strong>m <strong>of</strong> the matrices, an example <strong>of</strong> four non-zero scaling coefficients—c0, c1, c2,<br />
c3—is used. Let sm−1 be the column vector <strong>of</strong> length 2 M−m′ +1 consisting <strong>of</strong> the approximation<br />
coefficients produced at level m ′ − 1. Let Tm be a 2 M−m+1 × 2 M−m+1 matrix constructed from<br />
the scaling coefficients as follows:<br />
⎡<br />
⎤<br />
c0 c1 c2 c3 0 0 0 . . . 0 0 0<br />
⎢−c3<br />
c2 −c1 c0 ⎢<br />
0 0 0 . . . 0 0 0 ⎥<br />
⎢ 0 0 c0 c1 c2 c3 0 . . . 0 0 0 ⎥<br />
⎢<br />
Tm = ⎢ 0 0 −c3 c2 −c1 c0 0 . . . 0 0 0 ⎥<br />
⎢<br />
.<br />
⎢ . . . . . . . ..<br />
⎥<br />
. . . ⎥<br />
⎣ c2 c3 0 0 0 0 0 . . . 0 c0 c1⎦<br />
· · ·<br />
−c1 c0 0 0 0 0 0 . . . 0 −c3 c2<br />
(B.52)<br />
Note that the scaling coefficients shift by two columns after each pair <strong>of</strong> rows—the factor two being<br />
related to half the approximation coefficients generated at this level compared to the previous—<br />
<strong>and</strong> that the lowest rows <strong>of</strong> the matrix ‘wraparound’ to implement the wraparound within [0, T]<br />
<strong>of</strong> the wavelet <strong>and</strong> scaling functions in the manner described above.<br />
19 In addition, where the number <strong>of</strong> non-zero scaling coefficients K is large, it may not be practical to decompose<br />
entirely to level m = M.<br />
79
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(a)<br />
(c)<br />
(e)<br />
(g)<br />
(i)<br />
s 0 (t)<br />
d 2 (t)<br />
d 4 (t)<br />
d 6 (t)<br />
d 8 (t)<br />
1<br />
0.5<br />
0<br />
−0.5<br />
−1<br />
0 100 200 300 400 500 600 700<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−0.2<br />
−0.4<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−0.2<br />
−0.4<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−0.2<br />
−0.4<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−0.2<br />
−0.4<br />
t<br />
0 100 200 300 400 500 600 700<br />
t<br />
0 100 200 300 400 500 600 700<br />
t<br />
0 100 200 300 400 500 600 700<br />
t<br />
0 100 200 300 400 500 600 700<br />
t<br />
(b)<br />
(d)<br />
(f)<br />
(h)<br />
(j)<br />
d 1 (t)<br />
d 3 (t)<br />
d 5 (t)<br />
d 7 (t)<br />
d 9 (t)<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−0.2<br />
−0.4<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−0.2<br />
−0.4<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−0.2<br />
−0.4<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−0.2<br />
−0.4<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−0.2<br />
−0.4<br />
0 100 200 300 400 500 600 700<br />
t<br />
0 100 200 300 400 500 600 700<br />
t<br />
0 100 200 300 400 500 600 700<br />
t<br />
0 100 200 300 400 500 600 700<br />
t<br />
0 100 200 300 400 500 600 700<br />
Figure 41. Decomposition <strong>of</strong> a signal, s0(t), plotted in (a), into detail signals<br />
d1(t) to d9(t), plotted in (b) to (j), by the pyramid algorithm using the Haar<br />
wavelet.<br />
With this construction, the equation,<br />
bm = Tmsm−1<br />
t<br />
(B.53)<br />
is the equivalent to a combination <strong>of</strong> the compact support <strong>for</strong>m <strong>of</strong> the FWT, equations (B.47)<br />
<strong>and</strong> (B.48). The odd-indexed elements <strong>of</strong> resultant column vector bm are the approximation<br />
coefficients at level m, <strong>and</strong> the even-indexed elements are the detail coefficients. A similar linear<br />
algebra <strong>for</strong>m exists <strong>for</strong> the inverse FWT.<br />
B.6. Wavelet Construction <strong>and</strong> Families. One method <strong>of</strong> constructing wavelet <strong>and</strong> scaling<br />
functions is to begin with the scaling coefficients defined by (B.31) [24].<br />
B.6.1. Conditions on Scaling Coefficients. If equation (B.31) is integrated to give:<br />
∞<br />
−∞<br />
φ(t)dt =<br />
=<br />
∞<br />
−∞<br />
∞<br />
−∞<br />
<br />
ckφ(2t − k)dt<br />
k<br />
<br />
k<br />
80<br />
ckφ(t ′ − k) 1<br />
2 dt′
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
(by change <strong>of</strong> variable: t ′ = 2t)<br />
= 1<br />
2<br />
Since ∞<br />
−∞ φ(t)dt is finite by (B.24), then,<br />
<br />
k<br />
∞<br />
ck<br />
t ′ φ(t<br />
=−∞<br />
′ − k)dt ′<br />
(B.54)<br />
<br />
ck = 2 (B.55)<br />
k<br />
In addition, if the family <strong>of</strong> scaling functions dilated by the same degree m, Φm = {φm,n : n ∈ Z}<br />
are assumed to be an orthonormal basis <strong>of</strong> the subspace Vm, then<br />
<br />
1 if n = n<br />
〈φm,n, φm,n ′〉 =<br />
′<br />
(B.56)<br />
0 otherwise<br />
Without loss <strong>of</strong> generality, assume n to be zero, then from equation (B.31),<br />
<br />
<br />
〈φm,0, φm,n〉 =<br />
(change <strong>of</strong> variables: t ′ = 2t)<br />
k<br />
k<br />
ckφm−1,k(2t) <br />
k ′<br />
k ′<br />
ck ′φm−1,k ′(2(t − n))dt<br />
<br />
<br />
= ckφm−1,k(t ′ ) <br />
ck ′φm−1,k ′(t′ − 2n) 1<br />
2 dt′<br />
= 1<br />
2<br />
<br />
(using φm−1,k ′(t′ − 2n) = φm−1,k ′ +2n(t ′ ))<br />
= 1<br />
2<br />
(change <strong>of</strong> variables: k ′′ = k ′ + 2n)<br />
= 1<br />
2<br />
k<br />
k ′′<br />
<br />
k<br />
k ′′<br />
<br />
k<br />
k ′′<br />
ckck ′<br />
<br />
ckck ′′ −2n<br />
φm−1,k(t<br />
m<br />
′ )φm−1,k ′ +2n(t ′ )dt ′<br />
<br />
φm−1,k(t<br />
m<br />
′ )φm−1,k ′′(t′ )dt ′<br />
ckck ′′ −2n〈φm−1,k, φm−1,k ′′〉 (B.57)<br />
Since the scaling function family Φm−1 = {φm−1,n : n ∈ Z} are an orthonormal basis <strong>of</strong> Vm−1<br />
then:<br />
<br />
1 when k = k<br />
〈φm−1,k, φm−1,k ′′〉 =<br />
′′<br />
0 otherwise<br />
(B.58)<br />
enabling the simplification,<br />
〈φm,0φm,n〉 = 1<br />
2<br />
Thus from (B.56), the condition is [24, 1, 18],<br />
<br />
ckck−2n =<br />
k<br />
<br />
k<br />
ckck−2n<br />
<br />
2 if n = 0<br />
0 otherwise<br />
(B.59)<br />
(B.60)<br />
A third desirable (but not m<strong>and</strong>atory) property is <strong>for</strong> the dilated scaling functions <strong>for</strong>ming the<br />
subspaces Vm to approximate polynomials upto a chosen degree p as closely as possible. From<br />
[24], this condition is:<br />
<br />
k<br />
(−1) k k j ck = 0 <strong>for</strong> j = 0, 1, 2, . . ., p − 1 (B.61)<br />
81
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
This is equivalent to the wavelet function φ(t) having moments <strong>of</strong> 0 up to <strong>and</strong> including the<br />
(p − 1) th moment 20 , i.e.:<br />
<br />
t j φ(t)dt = 0 <strong>for</strong> j = 0, 1, 2, . . ., p − 1 (B.62)<br />
B.6.2. Daubechies Wavelet Family. If the number <strong>of</strong> non-zero coefficients, K is even, using the<br />
two m<strong>and</strong>atory conditions (B.55) <strong>and</strong> (B.60) combined with the ensuring the first K/2 moments<br />
are zero in (B.61), gives rise to a family <strong>of</strong> wavelets called Daubechies Wavelets [18]. Members <strong>of</strong><br />
the family are <strong>of</strong>ten denoted DK where K is the number <strong>of</strong> non-zero scaling coefficients.<br />
The simplest Daubechies wavelet is D2 given by scaling coefficients:<br />
This wavelet is also called the Haar Wavelet.<br />
B.7. <strong>Denoising</strong> <strong>and</strong> Smoothing.<br />
c0 = 1 c1 = 1 (B.63)<br />
B.7.1. <strong>Denoising</strong>. If a full decomposition <strong>of</strong> the discrete-time signal (represented initially as 2 M<br />
approximation coefficients) is per<strong>for</strong>med using the pyramid algorithm, the result is:<br />
s0(t) = sM,0φM,0(t) +<br />
M<br />
m=1<br />
2 M−m −1<br />
n=0<br />
dm,nψm,n(t) (B.64)<br />
If the signal contains noise, with a magnitude less than the original signal itself, then the<br />
signal will give rise to relatively large detail coefficients at particular dilations <strong>and</strong> translations<br />
corresponding to the time locations <strong>and</strong> frequencies <strong>of</strong> the signal, while the noise might be expected<br />
to produce relatively small detail coefficients at different location <strong>and</strong> frequencies. On this basis,<br />
the approach to denoising by wavelets is modify the detail coefficients to minimise the contribution<br />
resulting from the noise.<br />
If each wavelet coefficient is modified to produce d S m,n = dm,n−d N m,n (the superscript S denoting<br />
the signal, <strong>and</strong> N , the noise) then,<br />
s0(t) = sM,0φM,0(t) +<br />
= sM,0φM,0(t) +<br />
M<br />
m=1<br />
M<br />
m=1<br />
2 M−m −1<br />
n=0<br />
2 M−m −1<br />
n=0<br />
S<br />
dm,n + d N <br />
m,n ψm,n(t)<br />
d S m,n ψm,n(t) +<br />
M<br />
m=1<br />
2 M−m −1<br />
n=0<br />
d N m,n ψm,n(t)<br />
= s S 0 (t) + s N 0 (t) (B.65)<br />
where s S 0 (t) is the denoised signal, <strong>and</strong> sN 0<br />
s S 0 (t) = sM,0φM,0(t) +<br />
s N 0<br />
(t) =<br />
M<br />
m=1<br />
2 M−m −1<br />
n=0<br />
(t), the noise, i.e.:<br />
M<br />
m=1<br />
2 M−m −1<br />
n=0<br />
d S m,n ψm,n(t) (B.66)<br />
d N m,n ψm,n(t) (B.67)<br />
Thus, considering the decomposition (B.66), the signal can be reconstructed by per<strong>for</strong>ming the<br />
inverse pyramid algorithm using the amended detail coefficients, d S m,n.<br />
20 The equation <strong>for</strong> j = 0 is derivable from the two conditions (B.55) <strong>and</strong> (B.60)[18], <strong>and</strong> so does not create an<br />
additional constraint on the scaling coefficients.<br />
82
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
B.7.2. Thresholding. There are two major methods <strong>of</strong> amending the detail coefficients to give d S m,n ,<br />
both depending on a threshold value. For generality, the threshold is assumed to be dependent on<br />
the level m, <strong>and</strong> is denoted Λm, but some denoising techniques use the same threshold across all<br />
levels [1].<br />
In hard thresholding, all coefficients with a magnitude less than the threshold are set to zero (ideally<br />
these will correspond to the small noise contribution), while the remainder are left unchanged,<br />
i.e.:<br />
d S m,n =<br />
<br />
0 if |dm,n| < Λm<br />
dm,n otherwise<br />
(B.68)<br />
The other method, s<strong>of</strong>t thresholding, sets coefficients with a magnitude less than the threshold<br />
to zero, as <strong>for</strong> hard thresholding, but subtracts the threshold from the remaining coefficients:<br />
d S m,n =<br />
0 if |dm,n| < Λm<br />
dm,n<br />
|dm,n| (|dm,n| − Λm) otherwise<br />
(B.69)<br />
The reasoning is that noise contributes not only to the small magnitude coefficients consisting <strong>of</strong><br />
just noise, but also to the large magnitude coefficients containing the signal.<br />
One widely used method <strong>of</strong> deriving the threshold is to assume that the noise is Gaussian white<br />
noise. In this case, the expected maximum value in N detail coefficients is given by:<br />
Λ = (2 ln N) 1<br />
2σ (B.70)<br />
where σ is the st<strong>and</strong>ard deviation <strong>of</strong> the noise. At level m, there are 2(M − m) detail coefficients,<br />
thus,<br />
Λm = (2 ln 2 M−m ) 1<br />
2 σ<br />
= (2(M − m)ln 2) 1<br />
2 σ (B.71)<br />
This method is called the universal threshold.<br />
A significant application <strong>of</strong> wavelet denoising is image compression. Although the discrete<br />
signal, representing the image, is not necessarily ‘noisy’, the thresholding method removes small<br />
components in the signal corresponding to the smallest detail coefficients. While this has little<br />
effect on the visual appearance <strong>of</strong> the image, the resulting list <strong>of</strong> detail coefficients contains many<br />
zeros as a result <strong>of</strong> thresholding <strong>and</strong> so can be compressed significantly using st<strong>and</strong>ard algorithms.<br />
To reconstruct the image, the list <strong>of</strong> detail coefficients is uncompressed <strong>and</strong> the image reconstructed<br />
using the inverse pyramid algorithm.<br />
B.7.3. Smoothing. Smoothing is distinguished from denoising in that it considers the frequency (or,<br />
equivalently, scale) <strong>of</strong> the unwanted components <strong>of</strong> the signal, rather than amplitude represented<br />
by the magnitude <strong>of</strong> the detail coefficients.<br />
Starting with a decomposition to level m = m ′ , the signal is represented, from (B.50), as:<br />
s0(t) =<br />
<br />
2 M−m′<br />
−1<br />
n=0<br />
sm ′ ,nφm ′ ,n(t) +<br />
m ′<br />
<br />
m=1<br />
2 M−m −1<br />
n=0<br />
dm,nψm,n(t) (B.72)<br />
The detail coefficients from levels 1 to m relate to dilated wavelets ψm,n(t) with the highest<br />
mean frequencies, the mean frequency reducing by a factor <strong>of</strong> 2 as m increases by 1 (see section<br />
B.1.5). Setting these detail coefficients to zero <strong>and</strong> reconstructing the signal there<strong>for</strong>e produces<br />
an amended signal with the highest frequency components removed, i.e.:<br />
s S 2<br />
0 (t) =<br />
M−m′ −1<br />
n=0<br />
sm ′ ,nφm ′ ,n(t) (B.73)<br />
The removal <strong>of</strong> the high frequency components (at all time locations) results in a signal, s S 0 (t),<br />
that is ‘smoother’ than the original. The higher the level m = m ′ <strong>of</strong> decomposition, the more <strong>of</strong><br />
the lower frequency components are removed, causing increased smoothing.<br />
83
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
B.8. Non-Decimating (Translation Invariant) Trans<strong>for</strong>m. At each stage in the pyramid<br />
algorithm, the number <strong>of</strong> details coefficients produced is half that <strong>of</strong> the previous level. This<br />
is particularly evident in the linear algebra representation <strong>of</strong> the trans<strong>for</strong>m in equation (B.52).<br />
For this reason, the trans<strong>for</strong>m is known as a decimating trans<strong>for</strong>m. However, a consequence <strong>of</strong><br />
this is that, while the original signal can be reconstructed from the set <strong>of</strong> approximation <strong>and</strong><br />
detail coefficients created by decomposition to a given level, as described by equation (B.50), the<br />
representation is not unique.<br />
Considering the a single level <strong>of</strong> decomposition, if the origin from which the translation <strong>of</strong> the<br />
wavelet <strong>and</strong> scaling functions is per<strong>for</strong>med is moved by 1, a different set <strong>of</strong> coefficients are produced:<br />
in effect, the intermediate points in the dyadic grid are being used <strong>for</strong> the decomposition. If the<br />
origin is moved again by 1 in the same direction—a total change <strong>of</strong> 2 units—the original set <strong>of</strong><br />
coefficients are produced again, albeit shifted in location, since the same dyadic grid is being used.<br />
Thus there are two dyadic grids on which the decomposition can be per<strong>for</strong>med at a given level.<br />
An alternative technique is the non-decimating trans<strong>for</strong>m that is invariant under translation by<br />
discrete units. In this trans<strong>for</strong>m, the same number <strong>of</strong> detail coefficients are produced at each level<br />
<strong>of</strong> decomposition by considering both the original decomposition <strong>and</strong> the decomposition shifted<br />
by a discrete unit. If the linear algebra representation is used, the matrix <strong>for</strong> the non-decimating<br />
trans<strong>for</strong>m—the equivalent <strong>of</strong> (B.52)—can be represented by:<br />
⎡<br />
⎤<br />
c0 c1 c2 c3 0 0 0 . . . 0 0 0<br />
⎢−c3<br />
c2 −c1 c0 ⎢<br />
0 0 0 . . . 0 0 0 ⎥<br />
⎢ 0 c0 c1 c2 c3 0 0 . . . 0 0 0 ⎥<br />
⎢ 0 −c3 c2 −c1 c0 0 0 . . . 0 0 0 ⎥<br />
⎢ 0 0 c0 c1 c2 c3 0 . . . 0 0 0 ⎥<br />
T ′<br />
m =<br />
⎢<br />
⎥<br />
⎢ 0 0 −c3 c2 −c1 c0 0 . . . 0 0 0 ⎥<br />
⎢<br />
.<br />
⎢ . . . . . . . ..<br />
⎥<br />
. . . ⎥<br />
⎢ c2 c3 0 0 0 0 0 . . . 0 c0 c1<br />
⎥<br />
⎢<br />
⎢−c1<br />
c0 0 0 0 0 0 . . . 0 −c3 c2<br />
⎥<br />
⎣ c1 c2 c3 0 0 0 0 . . . 0 0 c0 ⎦<br />
c2 −c1 c0 0 0 0 0 . . . 0 0 −c3<br />
(B.74)<br />
Since the trans<strong>for</strong>m considers the two alternative dyadic grids, the total set <strong>of</strong> coefficients<br />
produced is the same <strong>for</strong> any unit translation <strong>and</strong> so the non-decimating trans<strong>for</strong>m is translation<br />
invariant. If a decomposition to m levels is now considered, it can be seen that there are 2 m<br />
choices <strong>for</strong> the dyadic grid on which this decomposition can be per<strong>for</strong>med 21 .<br />
The non-decimating trans<strong>for</strong>m is <strong>of</strong> use in techniques such as denoising <strong>and</strong> smoothing. Since<br />
the set <strong>of</strong> coefficients varies with the choice <strong>of</strong> dyadic grid, the signal resulting from denoising<br />
<strong>and</strong> smoothing using the decimating trans<strong>for</strong>m differs depending on the grid choice. Using the<br />
non-decimating trans<strong>for</strong>m, the denoising or smoothing is applied to each set <strong>of</strong> coefficients (each<br />
set corresponding to one choice <strong>of</strong> grid) <strong>and</strong> the denoised or smoothed signal reconstructed from<br />
each set independently. The resulting set <strong>of</strong> 2 m signals is then averaged to produce the final signal.<br />
This final signal is there<strong>for</strong>e translation invariant: original signals shifted by a integer number <strong>of</strong><br />
discrete units produce the same denoised or smoothed signal.<br />
In practical terms, the non-decimating denoising or smoothing technique minimises artefacts<br />
that can occur when certain features in the signal such as, rapid changes or discontinuities, align<br />
with particular parts <strong>of</strong> the wavelet in the decimating trans<strong>for</strong>m, or when the wavelet is not suitable<br />
<strong>for</strong> approximating the signal[20]. The non-decimating trans<strong>for</strong>m averages out such artefacts over<br />
the 2 m signals.<br />
A useful way <strong>of</strong> calculating the non-decimating trans<strong>for</strong>m to m levels is to per<strong>for</strong>m a st<strong>and</strong>ard<br />
decimating pyramid algorithm on the signal 2 m , but shifting the signal by one discrete unit<br />
on each occasion. This can result in a significant increase in processing time <strong>for</strong> large level <strong>of</strong><br />
signal.<br />
21 There is, <strong>of</strong> course, redundancy in that any <strong>of</strong> the 2 m sets coefficients could be used to reconstruct the original<br />
84
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
decomposition. However, artefacts may still be reduced by using a significantly smaller set subset<br />
<strong>of</strong> the 2 m possible shifts[20].<br />
B.9. Two-Dimensional Discrete Wavelet Trans<strong>for</strong>ms. The techniques <strong>of</strong> discrete wavelet<br />
trans<strong>for</strong>ms can be applied to <strong>2D</strong> signals by the application <strong>of</strong> 1D wavelet <strong>and</strong> scaling functions in<br />
each direction.<br />
If a discrete signal is represented as a function f(x, y) (the variables x <strong>and</strong> y being the equivalent<br />
<strong>of</strong> t in the 1D case), then <strong>2D</strong> equivalent <strong>of</strong> s0(t), the starting point <strong>for</strong> the decomposition given in<br />
(B.44), is given by representing the <strong>2D</strong> signal as the tensor product <strong>of</strong> 1D scaling functions:<br />
s0(x, y) = <br />
s0,(nx,ny)φ0,nx(x)φ0,ny(y) (B.75)<br />
nx<br />
ny<br />
If s 0,(nx,ny)φ0,nx is decomposed into φ1,nx <strong>and</strong> ψ1,nx, then using equations (B.47) <strong>and</strong> (B.48)<br />
<strong>for</strong> compactly supported wavelets,<br />
s0(x, y) = K−1<br />
1 <br />
√<br />
2<br />
nx<br />
ny<br />
nx<br />
ny<br />
kx=0<br />
kx=0<br />
ckxs 0,(2nx+kx,ny)φ1,nx(x)(−1) kx cK−1−kxs 0,(2nx+kx,ny)ψ1,nx(x) φ0,ny(y)<br />
= 1 K−1 <br />
√ ckxφ1,nx(x) + (−1)<br />
2<br />
kx cK−1−kxψ1,nx(x) s0,(2nx+kx,ny)φ0,ny(y) Similarly decomposing s 0,(2nx+kx,ny)φ0,ny(y) gives,<br />
s0(x, y) = 1 √ 2<br />
= 1<br />
2<br />
K−1 <br />
φ1,nx(x) + (−1) kx cK−1−kxψ1,nx(x) <br />
nx<br />
· 1<br />
√ 2<br />
nx<br />
ny<br />
K−1 <br />
ky=0<br />
ny<br />
kx=0<br />
K−1 <br />
nx<br />
(B.76)<br />
ckys 0,(2nx+kx,2ny+ky)φ1,ny(y) + (−1) ky cK−1−ks 0,(2nx+kx,2ny+ky)ψ1,ny(y) <br />
K−1 <br />
kx=0 ky=0<br />
ckxckys 0,(2nx+kx,2ny+ky)φ1,nx(x)φ1,ny(y)<br />
+ (−1) kx cK−1−kxckys 0,(2nx+kx,2ny+ky)ψ1,nx(x)φ1,ny(y)<br />
+ ckx(−1) ky cK−1−ks 0,(2nx+kx,2ny+ky)φ1,nx(x)ψ1,ny(y)<br />
+ (−1) kx cK−1−kx(−1) ky cK−1−ks 0,(2nx+kx,2ny+ky)ψ1,nx(x)ψ1,ny(y) <br />
= <br />
s1,(nx,ny)φ1,nx(x)φ1,ny(y) + d (x)<br />
1,(nx,ny) ψ1,nx(x)φ1,ny(y)<br />
ny<br />
+ d (y)<br />
1,(nx,ny) φ1,nx(x)ψ1,ny(y) + d (xy)<br />
<br />
1,(nx,ny) ψ1,nx(x)ψ1,ny(y)<br />
85<br />
(B.77)
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
where<br />
s 1,(nx,ny) =<br />
K−1 <br />
K−1 <br />
kx=0 ky=0<br />
d (x)<br />
1,(nx,ny) =<br />
K−1 <br />
kx=0 ky=0<br />
d (y)<br />
1,(nx,ny) =<br />
K−1 <br />
ckxckys 0,(2nx+kx,2ny+ky)<br />
K−1 <br />
(−1) kx cK−1−kxckys 0,(2nx+kx,2ny+ky)<br />
K−1 <br />
(−1) ky ckxcK−1−ks0,(2nx+kx,2ny+ky) kx=0 ky=0<br />
d (xy)<br />
1,(nx,ny) =<br />
K−1 <br />
<br />
K−1<br />
(−1) kx+ky cK−1−kxcK−1−ks 0,(2nx+kx,2ny+ky)<br />
kx=0 ky=0<br />
(B.78)<br />
(B.79)<br />
(B.80)<br />
(B.81)<br />
Equations (B.78) to (B.81) represent a single level decomposition in two dimensions. The<br />
summary coefficients, s1,(nx,ny), relate to tensor products <strong>of</strong> scaling functions at the scale <strong>of</strong><br />
the first decomposition level, <strong>and</strong> so the process can be applied iteratively to further levels <strong>of</strong><br />
decomposition. Three sets <strong>of</strong> detail coefficients are produced at each level: d (x)<br />
m,(nx,ny) , d(y)<br />
m,(nx,ny) ,<br />
<strong>and</strong> d (xy)<br />
m,(nx,ny) , relating to the remaining combinations <strong>of</strong> tensor products between the scaling <strong>and</strong><br />
wavelets functions.<br />
Equations (B.76) <strong>and</strong> (B.77) represent a 1D decomposition along the x direction followed by an<br />
equivalent 1D decomposition <strong>of</strong> the resulting coefficients along the y direction, <strong>and</strong> is equivalent to<br />
how the coefficients are derived in practice. Note that equations (B.78) to (B.81) are symmetrical<br />
in x <strong>and</strong> y <strong>and</strong> so the decomposition can also be applied in the y direction followed by the x<br />
direction.<br />
Wavelet techniques, such as denoising <strong>and</strong> smoothing described above, can be applied to the<br />
results <strong>of</strong> the <strong>2D</strong> decomposition with appropriate modifications. For example, the thresholding<br />
<strong>of</strong> detail coefficients may be applied separately to each <strong>of</strong> the three sets <strong>of</strong> detail coefficients.<br />
Similarly, the non-decimating trans<strong>for</strong>m requires shifts <strong>of</strong> the grid in both directions, resulting in<br />
22m shifts <strong>for</strong> a decomposition to m levels.<br />
86
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Appendix C. Genetic Algorithm Overview<br />
This appendix provides an overview <strong>of</strong> evolutionary algorithms, <strong>and</strong> genetic algorithms in particular.<br />
C.1. Evolutionary Algorithms. Evolutionary algorithms (EAs) are a stochastic search technique<br />
used to find solutions to optimisation problems. They are inspired by the biological process<br />
<strong>of</strong> natural selection from which they borrow both some key principles as well as terminology.<br />
Typically EAs operate on a set <strong>of</strong> solutions simultaneously that constitute a ‘population’. The<br />
population is subject to ‘evolutionary pressure’, <strong>of</strong>ten in the <strong>for</strong>m <strong>of</strong> selection <strong>of</strong> the best ‘individuals’<br />
(solutions) in the population to <strong>for</strong>m some or all <strong>of</strong> the next generation <strong>of</strong> the population. In<br />
addition, EAs introduce stochastic variation through two major processes: r<strong>and</strong>om mutation <strong>of</strong><br />
individuals <strong>and</strong> crossover between individuals to produce new members <strong>of</strong> the population (similar<br />
in some respects to biological reproduction). In general, mutation acts to explore new regions <strong>of</strong><br />
the search space, while crossover explores within the region <strong>of</strong> search space that the population<br />
currently occupies. Meanwhile, the evolutionary pressure <strong>of</strong> selection encourages the population<br />
to move towards optimum solutions.<br />
C.2. Steady-State Genetic Algorithms. Genetic Algorithms (GAs) are a widely used type <strong>of</strong><br />
evolutionary algorithm developed in the 1970’s by John Holl<strong>and</strong>[2]. This project uses a variant <strong>of</strong><br />
GA termed Steady-State or Overlapping, the flowchart <strong>of</strong> which is shown in Figure 42.<br />
Initialise Population: The population is usually initialised to a r<strong>and</strong>om set <strong>of</strong> solutions.<br />
Evaluate Fitness (1): The fitness <strong>of</strong> each individual is measured using an objective function<br />
(see below).<br />
Terminate?: The population is tested <strong>and</strong> the algorithm is terminated if a specific condition<br />
is met. Typically this is a requirement that one or more individuals in the population<br />
are sufficiently close to an optimum solution, as measured by their fitness. In practical<br />
Figure 42. Flowchart <strong>of</strong> the Steady-State Genetic Algorithm<br />
87
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
implementations, the algorithm will also be configured to terminate after a set <strong>of</strong> number<br />
<strong>of</strong> generations.<br />
Mutation & Crossover: The individuals in the population are subject to the stochastic<br />
processes <strong>of</strong> mutation (acting on each individual independently) <strong>and</strong> crossover (usually<br />
acting on two individuals). The resulting solutions are potential members <strong>of</strong> the next<br />
generation.<br />
Evaluate Fitness (2): The fitness <strong>of</strong> the new individuals created by mutation <strong>and</strong> crossover<br />
are evaluated.<br />
Derive Next Generation: The members <strong>of</strong> the next generation are selected from the current<br />
generation <strong>and</strong> the new solutions, usually by picking the ‘best’ individuals. In Steady-<br />
State GAs, the selection is constrained so that only some <strong>of</strong> the current generation is<br />
replaced by child solutions. The process continues <strong>for</strong> the next generation from the termination<br />
step.<br />
C.3. Representation. GAs makes a distinction between the genotype, the representation <strong>of</strong> the<br />
solutions, <strong>and</strong> the phenotype, the solution themselves. Traditionally, GAs use a binary string<br />
representation <strong>for</strong> the genome, although this project uses a more complex genotype consisting <strong>of</strong><br />
a variable number <strong>of</strong> real-valued parameters (see section 3.7.1).<br />
C.4. Operators. Operators act to initialise, mutate <strong>and</strong> crossover individuals. Traditional GA<br />
implementations utilise a set <strong>of</strong> mutation <strong>and</strong> crossover operators suitable <strong>for</strong> binary strings. However,<br />
in this project, more complicated custom operators are used owing to the specific genotype<br />
used (see section 3.7).<br />
C.5. Objective Function. The objective (or fitness) function is a measure <strong>of</strong> how good a solution<br />
a particular individual represents. An optimal solution corresponds to the maximum (or minimum)<br />
<strong>of</strong> this function. This project uses a deterministic function described in section 3.7.5, but is also<br />
possible to evaluate fitness by pitting one solution against another in a ‘tournament’ to find the<br />
better solution[2].<br />
88
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Appendix D. Experimental Methods<br />
Sample Solvent: 100% D2O.<br />
Sample Temperature: 300K.<br />
Reference Compound: Internal st<strong>and</strong>ard <strong>of</strong> 1 mM 3-(trimethylsilyl)-propionic acid-d4,<br />
sodium salt (TSP) (0 ppm <strong>for</strong> both F1 <strong>and</strong> F2).<br />
Spectrometer: Bruker ARX 500 <strong>NMR</strong> spectrometer tuned to 1 H signal at 500.13 MHz<br />
( 13 C at 125.76 MHz).<br />
<strong>2D</strong> Phase Program:<br />
• For sucrose/glycine mixtures, <strong>and</strong> the sucrose only spectra, used to illustrate denoising<br />
algorithm <strong>and</strong> peak picking (sections 2 <strong>and</strong> 3); <strong>and</strong> <strong>for</strong> the pea leaf metabolic<br />
spectra: non-gradient phase selective 1 H– 13 C HSQC correlation via double INEPT<br />
transfer.<br />
• For neutral <strong>and</strong> acidic sucrose reference spectra used <strong>for</strong> adaptive binning (section 5);<br />
<strong>and</strong> <strong>for</strong> glucose used as an example <strong>2D</strong> spectra (appendix A): gradient enhanced<br />
phase selective 1 H– 13 C HSQC correlation via double INEPT transfer.<br />
• For all spectra:<br />
– 90 ◦ pulse lengths: 9.2 µs <strong>for</strong> 1 H; 16.5 µs <strong>for</strong> 13 C.<br />
– carbon coupling constant: 145 Hz.<br />
– acquisition was recorded with decoupling <strong>of</strong> 13 C via composite pulse decoupling<br />
(CPD) with a garp sequence.<br />
<strong>Spectra</strong>l Width:<br />
• neutral/acidic sucrose <strong>and</strong> pea: F2 6.666 kHz; F1 22.64 kHz.<br />
• sucrose/glycine mixture: F2 6.666 kHz; F1 20.12 kHz.<br />
Acquisition Data Points:<br />
• pea F2 2048; F1 448.<br />
• neutral/acidic sucrose: F2 1536; F1 480.<br />
• sucrose/glycine mixtures: F2 1536; F1 384.<br />
Window Function: squared-cosine (see section A.6.3).<br />
Baseline Correction: automatic (‘quad’ mode).<br />
Post-Fourier Trans<strong>for</strong>m Data Points: F2 2048; F1 1024 (complex data points in both<br />
directions).<br />
Phase Correction: manual.<br />
89
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
Appendix E. Code Structure<br />
This appendix describes the structure <strong>of</strong> the code used <strong>for</strong> the combined denoising <strong>and</strong> peak<br />
picking code (sections 2, 3 <strong>and</strong> 4), <strong>and</strong> <strong>for</strong> two-dimensional adaptive binning (section 5).<br />
The code is implemented as matlab m-file scripts <strong>and</strong> functions, <strong>and</strong> as MEX files written<br />
in C ++. The source code itself, including additional code not described here, is provided on an<br />
accompanying CD. All m-files <strong>and</strong> MEX files referenced below, <strong>and</strong> those on the CD, were written<br />
specifically <strong>for</strong> this project.<br />
E.1. <strong>Denoising</strong> <strong>and</strong> Peak Picking. The denoising <strong>and</strong> peak picking is implemented as an m-file<br />
script, process spectrum.m. The major m-file functions <strong>and</strong> MEX files called by the script are<br />
shown in Figure 43 <strong>and</strong> described below.<br />
load2dproc: MEX file that loads the real <strong>and</strong> complex spectra directly from Bruker Topspin<br />
data files, returning both as matrices. In addition, it retrieves specific Bruker Topspin<br />
process parameters such as the ppm range covered by the F1 <strong>and</strong> F2 dimensions.<br />
separatenoise.m: Separates the t1-noise from the spectrum, returning the noise <strong>and</strong> remaining<br />
(large) peaks as separate matrices. separatenoisecmplx.m per<strong>for</strong>ms the separation<br />
on the complex spectrum using direct signal thresholding (section 2.5.4). separatenoise1D.m<br />
implements the separation <strong>of</strong> a single 1D trace.<br />
maskt1noise.m: Masks the t1-noise using the algorithm described in section 2.6.<br />
derivecomplexmask.m is used <strong>for</strong> the st<strong>and</strong>ard algorithm, while<br />
Figure 43. Structure <strong>of</strong> denoising <strong>and</strong> peak picking code.<br />
90
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
derivecomplexmaskwavelet.m is used <strong>for</strong> the alternative wavelet-level mask derivation.<br />
(The latter uses functions from the matlab Wavelet Toolbox.)<br />
pickpeaks.m: Finds the peaks in the denoised spectrum <strong>and</strong> identifies both the full <strong>and</strong><br />
thresholded watershed <strong>for</strong> each peak (see section 3.6 <strong>for</strong> an explanation <strong>of</strong> the latter).<br />
Note that this function simply returns a list <strong>of</strong> peaks in the spectrum—identified as local<br />
maxima—rather than per<strong>for</strong>ming the more elaborate peak fitting <strong>of</strong> the genetic algorithm.<br />
identifypeakregions.m: Identifies regions <strong>of</strong> convoluted peaks using the thresholded peak<br />
watersheds.<br />
fitpeakregions.m: Fits each region <strong>of</strong> convoluted peaks to a theoretical peak shape.<br />
calcreferencepeak.m is called once per run <strong>of</strong> the process spectrum.m script to derive<br />
a representation <strong>of</strong> the theoretical peak that enables efficient calculation: see section 3.8.4.<br />
For each region, the MEX file peakfitga is called to run the genetic algorithm. This code<br />
leverages the C ++ GAlib library[25]. To evaluate the fit metric described in section 3.3,<br />
the MEX file calls back to the matlab function peakfitmetric.m.<br />
choosepeak.m: Picks peaks according to fit to theoretical peaks <strong>and</strong>/or peak signal-to-noise<br />
ratio.<br />
integratepeaks.m: Derives the peak intensity by integrating across the peak’s watershed.<br />
derivecleanspct.m: Removes all noise artefacts (including unpicked peaks) from the spectrum<br />
in preparation <strong>for</strong> adaptive binning.<br />
save2dproc: MEX file that optionally saves the denoised spectrum in Bruker Topspin data<br />
file <strong>for</strong>mat.<br />
E.2. Two-Dimensional Adaptive Binning. Adaptive binning is implemented using the script<br />
adaptive binning.m. Functions from the matlab Wavelet Toolkit are used to per<strong>for</strong>m wavelet<br />
smoothing (section 5.3.3). The function derivepeakthreshwatershed.m, shared with the peak<br />
picking code described above, is used to robustly identify bins using watersheds: using a threshold<br />
avoids bin regions that incorrectly incorporate empty (zero intensity) parts <strong>of</strong> the spectrum.<br />
91
<strong>Denoising</strong> <strong>and</strong> <strong>Analysis</strong> <strong>of</strong> <strong>2D</strong> <strong>NMR</strong> <strong>Spectra</strong> <strong>for</strong> <strong>Metabolomic</strong> Pr<strong>of</strong>iling Studies<br />
References<br />
[1] Paul S Addison, The illustrated wavelet trans<strong>for</strong>m h<strong>and</strong>book, Institute <strong>of</strong> Physics Publishing, 2002.<br />
[2] Peter J Bentley, An introduction to evolutionary design by computers, 1st ed., ch. 1, Morgan Kaufmann, 1999.<br />
[3] Joanne T Brindle, Jeremy K Nicholson, Peter M Sch<strong>of</strong>ield, David J Grainger, <strong>and</strong> Elaine Holmes, Application<br />
<strong>of</strong> chemometrics to 1 H <strong>NMR</strong> spectroscopic data to investigate a relationship between human serum metabolic<br />
pr<strong>of</strong>iles <strong>and</strong> hypertension, Analyst 128 (2003), 32–36.<br />
[4] Caroline Brissac, Thérèse E Malliavin, <strong>and</strong> Marc A Delsuc, Use <strong>of</strong> the Cadzow procedure in <strong>2D</strong> <strong>NMR</strong> <strong>for</strong> the<br />
reduction <strong>of</strong> t1 noise, Journal <strong>of</strong> Biomolecular <strong>NMR</strong> 6 (1995), 361–365.<br />
[5] Charles Chiu, An introduction to wavelets, Academic Press, 1992.<br />
[6] Richard A Davis, Adrian J Charlton, John Godward, Mark Harrison, <strong>and</strong> Julie C Wilson, Adaptive binning:<br />
An improved binning method <strong>for</strong> metabolomics data using the undecimated wavelet trans<strong>for</strong>m, submitted to<br />
J. Chemom. Intell. Lab. Syst. as <strong>of</strong> August 2006.<br />
[7] Richard A Davis, Adrian J Charlton, Oehlschlager Sarah, <strong>and</strong> Julie C Wilson, Novel feature selection <strong>for</strong><br />
genetic programming using metabolomic 1 H <strong>NMR</strong> data, J. Chemom. Intell. Lab. Syst. 81 (2006), 50–59.<br />
[8] A P De Weijer, C B Lucasius, L Buydens, <strong>and</strong> G Kateman, Curve fitting using natural computation, Anal.<br />
Chem. 66 (1995), 23–31.<br />
[9] Andrew E Derome, Modern <strong>NMR</strong> techniques <strong>for</strong> chemistry research, Pergamon Press, 1987.<br />
[10] Oliver Fiehn, <strong>Metabolomic</strong>s - the link between genotypes <strong>and</strong> phenotypes, Plant Molecular Biology 48 (2002),<br />
155–171.<br />
[11] Leigh-Anne Fraser, Dulcie A Mulholl<strong>and</strong>, <strong>and</strong> David D Fraser, Classification <strong>of</strong> limonoids <strong>and</strong> protolimonoids<br />
using neural networks, Phytochem. Anal. 8 (1997), 301–311.<br />
[12] Daniel S Garrett, Robert Powers, Angela M Gronenborn, <strong>and</strong> G Marius Clore, A common sense approach<br />
to peak picking in two-, three-, <strong>and</strong> four-dimensional spectra using automatic computer analysis <strong>of</strong> contour<br />
diagrams, J. Magn. Reson. 95 (1991), 214–220.<br />
[13] Andrew Gibbs, Gareth A Morris, Alistair G Swanson, <strong>and</strong> D Cowburm, Suppression <strong>of</strong> t1 noise in <strong>2D</strong> <strong>NMR</strong><br />
spectroscopy by reference deconvolution, J. Magn. Reson. 101 (1993), 351–356.<br />
[14] P J Hore, Nuclear magnetic resonance, Ox<strong>for</strong>d Chemistry Primers, no. 32, Ox<strong>for</strong>d University Press, 1995.<br />
[15] Norman Lloyd Johnson, Samuel Kotz, <strong>and</strong> N Balakrishnan, Continuous univariate distributions, 2nd ed.,<br />
Wiley Series in Probability <strong>and</strong> Mathematical Statistics, vol. 2, John Wiley & Sons, 1994.<br />
[16] The MathWorks, Inc., matlab documentation, version 7.0.4.352 (R14 Service Pack 2) ed., Jan 2005, accessed<br />
as help file documentation.<br />
[17] A F Mehlkopf, D Korbee, Tiggelman T A, <strong>and</strong> Ray Freeman, Sources <strong>of</strong> t1 noise in two-dimensional <strong>NMR</strong>,<br />
J. Magn. Reson. 58 (1984), 315–323.<br />
[18] D E Newl<strong>and</strong>, R<strong>and</strong>om vibrations, spectral <strong>and</strong> wavelet analysis, 3rd ed., Addison Wesley Longman Limited,<br />
1993.<br />
[19] Stephen G Oliver, Michael K Winson, Douglas B Kell, <strong>and</strong> Frank Baganz, Systematic functional analysis <strong>of</strong><br />
the yeast genome, Tibtech 16 (1998), 373–377.<br />
[20] Catherine Perrin, Beata Walczak, <strong>and</strong> Désiré Luc Massart, The use <strong>of</strong> wavelets <strong>for</strong> signal denoising in capillary<br />
electrophoresis, Anal. Chem. 73 (2001), 4903–4917.<br />
[21] William F Reynolds <strong>and</strong> Raul G Enriquez, Gradient-selected versus phase-cycled HMBC <strong>and</strong> HSQC: pros <strong>and</strong><br />
cons, Magn. Reson. Chem. 39 (2001), 531–538.<br />
[22] , Choosing the best pulse sequences, acquisition parameters, postacquisition processing strategies, <strong>and</strong><br />
probes <strong>for</strong> natural product elucidation by <strong>NMR</strong> spectroscopy, J. Nat. Prod. 65 (2002), 221–244.<br />
[23] Shie Qian, Introduction to time-frequency <strong>and</strong> wavelet trans<strong>for</strong>ms, Prentice Hall PTR, 2002.<br />
[24] Gilbert Strang, Wavelets <strong>and</strong> dilation equations: A brief introduction, SIAM Review 31 (1989), no. 4, 614–627.<br />
[25] Matthew Wall, GAlib documentation, Massachusetts Institute <strong>of</strong> Technology, 2.4 ed., 1996, accessed online<br />
(July 2006) <strong>and</strong> as help file documentation.<br />
92