Inverse Trigonometric Functions

Inverse Trigonometric Functions
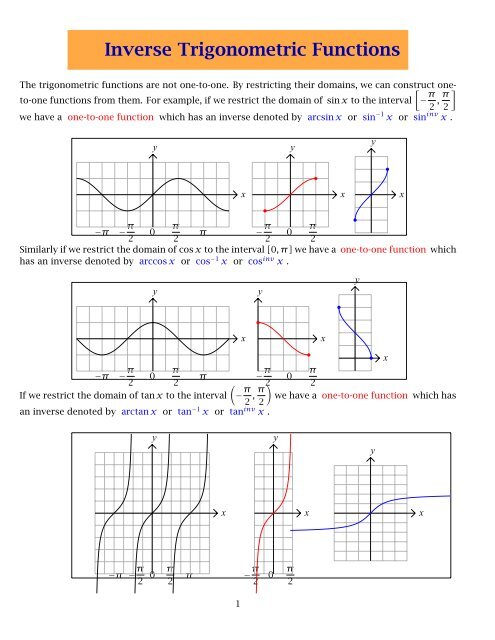
The trigonometric functions are not one-to-one. By restricting their domains, we can construct oneto-one
functions from them. For example, if we restrict the domain of sin x to the interval − π
π
,
2 2
we have a one-to-one function which has an inverse denoted by arcsin x or sin −1 x or sin inv x .
y
−π − π π
0 π −
2 2
π π
0
2 2
Similarly if we restrict the domain of cos x to the interval [0,π]we have a one-to-one function which
has an inverse denoted by arccos x or cos−1 x or cosinv x .
y
−π − π π
0 π −
2 2
π
x
π
0
2 2
If we restrict the domain of tan x to the interval − π
π
, we have a one-to-one function which has
2 2
an inverse denoted by arctan x or tan−1 x or taninv x .
−π − π
2
y
0 π
2
x
x
x
π −π
2
1
y
y
y
0 π
2
x
x
x
y
y
y
x
x

The inverses of the other three trigonometric functions are not often used, but are defined similarly.
We always have the Cancellation Laws, which only hold on the appropriate domains:
sin(sin −1 x) = x, sin −1 (sin x) = x
cos(cos −1 x) = x, cos −1 (cos x) = x
tan(tan −1 x) = x, tan −1 (tan x) = x
sec(sec −1 x) = x, sec −1 (sec x) = x
csc(csc −1 x) = x, csc −1 (csc x) = x
cot(cot −1 x) = x, cot −1 (cot x) = x
Derivatives of Inverse Trigonometric Functions
By differentiating the first Cancellation Law for each trig function, and using trigonometric identities
we get a differentiation rule for its inverse:
For example:
d
dx
sin
sin −1 x
= d(x)
dx
so, by the Chain Rule,
cos sin −1 d
x sin
dx
−1
x = 1 and therefore
d
sin
dx
−1
x =
1
cos sin −1 x
=
1
√ 1 − x 2
(Remember that cos sin −1
x = 1 − sin sin −1 2 x = √ 1 − x2 )
2

We list the standard differentiation rules for the six inverse trig functions. The first three should be
memorized, and the student should practice deriving them all from first principles as done above.
d
sin
dx
−1
x =
1
√ 1 − x 2
d sec−1 x
1
=
dx x √ x2 − 1
d cos−1 x
1
=−√
dx
1 − x2 d csc−1 x
1
=−
dx x √ x2 − 1
d tan−1 x
1
=
dx 1 + x2 d cot−1 x
=−
dx
1
1 + x2 Remember that these formulas are only valid when the domains are as in the definition of the inverse.
Since arcsin x + arccos x ≡ π
, we alternatively get
2
d
d
arccos x = cos
dx dx
−1
x = d
cos
dx
inv 1
x =−√
1 − x2 Also arctan x + arccot x ≡ π
2 gives
d
d
arccot x = cot
dx dx
−1 x
= d
dx
and arcsec x + arccsc x ≡ π
2 gives
d
d
arccsc x = csc
dx dx
−1 x
= d
dx
cot inv
x =− 1
1 + x2
csc inv
x
1
=−
x √ x2 − 1
3

Examples
Example: Problem 4.7-54(p.338 of the
Green Stewart
A painting in an art gallery has height
h and is hung so that its lower edge
is a distance d above the eye of an
observer. How far from the wall should
the observer stand so as to maximize
the angle θ subtended at his eye by the
painting?
Solution 1: (Using Inverse Trig Functions)
Variables:
x = observer’s distance from the wall
α = angle between the horizontal and the bottom of
the painting
θ = angle between the top and bottom of the painting
α
θ
x
Relations:
α = arctan d
x
d + h
θ + α = arctan
x
d + h d
θ(x) = arctan − arctan
x x
We have to find the value of x that will make θ as large as possible, so we differentiate:
1
d + h
−
x2
−
1
− d
x2
=
θ ′ (x) = 2 2 d+h
d
1 +
1 +
x
x
d + h
−
x2 d
2 +
+ (d + h) x2 + d2 =−−(d + h)(x2 + d2
) + d x2 + (d + h) 2
x2 + (d + h) 2
(x2 + d2 )
−dx2 − d3 − hx2 − hd2 + dx2 + d3 + 2d2h + dh2
x2 + (d + h) 2
(x2 + d2 =
)
h(d2 + dh − x2 )
x2 + (d + h) 2
(x2 + d2 ) = 0ifx = d(d + h), which gives a maximum by the First Derivative test.
4
=
h
d

Solution 2: (Not Using Inverse Trig Functions)
We use the same variables, but different relations:
Relations:
tan α = d
x
tan(θ + α) =
Then we have
tan(θ + α) =
d + h
x
tan α + tan θ
1 − tan α tan θ =
d
+ tan θ
x
1 − d
x
x(d + x tan θ) = (h + d)(x − d tan θ) or
xd + x 2 tan θ = (h + d)x − (h + d)d tan θ or
x 2 tan θ + (h + d)d tan θ = (h + d)x − xd or
tan θ x 2
+ (h + d)d = xh or
x
tan θ = h
x2 + (h + d)d
tan θ = d + x tan θ
x − d tan θ
= h + d
x or
We must find the value of x which will make tan θ a maximum. Let f(x) =
tan θ = hf (x)
Then
f ′
x
(x) =
x2 ′
+ (h + d)d
(x 2 + (h + d)d) − x(2x)
(x 2 + (h + d)d) 2
(h + d)d − x 2 = 0orx = (h + d)d
= (h + d)d − x2
= (x2 + (h + d)d)(x) ′ − x(x 2 + (h + d)d) ′
(x 2 + (h + d)d) 2
(x2 = 0if
+ (h + d)d) 2
This value is known as the geometric mean of d and h + d .
5
=
x
x2 , so that
+ (h + d)d

Example: Problem 3.10-32(p.259) of
the green Stewart
A lighthouse is on a small island 3 km
away from the nearest point P on a
straight shoreline and its light makes
four revolutions per minute. How fast θ
is the beam of light moving along the
shoreline when it is 1 km from P? 3
Solution 1: (Using Inverse Trig Functions)
Variables:
x = beam’s distance from P
θ = angle between beam of light and line through the
lighthouse and P
Differentiating, we get
θ ′ 1 x
= 2 1 +
′
3 =
3
9 + x2 x′ ,so
x ′ =
x
3
9 + x2
θ
3
′ 9 + 12
=
3 θ′ = 10
3 θ′ = 10
3
8π = 80
3 π.
Solution 2: (Not Using Inverse Trig Functions)
We use the relation:
tan θ(t) = x(t)
, so differentiation gives
3
sec 2 θ(t)θ ′ (t) = x′ (t)
3 .
We have θ ′ (t) = 4(2π) radians
min
= 8π radians
min ,so
x ′ (t) = 3 sec 2 θ(t)θ ′ (t) = 24π sec 2 θ(t) km
min .
Relations:
θ = arctan x
3
When x = 1, tan θ(t) = 1
3 , and since sec2 α ≡ tan2 α + 1, we have sec2 θ(t) = 1
9
x ′ (t) = 24π 10 km 80π km
km
= = 1600π
9 min 3 min hour .
6
x
P
+ 1 = 10
9 ,so

Example: Problem 4.7-50(p.337) of the
green Stewart
A steel pipe is being carried down a
hallway 9 feet wide. At the end of the
hall there is a right-angled turn into
a narrower hallway 6 feet wide. What
is the length of the longest pipe that
can be carried horizontally around the
corner?
Solution:
θ
A
9
L1
9
B
6
L2
6
θ
C
From the diagram, we have sin θ = 9
, and cos θ =
L1
6
, so that we have L1 =
L2
9
= 9 csc θ and
sin θ
L2 = 6
cos θ = 6 sec θ. Thus we wish to find the minimum value of f(θ) = L1 + L2 = 9 csc θ + 6 sec θ.
we then have f ′ (θ) = 9(− csc θ cot θ) + 6(sec θ tan θ) = 0if
9 csc θ cot θ = 6 sec θ tan θ or 9 1 cos θ
sin θ sin θ
3
2 = sin3 θ
cos 3 θ
3
or
2 = tan3 θ or tan θ = 3
3
2 .
For this value of θ we have csc θ =
so f(θ) = 9
1 +
2
2 3
+ 6 1 +
3
2
3 3
2
1 +
1 sin θ
= 6
cos θ cos θ or
2
2 3
3
≐ 21.07
and sec θ =
7
1 +
3
2
2
3
,