Hyperbolic Functions

Hyperbolic Functions
The trigonometric functions cos α and cos α are defined using the unit circle x2 +y 2 = 1
by measuring the distance α in the counter-clockwise direction along the circumference
of the circle. The area of the sector so determined is α
, so we can equivalently say that
2
cos α and cos α are derived from the unit circle x2 + y 2 = 1 by measuring off a sector
(shaded red )of area α
. The other four trigonometric functions can then be defined in
2
terms of cos and sin.
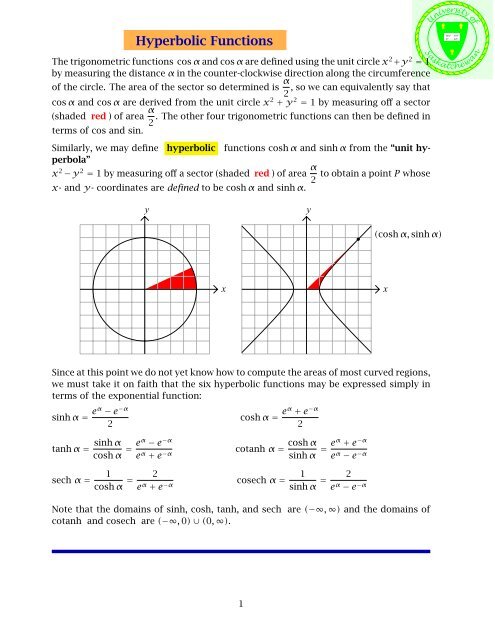
Similarly, we may define hyperbolic functions cosh α and sinh α from the “unit hyperbola”
x2 −y 2 = 1 by measuring off a sector (shaded red )of area α
to obtain a point P whose
2
x- and y- coordinates are defined to be cosh α and sinh α.
y
x
y
(cosh α, sinh α)
Since at this point we do not yet know how to compute the areas of most curved regions,
we must take it on faith that the six hyperbolic functions may be expressed simply in
terms of the exponential function:
sinh α = eα − e−α cosh α =
2
eα + e−α 2
tanh α =
sech α =
sinh α
cosh α = eα − e−α eα + e−α 1
cosh α =
2
e α + e −α
cotanh α =
cosech α =
cosh α
sinh α = eα + e−α eα − e−α 1
sinh α =
2
e α − e −α
Note that the domains of sinh, cosh, tanh, and sech are (−∞, ∞) and the domains of
cotanh and cosech are (−∞, 0) ∪ (0, ∞).
1
x
University of
DEO PAT-
ET RIE
Saskatchewan

α −α e + e
We can check that the point
,
2
eα − e−α
lies on the unit hyperbola:
2
α −α 2 α −α 2 e + e e − e
−
=
2
2
e2α + 2 + e−2α −
4
e2α − 2 + e−2α =
4
4
= 1
4
“Pythagorean” Identities
This gives us the first important hyperbolic function identity:
cosh 2 α − sinh 2 α ≡ 1
This may be used to derive two other identities relating the two other pairs of hyperbolic
functions:
1 − tanh 2 α = sech 2 α and cotanh 2 α − 1 = cosech 2 α
Odd and Even Identities
It is clear that sinh, tanh, cotanh xand cosech are odd functions, while cosh, cotanh ,
and sech are even, so we have the corresponding identities:
sinh(−x) =−sinh x, tanh(−x) =−tanh x,
cotanh (−x) =−cotanh x, cosech (−x) =−cosech x
cosh(−x) = cosh x, sech (−x) = sech x.
Sum and Difference Identities
We can use the above formulas for the hyperbolic functions in terms of e x to derive
analogs of the identities for the trigonometric functions:
sinh α cosh β = eα − e −α
e α+β + e α−β − e −α+β − e −α−β
4
2
sinh β cosh α = eβ − e −β
2
e β + e −β
2
e α + e −α
2
= (eα − e −α )(e β + e −β )
4
= (eβ − e −β )(e α + e −α )
4
2
=
=

e β+α + e β−α − e −β+α − e −β−α
4
Adding these two products gives:
sinh α cosh β + sinh β cosh α =
e α+β + e α−β − e −α+β − e −α−β
4
2e α+β − 2e −α−β
4
= eα+β − e −α−β
2
+ eβ+α + e β−α + e −β+α − e −β−α
4
= e(α+β) − e −(α+β)
2
and subtracting these two products gives:
sinh α cosh β − sinh β cosh α =
e α+β + e α−β − e −α+β − e −α−β
4
2e α−β − 2e −(α−β)
4
Similarly,
cosh α cosh β = eα + e −α
= eα−β − e −(α−β)
2
e α+β + e α−β + e β−α + e −α−β
4
2
sinh α sinh β = eα − e −α
e α+β − e α−β − e β−α + e −α−β
4
2
=
= sinh(α + β)
− eβ+α + e β−α + e −β+α − e −β−α
4
e β + e −β
2
e β − e −β
Adding these two products gives
cosh α cosh β + sinh α sinh β =
e α+β + e α−β + e β−α + e −α−β
4
2
= sinh(α − β)
= (eα + e −α )(e β + e −β )
4
= (eα − e −α )(e β − e −β )
4
+ eα+β − e α−β − e β−α + e −α−β
4
3
=
=
=
=

2e α+β + 2e −α−β
4
= eα+β + e −(α+β)
2
and subtracting them gives:
cosh α cosh β − sinh α sinh β =
e α+β + e α−β + e β−α + e −α−β
4
2e α−β + 2e −α+β
4
= eα−β + e −(α−β)
2
Summarizing, we have four identities:
= cosh(α + β)
− eα+β − e α−β − e β−α + e −α−β
4
= cosh(α − β)
sinh(α + β) ≡ sinh α cosh β + sinh β cosh α
sinh(α − β) ≡ sinh α cosh β − sinh β cosh α
cosh(α + β) ≡ cosh α cosh β + sinh α sinh β
cosh(α − β) ≡ cosh α cosh β − sinh α sinh β
which are almost exactly parallel to those for the trigonometric functions and may be
used to derive sum and difference formulas for the other four hyperbolic functions.
Letting β = α, we get:
sinh 2α ≡ 2 sinh α cosh α,
Double and Half-“Angle” Identities
cosh 2α ≡ cosh 2 α + sinh 2 α ≡ 1 + 2 sinh 2 α ≡ 2 cosh 2 α − 1, so
cosh 2 cosh 2α + 1
α = and sinh
2
2 cosh 2α − 1
α = , and thus:
2
cosh α =
cosh 2α + 1
and sinh α =
2
cosh 2α − 1
2
4
=

cosh α
2 =
cosh α + 1
2
d
d
(sinh x) =
dx dx
d
d
(cosh x) =
dx dx
and sinh α
2 =
cosh α − 1
2
Derivatives
x −x
e − e
2
x −x
e + e
d
d sinh x
(tanh x) = =
dx dx cosh x
cosh x(sinh x) ′ − sinh x(cosh x) ′
cosh 2 x
cosh 2 x − sinh 2 x
cosh 2 x
=
d
d
(cotanh x) =
dx dx
2
= ex − (−e −x )
2
= ex + (−e −x )
2
= cosh x cosh x − sinh x sinh x
1
cosh 2 x = sech 2 x
cosh x
=
sinh x
sinh x(cosh x) ′ − cosh x(sinh x) ′
sinh 2 x
sinh 2 x − cosh 2 x
sinh 2 x
= sinh x sinh x − cosh x cosh x
= −1
sinh 2 x =−cosech 2 x
d
d
(sech x) =
dx dx (cosh x)−1 =
= ex + e −x
2
= ex − e −x
2
= cosh x
= sinh x
cosh 2 x
sinh 2 x
(−1) (cosh x) −2 (cosh x) ′ = (−1) (cosh x) −2 sinh x =−sech x tanh x
d
d
(cosech x) =
dx dx (sinh x)−1 =
5
=
=

(−1) (sinh x) −2 (sinh x) ′ = (−1) (sinh x) −2 cosh x =−cosech xcotanh x
d
(sinh x) = cosh x
dx
d
dx (tanh x) = sech 2 x
d
(sech x) =−sech x tanh x
dx
Summary:
d
(cosh x) = sinh x
dx
d
dx (cotanh x) =−cosech 2 x
d
(cosech x) =−cosech xcotanh x
dx
Graphs ofthe Hyperbolic Functions
y
y = sinh x
y = cosech x
x
y = cosh x
y = sech x
The domains and ranges are summarized in the next table:
6
y
x
y
y = tanh x
y = cotanh x
x

function domain Range
sinh (−∞, ∞) (−∞, ∞)
cosh (−∞, ∞) [1, ∞)
tanh (−∞, ∞) (−1, 1)
cotanh (−∞, 0) ∪ (0, ∞) (−∞, −1) ∪ (1, ∞)
sech (−∞, ∞) (0, 1])
cosech (−∞, 0) ∪ (0, ∞) (−∞, 0) ∪ (0, ∞)
Inverse Hyperbolic Functions
sinh, tanh, cotanh and cosech are one-to-one, but cosh and sech are not. For the
purpose of defining the inverse of cosh and sech we will restrict their domains to
[0, ∞).
We will denote the inverse hyperbolic functions by
sinh −1 , cosh −1 , tanh −1 , cotanh −1 , sech −1 , and cosech −1
or:
sinh inv , cosh inv , tanh inv , cotanh inv , sech inv , and cosech inv
or even:
arcsinh , arccosch , arctanh , arccothh , arcsech , and arccosech .
The usual Cancellation Laws hold in the appropriate domains:
sinh(sinh −1 x) ≡ x sinh −1 (sinh x) ≡ x
cosh(cosh −1 x) ≡ x cosh −1 (cosh x) ≡ x
tanh(tanh −1 x) ≡ x tanh −1 (tanh x) ≡ x
cotanh (cotanh −1 x) ≡ x cotanh −1 (cotanh x) ≡ x
sech (sech −1 x) ≡ x sech −1 (sech x) ≡ x
cosech (cosech −1 x) ≡ x cosech −1 (cosech x) ≡ x
The derivatives of the inverse hyperbolic functions may be found the same way the
derivatives of the inverse trigonometric functions were found: by differentiating the
left-hand Cancellation Laws above:
Example:
Differentiating sinh(sinh −1 x) ≡ x we get
7

cosh(sinh −1
x) sinh −1 ′
x = 1, so
sinh −1 ′ 1
x =
cosh(sinh −1 x) .
Using the identity cosh 2 x − sinh 2 x ≡ 1weget
cosh 2 x ≡ 1 + sinh 2 x,so
cosh x ≡ 1 + sinh 2 x and therefore
cosh(sinh −1 x) =
=
1 + x 2
Thus we have
1 + sinh 2 (sinh −1
x) = 1 + sinh(sinh −1 2 x)
sinh −1 ′
x =
1
√ 1 + x 2
One may similarly derive the derivatives of the other hyperbolic functions:
cosh −1 ′
x =
1
√ x − 1 2
tanh −1 ′
x = cotanh −1 ′
x =
sech −1 ′
x
cosech −1 ′
x =
1
=−
x √ 1 − x2 −1
|x| √ 1 + x 2
1
1 − x 2
Explicit Computation ofInverse Hyperbolics
The inverse hyperbolic functions have the unusual property that they can be explicity
computed:
Example: Solve the equation sinh y = x for y in terms of x.
(The solution will be sinh −1 x!)
We have sinh y = ey − e−y = x, so
2
ey −e−y = 2x or ey −2x −e−y = 0. Multiplying both sides of this equation by e y we get:
8

(e y ) 2 − 2xe y − 1 = 0, a quadratic equation in e y which has solution
e y = −(−2x) ± (−2x) 2 − 4(1)(−1)
2
= 2x ± √ 4x 2 + 4
2
Since x − √ x2 + 1 < 0 and we must have ey > 0, we get
e y
= x + x2 + 1.
Taking logarithms of both sides of this equation, we get
y = ln(x + √ x2 + 1), so we have
sinh −1
x = ln(x + x2 + 1)
= x ± x2 + 1
Similarly,
cosh −1
x = ln(x + x2 − 1) and tanh −1 x = 1
2 ln
1 + x
1 − x
We then have
cosech −1 x = sinh −1 1
x
ln
1
x +
√
1 + x2 |x|
= ln
Similarly
cotanh −1 x = 1
2 ln
x + 1
x − 1
⎛
⎝ 1
x +
2 1
x
⎞ ⎛
+ 1⎠
= ln ⎝ 1
x +
1 + x2 x2 ⎞
⎠ =
and sech −1 √
1 + 1 − x2 x = ln
x
9