Statistical Mechanics - Physics at Oregon State University

More documents

Recommendations

Info

200 CHAPTER 9. GENERAL METHODS: CRITICAL EXPONENTS. approximation, the answers in the Bethe approximation and in mean-field theory will be different. If, on the other hand, the correlation length ξ is much larger than the size of the cluster, the size of the cluster is not important and the problem is essentially solved in a mean-field approach. Since ξ diverges near Tc, the Bethe approximation is equivalent to a mean field theory in this limit. Therefore, the Bethe approximation will give the same critical exponents as mean-field theory. In order to make a real improvement, we need to take into account correlations of infinite range. We can improve the analysis, however. We will use the susceptibility as an example, but the analysis woks for all critical exponents. Near the critical temperature we have χ ≈ A±|T −Tc| γ , plus higher order terms. This means that near the critical temperature we have log(χ) =≈ log(A±) + γ log |T − Tc|. The second term will dominate if we are close enough to the critical temperature. Hence we have log(χ) log |T − Tc| → γ (9.57) near the critical temperature. Hence if we plot the ratio on the left as a function of temperature, we should be able to extract the value of γ. Very simply stated, so what can be wrong. First of all, we assume that we know the value of the critical temperature. That might be true or not. What happens if we are wrong? If we do not use the exact value of the critical temperature a plot of the ratio of the logarithms will show two peaks. The ratio will go to zero when the denominator goes to infinity, or when the temperature reaches the erroneous value of the critical temperature. The ratio will go to infinity when the enumerator diverges, at the true value of the critical temperature. For example, see figure 9.1 where we have used χ = 1 |t−1| (1 + 0.1|t − 1|) and moved Tc by a small amount to Tc = 1.01. We can use this behavior to find the critical temperature. If we have sufficient data near the phase transition we try different values of Tc and see when the peak and zero merge. But what is near the critical temperature? One could guess that the correction in χ is a factor of the form 1 + B±|T − Tc|. This gives an extra term in the denominator equal to the logarithm of this expression, and near the critical temperature we now find log(χ) log |T − Tc| |T − Tc| → γ + B± log |T − Tc| (9.58) The second term goes to zero, indeed. But how fast? We do not know. See figure 9.2 for a typical case. We used the same form as before, but now with the correct value of the critical temperature. In addition, the previous argument assumes that the behavior near the critical temperature is given by powers only. There are theoretical results where near the critical temperature we have logarithmic factors, χ ∝ |T − Tc| γ log |T − Tc|. Because the logarithm goes to infinity slower than any inverse power, such a factor does not change the value of the critical exponent, but it certainly changes the behavior near the phase transition. We
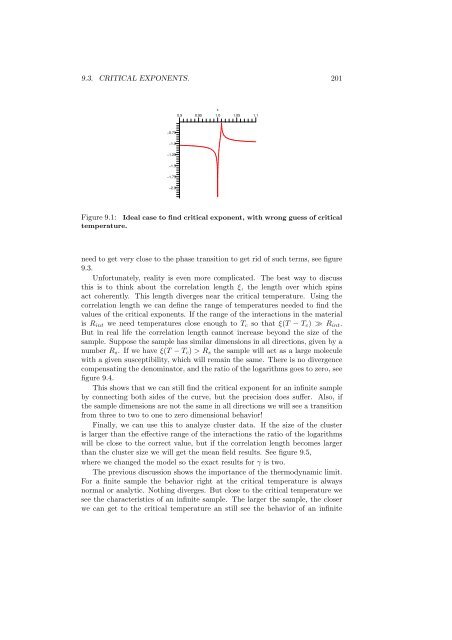
9.3. CRITICAL EXPONENTS. 201 −0.75 −1.0 −1.25 −1.5 −1.75 −2.0 0.9 0.95 Figure 9.1: Ideal case to find critical exponent, with wrong guess of critical temperature. need to get very close to the phase transition to get rid of such terms, see figure 9.3. Unfortunately, reality is even more complicated. The best way to discuss this is to think about the correlation length ξ, the length over which spins act coherently. This length diverges near the critical temperature. Using the correlation length we can define the range of temperatures needed to find the values of the critical exponents. If the range of the interactions in the material is Rint we need temperatures close enough to Tc so that ξ(T − Tc) ≫ Rint. But in real life the correlation length cannot increase beyond the size of the sample. Suppose the sample has similar dimensions in all directions, given by a number Rs. If we have ξ(T − Tc) > Rs the sample will act as a large molecule with a given susceptibility, which will remain the same. There is no divergence compensating the denominator, and the ratio of the logarithms goes to zero, see figure 9.4. This shows that we can still find the critical exponent for an infinite sample by connecting both sides of the curve, but the precision does suffer. Also, if the sample dimensions are not the same in all directions we will see a transition from three to two to one to zero dimensional behavior! Finally, we can use this to analyze cluster data. If the size of the cluster is larger than the effective range of the interactions the ratio of the logarithms will be close to the correct value, but if the correlation length becomes larger than the cluster size we will get the mean field results. See figure 9.5, where we changed the model so the exact results for γ is two. The previous discussion shows the importance of the thermodynamic limit. For a finite sample the behavior right at the critical temperature is always normal or analytic. Nothing diverges. But close to the critical temperature we see the characteristics of an infinite sample. The larger the sample, the closer we can get to the critical temperature an still see the behavior of an infinite x 1.0 1.05 1.1
Page 1:
Statistical Mechanics Henri J.F. Ja
Page 4 and 5:
IV CONTENTS 4.3 Gas of poly-atomic
Page 6 and 7:
VI CONTENTS
Page 8 and 9:
VIII INTRODUCTION Introduction. The
Page 10 and 11:
X INTRODUCTION In chapter nine we d
Page 12 and 13:
2 CHAPTER 1. FOUNDATION OF STATISTI
Page 14 and 15:
Page 16 and 17:
Page 18 and 19:
Page 20 and 21:
10 CHAPTER 1. FOUNDATION OF STATIST
Page 22 and 23:
Page 24 and 25:
Page 26 and 27:
Page 28 and 29:
Page 30 and 31:
Page 32 and 33:
Page 34 and 35:
24 CHAPTER 2. THE CANONICAL ENSEMBL
Page 36 and 37:
Page 38 and 39:
Page 40 and 41:
Page 42 and 43:
Page 44 and 45:
Page 46 and 47:
Page 48 and 49:
Page 50 and 51:
Page 52 and 53:
Page 54 and 55:
44 CHAPTER 3. VARIABLE NUMBER OF PA
Page 56 and 57:
Page 58 and 59:
Page 60 and 61:
Page 62 and 63:
Page 64 and 65:
Page 66 and 67:
Page 68 and 69:
Page 70 and 71:
Page 72 and 73:
Page 74 and 75:
Page 76 and 77:
Page 78 and 79:
68 CHAPTER 4. STATISTICS OF INDEPEN
Page 80 and 81:
Page 82 and 83:
Page 84 and 85:
Page 86 and 87:
Page 88 and 89:
Page 90 and 91:
Page 92 and 93:
Page 94 and 95:
Page 96 and 97:
Page 98 and 99:
Page 100 and 101:
90 CHAPTER 5. FERMIONS AND BOSONS
Page 102 and 103:
92 CHAPTER 5. FERMIONS AND BOSONS t
Page 104 and 105:
94 CHAPTER 5. FERMIONS AND BOSONS w
Page 106 and 107:
96 CHAPTER 5. FERMIONS AND BOSONS T
Page 108 and 109:
98 CHAPTER 5. FERMIONS AND BOSONS S
Page 110 and 111:
Page 112 and 113:
Page 114 and 115:
Page 116 and 117:
Page 118 and 119:
Page 120 and 121:
Page 122 and 123:
Page 124 and 125:
Page 126 and 127:
Page 128 and 129:
Page 130 and 131:
120 CHAPTER 6. DENSITY MATRIX FORMA
Page 132 and 133:
Page 134 and 135:
Page 136 and 137:
Page 138 and 139:
Page 140 and 141:
Page 142 and 143:
Page 144 and 145:
Page 146 and 147:
Page 148 and 149:
Page 150 and 151:
140 CHAPTER 7. CLASSICAL STATISTICA
Page 152 and 153:
Page 154 and 155:
Page 156 and 157:
Page 158 and 159:
Page 160 and 161: 150 CHAPTER 7. CLASSICAL STATISTICA
Page 168 and 169: 158 CHAPTER 8. MEAN FIELD THEORY: C
Page 202 and 203: 192 CHAPTER 9. GENERAL METHODS: CRI
Page 240 and 241: 230 APPENDIX A. SOLUTIONS TO SELECT
Page 260 and 261:
250 APPENDIX A. SOLUTIONS TO SELECT
Page 262 and 263:
Page 264 and 265:
Page 266 and 267:
Page 268 and 269:
Page 270:
show all

Statistical Mechanics - Physics at Oregon State University

Create successful ePaper yourself

Delete template?

Save as template?