WAVES AND VIBRATIONS IN INHOMOGENEOUS STRUCTURES ...

In all the examples shown a density filter is used in
order to avoid checkerboard structures (Guest et al.
2004; Sigmund 2007). The method of moving asymptotes
(Svanberg 1987) is used for the optimization.
6 Examples: vibration response
In this section we show examples of plates optimized
with the objective of minimizing the overall response
given by (41). The structure to be optimized is a simply
supported plate subjected to a harmonic point load in
the center. The plate is 0.5 × 0.5 m, has a thickness of
3 mm and is made from steel and polycarbonate with a
maximum allowed fraction of steel of 25%. There is no
damping included.
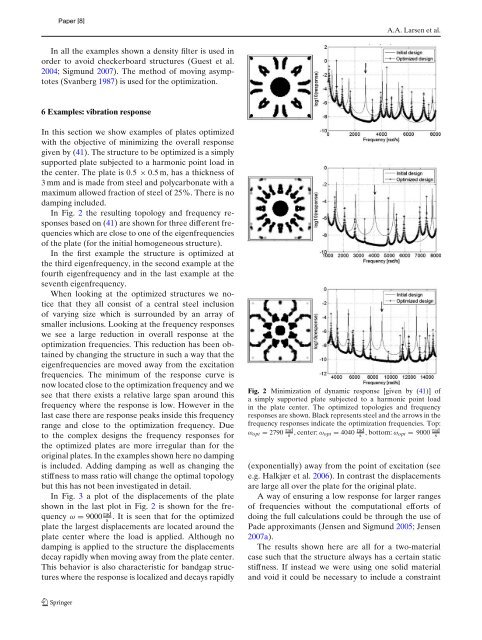
In Fig. 2 the resulting topology and frequency responses
based on (41) are shown for three different frequencies
which are close to one of the eigenfrequencies
of the plate (for the initial homogeneous structure).
In the first example the structure is optimized at
the third eigenfrequency, in the second example at the
fourth eigenfrequency and in the last example at the
seventh eigenfrequency.
When looking at the optimized structures we notice
that they all consist of a central steel inclusion
of varying size which is surrounded by an array of
smaller inclusions. Looking at the frequency responses
we see a large reduction in overall response at the
optimization frequencies. This reduction has been obtained
by changing the structure in such a way that the
eigenfrequencies are moved away from the excitation
frequencies. The minimum of the response curve is
now located close to the optimization frequency and we
see that there exists a relative large span around this
frequency where the response is low. However in the
last case there are response peaks inside this frequency
range and close to the optimization frequency. Due
to the complex designs the frequency responses for
the optimized plates are more irregular than for the
original plates. In the examples shown here no damping
is included. Adding damping as well as changing the
stiffness to mass ratio will change the optimal topology
but this has not been investigated in detail.
In Fig. 3 a plot of the displacements of the plate
shown in the last plot in Fig. 2 is shown for the frequency
ω = 9000 rad
. It is seen that for the optimized
s
plate the largest displacements are located around the
plate center where the load is applied. Although no
damping is applied to the structure the displacements
decay rapidly when moving away from the plate center.
This behavior is also characteristic for bandgap structures
where the response is localized and decays rapidly
A.A. Larsen et al.
Fig. 2 Minimization of dynamic response [given by (41)] of
a simply supported plate subjected to a harmonic point load
in the plate center. The optimized topologies and frequency
responses are shown. Black represents steel and the arrows in the
frequency responses indicate the optimization frequencies. Top:
ωopt = 2790 rad
s ,center:ωopt = 4040 rad
s , bottom: ωopt = 9000 rad
s
(exponentially) away from the point of excitation (see
e.g. Halkjær et al. 2006). In contrast the displacements
are large all over the plate for the original plate.
A way of ensuring a low response for larger ranges
of frequencies without the computational efforts of
doing the full calculations could be through the use of
Pade approximants (Jensen and Sigmund 2005; Jensen
2007a).
The results shown here are all for a two-material
case such that the structure always has a certain static
stiffness. If instead we were using one solid material
and void it could be necessary to include a constraint