WAVES AND VIBRATIONS IN INHOMOGENEOUS STRUCTURES ...

Topological material layout in plates for vibration suppression and wave propagation control
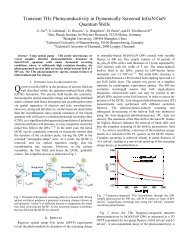
Fig. 1 Plate element showing rotations and translations. Coordinate
system and dimensions
will also be harmonic. We use the following complex
notation
ψx(x, y, t) =ℜ ˜ψx(x, y)e iωt
(6)
ψy(x, y, t) =ℜ ˜ψy(x, y)e iωt
(7)
w(x, y, t) =ℜ iωt
˜w(x, y)e (8)
in which the moments and forces have been written explicitly
in terms of the complex deflection and rotation
amplitudes.
The equations are solved using a standard finite
element method implementation, but first we derive expressions
for energy transport in the plate in continuous
form.
3 Energy flow and the Poynting vector
The Poynting vector P(x, y, z, t) is a measure of the
point-wise instantaneous power flow in the plate. The
in-plane components are (Auld 1973)
Px =−σxx ˙ dx − σyx ˙ dy − σzx ˙ dz
Py =−σxy ˙ dx − σyy ˙ dy − σzy ˙ dz
(12)
(13)
where σij are the stress components and { ˙ dx, ˙ dy, ˙ dz} are
the point-wise velocity components.
The velocity components are related to the plate
model degrees-of-freedom in the following way
˙dx(x, y, z) =−z˙ψx(x, y) (14)
˙dy(x, y, z) =−z ˙ψy(x, y) (15)
˙dz(x, y, z) = ˙w(x, y) (16)
assuming that the out-of-plane (z−direction) velocity
is constant through the plate thickness and the in-plane
velocities depend linearly with the distance z from the
mid-plane (see Fig. 1).
The total xy−plane power flow per unit area, denoted
ˆP(x, y, t), is found by integrating P through the
plate thickness:
ˆP(x, y, t) =
h/2
−h/2
P(x, y, z, t)dz (17)
where a tilde denotes the complex amplitudes and i
is the imaginary unit. ℜ symbolizes the real part of a
complex quantity. Inserting (4)–(8), (1)–(3) canberewritten
in the complex form
D ˜ψx,x + ν ˜ψy,y
,x +
1 − ν
2 D
˜ψx,y + ˜ψy,x
,y
+ kGh ˜w,x − ˜ψx
2 ρh3
+ ω
12 ˜ψx = 0 (9)
D ˜ψy,y + ν ˜ψx,x
,y +
1 − ν
2 D
˜ψy,x + ˜ψx,y
,x
+ kGh ˜w,y − ˜ψy
2 ρh3
+ ω
12 ˜ψy = 0 (10)
kGh ˜w,x − ˜ψx
,x +
kGh ˜w,y − ˜ψy
,y
+ ω 2 so that
ˆPx =
ˆPy =
ρh ˜w = 0 (11)
The integrals can be expressed in terms of the defined
moments and shear forces by using the relations
h/2
h/2
Mx = σxxzdz, My = σyyzdz,
−h/2
−h/2
h/2
Mxy = σyxzdz,
−h/2
h/2
h/2
Tx = σzxdz, Ty = σzydz, (20)
h/2
(σxxz ˙ψx + σyxz ˙ψy − σzx ˙w)dz (18)
−h/2
h/2
(σxyz ˙ψx + σyyz ˙ψy − σzy ˙w)dz (19)
−h/2
−h/2
−h/2
which give the following expressions for the Poynting
vector integrated through the plate thickness
ˆPx = Mx ˙ψx + Mxy ˙ψy − Tx ˙w (21)
ˆPy = Myx ˙ψx + My ˙ψy − Ty ˙w (22)
By inserting the expressions for the moments and
shear forces we obtain
1 − ν
ˆPx =−D(ψx,x + νψy,y) ˙ψx −
2 D(ψx,y + ψy,x) ˙ψy
+ kGh(ψx − w,x) ˙w (23)
1 − ν
ˆPy =−
2 D(ψx,y + ψy,x) ˙ψx − D(νψx,x + ψy,y) ˙ψy
+ kGh(ψy − w,y) ˙w (24)