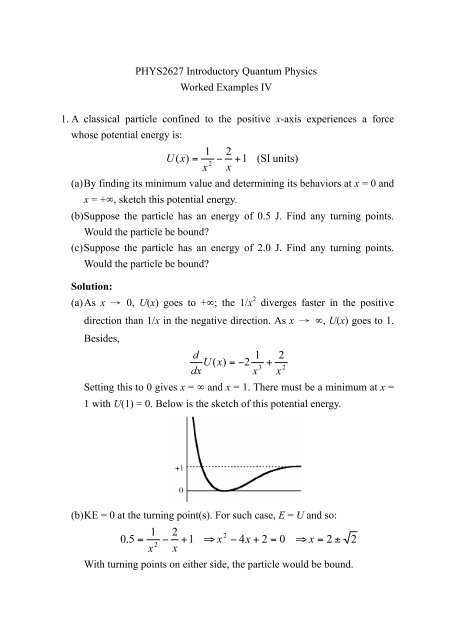
PHYS2627 Introductory Quantum Physics Worked Examples IV 1. A ...

(c) KE = 0 at the turning point(s). For such case, E = U and so:
The only positive root is . There will be a turning point on
only one side. Thus the particle would not be bound.

2. A wave has the form
when x < 0. For x > 0, the wavelength is λ/2. By applying continuity
conditions at x = 0, find the amplitude (in terms of A) and phase of the
wave in the region x > 0. Sketch the wave, showing both x < 0 and x > 0.
Solution:
For x < 0,
For x > 0,
At , ⇒
At , ⇒
Dividing the second of these equations by the first, we obtain
Thus
or

3. The following figure shows the wave function of an electron in a rigid box.
The electron energy is 6.0 eV. How long is this box?
Solution:
The energy levels for a particle in a rigid box are
The wave function shown in the figure corresponds to the n = 3 quantum
state. Thus,

4. Consider a particle moving in a one-dimensional box with walls at x = -L/2
and x = L/2.
(a) Write down the wave functions and probability densities for the states n
= 1, n = 2, and n = 3.
(b) Sketch the wave functions and probability densities. (Hint: Make an
analogy to the case of a particle in a box with walls at x = 0 and x = L.)
Solution:
(a) In the present case, the box is displaced from (0, L) by . Accordingly,
we may obtain the wave functions of our box by replacing x with
L. Using
we get for
in the wave functions of a 1-D box with walls at x = 0 and x =
(b) Below are the wave functions and probability densities for n = 1, 2 and
3.
€
|ψ 1 (x) | 2

5. An electron is trapped at a defect in a crystal. The defect may be modeled
as a one dimensional, rigid-walled box of width 1.00 nm.
(a) Sketch the wave functions and probability densities for the n = 1 and n =
2 states.
(b) For the n = 1 state, find the probability of finding the electron between
x1 = 0.15 nm and x2 = 0.35 nm, where x = 0 is the left side of the box.
(c) Repeat part (b) for the n = 2 state.
(d) Calculate the energies in electron volts for the n = 1 and n = 2 states.
Solution:
(a) The wave functions and probability densities of the n = 1 and n = 2
states are shown below:
(b) Expressing all lengths in units of 10 -10 m, we find
Using the formula , we obtain
(c) Similar to part (b),

(d) Using , we find and .
6. Sketch the n = 8 wave function for the potential energy shown in following
figure.
Solution:
There are three factors to consider. First, the de Broglie wavelength
increases as the particle’s speed and kinetic energy decreases. Thus, the
spacing between the nodes of y(x) increases in regions where U is larger.
Second, a particle is more likely to be found where it is moving the slowest.
Thus, the amplitude of y(x) increases in regions where U is larger. Third,
for n = 8 there will be 8 antinodes to place.
(Note that the wavelength should keep constant in each region of constant
potential.)

7. In most metals, the atomic ions form a regular arrangement called a crystal
lattice. The conduction electrons in the sea of electrons move through this
lattice. Below figure is a one dimensional model of a crystal lattice. The
ions have mass m, charge e, and equilibrium separation b.
(a) Suppose the middle charge is displaced a very small distance (x

(b) The force in part (a) is a linear restoring force of the form F = –kx. This
is Hooke’s law with, in this case, “spring constant” .
The potential energy of the "spring" is
Thus the angular frequency of vibration is
The ground state energy is
Likewise,
.
(c) ΔE between two adjacent levels from part (b) is E2 – E1 = E3 – E2 = E4 –
E3 = 0.0182 eV. The wavelength of a photon with this energy is
The wavelength is in the far infrared region.

8. The wave function
describes a state of the quantum oscillator provided that the constant α is
chosen appropriately.
(a) Using Schrödinger's equation, obtain an expression for α in terms of the
oscillator mass m and the classical frequency of vibration ω. What is the
energy of this state?
(b) What is the quantum number of this state?
(c) Find the normalization constant C.
(Useful formula: for a > 0.)
Solution:
(a) After rearrangement, the Schrödinger equation is
where for a quantum oscillator.
Differentiating gives
and
Therefore, for ψ(x) to be a solution requires
Equating coefficients of like terms gives
and . Thus,
and .

(b) The quantum number is equal to 1 since the energy of the nth state of a
quantum harmonic oscillator is .
(c) The normalization integral is
where the second step follows from the symmetry of the integrand about
x = 0. Identifying a with 2α in the integral
gives