ENTANGLEMENT OF GAUSSIAN STATES Gerardo Adesso
ENTANGLEMENT OF GAUSSIAN STATES Gerardo Adesso ENTANGLEMENT OF GAUSSIAN STATES Gerardo Adesso
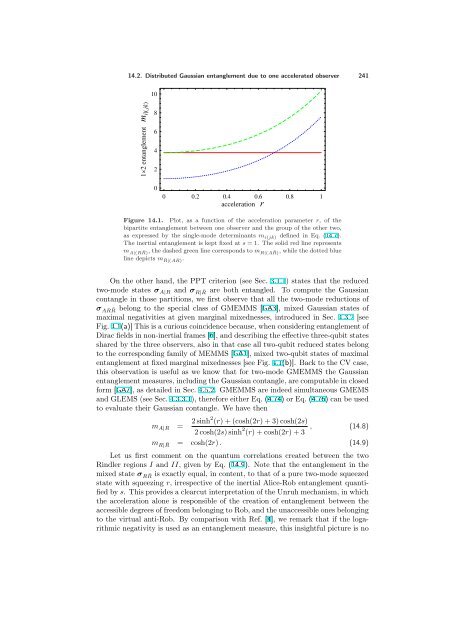
240 14. Gaussian entanglement sharing in non-inertial frames 14.2.1. Bipartite entanglement We now turn to an analysis of the entanglement between the different observers. As already mentioned, we adopt the Gaussian contangle [GA10] (see Sec. 6.1.2.1) as entanglement quantifier. Hence we refer to the notation of Eq. (6.13) and write, for each partition i|j, the corresponding parameter mi|j involved in the optimization problem which defines the Gaussian contangle for bipartite Gaussian states. The Gaussian contangle Gτ (σ p A|R ), which quantifies the bipartite entanglement shared by two Minkowski observers, is equal to 4s2 , as can be straightforwardly found by inserting m p A|R = cosh(2s) in Eq. (6.13). Let us now compute the bipartite entanglement in the various 1 × 1 and 1 × 2 partitions of the state σARR. ¯ The 1 × 2 (Gaussian) contangles are immediately obtained from the determinants of the reduced single-mode states of the globally pure state σARR, ¯ Eq. (14.6), yielding m A|(R ¯ R) = Det σA = cosh(2s) , (14.7) m R|(A ¯ R) = Det σR = cosh(2s) cosh 2 (r) + sinh 2 (r) , m ¯ R|(AR) = Det σ ¯ R = cosh 2 (r) + cosh(2s) sinh 2 (r) . For any nonzero value of the two squeezing parameters s and r (i.e. entanglement in the inertial frame and Rob’s acceleration, respectively), each single party is in an entangled state with the block of the remaining two parties, with respect to all possible global splitting of the modes. This classifies the state σ AR ¯ R as fully inseparable according to the scheme of Sec. 7.1.1 [94]: it contains therefore genuine tripartite entanglement, which will be precisely quantified in the next subsection, thanks to the results of Sec. 7.2.3. Notice also that mA|(RR) ¯ = m p A|R , i.e. all the inertial entanglement is shared, from a non-inertial perspective, between Alice and the group {Rob, anti-Rob}, as expected since the coordinate transformation SρI ,ρII (r) is a local unitary operation with respect to the considered bipartition, which preserves entanglement by definition. In the following, we will always assume s = 0 to rule out trivial circumstances. Interestingly, as already pointed out in Ref. [4], Alice shares no direct entanglement with anti-Rob, because the reduced state σ A| ¯ R is separable by inspection, being Det ε A ¯ R ≥ 0. Actually, we notice that anti-Rob shares the minimum possible bipartite entanglement with the group constituted by Alice and Rob. This follows by recalling that, in any pure three-mode Gaussian state σ123, the local single-mode determinants have to satisfy the triangle inequality (7.22) [GA11], which reads |m1 − m2| + 1 ≤ m3 ≤ m1 + m2 − 1 , with mi ≡ √ Det σi. In our case, identifying mode 1 with Alice, mode 2 with Rob, and mode 3 with anti-Rob, Eq. (14.7) shows that the state σ AR ¯ R saturates the leftmost side of the triangle inequality (7.22), m ¯ R|(AR) = m R|(A ¯ R) − m A|(R ¯ R) + 1 . In other words, the mixedness of anti-Rob’s mode, which is directly related to his entanglement with the other two parties, is the smallest possible one. The values of the entanglement parameters m i|(jk) from Eq. (14.7) are plotted in Fig. 14.1 as a function of the acceleration r, for a fixed degree of initial squeezing s.
14.2. Distributed Gaussian entanglement due to one accelerated observer 241 12 entanglement m i jk 10 8 6 4 2 0 0 0.2 0.4 0.6 0.8 1 acceleration r Figure 14.1. Plot, as a function of the acceleration parameter r, of the bipartite entanglement between one observer and the group of the other two, as expressed by the single-mode determinants m i(jk) defined in Eq. (14.7). The inertial entanglement is kept fixed at s = 1. The solid red line represents m A|(R ¯ R) , the dashed green line corresponds to m R|(A ¯ R) , while the dotted blue line depicts m ¯ R|(AR) . On the other hand, the PPT criterion (see Sec. 3.1.1) states that the reduced two-mode states σ A|R and σ R| ¯ R are both entangled. To compute the Gaussian contangle in those partitions, we first observe that all the two-mode reductions of σ AR ¯ R belong to the special class of GMEMMS [GA3], mixed Gaussian states of maximal negativities at given marginal mixednesses, introduced in Sec. 4.3.2 [see Fig. 4.1(a)] This is a curious coincidence because, when considering entanglement of Dirac fields in non-inertial frames [6], and describing the effective three-qubit states shared by the three observers, also in that case all two-qubit reduced states belong to the corresponding family of MEMMS [GA1], mixed two-qubit states of maximal entanglement at fixed marginal mixednesses [see Fig. 4.1(b)]. Back to the CV case, this observation is useful as we know that for two-mode GMEMMS the Gaussian entanglement measures, including the Gaussian contangle, are computable in closed form [GA7], as detailed in Sec. 4.5.2. GMEMMS are indeed simultaneous GMEMS and GLEMS (see Sec. 4.3.3.1), therefore either Eq. (4.74) or Eq. (4.76) can be used to evaluate their Gaussian contangle. We have then mA|R = 2 sinh2 (r) + (cosh(2r) + 3) cosh(2s) 2 cosh(2s) sinh 2 , (r) + cosh(2r) + 3 (14.8) mR| R ¯ = cosh(2r) . (14.9) Let us first comment on the quantum correlations created between the two Rindler regions I and II, given by Eq. (14.9). Note that the entanglement in the mixed state σ R ¯ R is exactly equal, in content, to that of a pure two-mode squeezed state with squeezing r, irrespective of the inertial Alice-Rob entanglement quantified by s. This provides a clearcut interpretation of the Unruh mechanism, in which the acceleration alone is responsible of the creation of entanglement between the accessible degrees of freedom belonging to Rob, and the unaccessible ones belonging to the virtual anti-Rob. By comparison with Ref. [4], we remark that if the logarithmic negativity is used as an entanglement measure, this insightful picture is no
- Page 203 and 204: 11.2. Generic entanglement and stat
- Page 205 and 206: 11.3. Economical state engineering
- Page 207: Part V Operational interpretation a
- Page 210 and 211: 196 12. Multiparty quantum communic
- Page 212 and 213: 198 12. Multiparty quantum communic
- Page 214 and 215: 200 12. Multiparty quantum communic
- Page 216 and 217: 202 12. Multiparty quantum communic
- Page 218 and 219: 204 12. Multiparty quantum communic
- Page 220 and 221: 206 12. Multiparty quantum communic
- Page 222 and 223: 208 12. Multiparty quantum communic
- Page 224 and 225: 210 12. Multiparty quantum communic
- Page 226 and 227: 212 12. Multiparty quantum communic
- Page 228 and 229: 214 12. Multiparty quantum communic
- Page 230 and 231: 216 12. Multiparty quantum communic
- Page 233 and 234: CHAPTER 13 Entanglement in Gaussian
- Page 235 and 236: 13.1. Gaussian valence bond states
- Page 237 and 238: Eq. (13.3) thus takes the form 13.1
- Page 239 and 240: 13.2. Entanglement distribution in
- Page 241 and 242: s 20 17.5 15 12.5 10 7.5 5 2.5 13.2
- Page 243 and 244: 13.3. Optical implementation of Gau
- Page 245 and 246: of the form Eq. (13.1), with 13.3.
- Page 247 and 248: 13.4. Telecloning with Gaussian val
- Page 249 and 250: CHAPTER 14 Gaussian entanglement sh
- Page 251 and 252: 14.1. Entanglement in non-inertial
- Page 253: 14.2. Distributed Gaussian entangle
- Page 257 and 258: 14.2. Distributed Gaussian entangle
- Page 259 and 260: 6 s 4 14.2. Distributed Gaussian en
- Page 261 and 262: 2.5 0 0 5 10 IΣAR7.5 0 14.3. Distr
- Page 263 and 264: 14.3. Distributed Gaussian entangle
- Page 265 and 266: 0 entanglement condition 14.3. Dist
- Page 267 and 268: 14.3. Distributed Gaussian entangle
- Page 269 and 270: 14.3. Distributed Gaussian entangle
- Page 271 and 272: 4 3 a 2 1 14.4. Discussion and outl
- Page 273: Part VI Closing remarks Entanglemen
- Page 276 and 277: 262 Conclusion and Outlook Gaussian
- Page 278 and 279: 264 Conclusion and Outlook compass
- Page 280 and 281: 266 A. Standard forms of pure Gauss
- Page 282 and 283: 268 A. Standard forms of pure Gauss
- Page 284 and 285: 270 A. Standard forms of pure Gauss
- Page 286 and 287: 272 List of Publications [GA11] G.
- Page 288 and 289: 274 Bibliography [23] C. H. Bennett
- Page 290 and 291: 276 Bibliography [79] J. Eisert, C.
- Page 292 and 293: 278 Bibliography [140] J. Laurat, T
- Page 294 and 295: 280 Bibliography [198] T. Roscilde,
- Page 296: 282 Bibliography [258] J. Von Neuma
14.2. Distributed Gaussian entanglement due to one accelerated observer 241<br />
12 entanglement m i jk<br />
10<br />
8<br />
6<br />
4<br />
2<br />
0<br />
0 0.2 0.4 0.6 0.8 1<br />
acceleration r<br />
Figure 14.1. Plot, as a function of the acceleration parameter r, of the<br />
bipartite entanglement between one observer and the group of the other two,<br />
as expressed by the single-mode determinants m i(jk) defined in Eq. (14.7).<br />
The inertial entanglement is kept fixed at s = 1. The solid red line represents<br />
m A|(R ¯ R) , the dashed green line corresponds to m R|(A ¯ R) , while the dotted blue<br />
line depicts m ¯ R|(AR) .<br />
On the other hand, the PPT criterion (see Sec. 3.1.1) states that the reduced<br />
two-mode states σ A|R and σ R| ¯ R are both entangled. To compute the Gaussian<br />
contangle in those partitions, we first observe that all the two-mode reductions of<br />
σ AR ¯ R belong to the special class of GMEMMS [GA3], mixed Gaussian states of<br />
maximal negativities at given marginal mixednesses, introduced in Sec. 4.3.2 [see<br />
Fig. 4.1(a)] This is a curious coincidence because, when considering entanglement of<br />
Dirac fields in non-inertial frames [6], and describing the effective three-qubit states<br />
shared by the three observers, also in that case all two-qubit reduced states belong<br />
to the corresponding family of MEMMS [GA1], mixed two-qubit states of maximal<br />
entanglement at fixed marginal mixednesses [see Fig. 4.1(b)]. Back to the CV case,<br />
this observation is useful as we know that for two-mode GMEMMS the Gaussian<br />
entanglement measures, including the Gaussian contangle, are computable in closed<br />
form [GA7], as detailed in Sec. 4.5.2. GMEMMS are indeed simultaneous GMEMS<br />
and GLEMS (see Sec. 4.3.3.1), therefore either Eq. (4.74) or Eq. (4.76) can be used<br />
to evaluate their Gaussian contangle. We have then<br />
mA|R = 2 sinh2 (r) + (cosh(2r) + 3) cosh(2s)<br />
2 cosh(2s) sinh 2 ,<br />
(r) + cosh(2r) + 3<br />
(14.8)<br />
mR| R ¯ = cosh(2r) . (14.9)<br />
Let us first comment on the quantum correlations created between the two<br />
Rindler regions I and II, given by Eq. (14.9). Note that the entanglement in the<br />
mixed state σ R ¯ R is exactly equal, in content, to that of a pure two-mode squeezed<br />
state with squeezing r, irrespective of the inertial Alice-Rob entanglement quantified<br />
by s. This provides a clearcut interpretation of the Unruh mechanism, in which<br />
the acceleration alone is responsible of the creation of entanglement between the<br />
accessible degrees of freedom belonging to Rob, and the unaccessible ones belonging<br />
to the virtual anti-Rob. By comparison with Ref. [4], we remark that if the logarithmic<br />
negativity is used as an entanglement measure, this insightful picture is no