ENTANGLEMENT OF GAUSSIAN STATES Gerardo Adesso

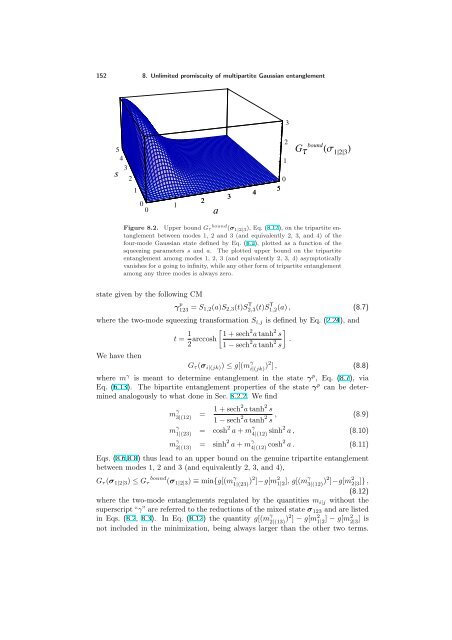
152 8. Unlimited promiscuity of multipartite Gaussian entanglement
5
4
3
s
2
1
0
0
1
2
a
3
4
2
1
0
5
3
GΤ bound Σ 123
Figure 8.2. Upper bound Gτ bound (σ 1|2|3), Eq. (8.12), on the tripartite entanglement
between modes 1, 2 and 3 (and equivalently 2, 3, and 4) of the
four-mode Gaussian state defined by Eq. (8.1), plotted as a function of the
squeezing parameters s and a. The plotted upper bound on the tripartite
entanglement among modes 1, 2, 3 (and equivalently 2, 3, 4) asymptotically
vanishes for a going to infinity, while any other form of tripartite entanglement
among any three modes is always zero.
state given by the following CM
γ p
123 = S1,2(a)S2,3(t)S T 2,3(t)S T 1,2(a) , (8.7)
where the two-mode squeezing transformation Si,j is defined by Eq. (2.24), and
t = 1
2 arccosh
2 2
1 + sech a tanh s
1 − sech 2 a tanh 2
.
s
We have then
Gτ (σi|(jk)) ≤ g[(m γ
i|(jk) )2 ] , (8.8)
where mγ is meant to determine entanglement in the state γp , Eq. (8.7), via
Eq. (6.13). The bipartite entanglement properties of the state γp can be determined
analogously to what done in Sec. 8.2.2. We find
m γ
3|(12) = 1 + sech2a tanh 2 s
1 − sech 2 a tanh 2 ,
s
(8.9)
m γ
1|(23) = cosh2 a + m γ
4|(12) sinh2 a , (8.10)
m γ
2|(13) = sinh2 a + m γ
4|(12) cosh2 a . (8.11)
Eqs. (8.6,8.8) thus lead to an upper bound on the genuine tripartite entanglement
between modes 1, 2 and 3 (and equivalently 2, 3, and 4),
Gτ (σ1|2|3) ≤ Gτ bound (σ1|2|3) ≡ min{g[(m γ
1|(23) )2 ]−g[m 2 1|2 ], g[(mγ 3|(12) )2 ]−g[m 2 2|3 ]} ,
(8.12)
where the two-mode entanglements regulated by the quantities mi|j without the
superscript “γ” are referred to the reductions of the mixed state σ123 and are listed
in Eqs. (8.2, 8.3). In Eq. (8.12) the quantity g[(m γ
2|(13) )2 ] − g[m2 1|2 ] − g[m2 2|3 ] is
not included in the minimization, being always larger than the other two terms.