ENTANGLEMENT OF GAUSSIAN STATES Gerardo Adesso

7.1. Three-mode Gaussian states 125
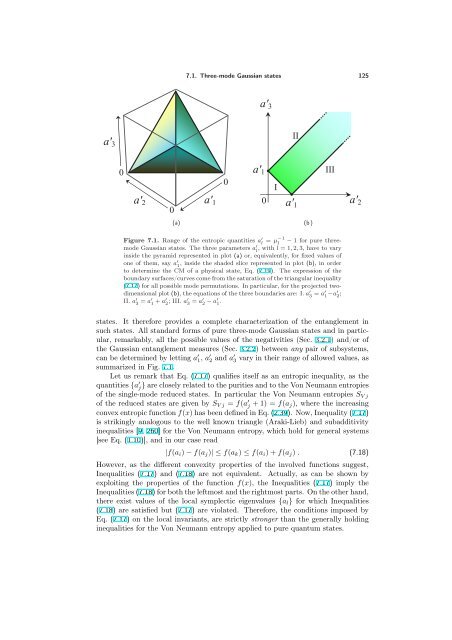
Figure 7.1. Range of the entropic quantities a ′ l = µ−1
l − 1 for pure threemode
Gaussian states. The three parameters a ′ l , with l = 1, 2, 3, have to vary
inside the pyramid represented in plot (a) or, equivalently, for fixed values of
one of them, say a ′ 1 , inside the shaded slice represented in plot (b), in order
to determine the CM of a physical state, Eq. (7.19). The expression of the
boundary surfaces/curves come from the saturation of the triangular inequality
(7.17) for all possible mode permutations. In particular, for the projected twodimensional
plot (b), the equations of the three boundaries are: I. a ′ 3 = a′ 1−a′ 2 ;
II. a ′ 3 = a′ 1 + a′ 2 ; III. a′ 3 = a′ 2 − a′ 1 .
states. It therefore provides a complete characterization of the entanglement in
such states. All standard forms of pure three-mode Gaussian states and in particular,
remarkably, all the possible values of the negativities (Sec. 3.2.1) and/or of
the Gaussian entanglement measures (Sec. 3.2.2) between any pair of subsystems,
can be determined by letting a ′ 1, a ′ 2 and a ′ 3 vary in their range of allowed values, as
summarized in Fig. 7.1.
Let us remark that Eq. (7.17) qualifies itself as an entropic inequality, as the
quantities {a ′ j } are closely related to the purities and to the Von Neumann entropies
of the single-mode reduced states. In particular the Von Neumann entropies SV j
of the reduced states are given by SV j = f(a ′ j + 1) = f(aj), where the increasing
convex entropic function f(x) has been defined in Eq. (2.39). Now, Inequality (7.17)
is strikingly analogous to the well known triangle (Araki-Lieb) and subadditivity
inequalities [9, 260] for the Von Neumann entropy, which hold for general systems
[see Eq. (1.10)], and in our case read
|f(ai) − f(aj)| ≤ f(ak) ≤ f(ai) + f(aj) . (7.18)
However, as the different convexity properties of the involved functions suggest,
Inequalities (7.17) and (7.18) are not equivalent. Actually, as can be shown by
exploiting the properties of the function f(x), the Inequalities (7.17) imply the
Inequalities (7.18) for both the leftmost and the rightmost parts. On the other hand,
there exist values of the local symplectic eigenvalues {al} for which Inequalities
(7.18) are satisfied but (7.17) are violated. Therefore, the conditions imposed by
Eq. (7.17) on the local invariants, are strictly stronger than the generally holding
inequalities for the Von Neumann entropy applied to pure quantum states.