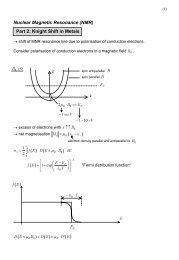
Magnetism 1

Magnetism
Magnetism is a relativistic phenomenon. To understand the origin of the
, one needs to look at moving reference
Lorentz-force F = e⋅ [ E+ v× B]
systems.
A magnetic field is always the consequence of an electric charge in motion!
z
y
r { q
q
v
x
Consider the force between the charges in a reference system S′ that moves
with velocity v along x .
in S′ the charges are at rest!
F ′ = 0
x
1
F ′
y =
4πε
F = 0
z
q
2
2 2
r
Coulomb force
Lorentz-transformation: S′ → S (lab frame)
F = F′
= 0
x x
1
2
−
2
1
⎛ v ⎞
Fy = F ′
y γ =⎜1− 2 ⎟
γ
⎝ c ⎠
F = F′
= 0
z z
2
1
2
2
⎛ v ⎞ 1 q
Fy= ⎜1− ⎟
r = r′
⎝ c ⎠ 4πε
r
2 2
0
2 2 2
⎛ ⎞ ⎛ ⎞ ⎛
v q q
= ⎜1− 2 ⎟γ = γ ⋅q 2 ⎜ 2
⎝ c ⎠ 4πε 0r ⎝4πε 0r qv q
− q
2 2 ⎟= γ ⎜ 2
4πε 0c r ⎠ ⎝4πε
0r
µ 0 qv
− 2
4π
r
1
with 2
c
1
=
εµ
0 0
- 1 -
2
⎞
⎟ ⎠

now for vc γ ≈ 1
⎛ q ⎛−µ 0 ⎞ qv⎞
→Fy≈ q⎜ + v⋅
2 ⎜ ⎟⋅
2 ⎟
⎝4πε 0r
⎝ 4π
⎠ r ⎠
Eel v⋅B
in vector form: v = v ⋅xˆ
2 ⎡ µ 0qv
⎤
= q⎢Eyˆ− ( xˆ zˆ)
2
4π
r
− × ⎥
⎢⎣ yˆ
⎥⎦
(
µ
)
0qv
= q E+ v× B , where Bz=
2
4π
r
→ F = q⋅ (
v× B)
mag
Classical picture
Magnetic moments originate from circular electric currents.
1 ⎛ r ⎞
Biot-Savat: δH = ⋅I⋅ δs
2 ⎜ × ⎟
4π
r ⎝ r ⎠
e
ds
magnetic moment originates from a circular current loop
dµ = I⋅d
S
µ =
dS =
magnetic moment
surface enclosed by the current
2
µ = I dA = 4πr
⋅I
∫
for a circular loop
r
4π
e 2
= r ;
τ
e
I =
τ
for the case of an electron circulating around a ring with period τ
This can be related to the angular momentum of the electron.
le = r× p = r× ve⋅ me 2π
r
where v=
τ
2
2π
r
= me
τ
e
⇒ µ =− ⋅le 2me
relation between angular momentum and magnetic moment of a
circulating electron
They are antiparallel because of the negative charge of the electron.
- 2 -

Of course within an atom the orbit of the electron cannot be described in a
classical way.
⇒ Quantum mechanical description of the hydrogen atom
H
E
0
p
e -
pˆ Ze
= −
m r
2 e
2 2
( ) 2
2 4
mZ e Ze
=− =−
2n 2a
⋅n
o
n
e
2 2 2
0
2
−10
a0=
≈ 0.529× 10
2
me
o o
2
e
1 0
2a0
E − E = = 1 Ry = 13.6 eV
spherical coordinates:
n = 1,2,...
( r, ϑϕ , ) R ( r) Y ( ϑϕ , )
Ψ nlm =
ne
nlm
l = 0,..., n−1
m= - l,..., + l
Laguerre spherical
polynom harmonic
main quantum number
orbital quantum number
magnetic quantum number
n-fold degeneracy of electronic levels
m “Bohr radius”
H ° has sperical symmetry
→Ψ are eigenstates of the orbital angular momentum operator
nlm
lˆ= rˆ× pˆ
Motion in a magnetic field
q
p → ∇− A
i c
H =∇× A
LˆΨ = l( l+
1)
Ψ
nlm nlm
2 2
LˆΨ = l( l+
1)
Ψ
nlm nlm
LˆΨ = mΨ
z nlm nlm
A magnetic vector potential
magnetic field
Recall: A is not uniquely defined: A′ = A+∇χ
→∇× A′ =∇× A+∇×∇
χ
≡0
= H
have to chose transverse gauge where ∇ A = 0
- 3 -
χ: scalar field

Also in general we have to watch out because A and ∇ do not commute.
∇A−A∇≠0
∇A Ψ −A∇ Ψ ≠0
The good thing is, in the transverse gauge they do commute
2 2
⎛ e ⎞ 2 e
e 2
→⎜ ∇+ A⎟ =−∆+ 2 A∇+
A 2
⎝ i c ⎠
i c c
2 2
− e 1 e 2
2 Z⋅e ⇒ H = ∆+ A⋅∇+ A − 2
2me i cme 2me
c r
1
transverse gauge ⇒ A (
= H× r)
2
2 2
−
e 2
⇒ (
)
e
H r (
H r)
Ze
H = ∆+ × ⋅∇+ × −
2
2me i mec 8mc
r
cyclic property (
H× r) ⋅∇= (
r×∇) ⋅H
recognize that r× p = l
op. of angular momentum
r× ∇ = l
i
with the definition
e⋅
= µ B
2m
e
and p
i ∇→
µ = 9.274⋅ 10
B
2 nd term:
µ L⋅H
B
“Bohr magneton”
−24
2
Am
paramagnetic term for orbital magnetism
3 rd term:
assume H zˆ
( 2
) 2 2 2
H× r = H ( x + y ) diamagnetic term
2 2
−
c Ze
= ∆+ B ⋅ + + −
2
2m 8me
r
→ ˆ z
2 2 2
H µ H L H ( x y )
paramagnetic term
diamagnetic term
- 4 -
2

Operator of orbital magnetic momentum:
∂Hˆ
ˆz
ˆ µ orb =− =−µ BL
−
∂H
2
e 2 2 ( x + y ) H
2
4me
Ψnlm z ˆ µ orb Ψnlm 2
e
2 2
=−µ B ⋅m − ⋅H⋅ 2 Ψ nlm x + y Ψnlm
4me
permanent
paramagnetic
moment
Zeeman effect
a) assume Lz = 1, 2 2
x + y
2
2
~ ao; ao
=
me
field-induced diamagnetic moment
2
2 2
2 2 3
Ediam eH 1 x + y
−6
→ ≈ ⋅H ≈10 ⋅H[
Tesla]
2 2 3
E 8mc µ H L 4me
parallel B z
diamagnetic contribution is negligible, only relevant in the absence of a
paramagnetic moment, i.e. for L z = 0 .
b) ratio of paramagnetic term to typical electronic energies:
para
E µ B
= el
E
z
L
2
e
2⋅
a
⋅ H −6
≈210 ⋅ H [ Tesla]
;
2
e
13,6 eV
2a o
=
−5
o
⇒ E ~10 eV ~1K at H = 1Tesla
para
remember: 300K
25meV
1K ≈ˆ
10µ
eV
field dependent term can be treated as weak perturbation with respect to
electronic terms
~> ( ˆ ˆz
o
H 0 + µ BHL ) Ψ nlm = ( En + mH µ B)
Ψnlm
∆E
nlm
H = 0
Z
H > 0
m=2
1
0
-1
-2
∆ E = µ B ⋅H
Zeeman splitting
The magnetic field lifts the degeneracy of the (n,l) shell.
2l+1 sublevels split by ∆ E = µ B ⋅ H
- 5 -
E
for l=2

In addition to the orbital magnetic momentum there is the magnetic momentum
related to the spin of the electron.
→ derived from a fully relativistic treatment!
→ electron has an intrinsic angular momentum with quantization, spin ½ .
2
Sˆχs( s 1)
χ
z
= + χ = spin part of the electron wave function
or
or ,
( ) ( )
nlm r S χ
+ ½
−½ Ψ = Ψ
orbital part
S χ = m
χ m = ± ½
s s
2 2 3 2
S χ = S( S+
1)
χ = χ
4
⇒ additional Zeeman term
para
=− µ ( 2ˆ)
B L+ s H
para
Ψ =+ µ ( m + 2m
) Ψ
B l s
spin part
2 = rel. effect
ms = ± 1/2
Actually the spin is not represented by a vector whose components are scalars
but rather by 2x2 matrices ⇒ the “Pauli-spin” matrices.
⎛0 ˆ σ x = ⎜
⎝1 1⎞ ⎟, 0⎠ ⎛0 σ y = ⎜
⎝i −i
⎞
⎟, 0 ⎠
⎛1 σz = ⎜
⎝0 0 ⎞
⎟,
−1⎠
ˆ σ = ( σx, σ y, σ z)
be a a vector
⎛ a3 ˆ σ ⋅ a =⎜
⎝a1+ ia2 a1−ia2⎞ ⎟
−a3
⎠
such matrices can be multiplied together leading to
2
ˆ σ ⋅ a σb = a⋅ b + iσ a× b and σa
= a show in exercise
( ) ( ) ( ) ( ) 2
The spin angular momentum is determined as
1
sˆ
= ˆ σ
2
⎛0 1⎞ ⎛0 −i
⎞ ⎛1
0 ⎞
Sx = ⎜ ⎟, Sy = ⎜ ⎟, Sz
= ⎜ ⎟
2⎝1 0⎠ 2⎝i0 ⎠ 2⎝0
−1⎠
only Sz
is diagonal
↑z ⎛1⎞ = ⎜ ⎟
⎝0⎠ Sˆ
z ↑z 1
=
2
↑
↓z ⎛0⎞ = ⎜ ⎟
⎝1⎠ ˆ 1
Sz
↓ = −
z ↓
2
ms
- 6 -

The eigenstates concerning spin parallel to x-axis are
↑x =
1 ⎛1⎞ ⎜ ⎟
2 ⎝1⎠ ↓x
=
1
2
⎛ 1 ⎞
⎜ ⎟
⎝−1⎠ ↑y =
1 ⎛1⎞ ⎜ ⎟
2 ⎝i⎠ ↓y
=
1 ⎛ 1 ⎞
⎜ ⎟
2 ⎝−i⎠ ⎛1⎞ ˆ σ x ⎜ ⎟
⎝1⎠ ⎛0 = ⎜
⎝1 1⎞ ⎛1⎞ ⎟ ⎜ ⎟
0⎠ ⎝1⎠ ⎛1⎞ = ⎜ ⎟
⎝1⎠ ⎛ 1 ⎞ ⎛0 ˆ σ x′
⎜ ⎟= ⎜
⎝−1⎠ ⎝1 1⎞ ⎛ 1 ⎞
⎟ ⎜ ⎟
0⎠ ⎝− 1⎠ ⎛−1⎞ = ⎜ ⎟
⎝+ 1⎠ ⎛ 1 ⎞
= ( −1)
⎜ ⎟
⎝− 1⎠
⎛1⎞ ˆ σ y ⎜ ⎟
⎝i⎠ ⎛0 = ⎜
⎝i −i
⎞ ⎛1⎞ ⎟ ⎜ ⎟
0 ⎠ ⎝i⎠ ⎛1⎞ = ⎜ ⎟
⎝i⎠ ⎛ 1 ⎞ ⎛0 σ y ⎜ ⎟ = ⎜
⎝−i⎠ ⎝i −i⎞ ⎛ 1 ⎞
⎟ ⎜ ⎟
0 ⎠ ⎝−i⎠ ⎛−1⎞ = ⎜ ⎟
⎝ i ⎠
⎛1⎞ = ( −1)
⎜ ⎟
⎝i⎠ → This two-component representation of the spin wave functions is known as a
spinor representation. The eigenstates are referred to as spinors.
⎛a⎞ A general spin state can be written as χ = ⎜ ⎟=
a ↑ + b z ↓z
⎝b⎠ 2 2
normalization → a + b = 1
The total angular spin operator is determined as Sˆ ( Sˆ , ˆ , ˆ
x Sy Sz)
vector of 2x2 matrices!
2
→ Sˆ= S
2
+ S
2
+ S
2
( x y z )
( x y z )
2
S χ =
2 2 2
S + S + S
⎛1 1 1⎞ χ = ⎜ + + ⎟
⎝4 4 4⎠ 3
χ = χ
4
2
→ S
3
χ = χ = s( s+ 1)
χ
4
1⎛1 ⎞ 3
⎜ + 1⎟=
2⎝2 ⎠ 4
= . This is a
Commutation relations
⎡Sˆ , ˆ ˆ ˆ ˆ ˆ ˆ
x S ⎤ y = SxSy − SySx = iS
you have to watch out which operator is first
⎣ ⎦
z
applied to the wave function.
ˆ 2
and ⎡⎣S , S ⎤ z ⎦ = 0
The components do not commute with each other; each component commutes
with ˆS
2
.
- 7 -

Raising and lowering operators
The origin of the spin degree of freedom: relativistic energy–momentum
relationship
2 2 2 2 4
E = c p + m c
1
2
−
2
⎛ v ⎞
p= γ ⋅ mv,
γ = ⎜1− 2 ⎟
⎝ c ⎠
∂
E →i, ∂t
p→
∇
i
correspondence principle
4-dimensional covariant form (treat time and space the same way)
P → iδµ
4-dimensional vector
µ
⎛ E ⎞
Pµ = ⎜γmv, ⎟
⎝ c ⎠
⎛ 1 ∂ ⎞
∂ µ = ⎜−∇, c γ t
⎟
⎝ ⎠
→ Klein–Gordon equation:
2 2 4
⎛ ⎞
1 ∂ mc
⎜∆−
− Ψ= 0
2 2 2 ⎟
⎝ c ∂t
⎠
This is a differential equation of the second kind in time and space
∂Ψ
→ the solution requires starting values for Ψ and
γ t
Conclusion: This cannot be!
Dirac’s idea: linearize the equation
2 2
E−c α 0
( ipi − βmc ⎛E c α )
jpj βmc
⎞
⎜
+ +
⎟
i ⎝ j
⎠
this agrees with the Klein–Gordon equation if
α α + α α = 2δij
2
∑ ∑ = i, j ε { x, yz , }
i j j i
αβ+ βa
= 0
i i
relativistic counterpart of
Schrödinger equation
β = 1
cannot be fulfilled with ordinary numbers. Need to consider certain 4x4 matrices.
⎛0 α = ⎜
⎝σ
σ ⎞ ⎛1 ⎟β =
1
⎜
⎠ ⎝0 0⎞ ⎛0 ⎟ with σx = ⎜
1⎠ ⎝1 1⎞ ⎛0 ⎟, σ y = ⎜
0⎠ ⎝i −i
⎞ ⎛1
⎟, σz
= ⎜
0 ⎠ ⎝0
0 ⎞
⎟
−1⎠
2
→ each solution to E∓c 0
( ∑αipi
∓ β mc = is thus also a solution to the Klein–
)
Gordon equation.
→ Dirac’s equation for rel. free particle
⎛ ∂ ⎞
⎜i−cαp−βmc⎟Ψ = 0
⎝ ∂t
⎠
i
- 8 -

The wave function now takes four components:
⎛Ψ1⎞ ⎫
↑
⎜ ⎟ ⎬particle
Ψ2 ⎭
↓
Ψ= ⎜ ⎟
⎜Ψ⎟ 3 ⎫
↑
⎜ ⎟ ⎬anti-particles
Ψ ↓
⎝ 4 ⎠ ⎭
Return to the ordinary Schrödinger equation when the spin is introduced “ad
hoc” as an additional paramagnetic term
→ still need to consider additional velocity effects.
Spin-Orbit-Coupling
⎛r ⎞dφ
Electric field of nucleus E =−∇ φ =−⎜ ⎟ .
⎝r ⎠ dr
As seen by the electron, the nucleus is orbiting around it with velocity v → thus
it creates a magnetic field that acts on the electron spin.
−1
(
H )
nuc = v× E
∂B
2
c
Faraday law: ∇× E =−
γ t
↓
so
∆ E = 2µ
BS⋅Hnuc e1dφ =− S(
v× r) 2
mc r dr
recall (
m v× r) = î
2
e =− 2 2
mc
1 dφ
s⋅l r dr
= spin-orbit-coupling term
This classical estimate is still wrong by a factor of 2.
2
so
⇒ = 2 2
2mc
2
Ze
s⋅l 3
r
H
2
Ze
φ =
r
2
dφZe =−
dr r
→ s and l are no longer decoupled, they are no longer separately conserved
quantities
→ introduce total angular momentum j = l + s
j = l− s , ..., l+ s , 2 j+
1 values
2 2 2 2 2 2
J = L + S + 2SL→ 2SL
= J −L −S
so λ
→ ( 2 2 2
H = J −L −S
)
2
2 2
Ze
λ = 2 2 3
mc r
= spin-orbit-coupling constant
large Z → λ is very large, even larger than the paramagnetic terms in lab fields
for very large Z (heavy elements).
so
∆ E ~1K for Z = 1, but ~ Z
2
- 9 -

( )
0 so Z Z
B µ
H = H + H + J + S H L+ 2 S = J + S since J = L+ S
→ the problem is that s mixes states with different .
ml, ms
l, s⋅ l = i l × s)
, only the Z-components are conserved.
[ ] (
⇒ the spin-orbit interaction lifts the degeneracy between different levels with
s and l (without a magnetic field), it leads to a different kind of splitting than the
Zeeman-splitting → levels with the same j-value are degenerate for some
s , l .
E( J) −E( J − 1) λ
= ( J( J + 1) ) −
2
= λ ⋅J
L( L+ 1) − S( S+ 1) 1
−
2
J −1 J − L L+ 1 − S S+
1
for same
s , l , J = l±½
( ) ( ( ) ( ) ( ) )
- 10 -