Non-dispersive wave packets in periodically driven quantum systems

More documents

Recommendations

Info

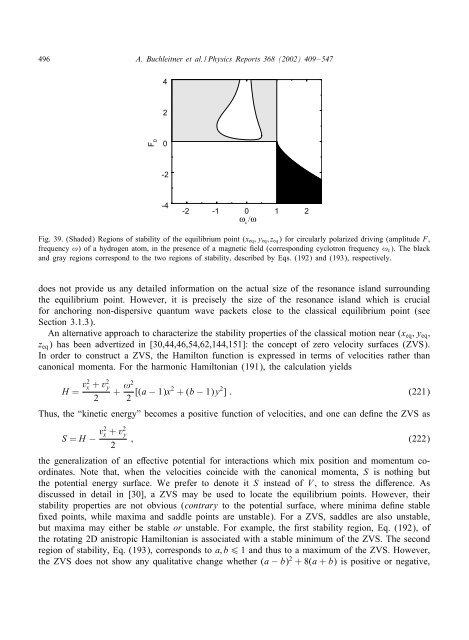
496 A. Buchleitner et al. / Physics Reports 368 (2002) 409–547 F 0 4 2 0 -2 -4 -2 -1 0 1 2 ωc /ω Fig. 39. (Shaded) Regions of stability of the equilibrium point (xeq;yeq;zeq) for circularly polarized driving (amplitude F, frequency !) of a hydrogen atom, in the presence of a magnetic eld (corresponding cyclotron frequency !c). The black and gray regions correspond to the two regions of stability, described by Eqs. (192) and (193), respectively. does not provide us any detailed information on the actual size of the resonance island surrounding the equilibrium point. However, it is precisely the size of the resonance island which is crucial for anchoring non-dispersive quantum wave packets close to the classical equilibrium point (see Section 3.1.3). An alternative approach to characterize the stability properties of the classical motion near (xeq;yeq; zeq) has been advertized in [30,44,46,54,62,144,151]: the concept of zero velocity surfaces (ZVS). In order to construct a ZVS, the Hamilton function is expressed in terms of velocities rather than canonical momenta. For the harmonic Hamiltonian (191), the calculation yields H = v2 x + v2 y !2 + 2 2 [(a − 1)x2 +(b− 1)y 2 ] : (221) Thus, the “kinetic energy” becomes a positive function of velocities, and one can de ne the ZVS as S = H − v2 x + v 2 y 2 ; (222) the generalization of an e ective potential for interactions which mix position and momentum coordinates. Note that, when the velocities coincide with the canonical momenta, S is nothing but the potential energy surface. We prefer to denote it S instead of V , to stress the di erence. As discussed in detail in [30], a ZVS may be used to locate the equilibrium points. However, their stability properties are not obvious (contrary to the potential surface, where minima de ne stable xed points, while maxima and saddle points are unstable). For a ZVS, saddles are also unstable, but maxima may either be stable or unstable. For example, the rst stability region, Eq. (192), of the rotating 2D anistropic Hamiltonian is associated with a stable minimum of the ZVS. The second region of stability, Eq. (193), corresponds to a; b 6 1 and thus to a maximum of the ZVS. However, the ZVS does not show any qualitative change whether (a − b) 2 +8(a + b) is positive or negative,
A. Buchleitner et al. / Physics Reports 368 (2002) 409–547 497 i.e. whether the equilibrium point is stable or unstable. Thus, a ZVS is clearly inappropriate, or at least potentially dangerous, for the discussion of the classical motion close to equilibrium. As a matter of fact, this di culty with the ZVS is crucial in our case, even for the pure CP case, without additional magnetic eld. Indeed, the ZVS becomes 2q +1 S = − x 2 2 q − 1 + 2 y2 ! 2 ; (223) where we use the single parameter q to parametrize S. Atq = 1 (i.e., F = 0, see Eq. (217)), the equilibrium point turns from a saddle (for q¿1) into a maximum. Consequently, the ZVS correctly re ects the change of the equilibrium point from unstable (q¿1) to stable (q¡1). However, for any q ∈ (0; 1), the equilibrium remains a maximum of the ZVS, which completely misses the change of stability at q =8=9. Thus, the very same maximum may change its stability (which fundamentally a ects the classical motion in its vicinity) without being noticed by inspection of the ZVS. The latter evolves very smoothly around q =8=9. Thus, the ZVS contours provide no information on the nature of the classical motion in the vicinity of the equilibrium point, in disaccord with [30,62,44,46,54,144,151]. Similarly, the isovalue contours of the ZVS (which are ellipses in the harmonic approximation) have no relation with the isovalue contours of the ground-state wave packet localized around the equilibrium point (these contours are also ellipses in the harmonic approximation where the wave packet is a Gaussian), contrary to what is stated in [30,44]. For example, the aspect ratio (major axis=minor axis) of the ZVS contour lines is (2q +1)=(1 − q) which varies smoothly around q =8=9, while the aspect ratio of the isocontours of the ground state wave-packet diverges when q → 8=9. 25 Nonwithstanding, a ZVS may be used for other purposes [144], e.g., to show the existence of an ionization threshold for the Hamiltonian (214), when !c ¿! (area coded in black in Fig. 39). Clearly, due to the parabolic con nement in the x–y plane, ionization is only possible along the z direction. The threshold is given by [144] Eion = F 2 =2!(! − !c) ; (224) which lies above the equilibrium energy Eeq. Thus, for parameters in that region, the electron— initially placed close to the stable xed point—cannot ionize. One may expect, therefore, that wave packets built around the equilibrium point for !c ¿! lead to discrete Floquet states. In other cases, e.g., for pure CP driving, non-dispersive wave packets are rather represented by long-living resonances (see Section 7.1). Finally, it has been often argued [30,44,46,54,62,144,151] that the presence of the magnetic eld is absolutely necessary for the construction of non-dispersive wave packets. The authors consider non-dispersive wave packets as equivalent to Gaussian-shaped wave functions (using equivalently the notion of coherent states). Then it is vital that the motion in the vicinity of the xed point is locally harmonic within a region of size ˝. This leads the authors to conclude that non-dispersive wave packets may not exist for the pure CP case except in the extreme semiclassical regime. As opposed to that, the diamagnetic term in Eq. (214) gives a stronger weight to the harmonic term, which is 25 While this argument has been presented here for the simplest case of the harmonic oscillator Hamiltonian (191), it carries over to the full, non-linear model, Eq. (214).
Page 1 and 2:
Abstract Physics Reports 368 (2002)
Page 3 and 4:
A. Buchleitner et al. / Physics Rep
Page 5 and 6:
Page 7 and 8:
Page 9 and 10:
Page 11 and 12:
Page 13 and 14:
Page 15 and 16:
Page 17 and 18:
Page 19 and 20:
Page 21 and 22:
Page 23 and 24:
Page 25 and 26:
Page 27 and 28:
Page 29 and 30:
Page 31 and 32:
Page 33 and 34:
Page 35 and 36:
Page 37 and 38: A. Buchleitner et al. / Physics Rep
Page 43 and 44: → ; → ; A. Buchleitner et al. /
Page 87: A. Buchleitner et al. / Physics Rep
Page 97 and 98: |ψ (z)| 2 |ψ (z)| 2 0.3 0.2 0.1 0
Page 113 and 114: γ /∆ σ/∆ 10 -1 10 -2 10 -3 0.
Page 139:
show all

Non-dispersive wave packets in periodically driven quantum systems

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?