Non-dispersive wave packets in periodically driven quantum systems

More documents

Recommendations

Info

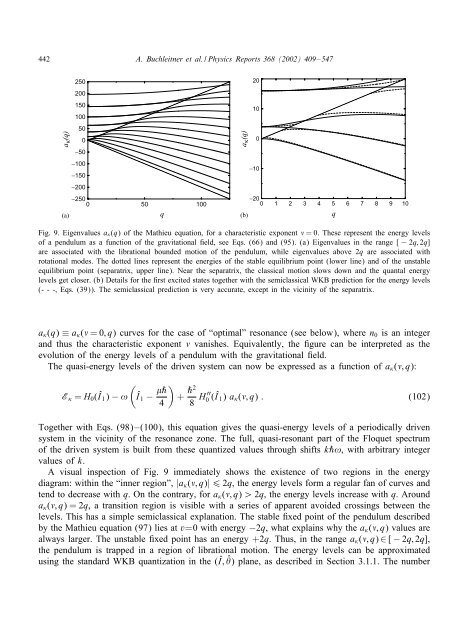
442 A. Buchleitner et al. / Physics Reports 368 (2002) 409–547 a κ(q) 250 200 150 100 50 0 −50 −100 −150 −200 −250 0 50 100 (a) q 20 10 0 −10 −20 0 1 2 3 4 5 6 7 8 9 10 Fig. 9. Eigenvalues a (q) of the Mathieu equation, for a characteristic exponent = 0. These represent the energy levels of a pendulum as a function of the gravitational eld, see Eqs. (66) and (95). (a) Eigenvalues in the range [ − 2q; 2q] are associated with the librational bounded motion of the pendulum, while eigenvalues above 2q are associated with rotational modes. The dotted lines represent the energies of the stable equilibrium point (lower line) and of the unstable equilibrium point (separatrix, upper line). Near the separatrix, the classical motion slows down and the quantal energy levels get closer. (b) Details for the rst excited states together with the semiclassical WKB prediction for the energy levels (- - -, Eqs. (39)). The semiclassical prediction is very accurate, except in the vicinity of the separatrix. a (q) ≡ a ( =0;q) curves for the case of “optimal” resonance (see below), where n0 is an integer and thus the characteristic exponent vanishes. Equivalently, the gure can be interpreted as the evolution of the energy levels of a pendulum with the gravitational eld. The quasi-energy levels of the driven system can now be expressed as a function of a ( ; q): a κ(q) (b) E = H0(Î 1) − ! Î 1 − ˝ + 4 ˝2 ′′ H 0 (Î 1) a ( ; q) : (102) 8 Together with Eqs. (98)–(100), this equation gives the quasi-energy levels of a periodically driven system in the vicinity of the resonance zone. The full, quasi-resonant part of the Floquet spectrum of the driven system is built from these quantized values through shifts k˝!, with arbitrary integer values of k. A visual inspection of Fig. 9 immediately shows the existence of two regions in the energy diagram: within the “inner region”, |a ( ; q)| 6 2q, the energy levels form a regular fan of curves and tend to decrease with q. On the contrary, for a ( ; q) ¿ 2q, the energy levels increase with q. Around a ( ; q)=2q, a transition region is visible with a series of apparent avoided crossings between the levels. This has a simple semiclassical explanation. The stable xed point of the pendulum described by the Mathieu equation (97) lies at v=0 with energy −2q, what explains why the a ( ; q) values are always larger. The unstable xed point has an energy +2q. Thus, in the range a ( ; q) ∈ [ − 2q; 2q], the pendulum is trapped in a region of librational motion. The energy levels can be approximated using the standard WKB quantization in the (Î; ˆ ) plane, as described in Section 3.1.1. The number q
A. Buchleitner et al. / Physics Reports 368 (2002) 409–547 443 of such states is given by Eq. (82) which can be rewritten, using Eq. (100), as Number of trapped states 4 |q| : (103) At the center of the island (states with small a ( ; q) reads [95] and=or large |q|), an approximate expression for a ( ; q) ≈−2|q| +4 + 1 |q| : 2 (104) It does not depend on (what physically means in our case that the states deeply inside the resonance island are insensitive to the boundary condition). When inserted in Eq. (102), it yields exactly the energy levels of Eq. (78), with = N . Hence, the Mathieu approach agrees with the harmonic approximation within the resonance island, for su ciently large islands. For a ( ; q) ¿ 2q, the pendulum undergoes a rotational, unbounded motion, which again can be quantized using WKB. For small |q|, a ( ; q) ≈ 4([( +1)=2]− =2) 2 (where [ ] stands for the integer part), see [95]. With this in Eq. (102), one recovers the known Floquet spectrum, in the limit of a vanishingly weak perturbation. Note, however, that in this rotational mode, the eigenstates are sensitive to the boundary conditions (and the a ( ; q) values depend on ). This is essential for the correct → 0 limit. Around a ( ; q) =2q, the pendulum is close to the separatrix between librational and rotational motion: the period of the classical motion tends to in nity (critical slowing down). That explains the locally enhanced density of states apparent in Fig. 9(a). In Fig. 9(b), we also plot the semiclassical WKB prediction for the quantized a (q) values. Obviously, the agreement with the exact “quantum” Mathieu result is very good, even for weakly excited states, except in the vicinity of the separatrix. This is not unexpected because the semiclassical approximation is known to break down near the unstable xed point, see Sections 2 and 3.1.3 above. The Mathieu equation yields accurate predictions for properties of non-dispersive wave packets in periodically driven quantum systems. Indeed, in the range a ( ; q) ∈ [ − 2q; 2q], the classical motion is trapped inside the resonance island, and the corresponding quantum eigenstates are expected to be non-dispersive wave packets. In particular, the lowest state in the resonance island, associated with the ground state of the pendulum = 0, corresponds to the semiclassical eigenstate N = 0, see Eq. (78), and represents the non-dispersive wave packet with the best localization properties. As can be seen in Fig. 9(b), the semiclassical quantization for this state is in excellent agreement with the exact Mathieu result. This signi es that Eq. (81) can be used for quantitative predictions of the quasi-energy of this eigenstate. As already mentioned, the characteristic exponent does not play a major role inside the resonance island, as the eigenvalues a ( ; q) there depends very little on . However, it is an important parameter outside the resonance, close to the separatrix especially at small q. Indeed, at q = 0, the minimum eigenvalue is obtained for =0 : a0( =0;q= 0) = 0. This implies that, even for very small q, the ground state enters most rapidly the resonance island. On the opposite, the worst case is =1 where the lowest eigenvalue is doubly degenerate: a0( =1;q=0)=a1( =1;q=0)=1. As we are interested in the ground state of the pendulum (the one with maximum localization), the situation for = 0 is preferable: not only the state enters rapidly the resonance island, but it is also separated from the other states by an energy gap and is thus more robust versus any perturbation. We will
Page 1 and 2: Abstract Physics Reports 368 (2002)
Page 3 and 4: A. Buchleitner et al. / Physics Rep
Page 33: A. Buchleitner et al. / Physics Rep
Page 43 and 44: → ; → ; A. Buchleitner et al. /
Page 85 and 86:
A. Buchleitner et al. / Physics Rep
Page 87 and 88:
Page 89 and 90:
Page 91 and 92:
Page 93 and 94:
Page 95 and 96:
Page 97 and 98:
|ψ (z)| 2 |ψ (z)| 2 0.3 0.2 0.1 0
Page 99 and 100:
Page 101 and 102:
Page 103 and 104:
Page 105 and 106:
Page 107 and 108:
Page 109 and 110:
Page 111 and 112:
Page 113 and 114:
γ /∆ σ/∆ 10 -1 10 -2 10 -3 0.
Page 115 and 116:
Page 117 and 118:
Page 119 and 120:
Page 121 and 122:
Page 123 and 124:
Page 125 and 126:
Page 127 and 128:
Page 129 and 130:
Page 131 and 132:
Page 133 and 134:
Page 135 and 136:
Page 137 and 138:
Page 139:
show all

Non-dispersive wave packets in periodically driven quantum systems

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?