Non-dispersive wave packets in periodically driven quantum systems

520 A. Buchleitner et al. / Physics Reports 368 (2002) 409–547
|Shift| Distribution
10 0
10 -1
10 -2
10 -2
10 -1
10 0
10 1
10 -3
(a) |AC Stark Shift| (b)
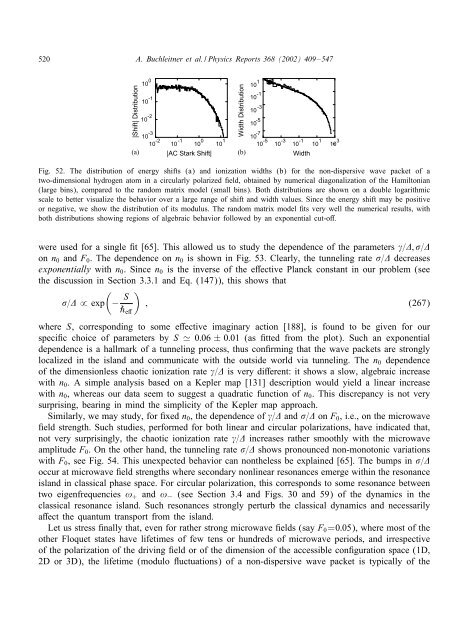
Fig. 52. The distribution of energy shifts (a) and ionization widths (b) for the non-dispersive wave packet of a
two-dimensional hydrogen atom in a circularly polarized eld, obtained by numerical diagonalization of the Hamiltonian
(large bins), compared to the random matrix model (small bins). Both distributions are shown on a double logarithmic
scale to better visualize the behavior over a large range of shift and width values. Since the energy shift may be positive
or negative, we show the distribution of its modulus. The random matrix model ts very well the numerical results, with
both distributions showing regions of algebraic behavior followed by an exponential cut-o .
were used for a single t [65]. This allowed us to study the dependence of the parameters = ; =
on n0 and F0. The dependence on n0 is shown in Fig. 53. Clearly, the tunneling rate = decreases
exponentially with n0. Since n0 is the inverse of the e ective Planck constant in our problem (see
the discussion in Section 3.3.1 and Eq. (147)), this shows that
=
˙ exp − S
˝e
; (267)
where S, corresponding to some e ective imaginary action [188], is found to be given for our
speci c choice of parameters by S 0:06 ± 0:01 (as tted from the plot). Such an exponential
dependence is a hallmark of a tunneling process, thus con rming that the wave packets are strongly
localized in the island and communicate with the outside world via tunneling. The n0 dependence
of the dimensionless chaotic ionization rate = is very di erent: it shows a slow, algebraic increase
with n0. A simple analysis based on a Kepler map [131] description would yield a linear increase
with n0, whereas our data seem to suggest a quadratic function of n0. This discrepancy is not very
surprising, bearing in mind the simplicity of the Kepler map approach.
Similarly, we may study, for xed n0, the dependence of = and = on F0, i.e., on the microwave
eld strength. Such studies, performed for both linear and circular polarizations, have indicated that,
not very surprisingly, the chaotic ionization rate = increases rather smoothly with the microwave
amplitude F0. On the other hand, the tunneling rate = shows pronounced non-monotonic variations
with F0, see Fig. 54. This unexpected behavior can nontheless be explained [65]. The bumps in =
occur at microwave eld strengths where secondary nonlinear resonances emerge within the resonance
island in classical phase space. For circular polarization, this corresponds to some resonance between
two eigenfrequencies !+ and !− (see Section 3.4 and Figs. 30 and 59) of the dynamics in the
classical resonance island. Such resonances strongly perturb the classical dynamics and necessarily
a ect the quantum transport from the island.
Let us stress nally that, even for rather strong microwave elds (say F0=0:05), where most of the
other Floquet states have lifetimes of few tens or hundreds of microwave periods, and irrespective
of the polarization of the driving eld or of the dimension of the accessible con guration space (1D,
2D or 3D), the lifetime (modulo uctuations) of a non-dispersive wave packet is typically of the
Width Distribution
10 1
10 -1
10 -3
10 -5
10 -7
10 -5
10 -3
10 -1
Width
10 1
10 3