Math 411: Honours Complex Variables - University of Alberta

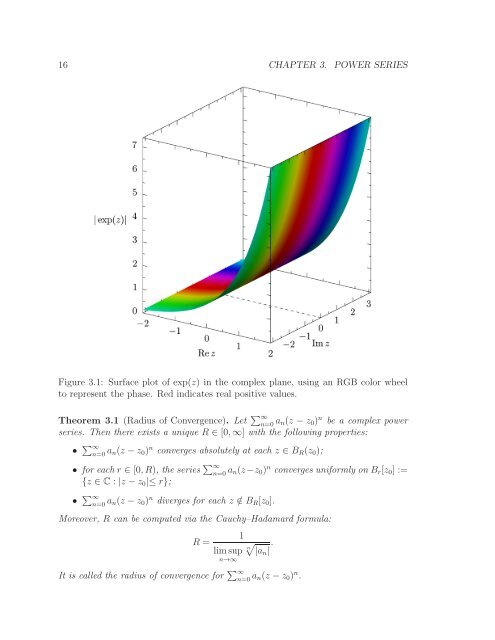
16 CHAPTER 3. POWER SERIES
Figure 3.1: Surface plot of exp(z) in the complex plane, using an RGB color wheel
to represent the phase. Red indicates real positive values.
Theorem 3.1 (Radius of Convergence). Let � ∞
n=0 an(z − z0) n be a complex power
series. Then there exists a unique R ∈ [0,∞] with the following properties:
• � ∞
n=0 an(z −z0) n converges absolutely at each z ∈ BR(z0);
• for each r ∈ [0,R), the series � ∞
n=0 an(z−z0) n converges uniformly on Br[z0] :=
{z ∈ C : |z −z0|≤ r};
• � ∞
n=0 an(z −z0) n diverges for each z /∈ BR[z0].
Moreover, R can be computed via the Cauchy–Hadamard formula:
R =
1
�
n
limsup |an|
n→∞
.
It is called the radius of convergence for � ∞
n=0 an(z −z0) n .