Partikel- und Schüttgutmechanik - Lehrstuhl Mechanische ...

3 Einführung in die Partikel- und Schüttgutmechanik 13 

3.1 Partikelmechanik und Partikelhaftkräfte in Schüttgütern 14 

3.1.1 Molekulare Wechselwirkungen und Partikelhaftkräfte 14 

3.1.2 Übersicht über wesentliche Partikelhaftkräfte in Schüttgütern14 

3.1.3 Mechanik eines weichen adhäsiven Partikelkontaktes 18 

3.1.3.1 Normalkraft-Weg-Beziehungen 18 

3.1.3.2 Tangentialkraft-Weg-Beziehungen 19 

3.1.3.3 Rollmoment-Rollwinkel-Beziehungen 19 

3.1.3.4 Torsionsmoment-Drehwinkel-Beziehungen 19 

3.1.3.5 Vergleich der charakt. Haft- und Reibungsgrenzen 19 

3.1.3.6 Hysterese-, Ablöse- & Reibungsarbeit des lastabhängigen 

Partikelkontaktes 20 

3.1.3.7 Weicher adhäsiver Partikelkontakt in Wasser 20 

3.1.3.8 Festkörperbrückenbindungen im Partikelkontakt 20 

3.1.4 Messung der Kontaktkräfte 20 

3.1.5 Modelle bimodaler kubischer Partikelpackungen 21 

3.1.6 Mikro-Makro-Übergang in einer bewegten Partikelpackung21 

3.1.7 Einführung in die Diskrete-Elemente-Methode (DEM) 21 

3.2 Kontinuumsmechanische Grundlagen des Fließverhaltens vorverdichteter 

Partikelpackungen 22 

3.2.1 Zweiachsiger Spannungszustand 22 

3.2.2 Kontinuumsmechanische Fließkriterien (Bruchhypothesen) 27 

3.2.3 Partikelmechanisch begründete Fließkriterien 32 

3.2.4 Partikelmechanische Pulvereigenschaften & Fließkennwerte36 

3.2.5 Kompressionsfunktionen, Schüttgut- und Packungsdichte 43 

3.3 Messung der Fließeigenschaften von Schüttgütern 49 

3.3.1 Übersicht der Meßgeräte 49 

3.3.2 Meßmethodik eines direkten Scherversuches 50 

3.3.3 Numerische Versuchsauswertung 53 

3.3.4 Anscherarbeit 53 

3.4 Fließkennwerte kohäsiver Schüttgüter und deren Beeinflussung 53 

3.4.1 Wesentliche Fließkennwerte kohäsiver Pulver 53 

3.4.2 Übersicht des mechanischen Verhaltens kohäsiver Pulver 54 

3.4.3 Tabelle mit „Datenblatt Schüttgutkennwerte“ 55 

3.5 Durchströmungs-, Fluidisier- und Entlüftungsverhalten 56 

3.5.1 Durchströmungsverhalten von Partikelschichten 56 

3.5.2 Durchströmung von Wirbelschichten 63 

3.5.3 Entlüftungsverhalten 74 

3.6 Feldgleichungen des ebenen Spannungszustandes 86 

Schüttec_3 VO Partikelmechanik und Schüttguttechnik, Kontakt- und Kontinuumsmechanik 

Prof. Dr. Jürgen Tomas, 16.04.2012 

12

3 Einführung in die Partikel- und Schüttgutmechanik 

• Gliederung Folie F 3.1 

• Übersicht über die Eigenschaftsfunktionen, Prozess- und Handha- 

bungsprobleme kohäsiver Pulver: Folie F 3.2 

• Multiskalige Modellierung der Dynamik einer Partikelpackung: 

− Flüssigkeit 

• zur Beschreibung des Fließverhaltens Angabe der 

− Festkörper 



Folie F 3.3 

Viskosität = f (Temperatur, Zusammensetzung) meist ausreichend 

∗ horizontale Oberfläche 

p 

∗ keine Zugfestigkeit 

∗ iso- oder hydrostatischer 

Druck: 

pv h l 

= p = ρ ⋅ g ⋅ H ( 3.1) 

Bild 3.1: Flüssigkeitsdrücke = f(H) 

• zur Beschreibung des Festigkeitsverhaltens, gewöhnlich Druck- u. 

Zugfestigkeit, und des elastischen Deformationsverhaltens, E-Modul 

notwendig 

∗ beliebige Oberfläche möglich 

∗ = m ⋅ g / A ( 3.2) 

p v 

∗ ohne Deformation ph = 0 

∗ hohe Zugfestigkeit 

− Schüttgut 

H 

pw 

H 

α 

pv 

Bild 3.2: Festkörperdrücke 

Bild 3.3: Schüttgutdrücke = f(H) 

• charakteristische Höhenverteilung des Vertikaldruckes pv, des Horizontaldruckes 

ph und des Wandreibungsdruckes pw (Wandschubspannung), 

daher 

∗ kegelförmig aufgeschüttete Oberfläche möglich, sog Schüttkegel 

∗ geringe aber vorhandene Zugfestigkeit (siehe Abschn. Haftkräfte) 

ph 

pv 

ph 

H 

H 

pv ph 

pw ph pv 

p 

13

• Zur Beschreibung des Fließverhaltens eine Anzahl von Kennwerten 

= f (Partikelgröße, Feuchte, Lagerzeit ...) notwendig 

• sog. "4. Aggregatzustand" mit Übergänge zum Verhalten von Fest- 

körpern bei Zeitverfestigungen bzw. Flüssigkeiten bei Flüssigkeits- 

sättigung oder Wirbelschichtfluidisierung 

• komplizierteste Fall zur Formulierung ihrer mechanischen Eigen- 

schaften wie Fließkriterien bzw. Fließhypothesen 

3.1 Partikelmechanik und Partikelhaftkräfte in Schüttgütern 

3.1.1 Molekulare Wechselwirkungen und Partikelhaftkräfte 

• Wechselwirkungspotentiale zw. Atomen und Molekülen, Folie F 3.4 

• Wechselwirkungspotentiale zw. Atomen und Molekülen, Folie F 3.5 

• Wechselwirkungspotentiale eines polaren Molekülpaares, Folie F 3.6 

• Geschwindigkeitsabhängiges Fließen monodisperser kugelförmiger Mo- 

leküle: Folie F 3.7 

• Wechselwirkungsenergie zwischen Atomen, Ionen und Molekülen im 

Vakuum: Folie F 3.8 

• Wechselwirkungskräfte und –potentiale zwischen glatten, steifen Mo- 

dellkörpern: Folie F 3.9 

3.1.2 Übersicht über wesentliche Partikelhaftkräfte in Schüttgütern 

• Partikelhaftung und Mikroprozesse der Partikelbindung zwischen unver- 

festigten Partikelkontakten: siehe F 3.10 

• Van-der-Waals-Haftkräfte zwischen steifen Partikeln mit weichen 

Kontakten: siehe F 3.11 

• Flüssigkeitsbrücken zwischen steifen Partikeln: siehe F 3.12 

• Festkörperbrücken zwischen steifen Partikeln: siehe F 3.13 

• Vergleich der Haftkräfte zwischen steifen Partikeln: siehe F 3.14 

1) Van-der-Waals-Kräfte 

• verursacht durch elektrische Dipolmomente von Atomen und Molekülen, 

siehe auch MVT_e_6.doc - Adhäsionsarbeit ff. 

• geringe Richtweite, nur im unmittelbaren Kontaktbereich wirksam 

• bei sehr trockenen Pulvern wirksam, werden durch Adsorptionsschichten 

beeinflußt, plastischer Repulsionskoeffizient κp: 

pVdW 

CH 

κ p = = 

3 

p 6 ⋅ π ⋅ a ⋅ p 

( 3.3) 

f 

0 

f 

CH = 3...45⋅10 -20 J HAMAKER-Konstante 



14

a ≈ a0 = 0,3...0,4 nm Gleichgewichtsabstand (≈ Durchmesser eines 

p ≈ 3⋅ 

σ 

Wassermoleküls) 

mikroplastischer Fließdruck (σf makroskopische Fließ- 

f 

f 

grenze bei Zugbeanspruchung) entspricht einer mikro- 

skopischen Materialhärte, pf ≈500 MPa für Kalkstein, pf 

≈ 20 GPa Tonerde (Korund) 

Isostatische (dreiachsige) Zugfestigkeit der unverfestigten Partikelkon- 

takte für Van-der-Waals-Kräfte 

1− 

ε 

F 

0 H0 

σ 0 = ⋅ 

mit ( 3.4) 

2 

ε0 

d 

( ) ⎥ CH, 

sfs⋅ 

d r ⎡ d / d ⎤ 

r 

F H0 

= ⋅ ⎢1 

+ 

( 3.5) 

2 

2 

12⋅ 

a 0 ⎣ 1+ 

d r /( 2 ⋅ a 0) 

⎦ 

dr ≈ 0,1 µm mittlere Rauhigkeitsabmessung 

d Partikelgröße 

ε0 

aus Gl.( 3.121) mit der Schüttdichte ρb,0 einer locke- 

ren Aufschüttung 

• Haftkraft = (1+κ)⋅Haftkraft im unverfestigten Zustand + κ⋅verfestigende 

(äußere) Normalkraft, siehe Gl.( 3.72) 

• elastisch-plastischer Kontaktverfestigungskoeffizient oder Haftkraftanstieg: 

κ = ϕ / tanϕ 

−1 

tan st i 

• einaxiale Druckfestigkeit σ c= a1⋅σ1 + σc, 

o 

• minimale Trichteröffnungsweite, siehe auch Schüttec_4.doc - bmin: 

( m + 1) 

σc, 

osin2( 

ϕW 

+ Θ) 

bmin 

= 

ρ ⋅g 

( 1− 

a ⋅ff 

) 

b 

2) Flüssigkeitsbrückenbindungen 

1 

• Feuchtigkeitsverteilung und Wasserbindung in Partikelpackungen, siehe 

Folie F 3.15 

• Adsorptionsschichtbereich, 

� Feuchtigkeitsbindung im Adsorptionsschichtbereich, s. Folie F 3.16 

� Dreiachsige Zugfestigkeit unverfestigter Partikelkontakte 

1− 

ε σ ⎛ 

Z, 

A ⋅ π⋅ 

a 0 

⋅ ⎜ 

XW 

σ0 

= 

ε 

⎜ 

0 d ⎝ XW 

, m 

a ⎞ 

− ⎟ 

2a 

⎟ 

0 ⎠ 

( 3.6) 

d Partikelgröße 

X = m / m Wassergehalt bezogen auf trockenes Gut, für Pulver 

W 

W 

s 

ist Xw ≈ 0,1 ... 0,4 % sehr gering 

σZ,A ≈ 10 MPa Zugfestigkeit einander "durchdringender" Wasseradsorptionsschichten 



15

M W ⋅ AS, 

m 

X W, 

m = 

A W ⋅ N A 

16 

Wassergehalt für ideale Monoschichtbelegung 

der Oberflächen der Partikeln 

NA=6,024 . 10 23 mol -1 AVOGADRO-Zahl 

AW=0,126 nm 2 Platzbedarf eines Wassermoleküls 

Mw= 18 kg/kmol Molmasse des Wassers 

AS,m 

massebezogene Oberfläche des Schüttgutes 

� Einaxiale Druckfestigkeit direkt abgeschätzt: 

0, 

75 

8, 

88⋅ 

( 1− 

ε) 

⋅σ 

lg ⋅sin 

ϕi 

⎛ ρ ⎞ s 

σ c = 

X 

0, 

75 

W 

d ( 1 sin i ) ⎜ ⋅ ⎟ 

ε ⋅ ⋅ − ϕ ⎝ ρl 

⎠ 

( 3.7) 

σlg =72 . 10 -3 J/m 2 Grenzflächenspannung des adsorbierten Was- 

• 

sers 

ab etwa einer relativen Luftfeuchte ϕ = pD/pDS = 0,8 (Dampfdruck/Sattdampfdruck) 

tritt Kapillarkondensation an den Partikelkontakten ein. 

Das entspricht etwa Xw = 0.3 bis 0,8 % je nach spezifischer Oberfläche 

eines Pulvers, siehe Bild F 3.16; 

• Brückenbereich 

� voll ausgebildete Flüssigkeitsbrücken 

8, 

25⋅ 

( 1− 

ε)( 

2 − ε) 

⋅σ 

lg ⋅sin 

ϕi 

σ c = 

ε ε ⋅ d ⋅ 1− 

sin ϕ 

ρs 

XW 

ρ 

( 3.8) 

( ) 

i 

� gewöhnlich für Sättigungsgrad (Flüssigkeitshohlraumanteil) 

ρs 

( 1− 

ε) 

⋅ X W 

S = < 0, 

3 

( 3.9) 

ρ ⋅ε 

l 

� Berücksichtigung innerer Feuchte kapillarporöser Partikel 

� innere Feuchte in den Kapillaren und Mikroporen der Partikel 

� Kapillarkondensation beschreibbar mit der Kelvin-Gl. bei ϑ = 20° C 

4 

p ⎡ ⎤ ⎛ 

⎞ 

D M W ⋅ pK 

7, 

389 ⋅10 

= ϕ = exp⎢− 

⎥ ≈ exp ⎜ 

⎜− 

⋅ pK 

⎟ 

pS 

⎣ ρW 

⋅ R ⋅ T ⎦ ⎝ bar ⎠ 

( 3.10) 

M W = 18kg 

kmol Molmasse des Wassers 

ρ W 

3 

= 10 kg 

3 

m 

Dichte des Kondensates (Wasser) 

J 

R = 8, 

3145 

mol ⋅ K 

allg. Gaskonstante 

3) Festkörperbrücken 

Festkörperbrücken sind außerordentlich problematisch für die Handhabung 

der Schüttgüter ⇒ praktische Beispiele der Bildung der Festkörperbrücken: 

• KCl 99 Kristallisationsbrücken d = 100 - 600 µm, siehe F 3.17 

• Sinterbrücken für PVC-U, siehe F 3.18 

• Sinter- u. Kristallisationsbrücken einer Naßasche (Schlacke), s. F 3.19 

• Spannungsübertragung in den Partikelkontakten, F 3.20 



l

a) Kristallisationsbrücken 

• durch Austrocknung von Flüssigkeitsbrücken bestehend aus gesättigten 

Lösungen löslicher Inhaltsstoffe des Schüttgutmaterials 

• für leichtlösliche Schüttgüter als Zeitverfestigungen, F 3.21 

⎡ t ⎤ 

σ ct = σDs 

⋅ ( 1− 

ε) 

⋅ YS 

⋅ ( X W0 

− X WE ) ⎢1 

− exp( − ) ⎥ ( 3.11) 

⎣ t 63 ⎦ 

σDs Druckfestigkeit des kristallisierenden Feststoffes (= 30 

MPa für Sylvinit) 

YS =msl/mw Sättigungslöslichkeit (= 0,341 bei 20°C für Sylvinit) 

msl Masse gelöster Stoff 

mw Masse Wasser 

XW0 Anfangsfeuchte 

XWE End- bzw. Gleichgewichtsfeuchte 

t Lagerzeit 

t63 Stofftransportwiderstand des Wassers im Schüttgut 

• wenn t = t63 sind 63 % von der Endfestigkeit erreicht t63 = f (spez. Oberfläche, 

Porosität, Temperatur, Diffusionsweg ...) 

⇒ berechenbar für diffusionsgesteuerten Stofftransport, F 3.21 

b) Brücken durch chemische Reaktionen 

• Einbau von Wasser in das Kristallgitter, = Hydration bei hydraulischen 

Bindemitteln (Zement, Gips, Aschen), Bild F 3.22 

• Wassergehalte meist im Adsorptionsschichtbereich XWA ≈ 0,1 ... 0,4 % 

falls nicht aus Umweltgründen Wasser zugegeben (Staubbindung) 

Ms 

⋅ X WA k W ⋅ t 

σ ct = σDs 

⋅( 

1− 

ε) 

⋅ ⋅ 

M ⋅ϑ 

k ⋅ t + 1 

( 3.12) 

W 

W 

W 

σDs ≈ 35 MPa Druckfestigkeit eines Betonmörtels B 35 aus Portlandzement 

(PZ 1/35) 

Mw= 18 kg/kmol Molmasse des Wassers 

Ms ≈ 5400 kg/kmol Molmasse des hydratisierten Feststoffes 

νw ≈ 64 stöchiometrischer Faktor einer Beispielreaktion des 

Stoffes + ϑ ⋅ H O ⇔ hs zu hydratisiertem Gut 

s W 2 

kw ≈ 97 d -1 Geschwindigkeitskonstante der Reaktion (hier z.B. Zement) 

⎛ EA 

⎞ 

k W = k W∞ 

( Am 

) ⋅exp⎜− 

⎟ 

⎝ R ⋅T 

⎠ 

( 3.13) 

EA Aktivierungsenergie 

kw∞ Konstante für T → ∞ 

⇒ alles gültig σct ↔ σDs für spröde Materialien 



17

c) Brücken durch Sintervorgänge 

• für weiche, plastische, bzw. viskos bis viskoplastisch-fließende Materia- 

lien z. B. Plastpulver, Futter- u. Nahrungsmittel, ab einer Temperatur 

von etwa 

T = (0,75 ... 0,9)⋅Tm ( 3.14) 

der Schmelztemperatur möglich, F 3.23 

• Der innerer Reibungswinkel der Zeitverfestigung ϕit ist physikalisch 

sinnvoll über eine Beziehung mit dem stationären Reibungswinkel ϕst 

verknüpft, siehe auch Gl.( 3.104): 

( 1+ 

κ + κ ) ⋅ tan ϕ = const. 

≠ f ( t) 

tan st = 

t 

it 

ϕ ( 3.15) 

Damit folgt für den Anstiegswinkel des linearen Zeitfließortes, Gl.(3.81) 

im Abschnitt 3.2.4: 

tan ϕi 

tan ϕ it = 

2 ⋅σ 

Zs ⋅ tan ϕi 

⋅ t 

1+ 

5⋅ 

η T ⋅ tan ϕ 

( 3.16) 

s 

( ) st 

σ 10MPa... 

Zugfestigkeit des Feststoffes 

Zs = 

10 Pa s 

13 

η > ⋅ 

Feststoffviskosität 

s 

mit der Temperaturabhängigkeit der Festoffviskosität: 

( ) ⎟⎟ 

⎛ E γ� 

⎞ 

η = η ⋅ ⎜ 

s s, 

min exp 

⎝ R T − Tr 

⎠ 

E sog. "Aktivierungsenergie" 

γ� 

200 K < Tr < 400 K Temperaturparameter 



( 3.17) 

R = 8315 J/(kmol K) allgemeine Gaskonstante 

1− 

ε F 1 

t 

0 H0, 

t − ε π ⋅ σ 0 Zs ⋅ σsg 

⋅ 

σ 0t 

= ⋅ = ⋅ 

2 

ε d ε 5 ⋅ η ⋅ d 

( 3.18) 

σsg 

0 

0 

s 

spezifisch freie Grenzflächenenergie (Grenzflächenspannung 

fest-gasförmig) ≈ 0,1 ... 1 J/m² 

3.1.3 Mechanik eines weichen adhäsiven Partikelkontaktes 

• Partikelkontaktdeformation in Normalrichtung ohne Haftung, s. F 3.24 

• Mikromechanik der Partikelkontaktkräfte, Drehmomente und ihre je- 

weiligen Kraft - Weg und Drehmoment - Winkel Beziehungen, s. F 3.25 

→ Nächste 25 Folien: Zusätzliche Bilder der Grundlagen der Kontaktmechanik 

adhäsiver feiner (d < 100 µm), ultrafeiner (d < 10 µm) bis 

nanaoskaliger Partikel (d < 0,1 µm) 

3.1.3.1 Normalkraft-Weg-Beziehungen 

18

• Übersicht über die Stoffmodelle der Partikelkontaktdeformation (Stau- 

chung) von Kugeln in Normalrichtung ohne und mit Haftung, 



siehe Folie F 3.26 

• Übersicht über die Stoffmodelle der Partikelkontaktdeformation (Stau- 

chung) von Kugeln in Normalrichtung ohne und mit Haftung ff, 


• Übersicht über Stoffmodelle der Kontaktreibung glatter Kugeln in Tan- 

gentialrichtung ohne und mit Haftung, siehe Folie F 3.28 

• Charakteristische Partikelkontaktdeformation von Titandioxid 

Sauterdurchmesser dST = 200 nm, Feuchte XW = 0,4 %, siehe Folie F 3.29 

• Kontaktdeformationsarten glatter Kugeln und deren räumliche Span- 

nungsverteilungen, s. F 3.30 

• Normalkraft-Weg-Modelle der charakteristischen 

Partikelkontaktdeformationen, s. F 3.31 

• Viskoelastische - viskoplastische Partikelkontaktdeformation für Titandi- 

oxid d50 = 610 nm, Feuchte XW = 0.4 %, Einwirkzeit t = 24 h, s. F 3.32 

• Charakteristische Partikelkontaktdeformation für Titandioxid d50 = 610 

nm, Feuchte XW = 0.4 %, s. F 3.33 

• Plastische Kontaktdeformation und Haftung/Rückprall bei zentraler 

Stoßbeanspruchung, s. F 3.34 

• Partikelkontaktkräfte und Haftkraftverstärkung für TiO2-Pulver, s. F 3.35 

• Haftkraft - Partikelgröße - Diagramm für TiO2 – Pulver, Parameter: 

Normalkraft, s. F 3.36 

3.1.3.2 Tangentialkraft-Weg-Beziehungen 

• Charakteristische Partikelkontaktverschiebung zweier TiO2-Partikel, Partikelgröße 

dST = 200 nm, Feuchte XW = 0,4 %, s. F 3.37 

• Kontaktdeformationsarten glatter Kugeln und deren räumliche Spannungsverteilungen, 

s. F 3.38 

3.1.3.3 Rollmoment-Rollwinkel-Beziehungen 

• Charakteristischer Rollwiderstand zweier TiO2-Partikel, Partikelgröße 


3.1.3.4 Torsionsmoment-Drehwinkel-Beziehungen 

• Charakteristische Partikelkontakttorsion zweier TiO2 – Partikel, Partikelgröße 


3.1.3.5 Vergleich der charakt. Haft- und Reibungsgrenzen 

• Vergleich der lastabhängigen Haftgrenze FH und der elastisch-plastischen 

Reibungsgrenzen der Tangentialkraft FT,CH, des Rollmomentes MR,CH u. 

19

des Torsionsmomentes Mto,CH eines charakteristischen TiO2 - Partikel- 

kontaktes, Partikelgröße dST = 200 nn, Feuchte XW = 0,4 %, s. F 3.41 

3.1.3.6 Hysterese-, Ablöse- & Reibungsarbeit des lastabhängigen Partikel- 

kontaktes 

• Elastische Hysteresearbeit, Ablöse- und Reibungsarbeit für die lastab- 

hängige Partikelhaftung, s. F 3.42 

• Vergleich der lastabhängigen maximalen Arbeit der elastischen Hysterese 

der Deformation in Normalrichtung Wm,diss, der tangentialen 

Mikroschlupfes Wm,T,max, der Rollreibung Wm,R,max und des Torsionsmo- 

mentes Wm,to,max eines TiO2 - Partikelkontaktes, Partikelgröße dST = 200 

nm, Feuchte XW = 0,4 %, s. F 3.43 

• Vergleich der lastabhängigen maximalen Ablöse- und Reibungsarbeit der 

Kompression und Ablösung in Normalrichtung Wm,N,A, der Gleitens 

Wm,T,C, der Rollreibung Wm,R,C und des Torsionsmomentes Wm,to,C eines 

TiO2 - Partikelkontaktes, dST = 200 nm, Feuchte XW = 0,4 %, s. F 3.44 

• Vergleich der chakteristischen Aktivierungsenergie (max. Kompressions- 

und Reibungsarbeit) für Kompression und Ablösung, Gleiten, Rollen und 

Torsion eines TiO2 - Partikelkontaktes, dST = 200 nm, XW = 0,4 %, 

3.1.3.7 Weicher adhäsiver Partikelkontakt in Wasser 

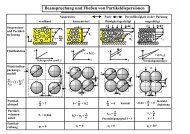
• Beanspruchung und Fließen von Partikeldispersionen, s. F 3.46 

• Partikelwechselwirkungen in Luft und Wasser, s. F 3.47 

• Partikelwechselwirkungen in Luft und Wasser ff, s. F 3.48 

3.1.3.8 Festkörperbrückenbindungen im Partikelkontakt 

• Bindungskräfte einer Festkörperbrücke, s. F 3.49 

• Bindungskräfte einer Festkörperbrücke ff, s. F 3.50 

→ Details siehe auch: 



s. F 3.45 

Tomas, J., Adhesion of ultrafine particles - a micromechanical approach, 

Chemical Engineering Science 62 (2007), 1997-2010, doi: 

10.1016/j.ces.2006.12.055 

..\..\..\Forschung\FLIESSEN\Adhäsion\CES\Tomas_CES_2006_revised.doc 

..\..\..\Forschung\FLIESSEN\Adhäsion\CES\Offprint_Tomas_CES_7149.pdf 

3.1.4 Messung der Kontaktkräfte 

• Messung der Haftkraft zwischen Partikel und Oberfläche, s. F 3.51 

20

• Messung der Haftkraft - Weg - Funktion mittels Rasterkraftmikroskop 

(AFM) nach BUTT, s. F 3.52 

• Messung Intermolekularer Kräfte und Oberflächenkräfte, s. F 3.53 

3.1.5 Modelle bimodaler kubischer Partikelpackungen 

• Packungszustand monodisperser Kugeln, s. F 3.54 

• Einbettung des Grobkorns im Feinkorn kubischer Packungen bimodaler 

Kugeln, s. F 3.55 

3.1.6 Mikro-Makro-Übergang in einer bewegten Partikelpackung 

• Mikro-Makro-Übergang, Kraft- und Spannungsübertragung in einer gescherten 

Partikelpackung nach MOLERUS und TOMAS, s. F 3.56 

• Mikro-Makro-Übergang, Kraft- und Spannungsübertragung in einer gescherten 

Partikelpackung nach TOMAS, Forts., s. F 3.57 

3.1.7 Einführung in die Diskrete-Elemente-Methode (DEM) 

Weitere 10 Zusatzbilder zur DEM: 

• Partikelkontaktdynamik und Simulation der Dynamik einer Partikelpackung 

mittels Diskrete-Elemente-Methode (DEM), s. F 3.58 

• Der Partikelkontakt als mechanisches Schwingelement, 

Freie, ungedämpfte Schwingung, s. F 3.59 

• Der Partikelkontakt als mechanisches Schwingelement, Forts., 

Freie, gedämpfte Schwingung s. F 3.60 


Erzwungene, gedämpfte Schwingung s. F 3.61 


Verschaltung mechanischer Federelemente s. F 3.62 

• Diskrete-Elemente Methode - Bewegungsgleichungen, s. F 3.63 

• Diskrete-Elemente Methode - Kraft-Weg-Gesetze des Partikelkontaktes, 

s. F 3.64 

• Diskrete-Elemente Methode - Numerischer Algorithmus, s. F 3.65 

• Diskrete-Elemente Methode - Numerische Lösungsmethode, s. F 3.66 

• Diskrete-Elemente Methode - Eingabedaten (mechanische Stoffwerte), 

Prozess- und Zielfunktionen sowie Ausgabedaten, s. F 3.67 



21

3.2 Kontinuumsmechanische Grundlagen des Fließverhaltens vorver- 

dichteter Partikelpackungen 

3.2.1 Zweiachsiger Spannungszustand 

• „Vorverdichtet“ bedeutet hier allg.: die mechanische Eigenschaften der 

Partikelpackungen hängen unmittelbar von der Beanspruchungsvorgeschichte, 

d.h. von Betrag und Richtung der eingeprägten Kräfte und der 

Beanspruchungsgeschwindigkeiten ab 

• Kräftegleichgewicht an einem Schüttgut-Volumenelement, s. F 3.68 

• Vorzeichendefinition 

• Druckspannungen positiv, Zugspannungen negativ, 

• Verdichtung positiv, Ausdehnung = negative Volumenänderung, 

• positives Auftragen von Winkeln im mathematisch positiven 

Drehsinn, d.h. entgegen dem Uhrzeigersinn, 

• Eine Schubspannung τ xy bedeutet: 

- 1. Index: x - Richtung der Flächennormalen, 

- 2. Index: y - Kraftrichtung, 

- treten paarweise auf, betragsmäßig gleich: xy = τyx 



τ , xy yx 

22 

τ = −τ 

, 

- und sind → momentenfrei! 

• positive Richtung einer Schubspannung, 

- wenn diese mit der Richtung der im mathematisch positiven Sinne 

um 90° gedrehten, im Volumenelement nach innen zeigenden 

Normalen der Schnittfläche übereinstimmt, oder 

- wenn beide Richtungen, sowohl die Flächennormalenrichtung als 

auch die Spannungsrichtung positiv sind, 

- wenn beide Richtungen, sowohl die Flächennormalenrichtung als 

auch die Spannungsrichtung negativ sind, 

• Im allgemeinen dreiachsiger Spannungszustand eines Volumenelements: 

dV = dx ⋅ dy ⋅ dz 

( 3.19) 

y 

z 

x 

dx 

dz 

dy 

Bild 3.4: Abmessungen eines inkrementellen 

Volumenelements 

• aber nur zweiachsiger, d.h. ebener Spannungszustand betrachtet: 

• lineares Fortschreiten der Spannungen nach einer Taylor-Reihe, 

• 

2 

df 

( ) ( ) 

( x) 

1 d f ( x) 

2 

f x + ∆x, 

y = f x + ⋅ ∆x 

+ ⋅ ∆x 

+ ... 

2 

dx 2! 

dx 

( 3.20) 

• z.B. in x-Richtung mit Abbruch nach der ersten Ableitung:

σx 

dy 

dz 

δσ 

x 

σ σ 

x x x δx 

dx 

+ = + ∆σ 

Bild 3.5: Horizontalspannungen am Volumenelement 

→ Kräftegleichgewicht ∑ F →= 0 

∂σx 

0= 

σx⋅dy⋅dz−σx⋅dy⋅dz− 

dxdydz 

∂x 

und komplett, siehe F 3.68 

∂τyx 

0= 

σx⋅dy⋅dz+ 

τyx⋅dx⋅dz−( 

τyx+ 

dy 

∂y 

) dxdz 

−σ 



x 

∂σ 

dydz− 

∂x 

x 

dxdydz 

∂τyx 

∂σx 

0 = + 

( 3.21) 

∂y 

∂x 

∂τxy 

∑ F↓= 

0= 

σy 

⋅dxdz+ 

τxy⋅dydz−( 

τxy+ 

dx) 

dydz 

∂x 

∂σy 

− ( σy+ 

dy) 

dxdz+ 

ρb⋅g⋅dy⋅dz⋅dx 

∂y 

∂σy 

∂τxy 

ρ b⋅g 

= + 

( 3.22) 

∂y 

∂x 

→ 2 Gleichungen aber 3 Unbekannte, d.h. gesucht wird eine weitere Gl., 

d.h. Fließkriterium bzw. "Stoffgesetz", siehe Gl.( 3.61) 

� zusätzlich: rotationssymmetrischer Spannungszustand, Draufsicht: 

ψ 

y 

σψ 

+ ∆σ 

σx 

dψ 

xdψ 

x 

dx 

σ 

x x 

dψ σψ 

x 

x 

σψ dψ 

Bild 3.6: Kreissegment eines axialsymmetrischen Schüttgutelements 

σ ⋅xdψ⋅dy+ 

σ dxdψdy−( 

σ 

x 

ψ 

x 

+ ∆σ 

x 

)( x+ 

dx) 

dψdy= 

0 

∂σx 

∂σx 

≈ 0 sehr klein 

σx 

⋅x+ 

σψ 

dx−σ 

x x−σ 

xdx− 

dx⋅x− 

dx⋅ 

dx= 

0 

∂x 

∂x 

σx 

−σψ 

∂σx 

0 = + 

x ∂x 

23 

( 3.23) 

Berücksichtigung in der allg. Gleichung siehe F 3.68 mittels Faktor m = 1 

σx 

−σψ 

für den Term: m ⋅ , siehe Trichterdimensionierung Schüttec_4.doc - 

x 

Trichterformfaktor_m im Abschnitt 4. 

Bogenlänge: 

π ⋅ d = 360° 

π ⋅ r = 180° 

dψ ⋅ r = dψ 

⋅ x 

∑ 

F →= 0

→ Mechanische Grundmodelle für elastisches, plastisches und 

viskoses Stoffverhalten, siehe F 3.69 

Zweiachsige Spannungszustände am Mohrschen Spannungskreis 

• Suche eines Fließkriteriums in der Weise, das die Unabhängigkeit von 

einem willkürlich gewählten Koordinatensystem garantiert ist 

• d.h. für ein Schüttgutprisma der Länge dz, siehe F 3.70 

Bild 3.7: zweiachsigerSpannungszustand 

am homogenenSchüttgutprisma 

dy 

τxy 

σx 

α 

- Druckspannungen und damit Kompression sind positiv definiert, 

- Schubspannungsrichtung ist positiv, wenn sowohl der 

Flächennormalenvektor als auch die Achsenrichtung positiv (vom Nullpunkt 

wegzeigen) oder beide negativ sind. 

- α-Winkel ist positiv, wenn er entgegen dem Uhrzeigersinn aufgetragen 

wird, 

Kräftegleichgewichte 

• in σα-Richtung: ∑ F σ = 0 α 

σα ⋅ds 

⋅dz 

− σx 

cos α ⋅dy 

⋅dz 

− σy 

sin αdxdz 

− τxy 

sin αdydz 

− τyx 

cos α dxdz = 0 

dy = ds ⋅ cos α 

außerdem sind: 

und τ xy = τyx 

dx = ds ⋅ sin α 

2 

2 

σα⋅ds−σx ⋅dscos 

α−σysin 

αds−τxysincosαds− 

τxy 

cosα⋅sinαds= 

0 mit 

2sinα⋅ 

cosα 

= sin2α 

2 1 

cos α = ( 1+ 

cos2α) 

2 

2 

2 

σα = σx 

cos α+ 

σysin 

α+ 

2τxysinαcosα 

σx 

σx 

2 

= + cos2α+ 

σy 

( 1−cos 

α) 

+ τxysin2α 

2 2 

σ σ 

σ σ 

x x 

y y 

= + cos2α+ 

σy 

− − cos 2α+ 

τxysin2α 

2 2 

2 2 

σx 

+ σ y σx 

−σ 

y 

σα = + cos2α+ 

τxysin2α 

( 3.24) 

2 2 


σα 

σy 

τα 

ds 

dx 

τyx 


σxcosα 

dz 

α 

σy 

σx 

α 

24 

σysinα 

α

∑ τ α 

Kräftegleichgewicht in τα-Richtung: F = 0 

0 = τ 

0= 

τ 

α 

α 

⋅ ds ⋅ dz + σ 

dxdz cos α −τ 

⋅ ds + σ dssin 

α cos α − σ dssin 

α cos α − τ 

x 

dydzsin 

α − σ 

x 

2 

2 

− cos α + sin α = − cos 2α 

σ σ 

x 

y 

τα = − sin 2α 

+ sin 2α 

+ τxy 

cos 2α 

2 2 

σx 

− σy 

τα = − sin 2α 

+ τxy 

cos 2α 

2 

Hauptspannungen: 

y 

y 


xy 


cos αdydz 

+ τ 

xy 

cos 

2 

yx 

αds 

+ τ 

xy 

sin αdxdz 

sin 

2 

αds 

25 

( 3.25) 

• gesucht der Winkel, bei dem σ α maximal bzw. minimal wird, d.h. aus 

Gl. ( 3.24) 

dσ 

σ 

= 0 = −2 

dα 

− σ 

α x y 

sin 2α 

+ 2τxy 

cos 2α 

= 2τα 

2 

( 3.24) 

gemäß Gl. ( 3.25) verschwindet somit die Schubspannung τ α = 0 

Der Winkel αo ist dann: 

2τxy 

tan 2α 

o = 

σ −σ 

π 

= tan 2( 

αo 

+ ) 

2 

( 3.26) 

x 

y 

wegen der Periodizität der Tangensfunktion in π 

• Es gibt 2 Flächen, die aufeinander senkrecht stehen, bei denen τα = 0 

verschwindet. Die Normalspannungen auf diese Flächen werden größ- 

te und kleinste Hauptspannung genannt. D.h. 

σx 

+ σy 

σx 

σ1 

= + 

2 

− σy 

cos 2αo 

+ τxy 

sin 2αo 

2 

σ2 

σx 

= 

+ σy 

σx 

− 

2 

− σy 

cos 2αo 

− τxy 

sin 2αo 

2 

⎛ σx 

⎜ 

⎜σ 

α − 

⎝ 

2 

+ σy 

⎞ ⎛ σx 

− σy 

⎞ 

= cos 2 xy sin 2 

2 ⎟ 

⎜ 

α + τ α 

2 

⎟ 

⎠ ⎝ 

⎠ 

⎛ σ 

⎜ 

⎝ 

x 

− σ 

2 

⎛ σ 

+ ⎜ 

⎜− 

⎝ 

x 

y 

τ 

2 

α 

− σ 

2 

⎛ σ 

= ⎜ 

⎜− 

⎝ 

⎞ 

cos 2α 

⎟ 

⎠ 

y 

2 

x 

⎞ 

sin 2α 

⎟ 

⎠ 

2 

2 

wobei 1 = sin α + cos α gilt. 

⎛ σx 

+ σy 

⎞ 2 

⎜σ 

α − ⎟ + τα 

= 

⎝ 2 ⎠ 

2 

− σ 

2 

y 

⎛ σx 

− σ 

+ 2 ⎜ 

⎝ 2 

2 

⎛ σx 

− σ 

⎜ 

⎝ 2 

sin 2α 

+ τ 

y 

⎛ σx 

− σ 

− 2 ⎜ 

⎝ 2 

y 

2 

⎞ 

⎟ 

⎠ 

+ τ 

2 

xy 

xy 

2 

⎞ 

cos 2α 

⎟ 

⎠ 

⎞ 

⎟ cos 2α 

⋅ τ 

⎠ 

y 

cos 

xy 

⎞ 

⎟ 

⎟sin 

2ατ 

⎠ 

2 

2α 

2 

sin 2α 

+ τ 

xy 

2 

xy 

cos 2α 

+ τ 

sin 

2 

xy 

2 

cos 

2α 

2 

2α 

( 3.27) 

Dies ist nun die allgemeine Gleichung des Mohrkreises. Für das Ver- 

schwinden der Schubspannung τxy = 0 gilt ebenfalls

* π 

α = α0 

± 

( 3.28) 

4 

und somit auch die folgenden Gleichungen, F 3.70 

2 

⎛ σ1 

+ σ2 

⎞ 2 σ1 

− σ2 

⎜σ 

− ⎟ + τ = 

oder ( 3.29) 

⎝ 2 ⎠ 2 

2 2 2 

( − σM 

) + τ = σR 

σ mit der ( 3.30) 

Radiusspannung 

und der Mittelpunktsspannung 

σ1 

+ σ2 

σ1−σ 

2 

σ = + cos2α 

2 2 

σ1 

−σ2 

τ = − sin2α 

2 

σ1−σ 

2 

τ max = − für sin2α= 

1 

2 

1 π 

d. 

h. 

α = arcsin( 

1) 

⋅ = 

2 4 

σ1 

− σ2 

σ R = 

2 

( 3.31) 

σ1 

+ σ2 

σ M = 

2 

( 3.32) 

Bild 3.8: zweiachsige Hauptspannungen am Schüttgutprisma 

Die Richtungen der Hauptspannungen lassen sich durch eine Dreiecks- 

beziehung im Kreis (Satz des Thales) ermitteln, F 3.71. 

Übung 

bei gegebenen Hauptspannungen σ1, σ2 und Gleitwinkel α 

gesucht: σx = ?, σy = ?, τxy = ? 

Bild 3.9: Grafische Darstellungen 

der Spannungen im zweiachsigen 

Spannungszustand mit einem sog. 

MOHR-Kreis 

Bild 3.10: zweiachsiger Spannungszustand 

Der Winkel α wird entgegen dem Uhrzeigersinn abgetragen 



τ 

σy 

σ1 

τyx σR 

σM 

σx 

2α 

τxy 

α 

σx 

σ 

τ 

σ2 

σ2 - Richtung 

τxy 

τ = 0 

α 

σy 

σ1 

σ 

σ1 

τyx 

26

⇒ Berücksichtigung des Vorzeichens (-) in der Gl.( 3.35) durch Auftragen 

im Uhrzeigersinn 

σ1 

+ σ2 

σ1 

− σ2 

σx = + ⋅ cos 2α 

2 2 

( 3.33) 

σ1 

+ σ2 

σ1 

− σ2 

σy = − ⋅ cos 2α 

2 2 

( 3.34) 

σ1 

− σ2 

τxy = − ⋅ sin 2α 

2 

( 3.35) 

oder auch mit den Mittelpunkts- und Radiusspannungen: 

σx = σM 

+ σR 

⋅ cos 2α 

( 3.36) 

σy = σM 

− σR 

⋅ cos 2α 

( 3.37) 

τxy = −σR 

⋅ sin 2α 

( 3.38) 

→ Richtungsabhängige (anisotrope) aktive und passive Rankinesche 

Grenzspannungszustände, siehe F 3.72 

3.2.2 Kontinuumsmechanische Fließkriterien (Bruchhypothesen) 

• Formulierung sog. Bruchhypothesen für mehrachsige Spannungszustände, 

d.h. Fließkriterien, die dann das Materialverhalten charakterisieren 

sollen (Rückführung auf einachsige Beanspruchungsstände) 

• Übersicht über die Entwicklung der Fließkriterien und Bruchhypothesen, 


• Vergleichsspannungshypothesen bei mehrachsigen Spannungszuständen 

• in Bauteilen meist mehrachsige Spannungszustände 

(1) Hauptspannungshypothese 

• maximale Hauptnormalspannung für den Bruch verantwortlich 

σ V = σ1 

wenn σ 1 > σ2 

> σ3 

• für duktiles (dehnbares, zähes) Material σv zu klein, d.h. unsicher, angenommen 

(2) Hauptdehnungshypothese 

• Bruch tritt bei der größten Dehnung ε = ∆l/l0 

/ F = σ 

ein, N o A 

l − l0 

ε y = ε = > 0 ( 3.39) 

l 

0 

Verdichtung ist positiv (+) vereinbart und 

d0 d 

Dehnung ist negativ (-) vereinbart 

d0 

− d ∆d 

Querdehnung: ε x = εq 

= = < 0 

d d 

Bild 3.11: Deformationen eines 

zylindrischen Volumenelementes 

( 3.40) 

0 



0 

y 

∆l 

x 

σ 

27 

l 0

Es ist = −ν 

⋅ε 

ε q mit ν - Querdehnungszahl (bzw. Querkontraktions- 

zahl = 0,3 für Metalle), siehe Hookesche Gesetz: 

1 

ε = ⋅ σ bzw. σ = E ⋅ ε 

E 

( 3.41) 

E = Elastizitätsmodul (Steifigkeit oder Deformationswiderstand) 

E = 210 kN/mm² (GPa) für Stahl und E = 70 kN/mm² für Aluminium 

Verschiebung für γ

* 1 2 2 

1 2 

WF = ( σx 

+ σy 

−2σ 

xσ 

y ) + τxy 

( 3.49) 

2E 

2G 

→ Die Formänderung bei einem isostatischen Druck- oder Spannungszu- 

stand führt zu keinem Bruch! D.h. für eine mittlere Spannung 

1 

σ m = ( σx 

+ σy 

+ σz 

) 

3 

( 3.50) 

→ und einer gesamten Volumenänderung 

dV 

e= = ε x + ε y+ 

ε z 

V 

( 3.51) 

0 

→ entsteht eine Volumenänderungsarbeit 

* 1 1−2ν 

2 

Wv = σm⋅ 

e = ( σx 

+ σy 

+ σz 

) 

2 6E 

( 3.52) 

W 

die „wirksame“ Gestaltänderungsarbeit ist folglich 

* 

G 

2 

* * 1 ⎡ 

= W 

⎛ ⎞ 

F −WV 

= ⎢⎜σ 

− σ ⎟ + 

12G 

⎣⎝ 

x y ⎠ 

→ für den einachsigen Druck ist 

W 

* 

G( 

1) 

2 

+ 

( σ − σ ) 

2 2 2 2 ⎤ 

( σy 

−σz 

) + 6 ⋅ ( τxy 

+ τxz 

+ τyz 

) ⎥⎦ 



x 

z 

2 

( 3.53) 

2σV 

= ( 3.54) 

12G 

→ und bei gleicher Gestaltänderungsarbeit WG(1) * = WG* des allgemeinen 

σ 

V 

dreiachsigen Spannungszustandes folgt für die Vergleichsspannung 

= 

1 ⎡ 

⋅ 

2 

⎢ 

⎣ 

2 

2 

2 2 2 2 ⎤ 

( σx 

−σ 

y ) + ( σx 

−σz 

) + ( σy 

−σz 

) + 6 ⋅ ( τxy+ 

τxz 

+ τyz 

) ⎥⎦ 

(4) Hypothese von Huber-Mises-Hencky 

( 3.55) 

• Bruch tritt nach Erreichen der gleichen maximalen Gestaltänderungs- 

arbeit ein wie bei einem einachsigen Spannungszustand, siehe entspre- 

chend Hypothese (3) 

• Nutzung im Maschinen- und Anlagenbau! 

• Vergleichsnormalspannung σ V ≤ σzul. d.h. 

2 2 2 2 ⎤ 

( σ −σ 

) + σ + σ + 6τxy 

≤σ 

zul 

1 ⎡ 

σ V = σ1= 

⋅ x y x y 

2 

⎢ 

⎥ 

( 3.56) 

⎣ 

⎦ 

Für eine große Anzahl von Stoffen reicht diese kontinuumsmechanische 

Bruchhypothese nicht mehr aus, da das Versagen des Werkstoffes schon 

durch geringere Schubspannungen τzul < σzul verursacht wird. Der Zu- 

sammenhang einer Schubspannung als Funktion der Normalspannung τ = 

f(σ) (hier werden Druckspannungen positiv dargestellt) wird für ein gege- 

29

enes Material durch die Einhüllende aller MOHR-Kreise dargestellt, die 

den Bruchzustand charakterisieren: 

(5) Schubspannungshypothese von Tresca 

• Bruch durch maximale Schubspannung τmax, siehe Folie F 3.73 

• beispielsweise: Bruch schon nach halber Größe der Druck- bzw. Zug- 

festigkeit bei einaxialer Belastung 

• Bruch- oder Scherfläche um den sog. Gleitwinkel von α = π/4 = 45° 

zur Richtung der beiden Hauptspannungen geneigt, 

σy 

σc 

τ max= 

= 

2 2 

• Vergleichsspannung V 2 τmax 

⋅ = σ 

• Für die Vergleichsspannung gilt: 

V 

max 

2 2 

[ ( σx 

−σy 

) + 4τxy 

] ≤ zul 

σ = 2τ = 

σ ( 3.57) 

Bild 3.14: Scherbruch bei einachsiger Belastung 

• Beschreibung des plastischen Fließens von zähen oder duktilen Werkstoffen, 

z.B. Metallen 

→ ungeeignet für: 

• spröde Werkstoffe, da σZug

⇒ Spannungszustände, die durch MOHR-Kreise gekennzeichnet sind, 

die die Umhüllende schneiden, können nicht existieren, weil das 

Fließen schon bei niedrigeren Spannungen eingetreten wäre. Andererseits 

charakterisieren MOHR-Kreise innerhalb der Umhüllenden 

Spannungszustände, die noch kein Fließen, sondern nur elastische 

Deformation herbeiführen. 

• Aufgabenstellung in der Bodenmechanik ist gewöhnlich die Gewährleistung 

der Stabilität, d.h. man muß im elast. Beanspruchungsbereich 

bleiben, daher ist Kenntnis der "ungefähren" Lage der Fließgrenze 

ausreichend. 

• Durch einfache Geradengleichung beschreibbar: 

τ = ϕ ⋅ σ + τ = tanϕ 

⋅ ( σ + σ ) 

( 3.60) 

tan i c i 

Z 

oder auch: im obigen Bild 3.15 liest man die Dreiecksbeziehung ab: 

σ1 

− σ2 

σ R = = sin ϕi 

⋅ ( σM 

2 

+ σZ 

) mit σ M 

σ1 

+ σ2 

= 

2 

( 3.61) 

oder in σ1 - σ2 - Koordinaten 

1+ 

sinϕ 

2 ⋅ sinϕ 

i 

i 

σ 1 = ⋅ σ2 

+ ⋅ σZ 

( 3.62) 

1− 

sinϕi 

1− 

sinϕi 

Kennwerte, F 3.73: 

ϕi Reibungswinkel bzw. µi = tanϕi Reibungskoeffizient 

σZ Zugfestigkeit (dreiachsig!) 

τc Kohäsion, svw. Scherwiderstand bei einer äußeren Normalspannung 

σ = 0; beachte jedoch das Wirken einer zusätzlichen 

inneren Druckspannung -σZ aufgrund der Partikelhaftung! 

τ c = tanϕi ⋅ σZ 

( 3.63) 

→ nicht geeignet: für fließende Schüttgüter bei geringen Spannungen σ 

< 100 kPa 

(7) Fließkriterium nach Jenike 

• Spannungen fließender kohäsiver Schüttgüter oft unter 100 kPa, 


• "modifizierter" Coulomb-Körper mit zumindest 3 Erweiterungen 

1. Unterscheidung in stationäres (zeitinvariantes) und beginnendes 

Fließen notwendig! 

⇒ stationäres kohäsionslosen Fließens von Schüttgütern, d.h. 

effektiver Fließort F 3.76: 

σR 

σ1 

− σ2 

= = sin ϕe 

( 3.64) 

σ σ + σ 

ϕe 

M 

1 

2 

effektiver (oder wirksamer innerer) Reibungswinkel 



31

⇒ folgt notwendiger Weise aus der Aufgabenstellung in der 

Schüttgutmechanik das Fließen erzwingen zu müssen 

⇒ eine Grenzspannungsfunktion für stationäres Fließen 

2. Grenzspannungsfunktionen hängen von der Verdichtung, d.h. 

Schüttgutdichte bzw. Porosität ab 

3. Grenzspannungsfunktionen haben jeweils einen Endpunkt =ˆ Zustand 

des „kohäsionslosen“ stationären Fließens, svw. effektives 

stationäres Fließen ⇒ liefert den sog. effektiven Fließort 

und zusätzlich nach Schwedes: 

4. Grenzspannungsfunktionen haben im Bereich kleiner Druckspannungen 

einen gekrümmten Verlauf 

⇒ aber: Grenzspannungsfunktion von Gesteinen auch oftmals gekrümmt; 

Grenzspannungsfunktion = Ort an dem plastisches 

Fließen bzw. der Bruch eintritt = Fließort = yield locus 

⇒ bis hierher Aussagen der Kontinuumsmechanik! 

3.2.3 Partikelmechanisch begründete Fließkriterien 

(8) Fließkriterium nach Molerus 

⇒ hier so benannt nach MOLERUS (1978), siehe Folie F 3.73 

� Erstmalige Einführung partikelmechanischer Haftkraftmodelle 

zur physikalisch begründeten Erklärung bisher nur kontinuumsmechanisch 

zugänglicher Stoffgesetze. 

� Grenzspannungsfunktion ist von der Wirkung der Haftkräfte zwischen 

den Partikeln abhängig 

� Nur irreversible, rein plastische Partikelkontaktdeformation Apl 

betrachtet (- Vorzeichen = Haftung, + Repulsion): 

∑ F = 0 = −FH 

0 − pVdW 

⋅ A pl − FN 

+ pf 

⋅ A pl 

( 3.65) 

� Diese mittleren mikroskopischen Kontaktkräfte FT und FN und die 

resultierenden Spannungen im Kontinuum τ und σ lassen sich unter 

bestimmten Voraussetzungen analytisch ineinander umrechnen 

(1-ε Packungsdichte): 

1− 

ε FT 

, FN 

τ , σ = ⋅ 

( 3.66) 

2 

ε d 

Mit zumindest 4 Erweiterungen bei σ < 100 kPa, F 3.73: 

1. stationäres Fließen kohäsiver Schüttgüter ist "kohäsiv" 

⇒ "stationärer Fließort" als Coulomb-Gerade 

σ R, 

st = f ( σM, 

st ) 

( 3.67) 

τ = f σ . ( 3.68) 

( ) 



32

2. Lage der Grenzspannungsfunktionen wird von der Vorverfestigung 

und davon abhängiges Wirken der Haftkräfte in den 

Partikelkontakten beeinflußt 

⇒ Übergang von der Kontinuummechanik zur Partikelmechanik 

⇒ Haftkraftzuwachs als ein lineares "Verfestigungsgesetz" 

F = F + κ ⋅ F 

( 3.69) 

H 

H0 

p 

N 

FH0 Haftkraft in den unverfestigten Kontakten 

FN "äußere" eingeprägte Normalkraft in den Partikelkontakten 

3. Physikalischer Zusammenhang zwischen dem stationären ϕst und 

dem inneren ϕi Reibungswinkel: 

tan st 

p 

i 

ϕ = ( 1+ 

κ ) ⋅ tan ϕ = const. 

( 3.70) 

4. Schar von Grenzspannungsfunktionen läßt sich nur mit 3 physikalisch 

begründeten Fließkennwerten plus dem Einfluß eines charakteristischen 

mittleren Druckes beschreiben: 

(1) ϕi - innere Festkörperreibung (Gleitreibung) versagender Partikelkontakte 

(2) ϕst - stationäre Partikelreibung, Zunahme der Reibung infolge 

verfestigende äußere Kräfte, abgeleitet aus κp Gl.( 3.69) 

(3) σ0 - dreiachsige Zugfestigkeit des unverfestigten Schüttgutes, 

abgeleitet aus FH0 Gl.( 3.69) 

(4) σM,st Einfluß der mechanischen Beanspruchungsvorgeschichte, 

svw. mittlerer Vorverfestigungsdruck, im Schüttgutkontinuum; 

unmittelbarer Zusammenhang zur Schüttgutdichte ρb = 

f(σM,st) Gl.( 3.121). 

(9) Einführung eines neuen elastisch-plastischen und viskoplastischen 

Fließkriteriums nach Tomas (1987/99): 

NEU!: Wesentliche Erweiterung bisheriger partikel- und 

kontinuumsmechanischer Bruchhypothesen durch Einführung neuer, 

physikalisch begründeter Modelle der 

� Momentanfließorte, stationären Fließorte und Verfestigungsorte 

für elastisch-plastische Kontaktdeformationen und reibungsbehaftetem 

Kontaktgleiten mit lastabhängiger Haftkraft sowie der 

� Zeitfließorte mit viskoplastischer Kontaktdeformation (Anfang 

1987 siehe Diss. B 1991, CET 2003): 

� Rein elastische Abplattungen unter der Einwirkung äußerer Kräfte 

sind für die Haftkraftverstärkung verhältnismäßig bedeutungslos, da 

diese Verformungen nach Wegfall der äußeren Kräfte völlig verschwinden. 



33

� Wesentlich für die Haftkraftverstärkung ist deshalb eine kombinierte 

elastisch-plastische Verformung des Partikelkontaktbereiches zu 

einem kleinen Platte-Platte-Kontakt aufgrund des Einwirkens der 

Haftkraft FH0 (siehe Gl.( 3.5)) selbst und einer zusätzlichen äußeren 

Normalkraft FN. Mit dem Kräftegleichgewicht des weichen Kontak- 

tes zweier steifer Partikeln 

( Ael 

+ A pl ) + FN 

− FW 

, el − pf 

A pl 

∑ F = 0 = FH 

0 + pVdW 

⋅ 

⋅ ( 3.71) 

folgt für die gesamte Haftkraft FH nach einigen Umrechnungen (sie- 

he ../../../Forschung/FLIESSEN/B_Theorie_FliessKW/Schüttec_- 

3_Kontakt_Theorie.doc#FHA_ges): 

folgt für die gesamte Haftkraft FH nach einigen Umrechnungen1 : 

κA 

FH = 

κ − κ 

⋅ FH 

0 + 

κ 

κp 

− κ 

⋅ FN 

= ( 1+ 

κ) 

⋅ FH 

0 + κ ⋅ FN 

( 3.72) 

H 

A 

H0 

p 

A 

( F F ) 

H0 

N 

p 

F = F + κ ⋅ + 

( 3.73) 

für Details siehe auch ..\..\Forschung\FLIESSEN\Berichte\Schüttec- 

_3_Sem_0.doc – Haftkraftgesneu, 

� Der elastisch-plastische Kontaktverfestigungskoeffizient κ 

κ = 

κ 

κp 

− κ 

( 3.74) 

A 

p 

enthält sowohl den charakteristischen dimensionslosen Kennwert ei- 

nes elastisch-plastischen Kontaktflächenverhältnisses κA (wobei 

AK = Ael + Apl) 

2 1 A pl 

κ A = + ⋅ 

3 3 A + A 

( 3.75) 

el 

pl 

� als auch den plastischen Repulsionskoeffizienten κp als Verhältnis 

des attraktiven VAN-DER-WAALS-Kohäsionsdruckes zur re- 

pulsiven plastischen Steifigkeit des Platte-Platte-Kontaktes eines 

Partikelpaares: 

pVdW 

C 

κp 

= = 

p 6 ⋅ π ⋅ a 

f 

H 

3 

F= 

0 

⋅ p 

f 



( 3.76) 

© Dr .- Ing.habil. J. Tomas 1992 

1 Diesem einfachen Modell liegen Versuche auf einer Zentrifuge mit einer engen Partikelgrößenklasse 

(Kalkstein, mittlere Partikelgröße dmi = 60 µm, pf ≈ 500 MPa, CH,svs = 15⋅10 -20 

J) zugrunde. Die Partikel wurden auf ein poliertes Stahlplättchen so aufgebracht, daß die 

Zentrifugalkraft zunächst als Anpreßkraft FN und anschließend nach Wenden als Abreißkraft 

FH wirkt. Bemerkenswert ist die lineare Zunahme der Haftkraft mit einer äußeren 

Normalkraft FN, die auf eine Verformung sehr kleiner Rauhigkeitserhebungen im nm- 

Bereich zurückzuführen ist. Bei stärkerer Anpressung werden auch größere Bereiche der 

Kontaktzone plastisch verformt. In diesem Fall ist die Zunahme der Haftkraft manchmal 

kleiner als im Anfangsteil. 

34

pf ≈ 3⋅σF 

plastischer Fließdruck (≈ 3⋅Fließgrenze für Zugbe- 

anspruchung), Oberflächenmikrohärte bzw. 

Partikelkontaktsteifigkeit 

� Grenzspannungsfunktion ist von der Summe der elastischen Ael, ir- 

∑ 

reversibel plastischen Apl und zeitabhängigen viskoplastischen 

(svw. viskosen) Avis Partikelkontaktdeformationen abhängig: 

H0 

VdW 

( Ael 

+ A pl + A vis ) − FN 

+ FW 

, el + pf 

⋅ A pl + ηs 

/ t A vis 

F = 0 = −F 

− p ⋅ 

⋅ 



( 3.77) 

� Gegenüber Gl.( 3.69) Einführung einer neuen erweiterten Haftkraft- 

gleichung zur Beschreibung der viskoplastischen Partikelkontakt- 

verfestigung infolge eingeprägter Normalkräfte FH0 und FN bei σ < 

100 kPa: 

H, 

ges 

H 

Ht 

( 1+ 

κ + κt 

) ⋅ FH 

0 + ( κ + κt 

) FN 

F = F + F = 

⋅ . ( 3.78) 

� Einführung einer zusätzlichen viskosen Kontaktrepulsion bzw. 

Kontaktverfestigung κt bei σ < 100 kPa (σa ≡ pVdW Kontaktfestig- 

keit, siehe auch siehe auch Gl.( 3.16): 

κ 

t 

σa 

= 

η ⋅ ε� 

V 

V 

pVdW 

≈ ⋅ t 

η ( T) 

s 

ηV Volumenviskosität (viskoplastische Steifigkeit), 

ε� Kontaktdeformationsgeschwindigkeitsgradient, 

V 

( 3.79) 

� Damit gilt für den Zusammenhang zwischen stationärer und instatio- 

närer innerer Reibung, siehe auch analoge Gl.( 3.104): 

tan st 

t 

it 

ϕ = ( 1+ 

κ + κ ) ⋅ tan ϕ ≠ f ( t) 

= const. 

( 3.80) 

� Umgerechnet auf einen Reibungswinkel (hier Anstiegswinkel des 

Zeitfließortes) ist: 

tan ϕi 

tan ϕ it = 

(3.81) 

tan ϕi 

⋅ pVdW 

⋅ t 

1+ 

tan ϕ ⋅ η 

st 

s 

( T) 

� Zusätzlich zu den 3 Kennwerten ϕi, ϕst, σ0 in der Gl.( 3.85), 2 neue 

physikalisch begründete Fließkennwerte: 

(1) ϕit innere Festkörperreibung versagender Partikelkontakte 

und 

σ = κ ⋅ σ dreiachsige Zugfestigkeit des Schüttgutes. 

(2) 0t 

t 0 

35

3.2.4 Partikelmechanische Pulvereigenschaften & Fließkennwerte 

• Zweiachsige Spannungszustände in einer gescherten Partikelpackung, 




• Zweiachsige Spannungszustände in einer gescherten Partikelpackung,ff 


• Grenzspannungsfunktionen bei Schüttgütern sind keine Materialkonstan- 

ten sondern Funktionen, und zwar = f(Zeit, Material, Partikelgröße, 

Feuchte, Temperatur usw. ...), siehe Folie F 3.76. 

• Typische Fließorte und Fließkennwerte für: siehe Folie F 3.77 

• Grenzspannungsfunktionen für beginnende Verfestigung, Fließen, kohäsives 

stationäres Fließen und Zeitverfestigung, siehe Folie F 3.78 

� Stationärer Fließort 

• Gewöhnlich als Gerade approximiert mit den Kennwerten: 

∗ ϕst stationärer innerer Reibungswinkel 

∗ σ0 dreiachsige Zugfestigkeit unverfestigter Partikelkontakte 

• Einhüllende aller Mohrkreise des stationären Fließens als kohäsives 

stationäres Fließen 

• weitestgehend unabhängig von der Vorverfestigung im Spannungsbereich 

1 ... 100 kPa 

� Erheblich einfachere Gleichung (als bei MOLERUS) für den stationärer 

Fließort, siehe F 3.76, erhalten. Mit dem linearen Stoffgesetz 

der lastabhängigen Haftkraft FH(FN), Gl.( 3.72), 

H 

( 1+ 

κ) 

⋅ FH 

0 + κ FN 

F = ⋅ , ( 3.72) 

der Grenzbedingung der Tangentialkraft im adhäsiven 

Partikelkontakt (Coulomb-Reibung) 

T, 

C, 

H 

i 

( 1+ 

κ) 

⋅( 

F F ) 

F = µ ⋅ + , ( 3.82) 

H0 

N 

sowie mit einem näherungsweise konstantem elastisch-plastischen 

Kontaktverfestigungskoeffizienten κ ≈ const., siehe Gl.( 3.74), und 

mit dem Mikro-Makro-Übergang der Kontaktkräfte in Spannungen, 

Gl.( 3.66), folgt eine bequeme lineare Gleichung des stationären 

Fließortes (Index st für stationäres Fließen) 

i 

( 1+ 

κ) 

⋅ ( σ + σ ) = tan ϕ ⋅ ( σ + ) 

τ = tan ϕ ⋅ 

σ 

0 

und als Radius-Mittelpunkt-Funktion σR,st = f(σM,st): 

( σ + ) 

R, st = sin ϕst 

⋅ M, 

st σ0 

st 

0 

( 3.83) 

σ (3.84) 

� Momentanfließort für beginnendes Fließen nach elastisch-plastischer 

Partikelkontaktverfestigung, Gl.( 3.71) und F 3.78: 

36

Fließort =ˆ individueller Fließort = Momentanfließort (yield locus): 

meist als Geradengl.( 3.60) approximiert mit den Kennwerten: 

∗ ϕi 

∗ τc Kohäsion 

∗ σZ 

∗ σc 

∗ σ1 

stationärem Fließen 

innerer Reibungswinkel 

Zugfestigkeit (dreiachsig) 

einaxiale Druckfestigkeit 

größte Hauptspannung beim Verfestigen, d.h. beim 

⎡ ⎛ sin ϕ ⎞ 

⎤ 

st 

sin ϕst 

= sin ϕ ⎢ ⎜ 

⎟ 

i ⋅ σM 

+ −1 

⋅ σM, 

st + ⋅ σ ⎥ ( 3.85) 

⎣ ⎝ sin ϕi 

⎠ sin ϕi 

⎦ 

σR 0 

oder vereinfacht mit der Gl.(3.84) des stationären Fließortes: 

σ R = sin ϕi 

⋅( 

σM 

− σM 

, st ) + σR 

, st 

( 3.86) 

Der Fließort hat einen positiven Anstieg (+ Vorzeichen vor σM bzw. 

σ), beginnt links im Punkt der isostatischen Zugfestigkeit σZ und en- 

det rechts im Mohrkreis des stationären Fließens σM = σM,st: 

σ 

⎛ sinϕ 

⎜ 

⎝ 

⎞ 

1⎟ 

⋅ σ 

⎠ 

sinϕ 

+ 

R, 

st 

st 

st 

σ Z = − σM, 

st = − M, 

st 

0 ( 3.87) 

sinϕ 

i sinϕ 

i 

sinϕ 

i 



⋅ σ 

Dementsprechend ist im τ = f(σ) – Diagramm, F 3.78: 

⎡ ⎛ sin ϕ ⎞ 

⎤ 

st 

sin ϕst 

= tan ϕ ⎢ ⎜ 

⎟ 

i ⋅ σ + −1 

⋅ σM, 

st + ⋅ σ ⎥ ( 3.88) 

⎣ ⎝ sin ϕi 

⎠ sin ϕi 

⎦ 

τ 0 

⎡ σR 

, st ⎤ 

= tan ϕi 

⋅ ⎢σ 

+ − σM, 

⎥ . ( 3.89) 

⎣ sin ϕi 

⎦ 

τ st 

� Verfestigungsort beinhaltet alle Spannungszustände, die zu einer 

Vorverfestigung - also Vorverdichtung und Konsolidierung - eines 

kohäsiven Schüttgutes führen, F 3.78: 

R 

i 

( − σM 

+ σiso 

) = sinϕ 

i ⋅ ( − σM 

+ σM, 

st ) + R, 

st 

σ = sinϕ ⋅ 

σ ( 3.90) 

⎡ ⎛ sinϕ 

⎞ 

⎤ 

st 

sinϕst 

= sin ϕi 

⋅ ⎢− 

σM 

+ ⎜ + 1⎟ 

⋅ σM, 

st + ⋅ σ ⎥ ( 3.91) 

⎣ ⎝ sinϕ 

i ⎠ sinϕ 

i ⎦ 

σR 0 

Dieser Verfestigungsort hat einen negativen Anstieg (- Vorzeichen 

vor σM bzw. σ), beginnt links im Mohrkreis des stationären Fließens 

σM = σM,st und endet rechts im Punkt des isostatischen Druckes σiso: 

σ 

⎛ sinϕ 

⎜ 

⎝ 

⎞ 

1⎟ 

⋅ σ 

⎠ 

sinϕ 

+ 

⋅ σ 

R, 

st 

st 

st 

σ iso = + σM, 

st = + M, 

st 

0 ( 3.92) 

sinϕ 

i sinϕ 

i 

sinϕ 

i 

Die Funktion τ = f(σ) ist, F 3.78: 

37

⎡ ⎛ sinϕ 

⎞ 

⎤ 

st 

sinϕst 

= tan ϕi 

⋅ ⎢− 

σ + ⎜ + 1⎟ 

⋅ σM, 

st + ⋅ σ ⎥ ( 3.93) 

⎣ ⎝ sinϕ 

i ⎠ sinϕ 

i ⎦ 

τ 0 

⎡ σR 

, st ⎤ 

= tan ϕi 

⋅ ⎢− 

σ + + σM, 

⎥ . ( 3.94) 

⎣ sinϕ 

i ⎦ 

τ st 

Mikroskopische Ursache dieser typischen makroskopischen Schütt- 

gutverfestigung sind die sich entwickelnden elastisch-plastischen 

Partikelkontaktverfestigungen gemäß Gl.( 3.71). 

� Zeitfließort, d.h. beginnendes Fließen nach zusätzlicher viskoplas- 

tischer Kontaktverfestigung, Gln. ( 3.77) und ( 3.78): 

∗ ϕit innerer Reibungswinkel 

∗ τct Kohäsion 

∗ σZt Zugfestigkeit 

∗ σct einaxiale Druckfestigkeit 

• charakterisiert zeitabhängige Verfestigung, wenn stationäres Fließen 

die Beanspruchungsvorgeschichte war 

• Verfestigungsspannung σ1 folgt damit aus Momentanfließort bzw. sta- 

tionärem Fließort, d.h. konstanter Druck während der Zeitverfestigung 

⎡ σR 

, st 

σRt = sin ϕit 

⋅ ⎢σMt 

+ 

⎣ sin ϕit 

⎤ 

− σM, 

st ⎥ 

⎦ 

( 3.95) 

und im τ = f(σ) – Diagramm ist, siehe Folie F 3.78: 

⎡ σR 

, st 

τt = tan ϕit 

⋅ ⎢σt 

+ 

⎣ sin ϕit 

⎤ 

− σM, 

st ⎥ . 

⎦ 

( 3.96) 

Der Verlauf o.g. Grenzspannungsfunktionen hängt folglich ab von 

• den granulometrischen Eigenschaften, 

• den Bedingungen und Stoffgesetzen der Kontaktverfestigung oder 

Haftkraftverstärkung der Partikel im Schüttgut und vor allem 

• von den Vorverfestigungsspannung σM,st sowie 

• von der Packungsdichte (Porosität). 

effektiver (oder wirksamer stationärer) Fließort (effective yield locus) 

• Tangente an Mohrkreise des stationären Fließens mit dem Kennwert: 

• ϕe effektiver - wirksamer - innerer Reibungswinkel 

• charakterisiert des kohäsionslose stationäre Fließen als eine vereinfachte 

wirksame Rechengröße 

• notwendig zur einfachen Berechnung der Silodrücke 

• folgt für σZ = 0 aus Gl.( 3.62) 

σR 

, st σ1− 

σ2 

sinϕ 

e = = 

( 3.97) 

σ σ + σ 

M, 

st 

1 

2 



38

• Seine Abhängig von der Mittelpunktsspannung σM,st lässt sich durch 

Einsetzen der Gl.(3.84) des stationären Fließorte in Gl.( 3.97) zeigen: 

( σ + σ ) 

sinϕ 

⎛ ⎞ 

st ⋅ M, 

st 0 

σ 

= ϕ ⋅ ⎜ 0 

sin ϕ = 

⎟ 

e 

sin st ⎜ 

1 + 

σ 

⎟ 

( 3.98) 

M, 

st 

⎝ σM, 

st ⎠ 

• Daraus gewinnt man mit Hilfe der Gl.( 3.127) 

Übung 

σ + σ 

1 0 

σ M, 

st + σ0 

= 

( 3.127) 

1 + sinϕst 

⎛ σ1 

+ σ0 

⎞ ⎛ σ1 

+ σ0 

⎞ 

⎜ 

⎟ ⎜ 

⎟ 

⎜ 1+ 

sinϕst 

⎟ ⎜ 1+ 

sinϕst 

sin ϕ 

= ϕ ⋅ 

⎟ 

e = sinϕst 

⋅ 

sin st 

⎜ σ1 

+ σ0 

⎟ ⎜ σ1 

+ σ0 

− σ0 

− σ0 

⋅sinϕst 

⎟ 

⎜ − σ0 

⎟ ⎜ 

⎟ 

⎝ 1+ 

sinϕst 

⎠ ⎝ 1+ 

sinϕst 

⎠ 

die Abhängigkeit des effektiven Reibungswinkels ϕe von der größten 

Hauptspannung σ1, siehe auch F 3.79: 

⎛ σ ⎞ 

1 + σ0 

sin ϕ ⎜ 

⎟ 

e = sin ϕst 

⋅ 

( 3.99) 

⎝ σ1 

− σ0 

⋅ sin ϕst 

⎠ 

Herleitung der Gleichungen für 

a) einaxiale Druckfestigkeit σ = ( σ bzw. 

τ , ϕ ) = ? 

c f Z 

c i 

Z 1 = f ( σZ 

bzw. 

τc 

, ϕi 

) 

b) einaxiale Zugfestigkeit σ 

= ? 

c) Tangentialpunkt σTa des σc-Kreises 

Zu a) einaxialer Spannungszustand, d.h. σ2 = 0 in Gl. ( 3.62) 

2sinϕi 

2 cosϕi 

σ c = σ1= 

⋅ σZ 

= 

1− 

sinϕ 

1− 

sinϕ 

τc 

( 3.100) 

i 

Zu b) Zugbereich, d.h. negative σ σ 1 = 0 und σ2 

= σZ1 

2sinϕ 

i 

2 cosϕ 

i 

i 

σ Z1 

= σ2 

= − σZ 

= − σZ 

( 3.101) 

1+ 

sinϕi 

1+ 

sinϕi 

Zu c) Tangentialpunkt σTa des σc-Kreises, siehe Bild 3.16: 

Dreieckswinkel: sin ϕ i 

σM 

− σTa 

= 

σ 

σ 

Ta 

= σ 

M 

− σ 

R 

⋅sin 

ϕ 

i 

Für die einaxiale Druckfestigkeit ist σ2 = 0 damit σR = σM = σc/2: 

σc 

σc 

σc 

σ Ta = − ⋅ sin ϕi 

= ⋅ ( 1− 

sin ϕi 

) 

2 2 2 

Nach Einsetzen von Gl.( 3.100) für σc folgt: 

2 ⋅ τc 

⋅ cos ϕi 

σ Ta = 

2 ⋅ 1− 

sin ϕ 

⋅ 1− 

sin ϕi 

= τc 

⋅ cos ϕ 

( 3.102) 

( ) ( ) i 

i 

Die Strecke von τc (auf der τ-Achse) entlang des Fließortes um den 

Betrag τc verlängert ergibt den Tangentialpunkt σTa des σc-Kreises. 



R 

39

Von hier das Lot auf den Fließort gezogen ergibt den Mohr- 

Kreismittelpunkt σM auf der σ-Achse. 

Bild 3.16: Spannungen 

und Fließkennwerte 

am linearen 

Fließort 

(kinematischer) Wandfließort (wall yield locus) 

• charakterisiert das stationäre Reibungsverhalten eines Schüttgutelementes 

an einer festen Wand 

• oft als Gerade approximiert mit den Kennwerten: 

∗ ϕw (kinematischer) Wandreibungswinkel 

∗ τa Adhäsion, falls vorhanden 

∗ σZ,W Zugfestigkeit, falls vorhanden 

• ansonsten ϕ W = arctan τW 

/ σW 

( 3.103) 

• abhängig von der Wandrauhigkeit, siehe auch F 3.79. 

Zusammenhänge zwischen den Reibungswinkeln in Partikelpackungen 

⇒ aus den Haftkraftbetrachtungen, siehe Abschnitt 3.1, folgen auch mathematisch-physikalische 

Zusammenhänge zwischen den Reibungswinkeln 

von Schüttgütern; Beispielsweise gelten folgende Abhängigkeiten der 

Reibungswinkel untereinander, siehe Bild F 3.79: 

• stationärer Reibungswinkel, allgemein gültige Definitionsgleichung 

( 1+ 

κ) 

⋅ tan ϕ = const. 

ϕ = 

( 3.104) 

tan st 

i 

• 

• κ = 0 ... 2 = f (HAMAKER-Konstante, Kontaktabstände, Partikelgröße 

1/d, Feuchte XW, ...), siehe auch Gl.( 3.3) 

innerer Reibungswinkel einer Zeitverfestigung ϕit für viskoplastisch 

fließende Materialien (Sinterbrücken), s. Zeitfließort Gl.( 3.16) 

• effektiver innerer Reibungswinkel ϕe, siehe Gl.( 3.99) oben 

Bild 3.17 einaxiale 

stationärer Fließort 

Druckfestigkeit beim τ 

kohäsiven 

ren Fließen 

stationä- 

ϕst 

σ 

σ 0 

ϕi 



τ 

σZ σ2= 0 σ1 

σZ,1 

τc 

σTa 

σR 

σM 

σ 

c, 

st 

Fließort 

σ 

2 ⋅ sin ϕst 

⋅ σ 

= 

1− 

sin ϕ 

st 

40 

0

• kinematischer Wandreibungswinkel ϕW 

⎪⎧ 

* 

* 

tan ϕ ⎛ ⎞ ⎡ ⎛ ⎞⎤⎪⎫ 

W tan ϕ 

h 

W 

r, 

W 

tan ϕW 

= tan ϕe 

⋅ ⎨ + ⎜ 

⎜1− 

⎟ 

⎟⋅ 

⎢1 

− exp ⎜ 

⎜− 

kr 

⋅ ⎟ 

⎟⎥⎬ 

( 3.105) 

⎪⎩ 

tan ϕe 

⎝ tan ϕe 

⎠ ⎣ ⎝ d50 

⎠⎦⎪⎭ 

* 

tan ϕ W Wandreibungsbeiwert für eine glatte Wand, F 3.79 

hr,W/d50 

bezog. Wandrauhigkeit 

hr,W mittlere Wandrauhtiefe 

kr Anpassungsfaktor 

Fließfunktion (nach Jenike, flow function) 



Bild 3.18: Wandrauhigkeiten 

• zur Charakterisierung der Fließfähigkeit von Schüttgütern 

ffc = σ1/σc bzw. ffct = σ1/σct ( 3.106) 

• für kohäsionsloses Gut ist τc = 0 ⇒ σc = 0 ⇒ ffc = ∞ 

• bei verhärtetem Gut ist während einer Lagerzeit t in Ruhe σct > σ1, 

d.h., das Gut zeigt zunehmend Festkörpereigenschaften 

• Verfestigungsfunktion von TiO2-Pulver, d50 = 0.61µm, Xw= 0.4%, 

Temperatur θ = 20 °C, siehe Folie F 3.80 

• Tabelle 3.1: Charakterisierung der Fließfähigkeit von Schüttgütern 

Werte Bewertung Beispiele 

10 ≤ ffc freifließend, rieselfähig trockener Sand 

4 ≤ ffc < 10 leichtfließend feuchter Sand 

2 ≤ ffc < 4 kohäsiv trockene Pulver 

1 ≤ ffc < 2 sehr kohäsiv, feuchte Pulver 

ffc < 1 nicht fließend, verhärtet ffc,t mit 

Festkörpereigenschaften 

Verfestigungs- oder Druckfestigkeitsfunktion 

gealterter Zement 

• ist im Sinne einer charakteristischen Konsolidierungsfunktion des 

Schüttgutes zu interpretieren. Aus den linearisierten Fließorten, Gln.( 

3.60) und (3.84) sowie Bilder F 3.76 folgt wiederum eine in den 

Spannungen lineare Funktion σc (σ1): siehe Folie F 3.81 

σ c = 

2 ⋅ ( sin ϕst 

− sin ϕi 

) 

1+ 

sin ϕ ⋅ 1− 

sin ϕ 


⋅ ( 1+ 

sin ϕi 

) 

⋅ σ1 

+ 

1+ 

sin ϕ ⋅ 1− 

sin ϕ 

⋅ σ ( 3.107) 

( ) ( ) 

st 

i 

( ) ( ) 0 

• Diese Druckfestigkeitsfunktion ( 3.107) läßt sich vereinfacht als Geradengleichung 

des Types schreiben: 

σ c= a1⋅ σ1+ 

σc, 

0 

( 3.108) 

• Die Druckfestigkeit des stationären Fließortes folgt mit ϕi ≡ ϕst aus der 

Gl.(3.84): 

st 

i 

41 

hr,W

2 ⋅ sin ϕ 

st 

σ c, 

st = ⋅ σ0 

( 3.109) 

1− 

sin ϕst 

⇒ Übung zur Überprüfung dieser Beziehung: 

Für ffc = 1 und σ 1 / ffc 

= σ1= 

σc, 

st folgen σ c, st = a1⋅ σc, 

st + σc, 

0 sowie 

σc, 

0 

σ c, 

st = und Gl.( 3.107) eingesetzt 

1− a1 

( ) 

( ) ( ) 

( ) 

( ) ( ) ⎥ 2⋅ 

1+ 

sin ϕi 

⋅ sin ϕst⋅ 

σ0 

σc, 

st = 

⎡ 2⋅ 

sin ϕ − ϕ ⎤ 

st sin i 

1+ 

sin ϕst 

⋅ 1−sin 

ϕi 

⋅ ⎢1 

− 

⎣ 1+ 

sin ϕst 

⋅ 1−sin 

ϕi 

⎦ 

2⋅ 

( 1+ 

sin ϕi 

) ⋅ sin ϕst⋅ 

σ0 

σc, 

st = 

⎡ 

( ) ( ) 

( 1+ 

sin ϕ ) ⋅ ( − ϕ ) − ⋅ ( ϕ − ϕ ) ⎤ 

st 1 sin i 2 sin st sin i 

1+ 

sin ϕst 

⋅ 1− 

sin ϕi 

⋅ ⎢ 

⎥ 

⎣ ( 1+ 

sin ϕst 

) ⋅ ( 1−sin 

ϕi 

) ⎦ 

2⋅ 

( 1+ 

sin ϕi 


σ0 

σ c, 

st = 

1+ 

sin ϕ −2⋅ 

sin ϕ −sin 

ϕ + 2⋅ 

sin ϕ −sin 

ϕ ⋅ sin ϕ 

st 

st 

st i st i 

2⋅ 

( 1+ 

sin ϕi 


σ0 

σ c, 

st = 

= 1+ 

sin ϕi−sin 

ϕst⋅ 

( 1+ 

sin ϕi 

) 

( 1+ 

sin ϕi 

) ⋅ ( 1−sin 

ϕst 

) 

= ( 1+ 

sin ϕ ) ⋅( 

1−sin 

ϕ ) 

2⋅ 

sin ϕ ⋅ σ 

i 



i 

1−sin 

ϕ + sin ϕ −sin 

⋅sin 

ϕ 

st 0 

σ c, 

st = 

q.e.d. ( 3.109) 

1−sin 

ϕst 

• Für Zeitverfestigungen folgt aus dem linearisierten Zeitfließort, Gl.( 

ct 

3.95), ebenfalls eine in den Spannungen lineare Funktion σct(σ1): 

2 ⋅ ( sin ϕst 

− sin ϕit 

) 

( 1+ 

sin ϕ ) ⋅ ( 1− 

sin ϕ ) 

st 

it 

1 

i 


⋅ ( 1+ 

sin ϕit 

) 

⋅ σ0 

t 

( 1+ 

sin ϕ ) ⋅ ( 1− 

sin ϕ ) 

σ = 

⋅ σ + 

( 3.110) 

Böschungswinkel 

• Für kohäsionsloses Schüttgut gilt ϕ i ≈ϕe 

≈ϕst 

≈ϕB 

als Böschungswinkel 

⇒ ϕ ≠ϕ 

≠ϕ 

⇒ gewöhnlich abhängig von der Meßmethode 

• B1 

B2 

B3 

ϕB1 

Aufschütten 

eines Kegels 

ϕB2 

Auslaufen aus einem Behälter 

mit horizontalen Boden 

st 

st 

st 

it 

i 

ϕB3 

42 

Rotation eines zylindri- 

schen Behälters 

Bild 3.19: Auftreten statischer oder dynamischer Böschungswinkel 

• bei kohäsivem Schüttgut ist ϕB ≈ ϕe in grober Näherung bei einer gleiten- 

den Böschung; ansonsten nur für kohäsionslose Schüttgüter reproduzier- 

bar meßbar!

3.2.5 Kompressionsfunktionen, Schüttgut- und Packungsdichte 

• Lückenvolumenanteil: 

VLücke 

V − Vs 

ε = = = 1− 

ϕs 

V V 

ρb 

= 1− 

ρ 

( 3.111) 

ϕs Feststoffvolumenanteil 

• Schüttgutdichte ρb = m/V 

⇒ bei sehr lockerer Lagerung Schüttdichte ρb,0 

• Feststoffdichte ρs 

• Einaxiale Verdichtung eines kompressiblen Schüttgutes, siehe F 3.82 

Die Kompressibilität bei Schüttgütern entspricht der Druckabhängigkeit 

der Packungsdichte und wird beeinflußt von folgenden Mikrovorgängen: 

(1) Umlagerung steifer Partikeln mit steifen Kontakten zu einer dichteren 

Zufallspackung, 

(2) Deformation weicher Kontakte von harten (mineralischen) Partikeln 


(3) Deformation weicher Partikeln (z.B. Biozellen), 

(4) Partikelzerkleinerung. 

Die oben beschriebenen empirischen Funktionen lassen sich auch aus einer 

physikalisch begründeten Beschreibung des Deformations- bzw. Kompressionsverhaltens 

gewinnen: 

∆l 

1 

1) analog HOOKschem-Gesetz für Festkörper = ε = ⋅ ∆σ 

bzw. 

l0 

E 

∆x 

1 

= γ = ⋅ ∆τ 

mit E = 2( 

1+ 

ν) 

⋅ G 

( 3.112) 

y G 

0 



s 

2) bei Flüssigkeiten und auch Festkörpern gilt für dreiachsigem Druck: 

dV 

V0 

dp 

= κ = 

( 3.113) 

K 

κ Kompressibilität (hier dimensionslos definiert! - im Unterschied 

zu κ =1/K siehe HÜTTE S. B 191) 

K Kompressionsmodul, = Kompressionswiderstand oder Steifigkeit, 

im isotropen Fall gilt 

( 1−2ν) 

K 

E = 3⋅ 

⋅ 

( 3.114) 

/ ε ε − = ν Querdehnungs- o. POISSON-Zahl, 

quer 

axial 

für inkompressible, volumenerhaltende Stoffe ist maximal 

ν = 0,5 und für ν = 0 ist K ≅ E/3 

3) für Gase bei adiabatischer (isentroper) Zustandsänderung (= kein Wärmeaustausch 

mit der Umgebung, S = const., gültig insbesondere für 

schnelle Druckänderungen z.B. infolge Schallwellen): 

43

p⋅ 

V 

κad 

κad 

= 

const. 



( 3.115) 

Isentropen- oder Adiabatenexponent (κad = 5/3 ≈ 1,66 für ein- 

atomige bzw. κad = 7/5 = 1,4 für zweiatomige Gase) 

Damit folgt (- Vorzeichen für Verdichtung kann entfallen): 

dV κ 1 const. 

ad − 

κad 

V = − − 2 

dp 

p 

dV 

dp 

bzw. 

1 const. 

V 1 V 

= = 

( 3.116) 

κ ad κ pV 

p κ p 

ad 

dV 

V 

ad 

1 1 dp 

≡ κ = ⋅ dp ≡ D.h. 

κ p K 

ad 

RT 

K = κad 

p = κad⋅ 

( 3.117) 

V 

m 

Ein hoher Adiabatenexponent bedeutet eine geringe Kompressibili- 

tät, d.h. die höchste Kompressibilität tritt beim idealen Gas κad = 1 

auf. 

4) Kompression eines Schüttgutes 

Analog zur adiabaten Gaskompressibilität Gl.( 3.116) ist: 

dV 1 V d( 

V / m) 

1 

− = bzw. − = 

dp κad 

p 

dp κad 

V / m 

p 

Für die linke Seite ist: 

d( 

1/ 

ρb 

) dρb 

− = − 2 

dp − ρb 

⋅ dp 

eingesetzt folgt: 

dρb 

1 

= n ⋅ 

2 

ρb 

⋅ dp ρb 

⋅ p 

oder 

dρb ρb 

= n ⋅ 

dp p 

n ≡ 1/ 

κ wurde eine gutabhängige Konstante – hier der sog. 

Mit ad 

Kompressibilitätsindex – eingeführt. Wenn man zusätzlich die Van- 

der-Waals-Gleichung von Gasen, die nahe des Kondensationspunktes 

gilt, beachtet (Vm molares Volumen), 

2 

( a / V ) ⋅( 

V − b) 

= R ⋅T 

+ ( 3.118) 

p VdW m m 

lässt sich nun der Schüttgutdruck durch die mittlere Verfestigungsnormalspannung 

plus Haftspannung ausdrücken p = σM, 

st + σ0 

: 

dρ 

ρ 

b 

b 

= n ⋅ 

dp 

p 

dσ 

= n ⋅ 

σ + σ 

0 

M, 

st 

M, 

st 

( 3.119) 

• Diese Differentialgleichung einer inkrementellen „Verdichtungsge- 

schwindigkeit“ wird auch als Kompressionsrate bezeichnet, s. F 3.83: 

dρ 

dσ 

b = n 

M, 

st 

⋅ 

σ 

0 

ρb 

+ σ 

M, 

st 

Mit der Randbedingung ρb = ρb,0 wenn σM,st = 0 ist: 

( 3.120) 

44

ρ 

b 

∫ 

dρ 

ρ 

b 

= n ⋅ 

σ 

M , st 

ρb 

, 0 b 

0 0 M, 

st 

∫ 

σ 

dσ 

n 

M, 

st 

b b, 

0 1 ⎟ 

0 

⎟ 

⎛ σ ⎞ 

= ρ ⋅ ⎜ + 

σ 

M, 

st 

+ σ 

ρb 

d.h. ln = n ⋅ [ ln( 

σ + σ ) − ln σ ] 


ρ 

b, 

0 


0 

M, 

st 

ρ ( 3.121) 

⎝ ⎠ 

Eine sehr hohe Kompressibilität - analog einem idealen Gas - wäre 

folglich bei n = 1 zu beobachten, wobei hier der Kompressions- 

widerstand oder die Steifigkeit der Packung am niedrigsten ist. Bei in- 

kompressiblen Gut wäre die Steifigkeit unendlich. 

Bild 3.20: Darstellung 

der 

Kompressionsfunktion 

nach 

Gl.( 3.121) 

Schüttgutdichte 

ρb 

σ0 

ρb,0 

Der Exponent n lässt sich als Kompressibilitätsindex physikalisch 

sinnvoll interpretieren. Kohäsive Pulver haben bei geringen Verfestigungsspannungen 

σ1 < 100 kPa meist Werte um n ≈ 0,1 (siehe Tabelle 

3.2): 

Tabelle 3.2: Charakterisierung der Kompressibilität von Schüttgütern 

n = 1/ 

κ = 3/5 = 0,6; 5/7 = 0,71) 

(Vergleiche ad 

Kompressibilitätsindex Bewertung Beispiele 

0 ≤ n < 0,01 inkompressibel trockener Sand 

0,01 ≤ n < 0,05 wenig kompressibel feuchter Sand 

0,05 ≤ n < 0,1 kompressibel kohäsive Pulver 

0,1 ≤ n < 1 sehr kompressibel sehr kohäsive Pulver 

Für kohäsive Schüttgüter ist nun die Verwendung dieser 

dreiparametrigen Funktion Gl.( 3.121) ratsam: 

� mit zusätzlicher Berücksichtigung eines meßbaren Ordinatenab- 

= ρ , 

schnittes, für σM,st = 0 ist b b, 

0 ρ 

0 

n = 1 ideal kompressibel 

0 < n < 1 kompressibel 

n = 0 inkompressibel 

mittlere Verfestigungsspannung σM,st 

� und einem Abzissenabschnitt im negativen Zugspannungsbereich, 

für b 0 = ρ ist σM,st = - σ0. 

Für den Zusammenhang zwischen dem mittleren Druck σM,st und der 

Normalspannung beim Anscheren σAn gemäß der Gl.( 3.122) ist die 

Verdichtungsfunktion: 

0 

45

σM 

, st 1 ⎛ σ ⎞ An 

1 + = 

⋅ 

⎜ 

⎜1+ 

⎟ 

( 3.122) 

σ0 

1− 

sin ϕi 

⋅sin 

ϕst 

⎝ σ0 

⎠ 

ρ 

ρ 

b 1 

b, 

0 

⎛ 1 

= 

⎜ 

⎝1− 

sin ϕi 

⋅sin 

ϕ 

st 

⎞ 

⎟ 

⎠ 

n 

⎛ 

⋅ 

⎜ 

⎝ 

σ 

+ 

σ 


An 


0 

⎞ 

⎟ 

⎠ 

n 

( 3.123) 

Diese Verdichtungs- oder Kompressionsfunktion, Gl.( 3.121), lässt 

sich auch durch Ersetzen von σM,st mittels der größten Hauptspan- 

nung σ1 berechnen: 

Die größte Hauptspannung σ1 ist am MOHR-Kreis des stationären 

Fließens: 

σ1 

− σ2 

σ1 

+ σ2 

σ 1 = + = σR 

, st 

2 2 

+ σM, 

st 

(3.124) 

Ersetzen der Radiusspannung σR,st mit Hilfe der Gl.(3.84) des statio- 

nären Fließortes 

σ R, st = sin ϕst 

⋅( 

σM 

, st + σ0 

) 

(3.84) 

und es folgt Umrechnung σ1 = f(σM,st): 

( σ + σ ) + st 

1 = sin ϕst 

⋅ M, 

st 0 σM, 

σ (3.125) 

1 

M, 

st 

( 1+ sin ϕst 

) + sin ϕst 

⋅σ 

0 

σ = σ ⋅ 

(3.126) 

Addieren von σ0 auf beiden Seiten der Gleichung liefert: 

σ + σ = σ ⋅ 1+ sinϕ 

+ sinϕ 

⋅ σ + σ = σ ⋅ 1+ 

sinϕ 

+ σ ⋅ 1+ 

sinϕ 

1 

1 

0 

σ + σ 

0 

= 

M, 

st ( st ) st 0 0 M, 

st ( st ) 0 ( st ) 

( 1 + sinϕ 

) ⋅ ( σ + σ ) 

st 

σ + σ 

M, 

st 

0 

1 0 

σ M, 

st + σ0 

= 

( 3.127) 

1+ sin ϕst 

Einsetzen von Gl.( 3.127) in Gl.( 3.121) liefert die Verdichtungsfunk- 

tion als Funktion ρb = f(σ1), wie sie für die Trichterauslegung be- 

nutzt wird: 

ρ 

ρ 

b 1 0 

= 

= 

⋅ 1 

b, 

0 

ρ 

ρ 

b, 

0 

⎛ 

⎜ 

⎝ 

( 1+ 

sin ϕ ) 

n 

σ + σ ⎞ 

⎟ 

st ⋅σ 

0 ⎠ 

⎛ 1 

⎜ 

⎝1+ 

sin ϕ 

b = 

1 

st 

⎞ 

⎟ 

⎠ 

n 

⎛ 

⋅ 

⎜ 

⎝ 

σ 

+ 

σ 

⎛ 1 

⎜ 

⎝1+ 

sin ϕ 

1 

0 

⎞ 

⎟ 

⎠ 

n 

st 

⎞ 

⎟ 

⎠ 

n 

⎛ 

⎜ 

⎝ 

σ 

+ 

σ 

1 

0 

n 

⎟ ⎞ 

⎠ 

( 3.128) 

Dies kann man auch mit einer modifizierten Schüttgutdichte der lo- 

ckeren unverfestigten Packung ρb,0* ausdrücken: 

n 

* ⎛ 1 ⎞ 

ρ b, 

0 = ρb, 

0 ⋅ ⎜ 

1 sin ⎟ 

(3.129) 

⎝ + ϕst 

⎠ 

n 

* 

1 

b b, 

0 1 ⎟ 

0 

⎟ 

⎛ σ ⎞ 

= ρ ⋅ ⎜ + 

σ 

ρ . ( 3.130) 

⎝ ⎠ 

46

Für den Zusammenhang zwischen dem mittleren Druck σM,st und dem 

isostatischen Druck σiso gemäß der Gl. (3.131) ist die Kompressions- 

funktion: 

sin ϕ ⋅σ 

+ sin ϕ ⋅σ 

sin ϕ ⋅ 



( σ + σ ) 

i iso 

i 0 

i iso 0 

σ M, 

st + σ0 

= 

= 

(3.131) 

sin ϕst 

+ sin ϕi 

sin ϕst 

+ sin ϕi 

ρ 

ρ 

sin ϕi 

⋅( 

σiso 

+ σ0 

) 

( sin ϕ + sin ϕ ) ⋅σ 

b i 1 

b, 

0 

ρ 

ρ 

⎛ 

= 

⎜ 

⎝ 

st 

b i 1 

b, 

0 

⎛ sin ϕ ⎞ 

= 

⎜ 

sin st sin ⎟ 

⎝ ϕ + ϕi 

⎠ 

i 

n 

0 

⎛ 

⋅ 

⎜ 

⎝ 

kohäsionsloses Schüttgut: 

⎞ 

⎟ 

⎠ 

n 

⎛ sin ϕ ⎞ 

= 

⎜ 

sin st sin ⎟ 

⎝ ϕ + ϕi 

⎠ 

σ 

+ 

σ 

iso 

0 

⎞ 

⎟ 

⎠ 

n 

n 

⎛ 

⋅ 

⎜ 

⎝ 

σ 

+ 

σ 

iso 

0 

⎞ 

⎟ 

⎠ 

n 

( 3.132) 

Für ein kohäsionsloses Schüttgut σ0 = 0 liefert diese Herleitung nun 

auch die physikalische Plausibilität einer ursprünglich empirisch aufgestellten 

Gleichung Gl.( 3.133). Mit den Randbedingungen ρb = 0 

wenn σ1 = 0 und ρb = ρs/2 wenn σ1 = σ1/50 folgt: 

ρb 

σ1 

dρb 

dσ1 

ρb 

σ1 

∫ = n ⋅ 

ρ ∫ d.h. ln = n ⋅ ln 

σ 

ρ / 2 σ 

ρs 

/ 2 b σ1 

/ 50 1 

s 

1/ 

50 

n 

1 ⎛ ⎞ 

1 

1 ⎜ 

σ 

− ε = ⋅ ⎟ 

2 ⎜ σ ⎟ 

1, 

50 

( 3.133) 

⎝ ⎠ 

− wird nahezu die kubische Packung erreicht: 

1 − ε = π = 0, 

5236 

6 

σ1 = σ1,50, wenn 1 ε = 0, 

5 

• spezifische Kompressionsarbeit eines kohäsiven Schüttgutes 

Die Arbeit beim Verdichten ist entlang des Stempelweges s oder bezüg- 

lich einer Volumenverminderung – dV: siehe Folie F 3.84 

W = F( 

s) 

ds = − p dV 

( 3.134) 

∫ 

∫ 

und massebezogen kann man schreiben mit ( ) 2 

d 1/ 

ρ = −dρ 

/ ρ : 

dV 

1 p( 

ρ) 

m = −∫ 

p( 

V) 

= −∫ 

p( 

V) 

d = ∫ dρ 

m 

ρ ρ 

( 3.135) 

W 2 

Zweckmäßig sollte Wm = f(p) ausgedrückt werde. Für das Schüttgut sei 

mit der Kompressionsrate nach Gl.( 3.120): 

ρb 

dρ 

b = n ⋅ ⋅ dp 

p 

p( 

ρb 

) 

W m, 

b = ∫ dρ 

2 b 

ρb 

p( 

ρb 

) ρb 

dp 

= ∫ n ⋅ ⋅ dp = n ⋅ 

2 

ρ ∫ 

b p ρb 

( 3.136) 

dp 

W m, 

b = n ⋅∫ 

ρ 

( 3.137) 

b 

Mit der Gl.( 3.121) der Schüttgutdichte ist also: 

W 

m, 

b 

σM 

, st 

= n ⋅ ∫ 

0 

1 

ρ 

b, 

0 

⎛ σ 

⋅ ⎜ 

⎝ 

0 

+ σ 

σ 

0 

M, 

st 

⎞ 

⎟ 

⎠ 

−n 

dσ 

M, 

st 

( 3.138) 

47

wobei 

W 

m, 

b 

z 

σ 

+ σ 

0 M, st 

= und d M, 

st = σ0 

⋅ dz 

σ0 

σM 

, st 

= n ⋅ ∫ 

0 

σ 

ρ 

0 

b, 

0 

⋅ 

( z) 

−n 

σ mit n ≠ 1: 

n σ 

dz = ⋅ 

1− 

n ρ 

1−n 


b, 

0 


0 

⎛ σ 

⋅ ⎜ 

⎝ 

0 

+ σ 

σ 

0 

M, 

st 

⎞ 

⎟ 

⎠ 

1−n 

σM 

, st 

0 

1−n 

n σ0 

Wm, 

b = ⋅ 

1− 

n ρb, 

0 

⎛ σ0 

+ σM, 

st ⎞ 

⋅ ⎜ 

⎟ 

⎝ σ0 

⎠ 

n σ0 

− ⋅ 

1− 

n ρb, 

0 

⎛ σ ⎞ 0 ⋅ ⎜ 

⎟ 

⎝ σ0 

⎠ 

1−n 

n σ ⎡⎛ 

σ + σ ⎞ ⎤ 

0 0 M, 

st 

W ⋅ ⋅ ⎢ 

⎜ 

⎟ 

m , b = 

−1⎥ 

1− 

n ρb, 

0 ⎢⎣ 

⎝ σ0 

⎠ ⎥⎦ 

( 3.139) 

Vereinfacht lässt sich auch näherungsweise mit 1 – n ≈ 1 schreiben: 

1 

σ ⎡⎛ 

σM, 

st ⎞ ⎤ σ 

0 

M, 

st 

Wm, 

b ≈ n ⋅ ⋅ ⎢ 

⎜ 

⎜1+ 

⎟ −1⎥ 

= n ⋅ 

ρb, 

0 ⎢ 0 ⎥ ρb, 

0 

⎣⎝ 

σ ⎠ ⎦ 

( 3.140) 

• spezifische Kompressionsarbeit eines kohäsionslosen Schüttgutes 

dp 

W m, 

b = n ⋅∫ 

ρ 

( 3.137) 

b 

Mit der Gl.( 3.133) der Schüttgutdichte ist also: 

σ 

−n 

1 

2 ⎛ σ ⎞ 1 

Wm, 

b = n ⋅ ∫ ⋅ ⎜ 

⎟ 

ρ 0 s ⎝ σ1/ 

50 ⎠ 

dσ1 

σ1 

wobei z = 

σ 

und dσ 1 = σ1/ 

50 ⋅ dz mit n ≠ 1: 

W 

W 

m, 

b 

m, 

b 

1/50 

σ1 

σ 

= 2n 

⋅ ∫ ρ 

0 

2 ⋅ n 

1− 

n 

1/ 

50 

s 

σ 

ρ 

⋅ 

( z) 

−n 

2 ⋅ n σ 

dz = ⋅ 

1− 

n ρ 

1/ 

50 

1−n 

1/ 

50 

s 

⎛ σ 

⋅ ⎜ 

⎝ σ 

1 

1/ 

50 

⎞ 

⎟ 

⎠ 

1−n 

σ1 

0 

( 3.141) 

1/ 

50 1 

= ⋅ ⋅ 

( 3.142) 

s 

⎛ σ 

⎜ 

⎝ σ 

⎞ 

⎟ 

⎠ 

Vereinfacht lässt sich auch näherungsweise mit 1 – n ≈ 1 schreiben: 

σ ⎛ 1/ 

50 σ ⎞ 1 σ1 

Wm, 

b ≈ 2 ⋅ n ⋅ ⋅ ⎜ 

⎟ = 2 ⋅ n ⋅ 

ρs 

⎝ σ1/ 

50 ⎠ ρs 

( 3.143) 

Beispiele für Fließparameter von Schüttgütern 

a) trockenes kohäsionsloses Gut ϕ i = ϕe 

= ϕst 

, siehe Bild F 3.77 

b) allgemeiner Fall eines kohäsiven Gutes 

- Anzahl von genannten Kennwerten zur Beschreibung des Fließverhal- 

tens notwendig 

c) nasses plastisches Gut, im allgemeinen gilt: 

n 

τ = τo 

+ ηP 

⋅ γ� 

( 3.144) 

ηP Plastizität 

du 

dy 

48

γ� = du / dy Schergeschwindigkeitsgradient, siehe Folie F 3.69 

n < 1 strukturviskoses Verhalten 

n = 1 linear viskoplastisches Verhalten 

n > 1 dilatantes Verhalten 



Bild 3.21: Fließkurven 

mit Festkörperreibungsanteil: 

τ= tanϕ ⋅ ( σ+ 

σ ) + η 

n 

⋅ γ� 

( 3.145) 

i 

Z 

P 

mit Term für Partikelkollisionen 

τ= tanϕ ( σ + σ ) + η 

n 

⋅ γ� 

+ a 

2 2 

⋅ρ 

⋅d 

⋅γ� 

( 3.146) 

i 

d Partikelgröße, 

aK 

τ 

Z 

Materialparameter 

P 

3.3 Messung der Fließeigenschaften von Schüttgütern 

3.3.1 Übersicht der Meßgeräte 

K 

b 

• Schnelltests zur Quantifizierung der Mechanischen Eigenschaften kohä- 

siver Pulver, siehe Folie F 3.85 

• Schergeräte zur Messung der Fließeigenschaften kohäsiver Schüttgüter, 

1) Direktschergeräte 

Translationsscherzelle (Jenike-Scherzelle), siehe F 3.87 


⇒ direkte Messung der Scher- und Normalspannungen, siehe F 3.88 

⇒ geeignet zur Messung aller genannten Fließkennwerte 

⇒ Wandreibungsmessung mit Anordnung b) 

⇒ Zeitverfestigungsmessung mit Anordnung a) und einem Zellensatz 

⇒ nachteilig: verhältnismäßig hoher zeitlicher Meßaufwand von etwa 

3 ... 5 Tagen 

n>1 

n=1 

n

⇒ nachteilig: ungeeignet für Messung Zeitverfestigungen 

direkte Schergeräte meist für Drücke σ = 1 ... 50 kPa ausgelegt 

2) indirekte Schergeräte 

f) Triaxialgerät 

⇒ üblicher in der Bodenmechanik, für σ > 50 kPa 

⇒ direkte Messung der Hauptspannungen, F 3.88 

⇒ nachteilig: aufwendige Probenpräsentation 

dazu gehört auch sog. Biaxialbox 

3) einachsiger Druckfestigkeitstest 

⇒ Ergänzung der Schergeräte für höhere Festigkeitsbereiche, F 3.89 

⇒ direkte Messung der Druckfestigkeit insbesondere bei Zeitverfesti- 

gungen τt > 50 kPa 

⇒ Vergleich der mittels Scherzelle und einaxialen Druckfestigkeits- 

test gemessenen Druckfestigkeiten, F 3.89 

3.3.2 Meßmethodik eines direkten Scherversuches 

Fließen von Schüttgütern unterteilt in: 

• sog. beginnendes (instationäres) Fließen, siehe Folie F 3.90 

• überverfestigte Proben 

• Fließen unter Auflockerung ρb↓, ε↑, Dilatanz 

• FS erreicht ein Peak 

• sog. stationäres Fließen, 

• kritisch verfestigte Probe (durch geeignete Vorverfestigunglasten 

und Einbringen von Scherspannungen durch Drehschwingungen 

des Deckels erreichbar) 

• Fließen unter Volumenkonstanz, dV = 0, ρb = const., ε = const. 

• FS = const. 

• elastische Deformation, 

• unterverfestigte Proben 


• 

• allmählicher Übergang zum plastischen Fließen mit ständiger Verdichtung, 

ρb↑, ε↓ 

• Anstieg von FS bis zum Erreichen des stationären Fließens, F 3.92 

Ausmessen eines Fließortes, Erläuterung der beiden Diagramme, F 

3.93, F 3.94, FS = f(s) 

→ Anscheren bis zum konstanten Scherkraft-FS-Verlauf bei 

σ An = FN , An A , liefert τ An = FS, An A 

→ Abscheren unter verminderter Normallast σ Ab = FN , Ab A , liefert 

τ A als Maximalwert (Peak) 

Ab = FS , Ab 



50

→ Mittelung der Anscherwerte einschl. Berechnung des 

Fehlerintervalles (Vertrauensbereich bei 95 %iger statistischer Sicherheit), 

τ An 

( 3.147) 

= τAn⋅ 

( 1± ∆τAn 

/ τAn 

) 

→ wobei der Fehlerbereich (hier Konfidenzintervall der Normalverteilung) 

aus der Standardabweichung der mehrfach gemessenen (n ≈ 8 

... 12) Anscherwerte abgeschätzt wird: 

∆ τ ≈1, 

96⋅ 

s 

( 3.148) 

An τAn 

→ Ausgleich der Abweichungen der gewöhnlich doppelt gemessenen 

Abscherwerte τAb,gem infolge Schwankungen der Anscher- und 

Schüttgutdichtewerte durch einfache Meßwertekorrektur mit 

Anschermittelwert: 

τ = τ ⋅ τ / τ 

( 3.149) 

Ab , korr 

Ab, 

gem 

An 

An, 

gem 

→ Gültigkeit der Meßpunkte beachten; Meßpunkte nur gültig, wenn 

rechts des Tagentialpunktes des σc -Kreises gelegen 

→ Ermittlung der gefüllten Zellenmasse zur Berechnung der Schüttgutdichte 

ρ = m − m V 

( 3.150) 

b 

( Zelle ) Zelle 

• Gewinnung des σ1-Kreises 

• punkteweises Auftragen der Einzelmeßwerte und Verbinden durch eine 

dünne Gerade, siehe Folie F 3.92 

• Suche des Mittelpunktes des σ1 -Kreises dergestalt, daß Kreis durch 

den Anscherpunkt A geht und die gewonnene Gerade tangiert (und 

nicht schneidet!), Ablesen σ1 und σ2 

• 

• Zeichnen einer Tangente an den σ1-Kreis durch den Ursprung mit ϕe 

als Anstieg 

Ausmessen des Anstieges ϕi - des Fließortes 

• Suche des Mittelpunktes des σc-kreises dergestalt, daß der Kreis durch 

den Ursprung geht ( σ2 = 0!) und den Fließort tangiert, liefert σc, Berechnung 

ffc 

• Wiederholung für alle gemessenen Fließorte 

• Ermittlung der Kennwerte des stationären Fließortes, siehe F 3.81 

• Berechnung der Radiusspannung σ R, 

st = ( σ1 

− σ2 

) / 2 und Mittelpunktsspannung 

σ = ( σ + σ ) / 2 der Mohr-Kreise für stationäres 

M, 

st 

1 



2 

Fließen 

• Einzeichnen in einem σR,st - σM,st - Diagramm und Verbinden zu einer 

Geraden 

• Ermittlung von ϕst aus dem Anstieg α und σ0 aus dem negativen 

Abzissenabschnitt 

ϕ st = arcsin(tan α) 

( 3.151) und 0 Z σ = σ ( 3.152) 

51

• Messung der Wandreibung 

• kinematische bzw. stationäre Wandreibung, siehe Folie F 3.94 

τW 

τa 

σZW 

WFO 

ϕW* 

σW 



52 

Bild 3.22: kine- 

matischeWand- reibung 

→ damit Simulation des Abgleitens von Schüttgutschichten entlang 

der Wand, z. B. im Silotrichter bei abnehmendem Druck 

⇒ Gleitreibung simuliert 

• instationäre Wandreibung 

→ Versuchsmethodik wie beim Versuch zur Messung der inneren 

Reibung mit Anscheren und Abscheren, z. B. 

→ auch als Zeitverfestigungsversuch auf der Wandprobe machbar 

liefert in den meisten Fällen eine Adhäsion τa bzw. die Zugfestigkeit 

σzw beim Auftragen in einem separaten τ - σ -Diagramm: 

τ 

FS 

bzw. 

τ 

FS 

bzw. 

τ 

WFO 

ϕW 

Bild 3.23: instationäre 

Wandreibung 

Bild 3.24: 

Wandfließort 


Mohrkrei 

s 

aber man beachte: Wandreibungswinkel ϕw wird immer aus dem aktuellen 

Verhältnis τW/σW gebildet, siehe Bild 3.24. 

τ 

σ2 

Verminderung von σ während 

des Schervorganges 

unabh. von ρb! 

σ = const σ ↓ 

s 

τW 

σW 

W 

ϕ W = arctan ( 3.153) 

σW 

s 

σ1 

σ 

Bild 3.25: Wandfließort mit Adhäsion

• Wandfließort ist meist eine Gerade bei Stahl u. Metallen 

• Wandfließort ist eine Kurve bei Plastbeschichtungen 

Messung von Zeitverfestigungen 

• Anscheren wie beim Fließort, welcher die größte Hauptspannung σ1 

beim Verfestigen (Beanspruchungsvorgeschichte ist immer statio- 

näres Fließen!) liefert, F 3.93, 

• Aufbewahren der Proben unter der Last σt = σ1 ! eine gewisse Zeit (z. 

B. Wochenende) unter den simulierten Umgebungsbedingungen hin- 

sichtlich Temperatur, Feuchte usw., F 3.94 

• Abscheren unter einer gewissen Normallast σ, die durchaus σ > σAn 

sein kann ⇒ hängt von der Art, der sich einstellenden Festkörperbrü- 

cken ab, 

3.3.3 Numerische Versuchsauswertung 

• Auswahl numerischer Berechnungsgleichungen, siehe Folie F 3.81 

• lineare Regression der Fließorte mit allen Abscherpunkten τab,i, ohne 

Anscherpunkte τAn,i 

• Berechnung der einaxialen Druckfestigkeit σc 

Überprüfung der Gültigkeit der Meßpunkte, d.h. σ i > τc 

⋅cosϕ 

i 

→ ansonsten Meßwert verwerfen u. nochmals lineare Regression, 

• Berechnung der größten Hauptspannung beim Verfestigen σ1 

• Ermittlung des effektiven Reibungswinkels ϕe 

• Berechnung der kleinsten Hauptspannung σ2 

• Berechnung der Radius- und Mittelpunktsspannungen σR, σM 

• lineare Regression des stationären Fließortes 

• Ermittlung des stationären Reibungswinkels ϕst 

• Ermittlung der isostatischen Zugfestigkeit σ0 der unverfestigten Kon- 

takte 

• Berechnung der Schüttgutdichte der lockeren Packung ρb,0 und des 

Kompressibilitätsindexes n in den Funktionen ρb = f(σ1) 

→ gehört zum Kennwertediagramm 

3.3.4 Anscherarbeit 

• Kompressions- und Anscherarbeit, siehe Folie F 3.95 

3.4 Fließkennwerte kohäsiver Schüttgüter und deren Beeinflussung 

3.4.1 Wesentliche Fließkennwerte kohäsiver Pulver 



ab, 

53

• Auftragung der wichtigsten Fließkennwerte als Funktion der Verfesti- 

gungshauptspannung σ1, F 3.96 

→ stellen Material"gesetze" bzw. Stoffgesetze dar, d.h. invariant ge- 

genüber gewählter Meßtechnik, -methodik und Koordinatensyste- 

me 

→ sind aber Funktionen, und zwar von 

• Feuchte • Partikelgrößenverteilung 

• Lagerzeit • chem.-min. Zusammensetzung 

• Temperatur usw. 

→ dies sind sozusagen Einflußparameter der Kurven im Bild F 3.96 

→ hier wichtigste Kurve: σc = f(σ1) 

Druckfestigkeitskennlinien bzw. Verfestigungsfunktion 

→ typische Materialeigenschaftsfunktion – hier Geraden, s. Bild F 3.81 - 

für die Verfestigung eines Schüttgutes infolge einer Verfestigungsspan- 

nung σ1, siehe Folie F 3.97 

→ Damit korrespondiert physikalisch begründet eine analoge lineare Funk- 

tion der Verfestigung von Partikelkontakten, siehe F 3.98 

→ typische Kurvenverläufe für ein klassifizierbares Schüttgutverhalten → 

vergleiche auch mit ffc-Werten (siehe F 3.80), siehe Folie F 3.99 

a) trocken kohäsionslos σc = 0 ⇒ trockener, rieselfähiger Sand 

b) trockene, mineralische Pulver, feinkörnig, ⇒ oft Geraden 

c) feuchte, kohäsive, inkompressible (d.h. meist mineralische) Schüttgü- 

ter, verhältnismäßig grob, ⇒ meist flache Kurven (z. B. Glassand) 

d) feuchte, kohäsive, feine (gering kompressible) Schüttgüter bzw. Pulver 

⇒ meist Geraden, z. B. Filterkuchen, Abfälle 

e) feuchte, kohäsive, sehr kompressible Güter, 

⇒ d.h. mit viel innerer Porosität, z. B. Rohbraunkohle (Verhalten wie 

ein "Schwamm" oder "Ton") 

f) trockene fasrige Güter, erst σc = 0, dann steiler Anstieg, 

⇒ formschlüssige Bindungen, "Verhakungen", "Verfilzung" 

⇒ vergleiche mit e) ohne Feuchte, z.B. Abfallstoffe, Holzspäne u.ä. 

g) hohe Zeitverfestigungen durch Festkörperbrücken, Übergang zum 

Festkörperverhalten 

• Kristallisation, Anfrierungen 

• chemische Reaktionen 

• Erstarren hochviskoser Inhaltsstoffe mit Bindemittelwirkung 

• Sinterbrücken 

3.4.2 Übersicht des mechanischen Verhaltens kohäsiver Pulver 



54

• Nachgiebiges und Steifes Partikelkontakt- u. Pulververhalten, s. F 3.100 

→ Physikalisch begründete Charakterisierung der mechanischen Eigen- 

schaften, feinkörniger, kohäsiver und kompressibler Pulver! 

Aber auch: 

3.4.3 Tabelle mit „Datenblatt Schüttgutkennwerte“ 

• Übersicht wesentlicher Eigenschaftskenngrößen von Feststoffpartikeln 

hinsichtlich Lager- und Förderverhaltens, F 3.101 

• oft nur verbal klassifizierbar, z.B. mit Zwischenwerten: 

Tabelle 3.3: Schüttgutklassifizierung und Bewertung 

laufende Nummer 1 2 3 4 5 6 

obere Klassengrenze 0 0,5 1 1,5 2 2,5 

verbale Bewertung nicht sehr gering gering mittel stark sehr stark 

• Zusammenstellung der 14 Eigenschaftsgruppen (hier ≈ 100 Kennwerte) 

sowohl nach praktischen als auch nach wissenschaftlichen Gesichtspunkten 

sinnvoll 

• noch nicht vollständig, zukünftig erweiterbar ! 

Übungsbeispiel 

• feines Kalzitpulver, SF 2, 3, 4, 5 

• Vergleich mit jeweiligen Werten der Studenten 

• σ0 = 0,5 kPa 

• ϕst = 44° 

• σc- Gerade, (ff-Werte, s. 4.) 

• ϕi meist degressiv oder schwach steigend 

→ Fließorte werden mit zunehmendem Druck steiler, Reibung steigt 

mit zunehmender Abplattung der Partikelkontakte bei trockenen 

Gütern 

→ bei feuchten Gütern sinkt manchmal ϕi mit steigendem Druck, d.h. 

Auspressen von Wasser aus der inneren Porosität bildet sog. "Gleitfilme" 

• ϕe → abfallend, physikalisch begründet! siehe F 3.81 und Gl.( 3.99), 

• ρb meist Potenzansatz nach Gl.( 3.121) oder ( 3.128). 



55

3.5 Durchströmungs-, Fluidisier- und Entlüftungsverhalten 

3.5.1 Durchströmungsverhalten von Partikelschichten 

Die Strömung eines Fluids durch eine Partikelschicht spielt bei vielen Pro- 

zessen eine wichtige Rolle. Beispiele dafür sind: 

- Wirbelschichtprozesse, 

- die mechanische Flüssigkeitsabtrennung durch Filtrieren, 

- Trennungen mittels Hochdruck-Flüssigchromatographie (HPLC), 

- die Sedimentation im Bereich der Zonensedimentation, 

- das pneumatische Mischen, Homogenisieren, 

- die pneumatische Förderung und 

- Reaktionen in Festbettreaktoren, Schacht-, Hoch- und Drehrohröfen. 

Dabei sind die Partikelschichten sowohl hinsichtlich ihrer Auflockerung als 

auch ihres Bewegungszustandes voneinander abzugrenzen. 

Man spricht von einer ruhenden Schüttschicht (Festbett), wenn die einzelnen 

Partikeln mehr oder weniger in Form einer Zufallsanordnung aufeinanderliegen 

und die Schicht sich nicht bewegt. Die äußere Porosität ε einer 

solchen Schicht hängt vor allem von 

� der Anordnung der Partikeln zueinander in der Packung, 

� dem Mischungszustand, 

� den Partikelkontaktdeformationen, 

� den Wechselwirkungskräften zwischen den Partikeln sowie auch von 

� der Partikelgrößen- und Partikelformverteilung ab. 

Sie liegt bei vielen Schüttgütern um den Wert ε = 0,4 ... 0,5 MVT_e_1.doc - 

Schüttgutporositäten. 

In einer bewegten Schüttschicht befinden sich die Partikeln im wesentlichen 

noch im Kontakt, aber die Schicht bewegt sich als Ganzes durch den 

Prozeßraum. Derartige Verhältnisse liegen z.B. in Schacht- und Hochöfen 

vor. 

Läßt man durch eine auf einem fluiddurchlässigen Boden lagernde 

Partikelschicht ein Gas oder eine Flüssigkeit aufströmen, so wird die Schicht 

beim Überschreiten einer unteren Grenzgeschwindigkeit fluidisiert (Lockerungspunkt), 

d.h. die Partikeln werden durch den Fluidstrom in Schwebe 

gehalten (∆p Druckverlust der Partikelschicht, FG,B Bett- oder Schichtgewicht, 

siehe auch Gl.( 3.195)): 

∆p 

F 

G 

, B 

/ A 

≈ 

ρ 

b 

∆p 

⋅ g ⋅ h 

b 

≈ 1 



( 3.154) 

sie werden infolge Zunahme der Partikelabstände - damit der Porosität, siehe 

Abschnitt 1.3 MVT_e_1.doc - a_phis - relativ zueinander beweglich und 

führen insbesondere in Gas-Feststoffsystemen zunehmend durchmischende 

56

Bewegungen aus. Derartige Partikelschichten werden als Wirbelschichten 

(fluidized bed, Fließbett) bezeichnet. Der Schichtcharakter ist im Wirbel- 

schichtbereich noch gewährleistet. Die Porosität der Wirbelschichten körniger 

Stoffe umfaßt theoretisch den Bereich zwischen der Porosität am Lockerungspunkt 

εL und ε = 1, d.h. der Partikelschwebegeschwindigkeit. Übersteigt 

schließlich die Aufstromgeschwindigkeit die Schwebegeschwindigkeit 

der Partikeln, so werden diese von der Strömung transportiert – siehe Anwendung 

beim pneumatischen Transport. 

Es ist dann eine instationäre Wirbelschicht (Förderzustand der pneumatische 

Fließförderung oder Dichtstromförderung) entstanden. Voraussetzung 

für eine kontinuierliche, störungsfreie Fließförderung ist eine homogene 

Wirbelschicht im Einspeiser. Kanal- oder Blasenbildung führen zu einem 

unstetigen Förderstrom. Für die Beschreibung der Dichtstromförderung sind 

Kenngrößen des Schüttgutverhaltens notwendig. Dafür werden häufig das 

Entlüftungs- oder Gashaltevermögen und die Gasdurchlässigkeit einer 

Schüttung verwendet. Beide sind miteinander gekoppelt. Eine hohe Gasdurchlässigkeit 

bedingt ein geringes Gashaltevermögen und umgekehrt. 

Ein weiterer für die Verfahrenstechnik charakteristischer Zustand, der in 

diesem Zusammenhang zu nennen ist, sind die Rieselschichten. Hierbei 

bewegen sich die Partikeln aufgelockert unter Schwerkrafteinfluß durch ein 

ruhendes oder mit geringer Geschwindigkeit entgegenströmendes Gas. 

Beim Durchströmen einer Partikelschicht ist ein Fluid einem Widerstand 

ausgesetzt, und somit tritt ein Druckverlust ∆p ein, Bild F 3.102. 

Am einfachsten läßt sich dieser bei laminarer Durchströmung von Pulverschichten 

beschreiben, hier Re < 10, DARCY, CARMAN und KOZENY 

pb 

k pb 

V� 

∆ ∆ 

= A ⋅ u = k b ⋅ A ⋅ = ⋅ A ⋅ 

( 3.155) 

h η h 

b 

wenn für die Permeabilität einer Partikelschüttung 

b 

k b = k / η 

( 3.156) 

und nach CARMAN und KOZENY (Faktor 180 ⇒ für monodisperse Kugeln) 

gilt: 

k 

b 

3 2 

ε ⋅ dST 

= ( 3.157) 

180 ⋅ η ⋅ 

( ) 2 

1− 

ε 

Diese CARMAN-KOZENY-Gleichung ( 3.157) läßt sich übrigens auch unter 

Mithilfe der Poren-EULER-Zahl Euε als laminarer Spezialfall der 

ERGUN-Gleichung Gl.( 3.190) aufschreiben: 

( 1− 

ε) 

3 

∆p 

dST 

ε 

Eu ε = ⋅ ⋅ = ( 180 ... 150) 

⋅ 

( 3.158) 

2 

ρ ⋅ u h 1− 

ε 

Re 

f 

b 



57

Da der Strömungsraum ein vielgestaltiges Porensystem darstellt, dessen 

innere Geometrie – svw. Porengrößen- und Porenformverteilung - durch 

- die Partikelgrößen- und 

- Partikelformverteilung sowie 

- den Packungszustand (Porosität, Art der Packung) 

bestimmt ist, handelt es sich um ein sehr kompliziert zu beschreibendes 

Strömungsphänomen. Für dessen Modellierung sind erhebliche Vereinfachungen 

unerläßlich, siehe Tabellen F 3.103, a, b, c. Die dafür existierenden 

Modelle lassen sich vom physikalischen Grundansatz in zwei Hauptgruppen 

gliedern: 

1. Entweder man geht davon aus, daß es sich um eine Strömung durch ein 

Kontinuum („festes Dispersionsmittel“) mit inneren Kanälen („disperse 

Phase“) handelt, für deren Gestalt entsprechende Annahmen zu treffen 

sind (im einfachsten Fall parallele zylindrische Kanäle Gl.( 3.177)), oder 

2. man geht so vor, daß sich der Gesamtwiderstand einer Partikelschicht als 

Summe der Einzelkorn-Umströmungswiderstände darstellen läßt. 

Um wesentliche Zusammenhänge zu verdeutlichen, soll im folgenden ein 

kontinuumsmechanischer Modellansatz vorgestellt werden, der zur ersten 

oben genannten Hauptgruppe der Porendurchströmung zu zählen ist. Die 

Partikelschicht soll eine vollständige Zufallspackung darstellen, deren Querschnitt 

sich über die durchströmte Länge L oder Höhe ∆hb nicht ändert. Das 

Fluid wird unter den vorliegenden Druckabfällen als inkompressibel und 

weiterhin mit NEWTONschen Fließeigenschaften vorausgesetzt. Im Bild F 

3.102 ist das zugrundegelegte Modell dargestellt. Bezüglich des Anströmprofils 

und somit auch der Strömungsverhältnisse im Inneren können vor 

allem bei gröberen Körnungen in Randnähe Geschwindigkeitsmaxima auftreten 

(sog. Randgängigkeit), die eine Folge dort vorhandener größerer 

Porositäten ε → 1 und Porengrößen sind. 

Für den Druckverlust bei der Durchströmung eines Rohres gilt 

2 

FW 

U Rohr⋅ 

L ρf 

⋅u 

∆ pRohr 

= = λ Rohr⋅ 

⋅ 

( 3.159) 

A 4⋅ 

A 2 

Rohr 

Rohr 

D = 2⋅R Rohrdurchmesser 

L Rohrlänge 

= u / 2 mittlere Geschwindigkeit, wenn umax Maximalge- 

u max 

schwindigkeit im quadratischem Strömungsprofil: 

2 ⎛ r ⎞ 

u r = u( 

r) 

= u max⋅ 

⎜ 

⎜1− 

⎟ 

( 3.160) 

2 

⎝ R ⎠ 

2 

L ρf 

⋅u 

∆ pRohr 

= λ Rohr⋅ 

⋅ 

( 3.161) 

D 2 



58

und mit dem Druckverlustbeiwert (= cW Widerstandsbeiwert) einer 

- laminare (reibungsbehafteten) Rohrströmung Re < 2320 (HAGEN- 

POISEUILLE): 

64 

λ Rohr = f (Re) = 

Re 

und ( 3.162) 

- turbulente Rohrströmung 

# hydraulisch glatt 2320 < Re < 10 5 , laminare Grenzschicht der Dicke δG 

(BLASIUS) 

0, 

3164 

λ Rohr = 

( 3.163) 

1/ 

4 

Re 

# hydraulisch glatt 10 5 < Re< 3⋅10 6 , turbulente Grenzschicht (PRANDTL) 

λ 

1 

Rohr 

= 2, 

0⋅ 

lg 

( Re⋅ 

λ ) − 0, 

8 

Rohr 

# Übergangangsgebiet rauh, dr ≈ δG (COLEBROOK) 

λ 

1 

Rohr 

⎛ d r 2, 

51 

= −2, 

0⋅ 

lg⎜ 

+ 

⎜ 

⎝ 

3, 

715⋅ 

D Re⋅ 

λ 


Rohr 

⎞ 

⎟ − 

⎟ 

⎠ 


0, 

8 

dr mittlere Rauhigkeitsabmessung der Rohrwand 

# vollkommen rauh, dr >> δG, ⎟ D ⎛ D ⎞ 

Re > 400⋅ 

⋅ lg ⎜ 

⎜3, 

715 ⋅ 

d r ⎝ d r ⎠ 

( 3.164) 

( 3.165) 

0, 

25 

λ Rohr = 

( 3.166) 

2 

⎛ 3, 

715⋅ 

D ⎞ 

⎜lg 

⎟ 

⎝ d r ⎠ 

Mit Gl.( 3.162) gilt für den Druckverlust der reibungsbehafteten Rohr- 

strömung nach HAGEN-POISEUILLE 

L 

∆ pRohr = 32⋅ 

⋅ η⋅ 

u 

( 3.167) 

2 

D 

Die radiale Schubspannungsverteilung ist in diesem Falle übrigens linear, 

d.h., in der Mittelachse r = 0 sind u = umax und τ = 0 sowie an der Rohrwand 

sind r = R = D/2, u = 0 und τ = τmax: 

du u max τ ( r) 

= −η 

⋅ = 8 ⋅ η⋅ 

⋅ r 

( 3.168) 

2 

dr D 

Für die laminare Durchströmung einer Schüttung wird die HAGEN- 

POISEUILLE-Gleichung ( 3.167) mit einer mittleren Porendurchströmungsgeschwindigkeit 

u ε = u / ε und einem charakteristischen Porendurchmesser 

dε ≡ dh ≡ mittlerer hydraulischer Durchmesser gebildet: 

59

∆ 

h b η ⋅ u 

b = 32 ⋅ ⋅ 

( 3.169) 

d ε 

p 2 

ε 

u ε mittlere Strömungsgeschwindigkeit in den Poren 

dε 

charakteristische Abmessung des durchströmten Porensystems 

Nicht so sehr die Porosität sondern die Größe der Poren (Kanäle) bestim- 

men demnach die Durchströmbarkeit. 

Allgemein soll nun für den Druckgradienten dp/dhb 

Druckabfall ∆p/hb einer Schüttung geschrieben werden: 

= ≈ = = f ε 

dh b h b L 



f 

60 

bzw. bezogenen 

dp ∆p 

∆p 

gradp ( u ε , d , ε, 

η, 

ρ ) 

( 3.170) 

Dazu ist zunächst zu bemerken, daß das Konzept des hydraulischen 

Druchmessers aus dem Bereich der Rohrdurchströmung entlehnt ist, weitgehende 

Voraussetzungen enthält, d.h. 

- gerade Kanäle, 

- Konstanz der Wandschubspannungen an jedem Punkt der Wandoberfläche, 

- Gleichgewicht zwischen Druckabfall und Wandschubspannung 

und schon deshalb eine sehr weitreichende Vereinfachung darstellt. Hierzu 

kommt noch, daß durch einen (gegebenenfalls auch anders definierten) mittleren 

Porendurchmesser und die Porosität ε die innere Geometrie des Porensystems 

in bezug auf das komplizierte Strömungsphänomen nicht ausreichend 

widergespiegelt wird, da eine Porengrößenverteilung vorliegt. Allerdings 

liegen zur Berücksichtigung dieser Problematik bisher nur erste, für 

begrenzte Bereiche zutreffende Modellansätze. 

Zwischen der mittleren Strömungsgeschwindigkeit u ε in den Poren und der 

Anströmgeschwindigkeit u der Partikelschicht (Leerrohrgeschwindigkeit) 

besteht der Zusammenhang 

u = u / ε , ( 3.171) 

ε 

da sowohl die Volumenstrombilanz 

u ε ⋅ A Lücke = u ⋅ A 

( 3.172) 

als auch für ideale Zufallspackungen die Gleichheit von Flächen- und Volumenporosität 

gelten: 

ε = / V = A / A 

( 3.173) 

VLücke Lücke 

Der hydraulische Durchmesser dh der idealisierten Strömungskanäle der 

Schüttung läßt sich wie folgt definieren (s. MVT_e_1.doc - 

hydraulischerDurchmesser): 

d 

4⋅ 

A 

4πd 

4⋅ 

A 

4⋅ 

V 

h = durchströmt 

= 

Ubenetzt 

2 

4πd 

≡ durchströmt 

U benetzt⋅ 

l 

= f 

AS 

( 3.174) 

⋅ l

und unter Berücksichtigung des Hohlraumvolumens bei gegebener Porosität 

Vε = Vf 

= A ⋅ l = ε⋅ 

Vges 

= ε⋅ 

( VP 

+ V ) 

Vf ⋅ ( 1− 

ε) 

= ε⋅ 

VP 

Vf f 

ε 

f = V ⋅ 

( 3.175) 

1−ε 

V P 

und Oberfläche AS = U⋅l der Kapillaren der Länge l folgt eine einfache Proportionalität 

zwischen dem hydraulischen Durchmesser dh und dem SAU- 

TER-Durchmesser dST einer Körnung: 

d 

4 ⋅ ε ⋅ V 

4 ⋅ ε 

P 

h = = 

( 3.176) 

( 1−ε) 

⋅ AS 

( 1−ε) 

⋅ AS, 

V 

und da d ST= 

6 / AS, 

V ist auch der Zusammenhang zwischen einer Partikelgrößen- 

und Porengrößenverteilung herstellbar dh ≡ dε. 

2 ⋅ ε ⋅ dST 

dh 

= dε 

= 

( 3.177) 

3⋅ 

( 1−ε) 

so läßt sich für Gl.( 3.170) schreiben: 

∆p 

= f 

h 

b 

( u, 

d , ε, 

η, 

ρ ) 

ST 

f 



( 3.178) 

Wenn man von den bei der Partikelumströmung kurz erörterten Sachverhalten 

ausgeht (s. Abschn. 4.1.1 MVT_e_4.doc - Widerstandsbeiwert_kaskas), 

so darf angenommen werden, daß sich allgemein der Strömungswiderstand 

aus zwei Anteilen zusammensetzt: 

a) einem Zähigkeitsanteil (∆p ∼ η⋅u), der sich auch mit Hilfe des Durchströmungsgesetzes 

von Darcy (ggf. mit -Zeichen für Abnahme, Bild F 

3.102) 

∆p 

= = k ⋅ η⋅ 

u 

( 3.179) 

h 

gradp Darcy 

b 

k Darcy = 1/ 

k Durchflußwiderstand, reziproke Permeabilität siehe 

auch Gl.( 3.156) 

oder in einer verfahrenstechnisch üblichen Schreibweise ⇒ Stoffluß = 

Durchgangskoeffizient⋅Durchgangsquerschnitt⋅treibendes Potential (oder 

= Triebkraft) 

V 

u k b gradp 

A 

⋅ = 

� 

≡ ( 3.180) 

kb Permeabilität 

beschreiben läßt, und 

b) einem Trägheitsanteil (∆p ∼ ρf ⋅u 2 ) infolge des Staudruckes der Strömung 

(kinetische Energie), oder in einer verfahrenstechnisch üblichen 

Schreibweise mit der EULER-Zahl (= Druckkraft/Trägheitskraft): 

61

∆p 

= 2 

ρ ⋅ u 

= f ( h b, 

u, 

dST 

, ε, 

η, 

ρ ) 

62 

( 3.181) 

Eu f 

f 

Im Vergleich zur Partikelumströmung werden wegen der häufigen und 

starken Umlenkungen des Fluidstromes im Inneren einer Partikelschicht 

Trägheitswirkungen schon weit vor dem Einsetzen der eigentlichen Turbulenz 

dominieren. 

Aus dem Vorstehenden folgt der Ansatz /3.40./: 

∆p 

= k 

h 

b 

* * 

lam 

⋅ η ⋅ u + k 

* * 

turb 

⋅ ρ 

f 

⋅ u 

Mit der EULER-Zahl nach Gl.( 3.181) ist auch: 

f 

f 

2 



( 3.182) 

∆p 

* * η 

* * 

Eu = = k 2 lam ⋅ ⋅ h b + k turb ⋅ h b 

( 3.183) 

ρ ⋅ u ρ ⋅ u 

Die Abhängigkeit von der letzten noch dimensionsbehafteten Größe dST läßt 

sich auch mit Hilfe einer einfachen Dimensionsanalyse gewinnen, wenn 

man die Grundeinheiten L Länge, M Masse und T Zeit einsetzt: 

3 2 

3 

⎡⎛ 

M ⋅ L ⎞ L ⋅ T ⎤ ⎡⎛ 

M ⋅ L ⋅ T ⎞ L ⋅ T ⋅ L⎤ 

1 1 

= ⎢⎜ 

⋅ + [ L] 

⋅ 

2 2 ⎟ ⋅ 2 

2 2 

T L M L 

⎥ = ⎢⎜ 

⎟ ⋅ 

T L M L 

⎥ 

( 3.184) 

⎣⎝ 

⋅ ⎠ ⋅ ⎦ ⎣⎝ 

⋅ ⎠ ⋅ ⎦ L L 

Eu 2 

∆p 

η ⋅ h 

Eu ⋅ 

* 

b * b 

= = k lam ⋅ + k 

2 

2 turb 

( 3.185) 

ρf 

⋅ u ρf 

⋅ u ⋅ dST 

dST 

Somit verbleibt noch die Quantifizierung der Abhängigkeit von ε, die Ge- 

genstand vieler Untersuchungen war, die vor allem eine Abhängigkeit von 

Re der Durchströmung ergaben (s. z.B. /3.36/ bis /3.44/). Aufgrund des 

komplexen Strömungsphänomens existiert auch dafür noch keine allgemein 

anerkannte Formulierung. Im Bereich überwiegender 

- Zähigkeitswirkung geht man vorwiegend davon aus, daß der Durchströmungswiderstand 

proportional (1-ε) 2 /ε 3 ist, 

- im Bereich vorherrschender Trägheitswirkung dagegen ∼ (1 - ε)/ε 3 . 

Somit folgt aus Gl.( 3.185): 

2 ( 1− 

ε) 

η ⋅ h ( 1− 

ε) 

Eu ⋅ 

b 

b 

= k lam ⋅ ⋅ + k 

3 

2 turb ⋅ 

( 3.186) 

3 

ε ρf 

⋅ u ⋅ dST 

ε dST 

Der erste Term dieser Gleichung ist offensichtlich bei vorwiegender Zähigkeitswirkung 

wesentlich, der zweite dagegen bei dominierenden Trägheitskräften. 

Gl.( 3.186) läßt sich nun durch Einführen einer modifizierten Poren- 

EULER-Zahl Euε(Re) ≡ cW(Re) - manchmal auch analog der Rohrdurchströmung 

Widerstandszahl λ(Re) genannt - wie folgt umstellen: 

∆p 

dST 

1− 

ε 

Eu ε = ⋅ ⋅ 

( 3.187) 

2 

3 

ρ ⋅ u h ε 

f 

b 

h 

h

wobei mit der REYNOLDS-Zahl 

Re f 

= u ⋅ dST 

⋅ ρ / η 

( 3.188) 

für Gl.( 3.186) gilt: 

( 1− 

ε) 

∆p 

d ε 

Eu + 

ε = 

ρf 

ST ⋅ 2 

⋅ u h b 

3 

⋅ = k lam ⋅ 

1− 

ε Re 

k turb 

( 3.189) 

Die Quantifizierung ergab für Brechgut mit enger Partikelgrößenverteilung 

nach ERGUN /3.40./: 

( 1− 

ε) 

3 

∆p 

dST 

ε 

Eu ε = ⋅ ⋅ = 150 ⋅ + 1, 

75 

2 

( 3.190) 

ρ ⋅ u h 1− 

ε Re 

f 

b 

Diese Form des Widerstandsgesetzes der Durchströmung wird verbreitet für 

gröberes Gut (etwa d > 1 mm) genutzt, obwohl dabei die der Ableitung 

zugrundeliegenden weitreichenden Vereinfachungen nicht übersehen wer- 

den dürfen, die die quantitativen Modellaussagen erheblich einschränken 

können. 

Für feinere Schüttgüter werden damit u.U. zu hohe Druckverluste berechnet. 

Deshalb findet sich in der Fachliteratur eine Reihe mehr oder weniger davon 

abweichender Formulierungen des Widerstandsgesetzes der Durchströmung, 

die vorwiegend für eingeschränkte Re-Bereiche gelten: F 3.103, a, b, c 

Da sich dreitermige Ausdrücke für die Erfassung des Einzelteilchen- 

Widerstandes im gesamten verfahrenstechnisch interessierenden Re-Bereich 

als sehr leistungsfähig erwiesen haben, s. auch Gl.( 3.213), so sind in neuerer 

Zeit auch entsprechende dreitermige Modellansätze für die Durchströmung 

bekannt geworden, die für ε → 1 in die Gleichungen der Umströmung 

von Einzelteilchen übergehen (s. z.B. /3.35.//3.37./), Tabelle Bild F 

3.103.c.10 

3.5.2 Durchströmung von Wirbelschichten 

Bei der Durchströmung einer feinkörnigen Schüttung, die auf einem fluiddurchlässigen 

Boden (Anströmboden) in einem schachtartig ausgebildeten 

Apparat lagert, setzen unmittelbar vor dem Übergang in den fluidisierten 

Zustand zunächst gewisse beschränkte Umordnungen ein, d.h. einzelne Partikeln 

verändern ihre Lage, andere können vibrieren oder bewegen sich innerhalb 

begrenzter Gebiete. Schließlich vollzieht sich mit weiterer Geschwindigkeitssteigerung 

der Übergang in das Gebiet, in dem die von der 

Strömung auf die Schicht ausgeübten Kräfte den statischen Druck der Schüttung 

auf das gesamte Volumen hinweg überwinden. Die Porosität ist dann 

so groß geworden, daß die einzelnen Partikeln gegenseitig vollständig beweglich 

werden, Wirbelschicht, Fließbett, Bild F 3.104. Dieser für den 



63

Übergang charakteristische Punkt wird als Lockerungspunkt (Wirbel- 

punkt) und die entsprechende Fluidgeschwindigkeit als Lockerungsge- 

schwindigkeit uL bezeichnet. Allerdings ergibt sich nur für enge Partikelk- 

lassen ein scharf definierter Lockerungspunkt, bei Vorliegen breiterer Parti- 

kelgrößenverteilungen ein Lockerungsbereich. 

Hier wird der Fließverhalten eines Schüttgutes mit bevorzugter 

COULOMB-Reibung zwischen den Partikelkontakten (Ausbildung eines 

sog. Schüttkegels) verlassen, siehe Abschnitt 3.2.2. Der Partikelgerüstdruck 

σ (effektive Normalspannung σ´) strebt durch den zunehmenden Poren- 

fluiddruck p ≡ ∆p, siehe Gln. ( 3.192) und ( 3.234), gegen Null (Aufheben 

der Partikelkontakte) und das Fließverhalten dieses Fließbettes kommt dem 

eines viskosen reibungsarmen Fluides nahe („Abfließen“ oder Schüttke- 

gelzusammenbruch). 

σ = σ − = σ − ∆p 

→ 0 

( 3.191) 

ges 

p ges 

σges gesamter übertragbarer Druck 

Mit einer Flüssigkeit als Fluid entsteht nach Überschreiten des Lockerungs- 

punktes immer eine entsprechend der Fluidgeschwindigkeit sich weiter aus- 

dehnende homogene Wirbelschicht, in der Gleichgewicht zwischen den auf 

sie wirkenden Strömungskräften und dem um den Auftrieb verminderten 

Gewicht der Schicht besteht, Bild F 3.104 /3.45.//3.46./. 

( F 

G, 

b 

∆p 

− F 

A 

) 

/ A 

≈ 1 



( 3.192) 

Dieser Zustand ist dadurch gekennzeichnet, daß die Partikel über das gesamte 

Schichtvolumen weitgehend statistisch homogen verteilt sind. 

Gas-Feststoff- Systeme verhalten sich im allgemeinen anders. Oberhalb des 

Lockerungspunktes treten gutabhängig in geringerem oder größerem Abstand 

von diesem Instabilitäten auf. So bilden sich meist sog. Blasen, d.h. 

mehr oder weniger feststoffarme Gebiete, die nach oben aufsteigen und sich 

durch Koaleszenz vergrößern. Die Mindest-Fluidgeschwindigkeit, bei der 

Blasenbildung eintritt, liegt für nicht bzw. schwach kohäsives Schüttgut 

(d.h. geringe Haftkräfte zwischen den Partikeln, sog. Gruppe B - Verhalten 

nach Geldart, Bild F 3.105) um so näher bei der Lockerungsgeschwindigkeit, 

je gröber die Partikel sind /3.47.//3.48/. 

Mit wachsender Fluidgeschwindigkeit wird die Durchbewegung in der Wirbelschicht 

immer heftiger. Allerdings expandiert diese im Vergleich zu 

Flüssigkeits-Feststoff-Systemen nicht viel über das Ausmaß hinaus, das bereits 

am Wirbelpunkt erreicht ist, Bild F 3.104. 

64

Im instabilen Übergangsbereich zur instationären Wirbelschicht können 

bei genügend schlanken und hohen Wirbelschichtapparaten und nicht fein- 

körnigem Gut Blasen auftreten, die sich über den gesamten Schichtquer- 

schnitt erstrecken, Bild F 3.105. Dann ergeben sich stoßartige Auf- und Ab- 

bewegungen (stoßende Wirbelschicht, slugging). 

Weitere Inhomogenitäten können dadurch bedingt sein, daß das eintretende 

Gas vom Anströmboden ungenügend verteilt wird, so daß dieses die Schicht 

nur in begrenzten Bereichen durchbricht (durchbrochene Wirbelschicht, 

channeling). Wirbelschichten, der zuletzt geschilderten Art werden als inhomogene 

Wirbelschichten bezeichnet. In ihnen ist der Feststoff ungleichmäßig 

verteilt, und die Porosität unterliegt starken örtlichen und zeitlichen 

Schwankungen. 

Besondere Schwierigkeiten hinsichtlich des Fluidisierens bereitet kohäsives 

bis sehr kohäsives, feinstkörniges Schüttgut (sog. Gruppe C der GEL- 

DART-Klassifizierung F 3.105. Auf Grund ihrer Feinheit ist der Durchströmungswiderstand 

sehr hoch bei sehr geringer Gasdurchströmungsgeschwindigkeit, 

siehe Gl.( 3.169). Infolge der hohen Partikelhaftkräfte ist die Strömungswiderstandskraft 

nicht in der Lage die einzelnen Partikelkontakte abzulösen. 

Es bleibt das schlecht durchströmbare Kontinuum weitstgehend 

erhalten und nach Gasdurchbruch bilden sich größere Strömungskanäle mit 

hoher Gasgeschwindigkeit. Das Gas „sucht“ sich folglich den Weg des geringsten 

Strömungswiderstandes, Bild F 3.105. 

Sämtliche bisher behandelten Wirbelschichtzustände kann man, wenn von 

den Instabilitäten abgesehen wird, als stationäre Wirbelschichten bezeichnen. 

Hierbei ist die obere Schichtbegrenzung gegenüber dem darüber befindlichen 

Fluidraum noch deutlich ausgeprägt. Allerdings werden dabei 

einzelne Partikeln schon nach oben herausgeschleudert und gegebenenfalls 

auch mit der Fluidströmung abgeführt. Ob letztere vom Fluidstrom abtransportiert 

werden oder nicht, hängt letztlich vom Verhältnis der Schwebegeschwindigkeit 

der einzelnen Partikeln zur Fluidgeschwindigkeit ab. Solange 

die erstere größer als die letztere ist, werden die ausgestoßenen Einzelkörner 

wieder zurückfallen. Bei breiterer Partikelgrößenverteilung kann 

dieser Umstand für Klassierprozesse ausgenutzt werden, wenn der abzutrennende 

Feinkornanteil gering ist (klassierende Wirbelschicht). 

Wird die Schwebegeschwindigkeit aller Partikeln überschritten, so verschwindet 

die obere Schichtgrenze und das gesamte Gut wandert stark aufgelockert 

mit dem Fluidstrom (instationäre Wirbelschicht). Führt man bei 

sehr hohen Apparategrößen den ausgetragenen Feststoff wieder über eine 

Bypass-Leitung in die Wirbelschicht zurück, so erhält man eine sog. zirkulierende 

Wirbelschicht. 



65

Für weitere Betrachtungen über die Bildung von Wirbelschichten eignen 

sich Diagramme, in denen der auf das Bettgewicht normierte Druckabfall als 

Funktion der Leerrohr-Fluidgeschwindigkeit dargestellt ist. Dies ist im Bild 

F 3.104 in Form der Abhängigkeit 

∆p 

⋅ A 

= f ( u) 

( 3.193) 

m ⋅ g 

s 

und gemäß Kretschmer zusätzlich mit der Wirbelschichtdichte 

ms 

ρ WS = 

A ⋅ h 

= f ( u) 

( 3.194) 

WS 

in einem linearen Diagramm geschehen – darüber hinaus ist auch noch eine 

Darstellung log ∆ p = f (log u) 

üblich. 

Beide Kennlinien des dimensionslosen Druckverlustes und der Wirbelschichtdichte 

enthalten charakteristische Punkte, die die Eigenschaften des 

Schüttgutes hinsichtlich erwünschter homogener Fluidisierung beschreiben: 

(1) Ruhende Schüttung mit der Schüttgutdichte ρb ≈ ρb,0. 

(2) Durchströmte Schüttung; Es erfolgt eine Umorientierung der Partikeln, 

wodurch sich die Schüttgutdichte auf ρb,max = ρWS,max erhöhen kann. 

(3) Lockerungspunkt mit der Leerrohrgeschwindigkeit uL und der Wirbelschichtdichte 

ρWS,L oder Porosität εL; Schwerkraft der Schüttung und 

Strömungswiderstand befinden sich im Gleichgewicht. 

(4) Punkt des freien Fließens mit der Leerrohrgeschwindigkeit u * ; Hier 

liegt ein optimales Fluidisierungverhalten hinsichtlich verminderter Blasen- 

und Kanalbildung vor. 

(5) Zwischen Pkt. (5) und Pkt. (6) bleiben Wirbelschichtdichte und Druckverlust 

konstant. Es beginnt die Entmischung der Wirbelschicht. 

Der Wert des dimensionslosen Druckverlustes ist ein orientierendes Maß 

des Fluidisierungsgrades einer Wirbelschicht. Er gibt etwa den Gewichtsanteil 

der an der Wirbelschicht beteiligten Schüttgutmasse wieder. 

Bei kohäsiven Pulvern kann der dimensionslose Druckverlust etwas größer 

als 1 sein (hier im Bild F 3.104 nicht eingezeichnet, siehe Gln.( 3.154) und ( 

3.192)), da die Haftkräfte FH zwischen den Partikeln und eine Wandreibungskraft 

FWR überwunden werden müssen: 

∆ = F − F + F + F / A = 1− 

ε ⋅ ρ − ρ ⋅ g ⋅ h + F + F / 

( ) ( ) ( ) ( ) A 

p G A WR H 

s f b WR H 

( 3.195) 

Unmittelbar im Anschluß zwischen (3) und (4) würde der dimensionslose 

Druckverlust auf den Wert von etwa 1 abfallen. Von jetzt ab befinden sich 

die von der Strömung auf die Partikelschicht ausgeübten Kräfte mit dem um 

den Auftrieb verminderten Gewicht im Gleichgewicht. Der Verlauf der 

Druckverlustkurve ist bei Verminderung der Fluidgeschwindigkeit durch 

eine Hysterese gekennzeichnet. Dies bedeutet, daß die Wirbelschicht in eine 



66

uhende Schüttschicht mit der Wirbelschichtdichte ρWS,L oder Porosität εL 

übergeht; für grobe Abschätzungen siehe auch Gl.( 3.200). 

Der Neigungswinkel β der Wirbelschichtdichte-Kurve charakterisiert die 

Intensität der Fluidisierung. Ein großer Winkel, also steiler Abfall der 

Dichte-Kurve sowie hohe Expansionszahl κE Gl.( 3.197), kennzeichnen eine 

hohe Fluidisierungsintensität und eine hohe Wirbelschichthomogenität (re- 

ziproke FROUDE-Zahl, svw. Haftkraftmerkmal). 

2 

1 ε ⋅ dε 

⋅ g 

Ho = = 

( 3.196) 

Fr u 

2 

L 

Ein kleiner Wert für β bedeutet eine geringe Wirbelschichthomogenität 

infolge Kanal- oder Blasenbildung. 

Eine quantitative Beurteilung des Fluidisierungs- und Förderverhaltens 

feinkörniger Schüttgüter ist mit den nachfolgend erläuterten Kennzahlen 

möglich, die aus den charakteristischen Leerrohrgeschwindigkeiten und 

Wirbelschichtdichten gebildet wurden. Die Expansionszahl κE kann als 

Druckverlustverhältnis interpretiert werden und ist 

2 

⎛ u L ⎞ 

κ E = ⎜ ≤ 1 * ⎟ 

( 3.197) 

⎝ u ⎠ 

u* Wirbelgasgeschwindigkeit beim „freien“ Fließen ohne nennenswerte 

Änderung der Wirbelschichtdichte Bild F 3.104 

Bei geringen Haftkräften ist uL ≈ u* und damit κE ≈ 1. Treten Haftkräfte auf, 

muß u* > uL sein und die Wirbelschicht expandiert κE < 1 durch Porositäts- 

zunahme mitels Ausbildung feiner Strömungskanäle. 

Vergrößern sich diese infolge Überwindung größerer Haftkräfte, kann ebenfalls 

κ ≈ 1 sein. Allerdings liegen hier vergleichsweise höhere Lockerungsgeschwindigkeiten 

uL (svw. Strukturmerkmal) vor. Aus diesem Grunde wird 

die Expansionszahl κE nach Gl.( 3.197) mit der Lockerungsgeschwindigkeit 

uL multipliziert. Um jedoch eine bessere Unterscheidungsmöglichkeit zu 

erhalten, wird in der Durchströmbarkeitszahl σD deren Quadrat verwendet: 

2 4 ∗2 

σ D = κE 

⋅ u L = u L / u 

( 3.198) 

Große σD bedeuten praktisch gute Durchströmbarkeit; kleine einen großen 

Druckanstieg bei der Festbettdurchströmung. σD spiegelt den spezifischen 

Energieeintrag (Dispergierwirkung) in ein Schüttgut wider. Eine leichte 

Durchströmbarkeit hat ihre Ursachen entweder in groben Partikeln oder in 

einer Kanalbildung auf Grund der wirkenden Haftkräfte. Je geringer die 

Leerrohrgeschwindigkeit am Lockerungspunkt uL ist, desto feiner hat sich 



67

Struktur der Durchströmungskanäle ausgebildet. Die Wirbelschichthomoge- 

nität wird besser und die Haftkräfte sind niedrig. 

Ein hohes Gashaltevermögen des Schüttgutes drückt sich ebenfalls in einer 

geringen Expansionszahl κE und leichte Durchströmbarkeit σD aus, siehe 

Abschnitt 3.5.3. 

Die Breite der Partikelgrößenverteilung des Wirbelgutes wird analog 

d95/d50 durch das Verhältnis des gewogenen Mittels der Masseverteilung 

(Index 3; das 3. Moment bewertet bevorzugt Grobes) zum SAUTER-Durchmessers 

dST = d-1,3 (bewertet bevorzugt Feines) berücksichtigt: 

d 

d 

1/ 

3 

d ⎛ o 

⎞ 

N 

1/ 

3 

⎜ 3 

d q ( d) 

d( 

d) 

⎟ ⎛ 3 ⎞ 

1/ 

3 

3 

d 

( M ) ⎜ ∫ ⋅ 

⎟ ⎜∑ 

m, 

i ⋅ µ 3, 

i ⎟ 

3, 

3 3, 

3 ⎝ du 

⎠ ⎝ i= 

1 

= = 

= 

⎠ 

−1 

−1 

1 

( M ) d 

N 

− 

ST 

o 

−1, 

3 ⎛ 

⎞ ⎛ 

1 

1 ⎞ 

⎜ − 

− 

d ⋅ q ( d) 

d( 

d) 

⎟ ⎜ d 

3 

m, 

i ⋅ µ 3, 

i ⎟ 

⎜ ∫ 

∑ 

⎟ ⎝ i= 

1 ⎠ 

du 

⎝ 

dm,i mittlerer Klassendurchmesser 

µ Masseanteil der i-ten Klasse 

3, 

i 

⎠ 



≥ 1 

( 3.199) 

i Partikelgrößenklasse 

Der Vergleich der Durchströmbarkeitszahl σD mit dem SAUTER-Durchmesser 

dST und dem Partikelgrößenverhältnis d3,3/dST liefert eindeutige Aussagen 

zwischen haftkraft- und partikelgrößenbedingter Durchströmbarkeit. 

1) Eine geringe Durchströmbarkeit σD bei geringem SAUTER-Durchmesser 

dST und großer Verteilungsbreite d3,3/dST bringt den Effekt der 

Einlagerung von feinen Partikeln in die Porenräume des Grobkorngerüstes 

zum Ausdruck. 

2) Eine geringe Durchströmbarkeit σD bei mittlerem SAUTER- 

Durchmesser dST und geringer Verteilungsbreite d3,3/dST zeigt relativ geringe 

Haftkräfte und die Ausbildung feiner Poren (Kanäle) an. 

3) Bei großer Durchströmbarkeit σD, großem SAUTER-Durchmesser dST 

und großer Verteilungsbreite d3,3/dST liegt immer ein grobes Schüttgut 

vor. 

Der mögliche Arbeitsbereich wird außerdem durch das Verhältnis der Wirbelschichtdichten 

ρWS/ρWS,max abgegrenzt. 

Der Punkt der maximalen Schüttgut- bzw. Wirbelschichtdichte (2) und der 

Punkt des freien Fließens (4) begrenzen den möglichen Arbeitsbereich einer 

pneumatischen Fließ- oder Dichtstromförderung, innerhalb dessen 

eine homogene Fluidisierung und Fließförderung möglich ist, siehe Bilder F 

3.104 und F 3.106 nach Kretschmer: 

1) ausreichende Feinheit der Partikeln: dST ≤ 60 µ m 

2) ausreichend breite Partikelgrößenverteilung: d3 , 3 dST 

> 3 

3) große Expansionszahl: 0, 18 E 1 ≤ κ ≤ 

68

4) kleine Durchströmbarkeitszahl: 

σ D 

2 2 

≤ 0, 

3 cm / s 

5) ausreichender Dichtebereich: ρ ρ ≥ 0, 

60 



WS 

WS, 

max 

Liegt die Leerrohrgeschwindigkeit am Pkt. (4) bei u* < 2 cm/s, dann ist das 

Schüttgut stetig förderbar, wobei der Förderrohrdurchmesser D > 10 mm 

sein muß. Bei 2 cm/s < u* < 3,5 cm/s muß D > 25 mm sein und für u* > 3,5 

cm/s müssen Homogenisierungshilfen eingesetzt werden. Eine Fließförderung 

ist nicht mehr möglich. Dann kann nur noch eine Pfropfenförderung 

realisiert werden. 

Die für den Übergang in den Wirbelschichtzustand kennzeichnende PorositätεL 

läßt sich für viele Systeme angenähert durch nachfolgende Beziehungen 

bestimmen /3.50/: 

1 1− 

ε L ≈14 

oder ≈ 11 

( 3.200) 

3 

2 3 

ψ ⋅ε 

ψ ⋅ε 

A 

L 

A 

L 

Der Übergang in den fluidisierten Zustand am Lockerungspunkt ist durch 

das folgende Kräftegleichgewicht bestimmt: 

( 1− 

ε ) 

Eu ⋅ ρ ⋅ u ⋅ h ⋅ 

∆ p = 

⋅ 

f 

2 

L L 

3 

dST 

⋅ εL 

L = 

h 

( FG 

− FA 

) / A = ( 1− 

εL 

) ⋅ ( ρs 

− ρf 

) ⋅ g L 

hL Schichthöhe am Wirbelpunkt ( 3.201) 

εL Porosität am Wirbelpunkt, F 3.104 

Daraus erhält man unter Berücksichtigung der ERGUN-Gl.( 3.190) für die 

Lockerungsgeschwindigkeit uL: 

1− 

ε 

= 42, 

9 ⋅ 

d 

η ⎡ 

⋅ ⋅ ⎢ 1+ 

3, 

1⋅10 

ρf 

⎣⎢ 

ε 

( ρ − ρ ) 

⋅ ρ 

η 

u L 

L 

ST 

3 

−4 

L ⋅ 

2 ( 1− 

εL 

) 

⋅ s f f 

2 

⋅ d 

3 

ST 

⋅ g ⎤ 

−1⎥ 

⎥⎦ 

( 3.202) 

oder für den Bereich, in dem die Zähigkeitskräfte für den Durchströmungs- 

widerstand überwiegen: 

( ρ − ρ ) 

3 

2 

1 εL 

s f ⋅ dST 

⋅ g 

u L = ⋅ ⋅ 

für ReL < 20 ( 3.203) 

150 1− 

ε η 

L 

oder für den Bereich, in dem die Trägheitskräfte vorherrschen: 

u 

1 

( ρ − ρ ) 

⋅ d 

⋅ g 

3 s f ST 

L = ⋅ εL 

⋅ 

für ReL > 1000 ( 3.204) 

1, 

75 ρf 

Theoretisch erstreckt sich der Wirbelschichtbereich von der Lockerungsge- 

schwindigkeit uL bis zur Schwebegeschwindigkeit der Einzelpartikeln, die 

dem Betrage nach mit der stationären Sinkgeschwindigkeit entweder im 

STOKES-Bereich der laminaren Partikelumströmung Re < 1 Gl.(4.44) 

MVT_e_4.doc - Sinkgeschwindigkeit_STOKES 

69

( ρ − ρ ) 

2 

s f ⋅ d ⋅ g 

u L ≈ vs 

= 

( 3.205) 

18 ⋅ η 

oder im NEWTON-Bereich 10 3 < Re < Rec = 2⋅10 5 der turbulenten Partikel- 

umströmung Gl.(4.45) MVT_e_4.doc - Sinkgeschwindigkeit_NEWTON 

u 

v 

3 

( ρ − ρ ) 

⋅ d ⋅ g 

s f 

L ≈ s = ⋅ 

( 3.206) 

ρf 

weitestgehend übereinstimmt. 

Das Ende der Druckverlustkurve der Schicht im Bild F 3.104 trifft theore- 

tisch auf die des leeren Rohres bzw. Schachtes ⇒ s. Druckverlust der Flug- 

förderung in pneumatischen Senkrecht-Fördereinrichtungen. 

Davon ausgehend soll nun das Durchströmungsproblem einer 

Partikelschüttung gemäß der 2. Modellvorstellung Abschnitt 3.5.1 als 

Umströmung aller Partikeln in einem Wirbel- oder Festbett behandelt 

werden (O. MOLERUS: Principles of Flow in Disperse Systems, Chapman 

& Hall 1993, p. 10). NP gleichgroße kugelförmige Partikeln haben daher 

einen Druckverlust ∆p, der sich aus des Widerstandskraft der Einzelpartikeln 

FW,P, siehe Gl.(4.10) MVT_e_4.doc - cW wie folgt zusammensetzt: 

∆ p ⋅ A = N ⋅ 

( 3.207) 

P FW 

, P 

Die Partikelanzahl im Festbett der Höhe hb ist mit dem Feststoffvolumenanteil 

(1-ε) 

V A ⋅ h b 

N P = ( 1− 

ε) 

⋅ = ( 1− 

ε) 

⋅ 

( 3.208) 

3 

V π / 6 ⋅ d 

P 

Es wird eine Festbett-EULER-Zahl EuB abweichend von Gl.( 3.187) als dimensionslose 

Druckverlust-Kennzahl mit dem 

Partikelumströmungswiderstand FW,P und der charakteristischen Porenströmungsgeschwindigkeit 

uε als Partikelanströmungsgeschwindigkeit nach Gl.( 

3.171) definiert: 

FW 

, P / A P 

cW 

≡ Eu B = 

( 3.209) 

2 

ρ / 2 ⋅ u 

f 

ε 

Mit den Gln.( 3.207) und ( 3.208) folgt 

( ) ( ) 2 

3 

2 ⋅ FW 

, P 

2 ⋅ ∆p 

⋅ π / 6 ⋅ d 

Eu B = 

= 2 

2 

A P ⋅ N P ⋅ ρf 

⋅ u ε π / 4 ⋅ d ⋅ 1− 

ε ⋅ h b ⋅ ρf 

⋅ u / ε 

2 

4 ∆p 

d ε 

Eu B = ⋅ ⋅ ⋅ 

( 3.210) 

2 

3 ρ ⋅ u h 1− 

ε 

f 

b 

Mit dem Druckverlust am Lockerungspunkt Gl.( 3.201) ergibt sich die 

EULER-Zahl für die Wirbelschicht, 



70

4 ρ − ρ d ⋅ g 

Eu ε 

s f 

2 

WS = ⋅ ⋅ ⋅ , ( 3.211) 

2 

3 ρf 

u 

wobei als charakteristische Partikelgröße d entsprechend den obigen Mo- 

dellannahmen der SAUTER-Durchmesser dST oberflächengleichwertiger 

Kugeln eingesetzt werden sollte. Man beachte die Plausibilität dieser Wirbelschicht-EULER-Zahl, 

d.h., der Grenzwert für ε→1 muß lim Eu WS = cW 

und auch 

4 

( 1− 

ε) 

⋅ h 

⋅ F 



2 ⋅ F 

ε →1 

lim Eu WS 

ε→1 

= ⋅ 

3 ρf 

2 

WS W, 

P 

W, 

P 

⋅ ⋅ = 

= 

2 

3 

2 

2 

⋅ u ⋅ π / 6 ⋅ d h WS 1− 

ε ρf 

⋅ u ⋅ π / 4 ⋅ d 

ergeben. Gl.( 3.211) umgestellt liefert die Anströmgeschwindigkeit u 

u 

4⋅ 

( ρ − ρ ) 

f 

⋅ ε ⋅d 

⋅ Eu 

WS 

d 

2 

= s f 

ST 

( 3.212) 

3⋅ 

ρ 

⋅g 

Für die allgemeine Durchströmungsbedingung Re < 10 4 wurde von MOLE- 

RUS (..., p. 27) für kugelförmige Partikel experimentell gefunden 

ε 

2 

1, 

5 

24 ⎪⎧ 

⎡d 

1 ⎛ d ⎞ ⎤⎪⎫ 

4 ⎪⎧ 

⎛ d ⎞ ⎪⎫ 

d 0, 

907 

Eu WS = ⋅ ⎨1 

+ 0, 

341⋅ 

⎢ + ⋅⎜ 

⎟ ⎥⎬ 

+ ⋅ ⎨1 

+ 0, 

07 ⋅⎜ 

⎟ ⎬ + 0, 

4 + ⋅ 0, 

1 

Re ⎪⎩ ⎢⎣ 

a 2 ⎝ a ⎠ ⎥⎦ 

⎪⎭ 

Re ⎪⎩ ⎝ a ⎠ ⎪⎭ 

a Re 

mit dem ( 3.213) 

⇒ 24 ⋅ { ... } Re 

ersten laminaren Widerstandsterm, 

⇒ 4 

Re 

Übergangsterm und dem 

⇒ 0,4 + ... Widerstandsterm für turbulente Durchströmung, 

die der Partikelumströmung, siehe Abschnitt Gl.(4.14) MVT_e_4.doc - Wi- 

derstandsbeiwert_kaskas, entsprechen. Der laminare Umströmungswider- 

stand von glatten Kugeln setzt sich übrigens aus 2/3 viskosem Reibungswi- 

derstand und 1/3 Druckwiderstand zusammen: 

2 

⎪⎧ 

⎡2 

d 1 ⎛ d ⎞ ⎤⎪⎫ 

Eu ⋅ Re = 24⋅ 

⎨1 

+ k exp, lam ⋅ ⎢ ⋅ + ⋅⎜ 

⎟ ⎥⎬ 

für Re

Mit einem einfachen Würfelzellenmodell erhält man entsprechend Abschnitt 

1.3 Gl.(1.102) MVT_e_1.doc - a_phis für das Partikelgrößen-Abstands- 

verhältnis im allgemeinen Fall: 

Zur Verdeutlichung soll folgendes einfaches Würfelzellenmodell dienen: 

l = d + 2 ⋅ a / 2 

Vs 

π ⋅ d 

ϕ s = = 

V 6 ⋅ l 

3 

3 

π ⋅ d 

= 

6 ⋅ 

3 

( ) 3 

d + a 

Mit einem relativen Partikelabstand ka analog einer KNUDSEN-Zahl 

k a = a / d 

( 3.215) 

und einer dem kubischen Packungsmodell monodisperser Kugeln entspre- 

chenden maximalen Packungsdichte ϕs,max = π/6 = 0,5326 erhält man 

ϕ 

( ) 3 

s, 

max 

ϕ s = 

bzw. ( 3.216) 

1+ k a 

ϕs, 

max 

= −1 

oder ( 3.217) 

ϕ 

k 3 

a 

d 

a 

= 

1 

k 

a 

s 

⎡ 

= ⎢ 

⎢⎣ 

3 

ϕ 

s, 

max 

ϕ 

s 

⎤ 

−1⎥ 

⎥⎦ 

−1 

= 

3 

3 

1− 

ε 

3 ( 1− 

ε) 

− 

max 

1− 

ε 

Für die Wirbelschichtdurchströmung hat MOLERUS 

( 1− 

ε) 

= 0, 

9 



( 3.218) 

3 ϕ 3 

s , max = 

max d.h. (1-ε)max = 0,729 ( 3.219) 

gewählt, so daß in Gl. ( 3.213) einzusetzen ist: 

⎛ d ⎞ 

⎜ ⎟ 

⎝ a ⎠ 

0, 

9 

= 

0, 

9 

3 

1− 

ε 

− 

3 

1− 

ε 

( 3.220) 

Diese Beziehung ( 3.213) läßt sich auch für den Druckverlust von mehr oder 

weniger gesättigten Suspensionen verwenden, wobei hier aber die REY- 

NOLDS-Zahl mit der Relativgeschwindigkeit zwischen Fluid und den Parti- 

keln gebildet wird: 

Re = u − v ⋅ d ⋅ρ 

/ η = u − v ⋅ d / ν 

( 3.221) 

Tr 

ST 

l 

l 

ST 

Außerdem sollen hier auch die Gleichungen für die Durchströmung eines 

Festbettes angegeben werden: 

2 

1, 

5 

24 ⎪ 

⎧ ⎡d 

1 d ⎪ 

⎫ 

⎛ ⎞ ⎤ 4 ⎪⎧ 

⎛ d ⎞ ⎪⎫ 

⎛ d ⎞ 0, 

891 

Eu B = ⋅ ⎨1 

+ 0, 

692⋅ 

⎢ + ⋅⎜ 

⎟ ⎥ ⎬ + ⋅⎨1 

+ 0, 

12⋅ 

⎜ ⎟ ⎬ + 0, 

4 + ⎜ ⎟ ⋅ 0, 

1 

Re ⎪⎩ 

⎢⎣ 

a 2 ⎝ a ⎠ ⎥⎦ 

Re ⎪⎩ ⎝ a ⎠ 

0, 

95 ⎪⎭ 

0, 

95 ⎪⎭ ⎝ a ⎠0, 

95 Re 

( 3.222) 

Die maximale Packungsdichte wird angenommen mit 

( 1− 

ε) 

= 0, 

95 

3 ϕ 3 

s , max = 

max d.h. (1-ε)max = 0,8574 ( 3.223) 

l 

72

Eu 

B 

⎛ d ⎞ 

⎜ ⎟ 

⎝ a ⎠ 

0, 

95 

= 

3 

0, 

95 

1− 

ε 

− 

3 

1− 

ε 



( 3.224) 

Für stärkere Abweichungen von der Kugelform erhöht sich der Widerstand: 

⎪ 

⎧ 

2 

24 

⎡d 

1 ⎛ d ⎞ ⎤ 

= ⋅ ⎨1 

+ 0, 

685⋅ 

⎢ + ⋅ 

2 

⎜ ⎟ ⎥ 

k ⋅ Re ⎪⎩ 

⎢⎣ 

a 2 ⎝ a ⎠ ⎥⎦ 

⎪ 

⎫ 

⎬ + 

⎪⎭ 

k 

4 ⎪⎧ 

⎛ d ⎞ 

⋅ ⎨1 

+ 0, 

289⋅ 

⎜ ⎟ 

⋅ Re ⎪⎩ ⎝ a ⎠ 

⎪⎫ 

⎬ + 

⎪⎭ 

73 

⎧ ⎛ d ⎞ 

⋅ ⎨0, 

4 + 0, 

514⋅ 

⎜ ⎟ 

⎩ ⎝ a ⎠ 

1, 

5 

ψ 

0, 

95 ψ 

0, 

95 ψ 

0, 

95 

kψ 

1, 

5 

1 

k 

( 3.225) 

Partikelformfaktor nach Gl.(4.47) MVT_e_4.doc - Formkorrektur 

Vor allem Wirbelschichten mit Gasen als Fluid werden wegen ihrer mannigfaltigen 

Vorteile heute in der Verfahrenstechnik verbreitet angewendet: 

- Bei mechanischen Prozessen nutzt man ihre intensive Mischwirkung 

und z.T. auch ihre Klassierwirkung aus, 

- bei thermischen Prozessen vor allem den intensiven Wärme- und Stoffübergang 

beim Wärmeübertragen, beim Trocknen, bei der Adsorption, 

- Schließlich haben sie umfangreiche Bedeutung für die Reaktionstechnik 

(katalytische Gas-Feststoff-Reaktionen) wobei die intensive Durchmischung 

gleichmäßige Temperaturen über das Volumen hinweg gewährleistet. 

- Der fluidisierte Zustand kann auch hinsichtlich der Prozeßsteuerung vorteilhaft 

sein (leichterer Feststofftransport durch den Prozeßraum, Förderung 

und Automatisierbarkeit). 

⎫ 

⎬ 

⎭

3.5.3 Entlüftungsverhalten 

Wird ein Schüttgut von Luft durchströmt, kann es beim Erreichen des Wir- 

belpunktes fluidisiert werden. Das Fließverhalten einer solchen Wirbel- 

schicht läßt sich nahezu wie das eines viskosen Fluids (NEWTONsche Flüssigkeit) 

beschreiben. Der umgekehrte Prozeß von einer Fluidisation zum 

Erreichen des Fließverhaltens einer Schüttung (COULOMB-Reibung) stellt 

die Entlüftung dar. 

Eine Ausnahme stellen dabei sehr kohäsive Schüttgüter dar, die sich hinsichtlich 

ihres Fluidisationsverhaltens in die Gruppe C der Einteilung nach 

Geldart /20/ F 3.105 einordnen würden, da diese Materialien extrem schwierig 

zu fluidisieren sind. In erster Linie bilden sich bei Schüttgütern der 

Gruppe C Kanäle, durch die die Luft entweicht, und eine Fluidisierung tritt 

nicht ein. 

In dem betrachteten Fall, daß ein Austraggerät aus einem Einfülltrichter in 

eine pneumatische Förderanlage dosieren soll, gibt es an zwei Stellen die 

Möglichkeiten, eine Fluidisierung des Schüttgutes zu erreichen. 

1. Eine Variante ist, daß Luft durch das Schüttgut im Austraggerät strömt 

und es versucht zu fluidisieren. Da aber die Ausdehnung des Materials 

Voraussetzung dafür ist, ist eine Fluidisierung des Materials in diesem 

Fall nicht denkbar. Durch die räumliche Begrenzung des Schüttgutes im 

Austraggerätekanal kann die Porosität durch die Luftdurchströmung nicht 

verändert werden. 

2. Die zweite Möglichkeit resultiert aus der pneumatischen Befüllung eines 

Vorratsbunkers. Von dort kann bei zu geringer Verweilzeit (z.B. Kernfluß, 

d.h. Kurzschlußströmung) fluidisiertes Material in den Einfülltrichter 

des Dosierers gelangen. 

3. Außerdem kann allein durch die Strömung beim Befüllen des Einfülltrichters 

aus dem Vorratsbunker das Material so mit Luft angereichert 

werden, daß es zu einer Fluidisierung kommt. 

Da auf Grund der fehlenden Wandreibung von fluidisiertem Material das 

Förderprinzip der Austraggeräte unwirksam ist, muß die minimale Verweilzeit 

im Trichter abgeschätzt werden können, die das Schüttgut zum Entlüften 

benötigt. Im Einfülltrichter muß durch richtige Wahl des minimalen 

Füllstandes gewährleistet sein, solange "altes", bereits entlüftetes Schüttgut 

ausgetragen wird, bis sich das darüber befindliche Material entlüftet hat. 

Die ersten umfangreichen Betrachtungen zum Entlüftungsverhalten wurden 

von Johanson und Jenike /21/ durchgeführt. Aus einer Gleichgewichtsbetrachtung 

an einer Schüttgutscheibe der Dicke dz ergibt sich aus der Kontinuitätsgleichung 

für die Gasströmung, daß die zeitliche Änderung der gespeicherten 

Luftmenge im Volumenelement genauso groß wie die Änderung 



74

des Massestromes der Luft durch das Volumenelement sein muß, vgl. Bild 

3.28: 

a) Kontinuitätsgleichung der Gasströmung 

Gasströmung aus dem Volumenelement 

� 

= m� 

+ dm� 

= ρ ⋅ A ⋅ u ⋅ d ρ ⋅ A ⋅ u 

Bild 3.27: Gasströmung durch das Volumenelement 

b) Kräftegleichgewicht 

Bild 3.28: Kräftebilanzierung an einer Schüttgutscheibe 

( dm ) 

∂ 

∂t 

� � − 

f = mf 

, 2 − mf 

, 1 = dmf 

� 



( 3.226) 

Setzt man die Größen ein, die im Bild 3.28 aufgeführt werden, ergibt sich: 

∂ 

∂ 

( ρ ⋅ ε ⋅ A ⋅ dz) 

∂t 

( ρ ⋅ A u) 

f = −d 

f ⋅ 

( ρ ⋅ ε) 

∂( 

ρ ) ∂( 

ε) 

∂( 

ρ ⋅ u) 

f 

∂t 

mf , 1 f , 2 f f 

f 

= ε 

f 

∂t 

+ ρ 

f 

⋅ 

∂t 

= − 

f 

∂z 

( 3.227) 

( 3.228) 

Setzt man nun die Gültigkeit des idealen Gasgesetzes bei einer konstanten 

Temperatur voraus, so sind der Porengasdruck p und die Dichte der Luft ρf 

einander proportional. Außerdem kann die Änderung der Porosität ∂ ε durch 

die Änderung der Schüttgutdichte beschrieben b ρ ∂ werden. Unter diesen 

Voraussetzungen ergibt sich: 

( u ⋅ p) 

∂p 

p ∂ρb 

d 

ε ⋅ − ⋅ + = 0 

( 3.229) 

∂t 

ρ ∂t 

dz 

b 

dm 

dm 

b 

f 

� 

= ρb 

⋅ A ⋅ dz 

= ρ ⋅ ε ⋅ A ⋅ dz 

mf , 2 f 

f 

= ρ 

( σ + d σ) 

+ ( p + dp) 

τ 

dmb / A = ρ b ⋅ g ⋅ dz 

τ 

σ + 

p 

⋅ A ⋅ u 

dz 

( ) 

z 

τ = tan ϕW 

⋅ λ ⋅ σ 

75

Die Gl.( 3.229) enthält drei voneinander abhängige Variablen p, ρ b und u 

die miteinander durch weitere Gleichungen verknüpft werden müssen. 

� Für laminare Durchströmung kann die Geschwindigkeit u, z.B. mit Gl.( 

3.155), durch den Druckverlust dp / dz beschrieben werden. 

� Weiterhin kann die Schüttgutdichte in Abhängigkeit von der Verfestigungsspannung 

dargestellt werden, z.B. Gl.( 3.133). 

Das Kräftegleichgewicht der betrachteten Schüttgutscheibe ergibt den Gesamtdruck 

als Summe aus Normalspannung des Schüttgutes (svw. Vertikaldruck) 

σ, Fluiddruck p, Reibungswiderstand der Partikelschicht an der 

Wand und Schüttgutgewicht, siehe Bild 3.28: 

µ W λ 

σ + dp − ⋅ σ ⋅ dz + ρ ⋅ g ⋅ dz = 0 

( 3.230) 

A / U 

d b 

Das Horizontaldruckverhältnis λ (Druckanisotropiekoeffizient), siehe Schüttec_4.doc 

- Horizontaldruckverh_Wandreib, wird in der Rechnung vereinfachend 

als konstant angenommen. 

Johanson und Jenike /21/ lösen die beiden Gleichungen mit Hilfe der Differenzen-Methode. 

Es ist unschwer zu erkennen, daß das einen relativ hohen 

Rechenaufwand erfordert, da für jede konkrete Anwendung die Differentialgleichungen 

erneut gelöst werden müssen. 

Aufgrund der aufwendigen Berechnung versuchen mehrere Autoren /22/, 

/23/, /24/ unter bestimmten Voraussetzungen einfachere Lösungen zu finden. 

Kirby /24/ entwickelte ein Modell der Porenluftdruckänderung, das die 

Entlüftung während des pneumatischen Befüllvorganges bei Vernachlässigung 

der Wandreibung beschreibt. 

∂ ∂ ⎡ ∂p 

⎤ d∆σ 

= C * + 

t z * ⎢ 

⋅ 

∂ ∂ ⎣ ∂z 

* ⎥ 

⎦ dt 

p ges 

Die Koordinate ist hier auf den reinen Feststoff bezogen: 



( 3.231) 

∂ z* = ( 1− 

ε) 

⋅ ∂z 

( 3.232) 

Er setzt konstante Permeabilität (konstante Durchströmungsbedingungen) 

und lineare Kompressibilität (siehe Gl.( 3.246)) voraus. Damit kann ein 

Verfestigungkoeffizient C* (siehe auch Gl.( 3.245)) aus der eckigen Klammer 

herausgezogen werden. 

2 ( 1− 

ε) 

CV 

C* = ⋅ 

( 3.233) 

d∆σges = d∆ (σ+p) ist ein Gesamtdruckinkrement mit den Anteilen 

Partikelgerüstdruck σ und Porengasdruck p während des Befüllens, wobei 

für den zeitlichen Zuwachs des Partikelgerüstdruckes σ auch gilt: 

∂σ 

∂σ 

= 

∂t 

∂t 

ges 

∂p 

− 

∂t 

( 3.234) 

76

Bild 3.29: Spannungsverteilung über die 

Tiefe 

Dieser wird in der Bodenmechanik gemäß 

TERZAGHI auch als effektive, d.h. wirk- p σ 

same (svw. tragende!), Spannung σ´ ≡ σ 

σges 

bezeichnet, da er den Scherwiderstand Z = 1 

durch Partikelhaftung und –reibung 

(COULOMB-Reibung) erzeugt. Während der Befüllung liegt das Schüttgut 

fluidisiert vor, d.h. der Porendruck p = σges entspricht dem Gesamtdruck 

und somit ist der Partikelgerüstdruck σ = 0. Durch Porengasströmung nimmt 

p ab und das Partikelgerüst beginnt zu tragen, d.h. σ steigt. Nach abgeschlossener 

Entgasung und Übergang in den Schüttgutzustand ist p ≈ 0 und 

somit wird σges ≈ σ. 

Die obige partielle Differentialgleichung ( 3.231) wird für normierte, feststoff-bezogene 

Größen, 

Höhe: Z = z * / H * mit ( 3.235) 

H* = ( 1− 

ε) 

⋅ H 

( 3.236) 

Zeit: 

Porengasdruck: 

* 2 

vs 

⋅ t 

T = ( 3.237) 

C * 

vs* = dz*/dt Befüllgeschwindigkeit ≈ const. 

p 

P = ( 3.238) 

ρ ⋅ g ⋅ H * 

s 

mittels Differenzenmethode für die Randbedingungen 

(1) einseitig, d.h. Oberteil durchlässig, undurchlässiger Boden, 

(2) beidseitig, d.h. Boden und Oberteil durchlässig 

numerisch gelöst /24/. 

Der Porenluftdruck am Ende der Befüllung ist dann geringer als bei isostatischen 

Verhältnissen. Die weitere Entlüftung muß dann nach /21/, /22/, /23/ 

oder /25/ mit dem verringerten Porenluftdruck als Startbedingung berechnet 

werden. 

Murfitt und Bransby /22/ vernachlässigen als Vereinfachung den Einfluß der 

Wandreibung und des Befüllvorganges sowie die Abnahme der Füllhöhe H 

während der Entlüftung (gilt für sehr schnelles Befüllen und geringe Abnahme 

der Füllhöhe H (geringe Setzung während der Entlüftung) und setzen 


0 


P = 1 

77

isostatische Verhältnisse voraus, pv = ρ b ⋅g⋅z. Die obige Differentialglei- 

chung ( 3.231) wird wie folgt vereinfacht angewandt: 

∂p 

= C 

∂t 

CV 

V 

2 

∂ p 

⋅ 2 

∂z 

Koeffizient der Verfestigung in m 2 /s, siehe Gl.( 3.245) 



( 3.239) 

Für eine anfänglich lineare Porendruckverteilung in die Tiefe z der 

Partikelschichten 

( z, 

t 0) 

= p ⋅ z / H 

p t 0 

pt=0 

= = und ( 3.240) 

Druckkonstante, Bezugswert des Porenluftdruckes 

( z 0, 

t) 

0 

p = = 

( 3.241) 

fanden Murfitt und Bransby /22/ als Lösung mit Hilfe der Fourierreihenentwicklung 

für einseitige Randdurchlässigkeit (1): 

⋅ ⎛ ⋅ π ⎞ ⎛ ⋅ π ⋅ ⎞ ⎛ ⎞ 

= ∑ ⋅ ⎜ ⎟ ⋅ ⎜ ⎟ ⋅ ⎜ 

⎜− 

⋅ ⎟ 

⋅ π ⎝ ⎠ ⎝ ⋅ ⎠ ⎝ ⎠ 

∞ 8 pt 

= 0 i i z 

2 t 

p sin sin exp i 

( 3.242) 

2 2 

i= 

1 i 

2 2 H 

t 37 

und für beidseitige Randpermeabilität (2) 

( ) ⎟ ⋅ 

⎛ ⋅ π ⋅ ⎞ ⎛ ⎞ 

= ∑ − ⋅ ⋅ π ⋅ ⎜ ⎟ ⋅ ⎜ 

⎜− 

⋅ 

⋅ π 

⎝ ⋅ ⎠ ⎝ ⎠ 

∞ 4 pt 

= 0 

i z 

2 t 

p cos i sin exp i 

( 3.243) 

i= 

1 i 

2 H 

t 37 

mit dem Kinetik- bzw. Zeitparameter t37 

t 

37 

2 

4 ⋅ H 

= 2 

( 3.244) 

π ⋅ C 

V 

und dem Koeffizienten der Verfestigung: 

C 

kb 

k 

b 

V = ( 3.245) 

k V + ε / ( pü 

+ p0 

) 

Permeabilität des Schüttgutes nach Darcy 

Da es immer wieder verschiedene Darstellungen des Gesetzes nach Darcy 

gibt, sei noch einmal auf die hier verwendete Schreibweise verwiesen: 

∆p 

u = k ⋅ 

( 3.155) 

b 

h b 

Der Zeitparameter t 37 ist dabei eine Bezugsgröße für beide e-Funktionen ( 

3.242) und ( 3.243), da in dem Fall i = 1 und t = t 37 der Exponent (- t / t 37 ) 

in den Gln.( 3.242) und ( 3.243) den Wert -1 annimmt. Das bedeutet, daß 

der Porenüberdruck pü wegen exp(-1) = 0,37 durch den Entlüftungsvorgang 

auf 37 % des Anfangswertes gefallen ist. 

In Gl.( 3.245) ist k V die Volumenkompressibilität des Schüttgutes, 

78

k V = dε / dσ ( 3.246) 

hier nur mit dem Partikelgerüstdruck σ (svw. wirksame Spannung) gebildet. 

σ = σges - (pü + p0) ( 3.247) 

pü Überdruck in den Poren gegenüber dem Normaldruck p0 

Oftmals bleibt der Gesamtdruck während der Entlüftung konstant. Es ändern 

sich nur seine jeweiligen Anteile Partikelgerüstdruck σ und Porengasdruck 

p, siehe 

Bild 3.29. Wird nun die Berechnung für den Porendruck am Boden des 

Bunkers (z = 0) entsprechend Gln. ( 3.242) und ( 3.243) nach i = 1 abgebro- 

chen, erhält man eine Abschätzung der Zeit t50, in der sich das Schüttgut um 

50 % abgesetzt hat und unter den genannten Bedingungen (geringe Änderung 

der Füllhöhe H und damit der Porosität ε) analog der Porenüberdruck 

auf die Hälfte verringert hat /25/: 

t = ln 2 ⋅ t 

( 3.248) 

50 

37 

Die hier angegebenen Gln.( 3.242), ( 3.243) und ( 3.248) gelten nur für den 

Fall, daß der Vertikaldruck im Bunker keine Veränderung mit der Zeit erfährt 

pv ≠ f(t). Diese Bedingung einer nur geringen Änderung des Vertikaldruckes 

ist bei Bunkern mit geringer Füllhöhe annähernd gegeben. Außerdem 

kann t50 nur ermittelt werden, wenn die Füllhöhe H und der Verfestigungskoeffizient 

CV als Konstanten behandelt werden, was wiederum 

nur bei geringen Füllhöhen und damit geringen Vertikaldrücken eingehalten 

werden kann. 

Zur praktischen Anwendung dieser Gleichung ( 3.244) muß in einem Laborversuch 

der Verfestigungskoeffizient CV ermittelt werden, indem in einem 

Zylinder eine Absetzkurve des fluidisierten Schüttgutes als Funktion der 

Zeit aufgenommen wird. Eine andere Möglichkeit besteht darin, in einer 

Wirbelschichtapparatur nach Abschalten der Luftzufuhr das Absetzverhalten 

in Abhängigkeit von der Zeit zu bestimmen. Aus dieser Kurve kann dann t50 

und daraus mit Gl.( 3.245) der Verfestigungskoeffizient CV ermittelt werden. 

Mit dem einmal ermittelten Wert CV für ein Schüttgut ist dann für jede 

Füllhöhe in einem Bunker die Zeit t50 oder mit Gl.( 3.244) jede andere Zeit 

berechenbar (mit den obengenannten Einschränkungen). 

In einem Beispiel wird als Schüttgut gemahlene Kreide (d50 = 65 µm, dST = 

45 µm, do = 3,18 mm) verwendet. Die berechnete Entlüftungszeit t50 = 14,6 

min für einen Bunker mit der Füllhöhe H = 2,74 m stimmt sehr gut mit dem 

experimentell ermittelten Wert von 15 min für diese Höhe überein (CV = 25 

cm²/s aus Laborversuch) /22/. 



79

Eine Nährungslösung, die unter ähnlichen Voraussetzungen wie die Glei- 

chungen von Murfitt und Bransby gilt, geben Tardos u.a. /23/ an ( i = 1 ): 

pü 

p 

( t, 

z) 

ü, 

max 

⎛ π ⋅ z ⎞ ⎛ t 

= cos⎜ 

⎟ ⋅ exp ⎜ 

⎜− 

⎝ 2 ⋅ H ⎠ ⎝ t 37 

⎞ 

⎟ 

⎠ 

Dabei wird für den Zeitparameter folgende Gleichung angegeben: 

t 

37 

0 

b 



( 3.249) 

2 

4 ⋅ H ⋅ ε 

= ( 3.250) 

2 

π ⋅ p ⋅ k 

Für die Gültigkeit müssen die folgenden Voraussetzungen gelten: 

� eine nahezu konstante Porosität ε ≈ konst., gilt für feine, kohäsive 

Schüttgüter mit geringer Permeabilität, 

� kein merklicher Wandeinfluß, d.h. p v ≈ ρ b ⋅g⋅z, 

� Permeabilität k b = konstant, 

� geringer Porenüberdruck pü

Für einen typischen Fall wird eine Beispielrechnung durchgeführt, wobei 

jetzt die Füllhöhe H als Variable in die Rechnung eingeht und als Bezugsfüllhöhe 

die Höhe nach Abschluß der Entlüftung Hc verwendet wird: 

- Bunkerabmessungen: D = 5 m; Hc = 10 m 

- Schüttguteigenschaften: d ST = 50 µm; ε0 = 0,6; ρ s = 2040 kg/m³; 

µW = 0,5; λ = 0,3 

Am Boden des Bunkers wurden die Zeiten t50 = 16,7 min und t10 = 58 min 

berechnet. Allerdings muß man sich den Entlüftungsvorgang bestehend aus 

zwei Teilprozessen, die sich überlagern, vorstellen. Das Absetzen des 

Schüttgutes (Verringerung der Porosität) erfolgt nur in einem relativ kurzen 

Zeitabschnitt am Anfang des Entlüftungsvorganges. Im Beispiel ist dieser 

Teilprozeß nach ca. 10 min abgeschlossen. Die weitere Entlüftung erfolgt 

dann analog zum Durchströmungsvorgang in Kornschichten bei konstanter 

Füllhöhe Hc . Zu diesem Zeitpunkt liegt das Schüttgut bereits nicht mehr 

fluidisiert vor! Dieses Ergebnis deutet darauf hin, daß die Zeit t50 als Verweilzeit 

in einem Bunker ausreichend ist, um der Gefahr, fluidisiertes 

Schüttgut zu fördern, vorzubeugen. 

Weiterhin wird eine umfassende Variation der einzelnen Einflußgrößen 

durchgeführt /25/. Dabei ergeben sich für die Zeit t50-Werte, die verallgemeinert 

werden können, da die Streubreite nicht zu groß ist: 

t 

50 

H 

/ 

2 

η⋅ 

Hc 

≈ 270 

für ( 3.252) 

d ⋅ p 

2 

ST 

0 

ρs 

⋅ g ⋅ Hc 

= > 0, 

75 

( 3.253) 

p 

0 

Für sehr geringe dimensionslose Füllhöhen H´ < 0,75 werden die Zeiten t 50 

länger und streuen stärker: 

t 

50 

2 

η⋅ 

Hc 

≈ ( 270... 

720) 

⋅ 

( 3.254) 

d ⋅ p 

2 

ST 

0 

Allgemein kann festgestellt werden, daß sich mit Abnahme der Wandreibung 

die Entlüftungszeit verlängert, da der Vertikaldruck im Material dann 

sehr groß wird (isostatischer Fall) und sich damit das Material stark verdichtet. 

Als Ergebnis der starken Verdichtung muß einerseits mehr Luft verdrängt 

werden, da das Porenvolumen sehr gering ist, und andererseits nimmt 

die Permeabilität mit steigender Verdichtung ab, so daß der Entlüftungsvorgang 

insgesamt durch beide Faktoren verlängert wird und t37 

steigt. 

Weiterhin nimmt die Entlüftungszeit zu, wenn es sich um ein stark kompressibles 

und gut fluidisierbares Schüttgut handelt oder die Porosität des 

Schüttgutes gering ist, ε0 ≈ ε(σ = 0) < 0,55. In beiden Fällen kommt es im 



81

Endzustand des Entlüftungsvorganges zu einer starken Verdichtung, so daß 

das im vorhergehenden Abschnitt Gesagte genauso zutrifft. 

Zum Abschluß dieses Kapitels sollen noch die verschiedenen Möglichkeiten, 

die Entlüftungszeit zu berechnen, für zwei ausgewählte Schüttgüter und 

drei Füllhöhen miteinander verglichen werden. Da die Einfülltrichter von 

Dosiergeräten nicht zu große Bauhöhen aufweisen, wurden die beiden Füllhöhen 

mit H = 1 m bzw. 2 m festgelegt. Die üblichen Nachfüllhöhen in einem 

Einfülltrichter bei Betrieb sind dagegen noch geringer, um die 

Dosierschwankungen zu minimieren. Es wurde deshalb zusätzlich die Entlüftungszeit 

für eine nachgefüllte Schüttschicht der Höhe H = 0,2 m berechnet. 

Bei diesen geringen Füllhöhen kann auch davon ausgegangen werden, 

daß die auftretenden Vertikaldrücke und damit die Abnahme der Füllhöhe 

nicht zu groß sein werden, so daß die Gültigkeit aller aufgeführten 

Gleichungen gegeben ist. 

Als Schüttgüter wurden die Flugasche (dST = 43 µm, ε = 0,65) und das 

Polypropylenpulver (dST = 193 µm, ε = 0,6) ausgewählt, da die Unterschiede 

zwischen diesen beiden Materialien in Hinsicht auf das Entlüftungsverhalten 

am größten sein dürften. Die Ergebnisse einer Beispielrechnung enthält 

Tab. 3.5. 

Tabelle 3.4: Übersicht über die mittleren Entlüftungszeiten (Verweilzeiten) 

Gl.( 3.248) /22/: 

Flugasche 

PP-Pulver 

Gl.( 3.251) /23/: 

Flugasche 

PP-Pulver 

Gl.( 3.254) /25/: 

Flugasche 

PP-Pulver 

dST in 

µm 

43 

193 

43 

193 

43 

193 

t50 in s 

H = 0,2m 

4,5 

0,3 

0,06 

0 

2,8 

0,1 

t50 in s 

H = 1 m 

112 

6,5 

1,4 (4,7) 

0,1 (0,4) 

70 

3,5 



t50 in s 

H = 2 m 

448 

24 

5,7 (19) 

0,4 (1,5) 

280 

14 

82 

Bemerkungen 

CV = 25 cm²/s 

CV = 460 cm²/s 

Klammerwerte für t10 kb = 1,28 . 10 -6 m ² /Pa⋅s 

kb = 1,54 . 10 -5 m ² /Pa⋅s 

H = Hc H ´ < 0,52 

H ´ < 0,18 

Für die Berechnung wurden folgende Annahmen getroffen: 

- Da der Koeffizient CV der Verfestigung, siehe Gl.( 3.245), nur für eine 

gemahlene Kreide (dST = 45 µm, C = 25 cm²/s) angegeben wird, muß 

eine Umrechnung in Abhängigkeit von der Korngröße erfolgen. 

Es gilt: CV ~ kb Ersetzt man nun kb durch die Permeabilität nach Carman und Kozeny 

siehe Gl.( 3.157), ergibt sich:

( ) 2 

3 2 

ε ⋅ dST 

k b = 

180 ⋅ η ⋅ 1− 

ε 

( 3.157) 

Daraus folgt: CV ~ d ² 

ST 

Da die verwendete Flugasche einen fast gleichen Sauterdurchmesser wie 

die Kreide besitzt, wurde CV = 25 cm²/s angenommen. Für das 

Polypropylenpulver ergab sich nach der Umrechnung auf dST = 193 µm 

der Wert CV = 460 cm²/s. 

- Die für die Gl.( 3.244) benötigten Werte kb wurden nach obiger Gleichung 

berechnet und sind in Tab. 3.4 angegeben. 

- Da für alle Werte H / ≤ 0,52, gilt Gl.( 3.254). Es wurde mit dem größten 

Wert gerechnet, so daß sich die längsten Zeiten t50 ergeben: 

2 

η ⋅ Hc 

t 50 ≈ 720 

( 3.254) 

2 

dST 

⋅ p0 

Außerdem wurde Hc = H angenommen, was bei geringen Füllhöhenänderungen 

keinen großen Fehler ergibt. 

Bei allen Gleichungen ergeben sich folgende Proportionalitäten: 

t 50 ∼ H² und t 50 ∼ 1 / d ST ² ( 3.255) 

Diese Abhängigkeiten gelten natürlich nur unter der Voraussetzung, daß 

sich die Schüttguteigenschaften (Porosität, Kompressibilität und Permeabilität) 

nicht ändern. Bei einer Maßstabsübertragung von einem Modellsilo auf 

ein Großsilo erscheint das fraglich. 

Die Modelle von Murfitt Gl.( 3.248) und Rathbone Gl.( 3.254) liefern ähnliche 

Ergebnisse, währenddessen Gl.( 3.251) um den Faktor 100 kürzere Zeiten 

ergibt. Eine mögliche Ursache kann darin bestehen, daß für die geringen 

Überdrücke (für den isostatischen Fall pü,max < 20 kPa) die angegebene 

Gleichung nicht mehr die volle Gültigkeit besitzt. 

Abschließend kann festgestellt werden, daß mit den Gln.( 3.248) und ( 

3.252) 

eine Berechnung der Zeit t50 erfolgen kann, die angibt, nach welcher 

Zeit der Überdruck in den Poren am Boden des Bunkers auf die Hälfte gesunken 

ist. Da der Entlüftungsvorgang aus zwei Teilprozessen besteht (siehe/25/), 

die sich überlagern, kann man davon ausgehen, daß das Absetzen 

des Schüttgutes (Verringerung der Porosität) nur in einem relativ kurzen 

Zeitabschnitt am Anfang des Entlüftungsvorganges erfolgt. Danach besteht 

nicht mehr die Gefahr, daß das Material fluidisiert vorliegt. Anhand der Beispielrechnung 

in /25/ ergab sich, daß sich zur Zeit t50 das Schüttgut bereits 

abgesetzt hat und sich nicht mehr im fluidisierten Zustand befindet, so daß 

diese Zeit als minimale Verweilzeit im Einfülltrichter eingehalten werden 



83

muß. Voraussetzung dafür ist, daß der Einfülltrichter als Massenflußtrichter 

ausgelegt wurde, da Pfropfenströmung notwendig ist. 

Literaturverzeichnis 

/1/ Gupte: Experimentelle Untersuchungen der Einflüsse von Porosität 

und Korngrößenverteilung im Widerstandsgesetz der Porenströmung 

Diss., Universität Karlsruhe, 1970 

/2/ Molerus, O.: Druckverlustgleichungen für die Durchströmung von 

Kugelschüttungen im laminaren und Übergangsbereich 

Chemie-Ingenieur-Technik 49 (1977) 8, S. 675 

/3/ Gatzky, D.: Modifizierte Schneckenförderer zum Dosieren und Entnehmen 

von Trockenfuttermitteln aus Behältern 

Agrartechnik 31 (1981) 8, S. 359-362 

/4/ Schuhmacher, W.: Zum Förderverhalten von Bunkerabzugsschnecken 

mit Vollblattwendeln, Diss., RWTH Aachen, 1987 

/5/ Bates, L.: Interfacing Hoppers with Screw Feeders, Proceedings: 

Reliable Flow of Paticulate Solids, Bergen (Norwegen), 1985 

/6/ Fritsch, D.: Zum Verhalten volumetrischer Schneckendosiergeräte 

für Schüttgüter, Diss., Universität Erlangen-Nürnberg, 1988 

/7/ Salzer, G.: Schüttgutförderer, Krausskopf-Verlag, 1968 

/8/ Goldacker, E.: Untersuchung zur inneren Reibung von Pulvern, insbesondere 

in Hinblick auf die Förderung in Extrudern, Diss., 

RWTH Aachen, 1971 

/9/ Autorenkollektiv: Verarbeitungstechnik (Lehrbuchreihe Verfahrenstechnik), 

Deutscher Verlag für Grundstoffindustrie, 1978 

/10/ Geisler, D.: Untersuchungen zum Schüttgutaustrag aus einem Bunker 

mittels Schneckenförderer Diss., TU Dresden, 1971 

/11/ Vetter, G.; Gericke, H.; Fritsch, D.: Zur kontinuierlichen Dosierung 

von Schüttgütern mit Schneckendosiergeräten 

Aufbereitungstechnik 25 (1984) 12, S. 705-717 

/12/ Colijn, H.; Caroll, P.J.: Design Criteria for Bin Feeders, Trans. 

Amer. Inst. Min.,Metallurg., Petrol. Engrs., 241 (1968), S. 389-404 

/13/ Tomas, J.: Untersuchungen zum Fließverhalten von feuchten und 

leichtlöslichen Schüttgütern, Freiberger Forschungshefte A 677, 

1983 

/14/ Kawakita, K.; Lüdde, K.H.: Some Considerations on Powder Compression 

Equations, Powder Technology 4 (1970), S. 61 

/15/ Motzkus, V.: Belastungen von Siloböden und Auslauftrichtern durch 

körnige Schüttgüter, Diss., TU Braunschweig, 1974 

/16/ Menges,G.; Hegele, R.; Langecker, G.: Theorie der Förderung im 

Einschneckenextruder, Plastverarbeiter, 23 (1972) 7, S. 455-460 

/17/ Schneider, K.: Der Fördervorgang in der Einzugszone eines Extruders, 

Diss., RWTH Aachen, 1968 

/18/ Fischer, P.: Auslegung von Einschneckenextrudern auf der Grundlage 

verfahrenstechnischer Kenndaten (Modelltheorie), Diss., 

RWTH Aachen, 1976 

/19/ Pontow, B.; Strecker, J.; Wiedemann, W.: Entwicklung eines Eintrag- 

und Dosiersystems für Kohlestaubdruckvergasungen 

BMFT-Forschungsbericht 82-203, 1982 

/20/ Geldart, D.: Types of Gas Fluidisation, Powder Technology, 7(1973), 

S. 285-292 



84

85 

/21/ Johanson, J.R.; Jenike, A.W.: Settlement of Powders in Vertical 

Channels Caused by Gas Escape, Journal of Applied Mechanics, 

39(1972)12, S. 863-868 

/22/ Murfitt, P.G.; Bransby, P.L.: Deaeration of Powders in Hoppers 

Powder Technology, 27(1980), S. 149-162 

/23/ Tardos, G.I. u.a.: Unsteady Flow of Compressible Gas through Consolidated 

Porous Media - Application to Deaeration of Hoppers 


/24/ Kirby, J.M.: Deaeration of Powders in Hoppers: a Simple Linear 

Theory including Filling, Powder Technology, 44(1985), S. 69-75 

/25/ Rathbone, T.; Nedderman, R.M.: The Deaeration of Fine Powders 



Prof. Dr. Jürgen Tomas, 16.04.2012

3.6 Feldgleichungen des ebenen Spannungszustandes 

Aus dem Bild 3.31 entnimmt man: 

σ = σ + σ ⋅ cos 2ψ 

σ = σ −σ 

⋅ cos 2ψ 

τ 

x 

y 

xy 

= σ 

M 

M 

R 

R 

R 

⋅ sin 2ψ 



( 3.256) 

und mit dem „Stoffgesetz“ des Fließortes mit Kohäsion: 

σ R = sin ϕi⋅ 

( σM 

+ σZ 

) 

( 3.61) 

σZ 

τ 

τc 

τxy < 0 

τxy 

ϕi 

ϕi 

Fließort 

σy 

σR 

σM 

2ψ 

Bild 3.31: Spannungszustand im beginnend fließenden Schüttgut 

eingesetzt folgt: 

σ = σ + σ ⋅ 1+ 

sin ϕ ⋅ cos 2ψ 

−σ 

σ 

τ 

x 

y 

xy 

= 

= 

( M Z ) ( i ) 

( σM 

+ σZ 

) ⋅ ( 1−sin 

ϕi⋅ 

cos 2ψ) 

( σ + σ ) ⋅ sin ϕ ⋅ sin 2ψ 

M 

Z 

eingesetzt in die Gln.( 3.21) 

i 

−σ 

Z 

Z 

+ σ 

+ σ 

Z 

σx 

Z 

−σ 

−σ 

und ( 3.22) mit den 3 Unbekannten σx, σy und τxy 

x − Richtung : 

∂σ ∂τ x xy 

+ = 0 

∂x 

∂y 

( 3.21) 

y − Richtung : 

∂σy 

∂τxy 

+ = ρb⋅g 

∂y 

∂x 

( 3.22) 

folgen aus diesen wiederum zwei gekoppelte partielle Differentialgleichungen, 

die sich hinsichtlich der beiden gesuchten Funktionen [ ] ( x, 

y) 

+ σ 

sowohl linear als auch nichtlinear bezüglich ψ( x, 

y) 

verhalten: 

∂( σ M + σ Z ) 

( + ϕ i ⋅ ψ) ⋅ 

( ) 

∂ 

∂( σ M + σ Z ) 

ϕ ⋅ ψ ⋅ 

( ) 

( ϕ ψ) ( + ) 

( + ) 

Z 

Z 

σ1 

σ 

M Z σ 

1 sin cos2 − 2 σ + σ ⋅ sin ϕ ⋅ sin 2ψ 

⋅ + 

∂ψ 

M Z i 

x ∂x 

sin sin 2 + 2 σ + σ ⋅ sin ϕ ⋅ cos2ψ 

⋅ = 0 

∂ 

∂ψ 

i 

M Z i 

y ∂y 

∂ σ σ 

1 − sin ⋅ cos2 ⋅ 

+ 2 ( σ + σ ) ⋅ sin ϕ ⋅ sin 2ψ 

⋅ + 

∂ 

∂ψ 

M Z 

i 

M Z i 

y ∂y 

∂ σ σ 

sin ϕ ⋅ sin 2ψ ⋅ 

+ 2 ( σ + σ ) ⋅ sin ϕ ⋅ cos2ψ 

⋅ = 

∂ 

∂ψ 

M Z 

i 

ρ 

x ∂x 

M Z i b 

⋅g 

( 3.257) 

86

Mittels Nutzung der Additionstheoreme für die Winkelfunktionen 

sin( α± 

β) 

= sin α⋅ 

cosβ 

± cos α⋅ 

sin β 

cos( α± 

β = cos α⋅ 

cosβ 

� sin α⋅ 

sin β 



( 3.258) 

und einer geeigneten Transformation mit einer dimensionslosen Spannung S 

S 

1 

2 tan ϕ 

M Z 

= ⋅ ln , ( 3.259) 

i 

σ 

σ 

M, 

0 

+ σ 

+ σ 

Z, 

0 

wobei für einen Rand, auf dem [ M + σZ 

] ( x, 

y) 

= σM, 

0+ 

σZ, 

0 

87 

σ ist, auch gilt ln(1) 

= 0 = S, lassen sich diese beiden Differentialgleichungen in eine für die Lö- 

sung günstige Form bringen (s. MOLERUS 1985): 

⎛ ϕi π⎞ 

exp( − 2 tan ϕi ⋅S) ⋅ sin⎜ψ 

+ − ⎟ 

⎛ ϕ π⎞ ∂(S + ψ) 

∂(S + ψ) 

⎝ ⎠ 

i 

2 4 ρb 

g 

tan⎜ 

ψ − + ⎟ ⋅ + = − 

⋅ 

⎝ 2 4⎠ 

∂x 

∂y 

⎛ ϕi π⎞ 

σ + σ 

2 sin ϕi ⋅ cos⎜ 

ψ − + ⎟ 

⎝ 2 4⎠ 

M, 0 Z, 

0 

⎛ ϕi π⎞ 

exp( − 2 tan ϕi ⋅S) ⋅ sin⎜ψ 

− + ⎟ 

⎛ ϕ π⎞ ∂(S − ψ) 

∂(S − ψ) 

⎝ ⎠ 

i 

2 4 ρb 

g 

tan⎜ 

ψ + − ⎟ ⋅ + = − 

⋅ 

⎝ 2 4⎠ 

∂x 

∂y 

⎛ ϕi π⎞ 

σ + σ 

2 sin ϕi 

⋅ ⎜ψ 

+ − ⎟ 

⎝ 2 4⎠ 

Diese ist vom Typ 

M, 0 Z, 

0 

cos 

( 3.260) 

∂u 

∂u 

a ⋅ + b ⋅ = c 

( 3.261) 

∂x 

∂y 

mit a(x, y, u), b(x, y, u) sowie c(x, y, u) und läßt sich mit Hilfe der 

Charakteristikenmethode lösen, siehe JENIKE (1961) und MOLERUS 

S.111 (1985). 

In Zylinderkoordinaten lauten die Gleichungen für das ebene Spannungsfeld, 

siehe auch vereinfacht ( 3.262): 

∂σr 

1 ∂τrθ 

σr 

−σθ 

r − Richtung : + ⋅ + + ρb⋅g 

⋅ cos θ = 0 

∂r 

r ∂θ r 

∂τrθ 

1 ∂σθ 

τrθ 

θ − Richtung : + ⋅ + 2 ⋅ − ρb⋅g 

⋅ sin θ = 0 

∂r 

r ∂θ r 

( 3.262) 

• Die z-Richtung aus der Zeichenebene heraus = Schlitzlängenkoordinate 

wird hier nicht betrachtet. 

• Der differentielle Spannungszuwachs lautet z.B. in x-Richtung: 

dx 

x ⋅ 

∂σ 

∆ σ = 

( 3.263) 

∂ 

• Dabei ist dr ⋅ sin dθ 

≈ dr⋅ 

dθ 

für kleine θ. 

• Die Terme dr⋅ dθ 

≈ 0 werden vernachlässigt.

Zusätzlich lassen sich auch die Gleichungen für das axialsymmetrische 

Spannungsfeld in Kugelkoordinaten aufschreiben. Dabei muß neben dem 

vertikalen Drehwinkel θ auch noch der Drehwinkel β in horizontaler Ebene 

berücksichtigt werden, siehe MOLERUS S.121 (1985). 

Für beide Spannungsfelder läßt sich deshalb gemeinsam formulieren: 

∂σr 

1 ∂τrθ 

1 

r − Richtung : ´ + ⋅ + ⋅ 

∂r 

r ∂θ r 

∂τrθ 

1 ∂σθ 

1 

θ − Richtung : + ⋅ + ⋅ 

∂r 

r ∂θ r 

[ σ − σ + m ⋅ ( σ − σ ) ] 

r 



r 

+ ρ ⋅g 

⋅ cos θ = 0 

88 

[ m⋅ 

( σ − σ ) ⋅ cot θ + ( m + 2) 

⋅ τ ] − ρ ⋅g⋅ 

sin θ = 0 

θ 

θ 

β 

β 

b 

rθ 

b 

( 3.264) 

wobei für die geometrischen Formfaktoren des Spannungsfeldes bzw. des 

Trichters zu schreiben ist: 

m = 0 ebenes Spannungsfeld und 

m = 1 axialsymmetrisches Spannungsfeld. 

σθ + ∆σθ 

τθ + ∆τθ 

r sindθ ≈ r dθ 

ρb g 

τθ 

dr σθ 

r 

(r + dr) dθ 

σr + ∆σr 

dθ 

τrθ + ∆τrθ 

θ 

σr 

τ 

rθ 

Bild 3.32: Ebener Spannungszustand im fließenden Schüttgut in Zylinderkoordinaten 

τrθ 

τrθ dθ 

∂τ rθ 

+ ⋅ 

dθ 

∂θ 

dθ 

σ 

σθ 

θ 

∂σ θ 

+ ⋅ d θ 

∂θ 

τrθ 

σθ dθ 

dθ

Partikel- und Schüttgutmechanik - Lehrstuhl Mechanische ...

Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.

Template löschen?

Als Template speichern?