Abitur 2014; Aufgabe B 2.1

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Abitur 2014, Aufgabe B 2.1
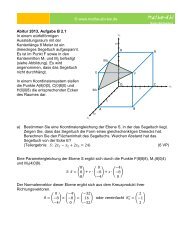
An einer rechteckigen Platte mit den Eckpunkten A(10|6|0), B(0|6|0), C(0|0|3) und
D(10|0|3) ist im Punkt F(5|6|0) ein 2m langer Stab befestigt, der in positive x 3 -Richtung
zeigt. Eine punktförmige Lichtquelle befindet sich zunächst im Punkt L(8|10|2).
(Koordinatenangaben in m).
a) Bestimmen Sie eine Koordinatengleichung der Ebene E, in der die Platte liegt.
Stellen Sie die Platte, den Stab und die Lichtquelle in einem Koordinatensystem dar.
Berechnen Sie den Winkel zwischen dem Stab und der Platte.
(3 VP)
(Teilergebnis E: x 2 + 2x 3 = 6)
5
C
M
5
B
10
D F L
5
10
A
Eine Parametergleichung der Ebene ergibt sich durch die Punkte A, B und C.
10 −10 −10
E: x = ( 6 ) + r ∙ (
0
0
0
) + s ∙ ( −6 )
3
Der Normalenvektor dieser Ebene ergibt sich aus dem Kreuzprodukt ihrer
Richtungsvektoren.
−10 −10 0
0
n⃗ = ( 0 ) × ( −6 ) = ( 30) oder vereinfacht n⃗⃗⃗⃗ v = ( 1)
0 3 60
2

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Die Normalengleichung der Ebene lautet daher (Punkt A eingesetzt):
10 0
E: (x − p) ∙ n⃗ = (x − ( 6 )) ∙ ( 1) = 0
0 2
Durch Ausmultiplizieren dieser Gleichung ergibt sich die Koordinatengleichung der
Ebene.
E: x 2 + 2x 3 = 6
0
Der Stab hat den Richtungsvektor ( 0).
1
Der Winkel α zwischen dem Stab und der Platte ergibt sich aus
0 0
|( 1) ∙ ( 0)|
cos(90° − α) = sin(α) =
2 1
√1 + 4 ∙ √1 = 2 √5
⟹ α ≈ 63,4
Der Winkel α zwischen dem Stab und der Platte beträgt ca. 63,4°.
b) Der Stab wirft einen Schatten auf die Platte. Bestimmen Sie den Schattenpunkt des
oberen Endes des Stabes. Begründen Sie, dass der Schatten vollständig auf der
Platte liegt.
(3 VP)
Der Schattenpunkt entspricht dem Schnittpunkt der Ebene mit der Gerade g, die durch
die Punkte L und M verläuft.
8 −3
g: x⃗ = ( 10) + r ( −4)
2 0
Der Schnittpunkt der Gerade g mit der Ebene E: x 2 + 2x 3 = 6 ergibt sich aus
(10 − 4r) + 2 ∙ 2 = 14 − 4r = 6 ⟹ r = 2
Der Schattenpunkt der Stabspitze ist M* (2 | 2 | 2 ).
Der Schattenpunkt der Stabspitze ist M* liegt auf der Platte, da
1) die x 1 -Koordinate von M* zwischen den x 1 -Koordinaten von A und B liegt
und
2) die x 2 -Koordinate von M* zwischen den x 2 -Koordinaten von B und C liegt.

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Da der Punkt F direkt auf der Platte liegt, ist er sein eigener Schattenpunkt F*. Die
Schattenpunkte beider Stabenden liegen also auf der Platte. Daher liegt auch der
Schatten des Stabes vollständig auf der Platte.
c) Die Lichtquelle bewegt sich von L aus auf einer zur x 1 x 2 -Ebene parallelen Kreisbahn,
deren Mittelpunkt das obere Ende des Stabes ist. Dabei kollidiert die Lichtquelle mit
der Platte. Berechnen Sie die Koordinaten der beiden möglichen Kollisionspunkte.
(3 VP)
Da die Kreisbahn parallel zur x 1 x 2 -Ebene ist und durch den Punkt L verläuft, liegt die
Kreisbahn in der Ebene K: x 3 = 2. Hierdurch ergibt sich die x 3 -Koordinate der
Kollisionspunkte ebenfalls zu x 3 = 2.
Zusätzlich liegen die Kollisionspunkte auch in der Ebene E: x 2 + 2x 3 = 6. Durch
Einsetzten der x 3 -Koordinate ergibt sich die x 3 -Koordinate der Kollisionspunkte.
x 2 + 2 ∙ 2 = 6 ⟹ x 2 = 2
Hierdurch ergibt sich der allgemeine Kollisionspunkt K(k|2|2).
3
Der Radius der Kreisbahn ist |ML ⃗⃗⃗⃗⃗⃗ | = |( 4)| = √9 + 16 = 5.
0
Der Abstand vom Kollisionspunkt K(k|2|2) zum Mittelpunkt M(5|6|2) der Kreisbahn muss
ebenfalls 5m betragen.
k − 5 k − 5
|KG ⃗⃗⃗⃗⃗ | = |( 2 − 6)| = |( −4 )| = √(k − 5) 2 + (−4) 2 = 5
2 − 2 0
√(k − 5) 2 + (−4) 2 = 5 ⟹ (k − 5) 2 + (−4) 2 = 25 ⟹ (k − 5) 2 = 9 ⟹ k − 5 = ±3
k − 5 = 3 ⟹ k 1 = 8
k − 5 = −3 ⟹ k 2 = 2
Die beiden möglichen Kollisionspunkte sind K 1 (8|2|2) und K 2 (2|2|2).