Abitur 2015; Aufgabe B 2.1
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
© www.mathe-abi-bw.de Mathe-Abi<br />
Baden-Württemberg<br />
<strong>Abitur</strong> <strong>2015</strong>, <strong>Aufgabe</strong> B <strong>2.1</strong><br />
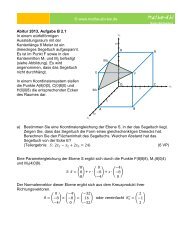
Gegeben sind die Ebene E: 3x 1 + 6x 2 + 4x 3 = 16 und eine Geradenschar durch<br />
5 a<br />
g: x⃗ = ( 1) + t ( 1) ; a ∈ R<br />
1 0<br />
a) Bestimmen Sie den Schnittpunkt der Geraden g 4 mit der Ebene E. Welche Gerade<br />
der Schar ist orthogonal zu g 4 ?<br />
(3 VP)<br />
Der Schnittpunkt von g 4 und E ergibt sich durch koordinatenweises Einsetzten der<br />
Geradengleichung mit a = 4 in die Ebenengleichung.<br />
E: 3(5 + 4t) + 6(1 + t) + 4(1) = 15 + 12t + 6 + 6t + 4 = 18t + 25 = 16 ⟹ t = −0.5<br />
Durch Einsetzten von t in die Geradengleichung ergibt sich der Schnittpunkt S(3|0,5|1).<br />
Die Geraden sind orthogonal wenn das Skalarprodukt ihrer Richtungsvektoren gleich Null<br />
ist.<br />
a 4<br />
( 1) ∙ ( 1) = 4a + 1 = 0 ⟹ a = − 1<br />
0<br />
4<br />
0<br />
Die Gerade g 1 −<br />
ist orthogonal zur Geraden g 4 .<br />
4<br />
b) Berechnen Sie den Schnittwinkel von g 4 und E.<br />
Für welche Werte von a mit −10 ≤ a ≤ 10 hat der Schnittwinkel von g a und E die<br />
Weite 10°?<br />
(3 VP)<br />
Der Schnittwinkel von g 4 und E lässt sich mit dem Richtungsvektor der Gerade und dem<br />
Normalenvektor der Ebene berechnen:<br />
4 3<br />
|( 1) ∙ ( 6)|<br />
cos(90° − α) = sin(α) =<br />
0 4<br />
√16 + 1 ∙ √9 + 36 + 16 = 18<br />
= 0,559 ⟹ α ≈ 34°<br />
√17 ∙ √61<br />
Für eine Schnittwinkel von 10° muss gelten:<br />
a 3<br />
|( 1) ∙ ( 6)|<br />
0<br />
sin(10°) =<br />
4<br />
√a 2 + 1 ∙ √61<br />
=<br />
|3a + 6|<br />
√a 2 + 1 ∙ √61
© www.mathe-abi-bw.de Mathe-Abi<br />
Baden-Württemberg<br />
Der Schnittwinkel von g a und E hat die Weite 10° für a 1 ≈ −3,76 und a 2 ≈ −1,27.<br />
c) Begründen Sie, dass alle Geraden g a in der Ebene F: x 3 = 1 liegen.<br />
Es gibt eine Gerade h, die durch den Punkt P(5|1|1) geht und in F liegt, aber nicht zur<br />
Schar gehört. Bestimmen Sie eine Gleichung der Geraden h.<br />
(3 VP)<br />
5 a<br />
Für jeden Punkt der Geradenschar g: x⃗ = ( 1) + t ( 1) gilt: x 3 = 1. Daher liegen alle<br />
1 0<br />
Geraden g a in der Ebene F: x 3 = 1.<br />
Für jede Gerade, die in der der Ebene F: x 3 = 1 liegt und durch den Punkt P geht gilt:<br />
r 1<br />
5<br />
h: x⃗ = ( 1) + t ( r 20 )<br />
1<br />
r 1<br />
Eine Gerade h gehört nicht zur Schar, wenn ihr Richtungsvektor ( r 20 ) kein Vielfaches von<br />
a<br />
( 1) ist. Diese Bedingung ist immer erfüllt mit r 2 = 0.<br />
0<br />
Eine der möglichen Geradengleichungen lautet (mit r 2 = 0 und frei gewähltem a = 1):<br />
5 1<br />
h: x⃗ = ( 1) + t ( 0)<br />
1 0