Trainingsaufgaben zur Klausurvorbereitung in Statistik I und II ...

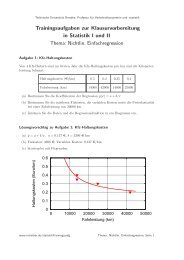
Technische Universität Dresden, Professur für Verkehrsökonometrie und -statistikAufgabe 3: SchwarzfahrerIn Dresden wird im Mittel zu 10% Schwarzgefahren. 70% der Schwarzfahrer haben keine Fahrkarte,während die anderen 30% gefälschte oder illegal besorgte Karten besitzen. Von denehrlichen Fahrgästen haben im Mittel 5% ihre Fahrkarte vegessen. Mit welcher Wahrscheinlichkeitist ein kontrollierter Fahrgast, der keine Karte vorzeigen kann, ein Schwarzfahrer?(Lösung: 7/11.5=61%)Lösungsvorschlag zu Aufgabe 3: SchwarzfahrerAus der Aufgabe ergeben sich die folgenden Wahrscheinlichkeiten:P(S = Schwarzfahrer) = 1 10 ,P(K = keine Karte|S) = 7 10 ,P(F = falsche Karte|S) = 3 10 ,P(K|E = ehrliche Fahrgäste) = 0.05.Uns interessiert das Ereignis P(Schwarzfahrer|keine Karte), was sich nach Bayes auch ausdrückenlässt alsP(K|S) · P(S)P(S|K) = . (1)P(K)Wir brauchen dafür P(K), also die totale Wahrscheinlichkeit über die disjunkte Zerlegungder ehrlichen Fahrgäste und der Schwarzfahrer:P(K) = P(K|E)P(E) + P(K|S)P(S) = 0.05 · 0.9 + 0.7 · 0.1 = 0.115, (2)so dass sich als Ergebnis ergibtP(S|K) =0.7 · 0.10.115≈ 60.8%. (3)www.mtreiber.de/statistikTrainingsaufg Thema: Satz von Bayes, Seite 4

Technische Universität Dresden, Professur für Verkehrsökonometrie und -statistikZeitKontrollierte Fahgäste9010ehrlichSchwarzfahrer95 5 30 70Karte86.5%KeineKarte4.5%KarteKeineKarte3% 7%Aufgabe 4: Disco oder: Ein Standardproblem für HeranwachsendeEs sei eine Disco mit 4 Floors gegeben und die “Flamme” ist an einem beliebig herausgegriffenenTag mit Wahrscheinlichkeit p in der Disco, d.h. in einen der 4 Floors. Der Typ hatnull Peil über den Musikgeschmack seiner Flamme und fragt sich nach vergeblicher Suchein 3 der Floors, mit welcher Wahrscheinlichkeit w er sie im letzten Floor doch noch trifft.Berechnen Sie w. Für welchen Wert von p trifft er sie auf jeden Fall im 4. Floor? Und: Fürwelches p ist die Chance zumindest bei 50%?Lösungsvorschlag zu Aufgabe 4: DiscoLösung mit dem Satz von Bayes lautetw = 1 4p −3Für p → 1 ergibt sich w → 1. Also für p = 1 ist die Flamme im letzten Floor anzutreffen.Weiterhin ergibt sichw ! = 0.5 −→ p = 4 5 . (4)Nun zu der Herleitung mit Satz von Bayes: Wir definieren die Ereignisse• A=”Flamme in Disco” mit P(A) = p• B=”Flamme in den ersten 3 Floors getroffen”www.mtreiber.de/statistikTrainingsaufg Thema: Satz von Bayes, Seite 5

Technische Universität Dresden, Professur für Verkehrsökonometrie und -statistikWegen der fehlenden Ahnung vom Musikgeschmack gelten fürderhin die bedingten Wahrscheinlichkeitenund natürlichP(B|A) = 3/4, P( ¯B|A) = 1/4P(B|Ā) = 0.(Wenn nicht in Disco, dann auch nicht auf einen der ersten drei Floors). Daraus ergibt sichsofort auch das komplementäre Ereignis P( ¯B|Ā) = 1. Die ”totale Wahrscheinlichkeit” istP( ¯B) = P(A)P( ¯B|A) + P(Ā)P( ¯B|Ā) = p + (1 − p). (5)4Gesucht ist die bedingte WahrscheinlichkeitAus dem Multiplikationssatz der Wahrscheinlichkeitenergibt sich der Satz von Bayesw = P(A| ¯B). (6)P(A ∩ B) = P(A)P(B|A) = P(B)P(A|B)P(A|B) = P(B|A)P(A)P(B)(7)und damitw =P( ¯B|A)P(A)P( ¯B)= 1 q.e.d. (8)− 3,4pLösungsvorschlag zu Aufgabe 4a: Lösung über ElementarereignisseDie Elementarereignisse sind:A 0 : Freundin nicht in DiskoA i : Freundin in Raum i ∈ 1, 2, 3, 4.Offenbar sind alle komplementär. Wir sind interessiert an dem Ereignis A = A 4 . Weiterhingibt für das Ereignis aus dem vorigen Abschnitt B = A 1 ∩ A 2 ∩ A 3 = A 0 ∪ A 4 . Damit ergibtsichP(A|B) ==P(A ∩ B)P(B)P(A 4 )P(A 0 ) + P(A 4 ) == P(A 4 ∩ (A 4 ∪ A 0 ))P(A 0 ∪ A 4 )p41 − p + p 4= 14p − 3.www.mtreiber.de/statistikTrainingsaufg Thema: Satz von Bayes, Seite 6

Technische Universität Dresden, Professur für Verkehrsökonometrie und -statistikAufgabe 5: KrankheitEine Krankheit kommt bei ca. 5% der Bevölkerung vor. Ein Test zur Erkennung der Krankheitführt bei 99% der Kranken zu einer Reaktion, aber auch bei 2% der Gesunden. Wiegroß ist die Wahrscheinlichkeit, dass eine Person, bei der die Reaktion eintritt, die Krankheitwirklich hat?Lösungsvorschlag zu Aufgabe 5: KrankheitZum Selbermachen ...Aufgabe 6: Mit dem LKW in die TürkeiEine Speditionsfirma transportiert unter anderem Maschinenteile von Deutschland in dieTürkei (Wegstrecke: 4000 km). Da eine verzögerte Lieferung mit hohen Konventionalstrafenverbunden ist, ist vor jedem dieser Transporte eine Inspektion des LKW vorgesehen, diejedoch von den Fahrern aus Bequemlichkeit in 20% der Fälle nicht durchgeführt wird. OhneInspektion erleidet der LKW pro 1000 gefahrene km mit 3% Wahrscheinlichkeit eine Panne,die zu einer unzulässigen Verzögerung führt, mit Inspektion nur mit 0,5%.(a) Wie groß ist die Wahrscheinlichkeit mindestens einer Panne auf der 4000 km langenStrecke ohne und mit Inspektion?(b) Mit welcher Wahrscheinlichkeit hat ein auf der Strecke liegengebliebener Fahrer die Inspektionnicht durchgeführt ? Hinweis: Berechnen Sie zunächst die mittlere Pannenwahrscheinlichkeitdurch entsprechende Gewichtung der in (a) berechneten Wahrscheinlichkeiten(Lösung: 3,88%) und wenden Sie dann den Satz von Bayes an!(c) Neben Pannen gibt es mit P(D) = 1% Wahrscheinlichkeit andere Gründe, die zu unzulässigenVerzögerungen führen wie z.B. Zoll oder Verkehrsstaus. Mit welcher Wahrscheinlichkeitkommen die Maschinenteile verspätet an?Lösungsvorschlag zu Aufgabe 6: Mit dem LKW in die TürkeiPannenwahrscheinlichkeit: Es seien folgende Ereignisse definiert:A: Inspektion wurde durchgeführtB: Es gab mindestens eine Panne auf der Fahrt in die TürkeiC: Es gab mindestens eine Panne auf 1000 km FahrtBekannt ist die unbedingte (totale) WahrscheinlichkeitP(A) = 0.8,sowie die bedingten WahrscheinlichkeitenP(C|A) = 0.005 Pannenwahrscheinlichkeit pro 1000 km bei durchgeführter InspektionP(C|Ā) = 0.03 Pannenwahrscheinlichkeit pro 1000 km, falls die Inspektion nicht durchgeführtwurdewww.mtreiber.de/statistikTrainingsaufg Thema: Satz von Bayes, Seite 7

Technische Universität Dresden, Professur für Verkehrsökonometrie und -statistikDa die Pannenwahrscheinlichkeit nicht vom Streckenabschnitt bzw. von schon erlittenenPannen abhängt, gilt für die Wahrscheinlichkeit, mit (A) oder ohne (Ā) Inspektion keinePanne zu erleiden:P( ¯B|A) = (1 − P(C|A)) 4 = (1 − 0.005) 4bzw.P( ¯B|Ā) = (1 − P(C|Ā))4 = (1 − 0.03) 4Damit ergibt sich für die Wahrscheinlichkeiten, mindestens eine Panne zu erleiden:P(B|A) = 1 − P( ¯B|A) = 1 − (1 − 0.005) 4 = 1.985%,P(B|Ā) = 1 − P( ¯B|Ā) = 1 − (1 − 0.03)4 = 11.47%Inspektionswahrscheinlichkeit: Unbedingte (totale) Wahrscheinlichkeit P(B):P(B) = ∑ kP(B|A k )P(A k ) = P(B|A)P(A) + P(B|Ā)P(Ā) = 0.0388Hier wurde A 1 = A und A 2 = Ā gesetzt.Die gesuchte Wahrscheinlichkeit P(Ā|B) ergibt sich mit dem Satz von Bayes (mit A k =A 2 = Ā):P(B|Ā)P(Ā) 0.1147 ∗ 0.2P(Ā|B) = = = 0.59P(B) 0.0388Während die a-priori-Wahrscheinlichkeit, keine Inspektion durchgeführt zu haben, nur P(Ā) =0.2 beträgt, steigt sie auf P(Ā|B) = 59%, wenn man die zusätzliche Information hat, dasseine Panne vorliegt.Verspätungswahrcheinlichkeit Sei Ereignis D: ”Sonsiger Grund für Verspätung”. Danngilt für Ereignis E = D ∪ B: ”Machinenteile kommen verspätet an” bei Unabhängigkeit dersonstigen Ursachen wie Zoll etc. von den Pannen:P(E) = P(D ∪ B) DeMorgan= 1 − P( ¯D Unabhh.∩ ¯B) = 1 − P( ¯D)P( ¯B) = 1 − 0.99 ∗ 0.9612 = 4.84%www.mtreiber.de/statistikTrainingsaufg Thema: Satz von Bayes, Seite 8