Kapitel 6: Viereckslehre 6.1 Haus der Vierecke Ordnung in der ...
Kapitel 6: Viereckslehre 6.1 Haus der Vierecke Ordnung in der ...
Kapitel 6: Viereckslehre 6.1 Haus der Vierecke Ordnung in der ...
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
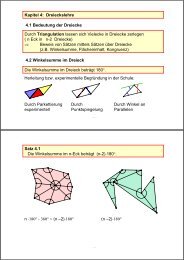
<strong>Haus</strong> <strong>der</strong> <strong>Vierecke</strong> 1<strong>Kapitel</strong> 6: <strong>Viereckslehre</strong><strong>6.1</strong> <strong>Haus</strong> <strong>der</strong> <strong>Vierecke</strong><strong>Ordnung</strong> <strong>in</strong> <strong>der</strong> Menge <strong>der</strong> <strong>Vierecke</strong>:1.Nach <strong>der</strong> Anzahl und Art <strong>der</strong> Symmetrien.2.nach Art, Anzahl und Lage gleichlanger Seiten, gleich großer W<strong>in</strong>kel,W<strong>in</strong>kel zwischen Diagonalen.Nicht so systematisch, aber für die Schule besser geeignet.Das „<strong>Haus</strong> <strong>der</strong> <strong>Vierecke</strong>“:Symmetrie als <strong>Ordnung</strong>spr<strong>in</strong>zipWelche <strong>Vierecke</strong>fehlen hier?Will man dasallgeme<strong>in</strong>e Trapezund denschiefen Drachen<strong>in</strong> das „<strong>Haus</strong>“aufnehmen, dannmuss manSchrägspiegelsymmetrieberücksichtigen.<strong>Haus</strong> <strong>der</strong> <strong>Vierecke</strong> 2
<strong>Haus</strong> <strong>der</strong> <strong>Vierecke</strong> 3W<strong>in</strong>kelsumme<strong>Haus</strong> <strong>der</strong> <strong>Vierecke</strong>1 Bestimmungsstück2 Bestimmungsstücke3 Bestimmungsstücke4 Bestimmungsstücke5 Bestimmungsstücke6.2 W<strong>in</strong>kelsumme im Viereck• Zerlegung <strong>in</strong> Dreiecke („Triangulation“)• experimentell gew<strong>in</strong>nbar z.B. beim Parkettieren (Punktspiegelungenund Verschiebung)
Sehnenvierecke 1Sehnenvierecke 26.3 <strong>Vierecke</strong> mit Umkreis („Sehnen-Viereck“)Witwe BolteOffensichtlich besitzt nicht jedes Viereck e<strong>in</strong>en Umkreis!Charakterisiere die <strong>Vierecke</strong> mit Umkreis!Satz <strong>6.1</strong>E<strong>in</strong> Parallelogramm hat genau dann e<strong>in</strong>en Umkreis, wenn es e<strong>in</strong>Rechteck ist. (Satz des Thales)DCABDas Viereck ABCD möge e<strong>in</strong>en Umkreisbesitzen.Verb<strong>in</strong>de die Eckpunkte mit dem Mittelpunkt.αββγ⇒ vier gleichschenklige Dreiecke mitgleichen Basisw<strong>in</strong>keln.Die Summe e<strong>in</strong>an<strong>der</strong> gegenüber liegen<strong>der</strong>W<strong>in</strong>kel ist also jeweils α+β+γ+δ .AαδδγBKürzerer Beweis:Verwende den Satz vom Umfangsw<strong>in</strong>kel über e<strong>in</strong>er DiagonalenSatz 6.2E<strong>in</strong> Viereck besitzt genau dann e<strong>in</strong>en Umkreis, wenn zweigegenüberliegende W<strong>in</strong>kel zusammen 180° groß s<strong>in</strong>d.
Sehnenvierecke 3TangentenviereckeDie Summe gegenüber liegen<strong>der</strong> W<strong>in</strong>kelzusammen betrage 180°.AKDZu zeigen: Das Viereck hat e<strong>in</strong>en Umkreis.Sei K <strong>der</strong> Umkreis des Dreiecks ABC.Für D’ auf K ist die Summe β+δ‘ = 180°Liegt D nicht auf K, dann ist δ kle<strong>in</strong>er o<strong>der</strong>größer als δ’, also β+δ ≠180°Bβδ’CD'δ6.4 <strong>Vierecke</strong> mit Inkreis („Tangenten-Viereck“)Offensichtlich besitzt nicht jedes Viereck e<strong>in</strong>en Inkreis!Charakterisiere die <strong>Vierecke</strong> mit Inkreis!Satz 6.3E<strong>in</strong> Viereck besitzt genau dann e<strong>in</strong>en Inkreis, wenn die Summe <strong>der</strong>Längen gegenüberliegen<strong>der</strong> Seiten gleich groß ist.Das Viereck möge e<strong>in</strong>en Inkreis besitzen.Dann ist die Summe <strong>der</strong> Längengegenüber liegen<strong>der</strong> Seiten offensichtlicha+b+c+d.addccJetzt sei die Summe <strong>der</strong> Längengegenüber liegen<strong>der</strong> Seiten gleich.Zu zeigen: das Viereck hat e<strong>in</strong>en Inkreis. Übung.abb
Mittenviereck6.5 Mitten-ViereckSatz 6.4Die Mitten <strong>der</strong> Seiten e<strong>in</strong>es Vierecks bilden stets e<strong>in</strong> Parallelogramm.DM 1M 2CBABeweis: Satz vom Mittendreieck.