DA - Fachgebiet Hochspannungstechnik

6 BEANSPRUCHUNGEN DURCH ELEKTRISCHE FELDER Seite 1 

6 Beanspruchungen durch elektrische Felder........................................................................2 

6.1 Einleitung ...................................................................................................................2 

6.2 Grundlagen des elektrischen Feldes ...........................................................................5 

6.3 Analytische Auswertung der Kontinuitätsgleichung................................................11 

6.3.1 Kugel frei im Raum ..........................................................................................12 

6.3.2 Konzentrische Kugeln (Kugelkondensator) .....................................................14 

6.3.3 Koaxiale Zylinder.............................................................................................18 

6.3.4 Homogenes Feld (Plattenkondensator).............................................................21 

6.4 Regeln für die grafische Feldermittlung...................................................................23 

6.5 Ausnutzungsfaktoren nach Schwaiger .....................................................................26 

Fachgebiet Hochspannungstechnik Hochspannungstechnik 

Prof. Dr.-Ing. Volker Hinrichsen WS 07/08 + SS 08


6 Beanspruchungen durch elektrische Felder 

6.1 Einleitung 

Zur Beurteilung der elektrischen Festigkeit einer Isolieranordnung ist die Kenntnis des 

elektrischen Feldes bei Anlegen einer Spannung an diese Anordnung von zentraler Bedeutung. 

Dabei sind sowohl deren örtlicher Verlauf als auch der Wert der maximal auftretenden 

Feldstärke wichtig. Diese werden, neben anderen Einflussfaktoren, ganz maßgeblich durch 

die Formgebung der Elektroden beeinflusst. Durch sie kann die Durchschlagfestigkeit einer 

Anordnung bei gegebener Schlagweite und gegebenem Dielektrikum in weiten Grenzen verändert 

werden, wie das folgende einfache Beispiel zeigt: 

I 1 

I 2 

E 

Anordnung 1 

E 2 max 

E 1 max 

U 1 

Anordnung 2 

U 2 

s 

x 

Zum unterschiedlichen Durchschlagverhalten bei homogenem und stark inhomogenem elektrischen Feld 

An zwei unterschiedliche Anordnungen 1 und 2 gleicher Schlagweite s werde eine langsam 

ansteigende Spannung angelegt. Anordnung 1 wird aus zwei Plattenelektroden gebildet, 

Anordnung 2 aus einer Spitze, die einer Platte gegenübersteht. An Anordnung 1 kommt es bei 

Erreichen der Spannung Ud1 (der Durchschlagspannung dieser Anordnung) zu einem plötzlichen 

Spannungszusammenbruch, verbunden mit dem plötzlichen Auftreten eines Stromes. 

An Anordnung 2 beginnt bereits bei vergleichsweise niedriger Spannung Ua ein sehr kleiner 

Strom zu fließen, und bei einer Spannung Ud2 wesentlich unterhalb Ud1 erfolgt der Span- 

nungszusammenbruch, verbunden mit einem starken Stromanstieg. Die Spannung Ua wird 

Anfangsspannung genannt, bei deren Erreichen Vorentladungen (Teilentladungen) 

U 1 


Prof. Dr.-Ing. Volker Hinrichsen WS 07/08 + SS 08 

I 1 

U 2 

I 2 

Ua 

U d2 

U d1 

t 

t 

t 

t


unmittelbar vor der Spitze einsetzen. Diese stellen einen Teildurchbruch der Isolierstrecke 

dar. Der Unterschied zwischen den beiden Anordnungen besteht in den Verläufen des elektrischen 

Feldes. In Anordnung 1 herrscht an jedem Ort innerhalb der Isolierstrecke gleiche Feldstärke, 

es handelt sich um ein homogenes Feld. Anordnung 2 weist dagegen ein stark inhomogenes 

Feld auf, das unmittelbar vor der Spitze die höchste Feldstärke aufweist, die mit 

zunehmendem Abstand sehr schnell abnimmt. 

Die beiden Anordnungen haben also trotz gleicher Schlagweiten sehr unterschiedliche 

Durchschlagspannungen, deren Ursache in den sich stark unterscheidenden Feldverläufen und 

maximalen Feldstärken zu suchen ist. 

Die Durchschlagfeldstärke Ed ist die maximale Feldstärke in einer Isolieranordnung bei 

der Durchschlagspannung Ud. Die Anfangsfeldstärke Ea ist die maximale Feldstärke in einer 

Isolieranordnung bei der Anfangsspannung Ua. Mit Hilfe dieser Begriffe lässt sich eine grobe 

Einteilung der Isolieranordnungen bzw. der bei ihnen vorliegenden Felder vornehmen: 

Homogenes Feld: Ed = Ud/s 

Schwach inhomogenes Feld: Ea = Ed = Emax(x) > Ud/s bei U = Ud 

Stark inhomogenes Feld: Ea = Emax(x) < Ed bei U = Ua 

Das schwach inhomogene Feld ist dadurch gekennzeichnet, dass es zwar bei Erreichen einer 

Feldstärke, die höher ist als die in einer vergleichbaren homogenen Anordnung, auch zu 

Vorentladungen kommt, dass sich daraus aber unmittelbar ein vollkommener Durchschlag 

entwickelt. Anfangs- und Durchschlagspannung sind identisch. 

Die Durchschlagfeldstärke Ed im homogenen bzw. schwach inhomogenen Feld (bei der es 

also zu einem vollkommenen Durchschlag kommt) sowie die Anfangsfeldstärke Ea im stark 

inhomogenen Feld (Beginn von Teildurchschlägen oder unvollkommenen Durchschlägen) 

wird auch als Durchschlagfestigkeit bezeichnet. Die Dimensionierung von Isolieranordnungen 

in Hochspannungsgeräten ist deshalb so schwierig, weil die Durchschlagfestigkeit von 

einer Vielzahl von zwar physikalisch begründbaren, in vielen Fällen jedoch nur empirisch 

gefundenen Parametern abhängt. Die Prinzipdarstellung auf der nächsten Seite vermittelt einen 

groben Überblick über die verschiedenen Abhängigkeiten. Unabhängig davon bleibt jedoch 

die Kenntnis elektrischer Feldverläufe der Schlüssel zur Konstruktion funktionstüchtiger 

hochspannungstechnischer Geräte. In vielen Fällen genügen dabei Abschätzungen anhand 

einfacher, analytisch zu berechnender ähnlicher Geometrien, und nicht selten ist bereits die 

Kenntnis der in der Anordnung auftretenden maximalen Feldstärke ausreichend. Das soll Gegenstand 

dieses Kapitels sein, während die exakte Berechnung auch komplizierter Feldgeometrien 

mit Hilfe von Feldberechnungsprogrammen an anderer Stelle behandelt wird. 




Qualitativer Verlauf der Durchschlagfestigkeiten von Isolieranordnungen in 

Abhängigkeit von verschiedenen Parametern 




6.2 Grundlagen des elektrischen Feldes 

Das elektrische Feld beschreibt einen physikalischen Zustand des Raumes. Es wird über 

die von ihm ausgehende Kraftwirkung auf elektrische Ladungen definiert. Grundsätzlich ist 

zwischen zwei Arten elektrischer Felder zu unterscheiden (Bild): 

Elektrisches Quellenfeld (links) und Wirbelfeld (rechts) 

Im Quellenfeld haben alle Feldlinien einen Anfangs- und einen Endpunkt (der auch im 

Unendlichen liegen kann). Die Anfangs- und Endpunkte werden durch positive und negative 

elektrische Ladungen gebildet. 

Im Wirbelfeld sind alle Feldlinien in sich geschlossen, besitzen also weder Anfangs- noch 

Endpunkte. Elektrische Wirbelfelder bilden sich beispielsweise um die Feldlinien eines zeitlich 

veränderlichen magnetischen Feldes aus. 

Die elektrische Feldstärke E 1 ist definiert über die Kraftwirkung F auf eine positive 

Probeladung q + : 

E = F/q + bzw. F = q + · E 

Die Richtung der elektrischen Feldstärke entspricht der Richtung der Kraft auf die positive 

Probeladung (Bild). 

q + q + 

+ 

F 

Die elektrische Feldstärke ist nicht nur von der sie verursachenden Ladung abhängig, sondern 

auch von den Stoffeigenschaften des Raumes, in dem sie wirkt. Über die Stoffeigen- 

1 Vektoren werden in diesem Skript fett und kursiv dargestellt. 



F 

q- q E 

- E 

Richtungen der Kräfte auf Probeladungen im elektrischen Feld


schaften ist sie mit einer materialunabhängigen Feldgröße, der elektrischen Verschiebungsdichte 

D, verknüpft: 

D = ε0·εr·E 

In isotropen 1 Stoffen, von denen hier grundsätzlich ausgegangen wird, besitzen die elektrische 

Verschiebungsdichte und die elektrische Feldstärke gleiche Richtung. Der Betrag 

D von D entspricht an der Oberfläche einer ideal leitenden Elektrode der Flächenladungsdichte 

σ und hat dementsprechend die Einheit As/m 2 bzw. C/m 2 : 

dq 

D =σ= 

dA 

Die die beiden Feldgrößen verknüpfende Stoffkonstante setzt sich zusammen aus der 

elektrischen Feldkonstanten (Dielektrizitätskonstante des Vakuums) 

ε 

0 

= 

8, 

8542⋅10 

−12 

As 

Vm 

= 8 

, 8542 

pF 

m 

und der relativen Dielektrizitätszahl εr. Die relative Dielektrizitätszahl hat grundsätzlich 

Werte ≥ 1. Die folgende Tabelle nennt Werte der relativen Dielektrizitätszahlen einiger für 

praktische Anwendungen wichtiger Stoffe: 

Tabelle einiger relativer Dielektrizitätszahlen 

Eine Ladung q, die gegen die Kraft des elektrischen Feldes von einem Punkt s1 nach s2 bewegt 

wurde, besitzt eine potentielle Energie Wpot. Über diese wird das Potential ϕ definiert: 

1 isotrop � richtungsunabhängige physikalische und chemische Eigenschaften 




s2 

ds 

W ∫ 

q q 

F 

pot s1 

ϕ= = 

Flächen gleichen Potentials im elektrischen Feld werden als Äquipotentialflächen bezeichnet. 

Sie stehen grundsätzlich senkrecht auf den Feldlinien, da nur in dieser Richtung eine 

Verschiebung von Ladungen ohne Energieaufwand möglich ist. Äquipotentialflächen, bzw. in 

zweidimensionaler Darstellung Äquipotentiallinien, sind das wichtigste und übliche Hilfsmittel 

zur anschaulichen grafischen Darstellung der elektrischen Feldverhältnisse an Hochspannungsgeräten. 

Das Potential muss auf eine (frei wählbare) Bezugsebene ϕ = 0 bezogen werden. Häufiger 

wird aber die Potentialdifferenz ∆φ zwischen zwei Punkten, gleichbedeutend mit der elektrischen 

Spannung U zwischen diesen Punkten angegeben: 

∆φ21 = U21 

Die Spannung zwischen zwei Punkten ergibt sich – im Quellenfeld unabhängig von der 

Wahl des Integrationsweges – als das Linienintegral der elektrischen Feldstärke längs des 

Weges s: 

∆W 

1 1 

∫ ∫ 

Fds q⋅Eds U21 =∆ϕ 21 = 

pot,21 2 = 

q q 

2 = 

q 

1 

= ∫ E ds 

2 

Ist also die räumliche Verteilung des elektrischen Feldes E(x,y,z) bekannt, so kann daraus 

die Potentialverteilung ϕ(x,y,z) abgeleitet werden. Umgekehrt ergibt sich bei gegebener Potentialverteilung 

das elektrische Feld zu 1 

⎧∂ϕ ∂ϕ ∂ϕ 

⎫ 

E(x,y,z) = {Ex, Ey, Ez} = – grad ϕ = – ⎨ , , ⎬ . 

⎩∂x∂y ∂z 

⎭ 

Das elektrische Quellenfeld wird, wie bereits erwähnt, durch Ladungen auf Elektrodenoberflächen 

erzeugt. Eine Elektrodenanordnung kann bei einer gegebenen anliegenden Spannung 

eine bestimmte Ladungsmenge auf ihren Oberflächen speichern. Dieses Speichervermögen 

ist die Kapazität C der Anordnung: 

q q 

C = = 

U ∆ϕ 

Für die Berechnungen bestimmter Auswirkungen des elektrischen Feldes lässt sich eine 

ausgedehnte Feldanordnung oft nutzbringend durch eine konzentrierte Kapazität ersetzen 

(nächstes Bild). So können z.B. viele Aspekte des Betriebsverhaltens von Betriebsmitteln in 

1 Die Gleichung ist hier für das kartesische Koordinatensystem angegeben. Häufig hat man es in der 

Hochspannungstechnik mit rotationssymmetrischen Anordnungen zu tun. In diesen Fällen wird man die 

Berechnungen zweckmäßigerweise in einem Kugel- oder Zylinderkoordinatensystem durchführen. 




der elektrischen Energieversorgung durch die Abschätzung von Erdkapazitäten oder Streukapazitäten 

behandelt werden. Im Gegensatz zu elektrischen Feldbildern und Feldstärken 

lassen sich diese parasitären Kapazitäten unmittelbar in Netzwerkberechnungsprogrammen 

verarbeiten (z.B. zur Ermittlung der Spannungsverteilung entlang Isolatoren, Stützern, Spannungsteilern, 

Überspannungsableitern). 

Von den Maxwellschen Gleichungen für ruhende Körper werden für die meisten hochspannungstechnischen 

Probleme nur wenige und diese teilweise in vereinfachter Form benötigt, 

da in der Regel mit genügender Genauigkeit von elektrostatischen stationären oder quasistationären 

Quellenfeldern ausgegangen werden kann. Trotzdem werden die Gleichungen an 

dieser Stelle kurz angeführt, um anschließend auf die Vereinfachungen einzugehen. Grundsätzlich 

unterscheidet man 

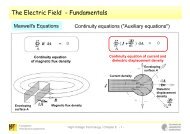
- zwei Feldgleichungen ("Hauptgleichungen"): Zusammenhang zwischen zeitveränderlichen 

elektrischen und magnetischen Größen � Induktionsgesetz, Durchflutungsgesetz; 

- zwei Kontinuitätsgleichungen ("Nebengleichungen"): Quellen der Feldgrößen � 

Kontinuitätsgleichung für die magnetische Flussdichte, Kontinuitätsgleichung für 

Leitungs- und Verschiebungsstromdichte; 

- drei Stoffgleichungen: Einfluss verschiedener Materialeigenschaften auf den Zusammen- 

hang zwischen den Feldgrößen. 

Kapazität eines elektrischen Quellenfeldes 

Üblich ist die Darstellung dieser Gleichungen entweder in differentieller oder in integraler 

Form. Hier erfolgt eine Beschränkung auf die integrale Form. Auf der nächsten Seite sind die 

Gleichungen zusammen mit einer anschaulichen Darstellung ihres physikalischen Hintergrundes 

zusammengestellt 1 . Für die Hochspannungstechnik von besonderer Bedeutung sind (im 

Bild fett eingerahmt) 

- das Induktionsgesetz, 

- die Kontinuitätsgleichung für Leitungs- und Verschiebungsstromdichte, 

- die Stoffgleichung für die elektrische Verschiebungsdichte. 

1 nach: A. Küchler, Hochspannungstechnik, VDI-Verlag, 2005 




Die beiden Maxwellschen Hauptgleichungen (Integralform) für ruhende Körper 

E ... elektrische Feldstärke; B ... magnetische Flussdichte; H ... magnetische Feldstärke; 

J ... Leitungsstromdichte; D ... elektrische Verschiebungsdichte 

Die beiden Maxwellschen Nebengleichungen (Integralform) 

B ... magnetische Flussdichte; J ... Leitungsstromdichte; D ... elektrische Verschiebungsdichte 

Die drei Stoffgleichungen 

B ... magnetische Flussdichte; H ... magnetische Feldstärke; D ... elektrische Verschiebungsdichte; 

E ... elektrische Feldstärke; J ... Leitungsstromdichte; µ0 ... Permeabilitätskonstante des Vakuums; 

µr ... relativer Permeabilitätsfaktor; ε0 ... Dielektrizitätskonstante des Vakuums; 

εr ... relative Dielektrizitätskonstante; κ ... Leitfähigkeit 




∫∫ A 

Das Induktionsgesetz sagt aus, dass ein zeitlich veränderlicher magnetischer Fluss 

B d A ein elektrisches Wirbelfeld E induziert. Die Umlaufspannung längs des Flächenran- 

des der vom magnetischen Fluss durchsetzten Fläche entspricht der zeitlichen Ableitung des 

Flusses. Für die am häufigsten behandelten Probleme der Hochspannungstechnik – Anordnungen 

mit nichtleitenden Isolierstoffen bei Beanspruchung mit netzfrequenter Wechselspannung, 

Schalt- oder Blitzstoßspannungen – kann von langsam veränderlichen (quasi-stationären) 

kapazitiven Feldern ausgegangen werden. Das Induktionsgesetz vereinfacht sich 

dann zu 

∫� 

x 

E dx = 0. 

Die Kontinuitätsgleichung für Leitungs- und Verschiebungsstromdichte besagt, dass 

die durch die Hüllfläche A austretende gleich der in sie eintretenden Stromdichte ist, wenn 

sowohl Leitungs- als auch Verschiebungsstrom betrachtet werden. Der über einen Leiter auf 

eine Elektrode fließende Leitungsstrom it ( ) = ∫∫� J 

A 

dA 

setzt sich im nichtleitenden 

Dielektrikum als Verschiebungsstrom 

∂ 

∫∫� A ∂t 

d 

D Afort. Durch Integration der 

Kontinuitätsgleichung über der Zeit ergibt sich der Zusammenhang zwischen 

Verschiebungsdichte D und der von der Hüllfläche A eingeschlossenen Ladung: 

Kontinuitätsgleichung: 

⎛ ∂D 

⎞ 

∫∫ ⎜ J + ⎟ dA 

= 0 

A⎝ 

∂t 

⎠ 

∂D 

Umformung: �∫∫ dA=− d = it ( ) 

A ∂t 

�∫∫ 

J A 

A 

�∫∫ ∫ 

Integration über der Zeit: D d A = it ( ) dt 

= Q 

A 

Die letzte Gleichung wird als Satz vom Hüllenfluss bezeichnet und stellt eine wichtige 

Beziehung zur analytischen Feldberechnung in einigen grundsätzlichen, praktisch wichtigen 

geometrischen Anordnungen dar. Versteht man die Ladung Q als Integral über der Raumladungsdichte 

η in dem von der Hüllfläche eingeschlossenen Volumen (siehe Bild), so lässt 

Zum Satz vom Hüllenfluss 




sich der Satz vom Hüllenfluss auch schreiben als 

�∫∫ ∫∫∫ 

D dA= η dV. 

A V 

In differentieller Schreibweise lautet diese Gleichung 

div D = η . 

Mit D = ε·E und E = – grad ϕ (s. Seite 7) wird daraus 1 

div E = div (– grad ϕ) = η/ε 

und schließlich, mit div (grad ϕ) = ∆ϕ: 

∆ϕ = – η/ε (in kartesischen Koordinaten: 



2 2 2 

∂ ϕ ∂ ϕ ∂ ϕ 

+ + =−ηε 

) 

2 2 2 

∂x ∂y ∂z 

Dies ist die Poisson'sche Potentialgleichung für das raumladungsbehaftete Feld. Für 

den Spezialfall des raumladungsfreien Feldes (η = 0) wird daraus die Laplace'sche Potentialgleichung: 

∆ϕ = 0 (in kartesischen Koordinaten: 

∂ ϕ ∂ ϕ ∂ ϕ 

∂x ∂y ∂z 

2 2 2 

+ 2 + 2 = 0 2 

Elektrostatische, quasistationäre Felder sind durch die Poisson'sche oder die Laplace'sche 

Potentialgleichung eindeutig beschrieben. Deren Lösung, unter Anwendung unterschiedlicher 

Verfahren, ist daher grundsätzlich das Ziel von Feldberechnungen. 

Die Stoffgleichung für die elektrische Verschiebungsdichte schließlich berücksichtigt 

über den Faktor εr die Vergrößerung der der elektrischen Ladung proportionalen elektrischen 

Verschiebungsdichte durch die durch das elektrische Feld bewirkte elektrische Polarisation. 

Polarisation bedeutet Verschiebung vorhandener Ladungen bzw. Ausrichtung elektrischer 

Dipole. Da prinzipiell jede Materie mehr oder weniger stark polarisierbar ist, ist die relative 

Dielektrizitätszahl εr grundsätzlich größer als Eins. Wird einer Elektrodenanordnung eine 

Spannung bzw. eine elektrische Feldstärke eingeprägt, so wird in dieser Anordnung umso 

mehr Ladung gespeichert, je größer die relative Dielektrizitätszahl ist (Prinzip des Kondensators). 

6.3 Analytische Auswertung der Kontinuitätsgleichung 

Das elektrische Feld einfacher geometrischer (z.B. kugel- oder zylindersymmetrischer) 

Anordnungen, auf die viele kompliziertere Anordnungen in der Hochspannungstechnik zurückgeführt 

werden können, lässt sich in einfacher Weise durch die analytische Auswertung 

der Kontinuitätsgleichung (des Satzes vom Hüllenfluss) berechnen. Dazu wird in vier, ggf. 

fünf Schritten vorgegangen: 

1 Aus Gründen einer vereinfachten Schreibweise wird hier und im weiteren ε0εr durch den Ausdruck ε ersetzt. 

)


1. Schritt: Auflösung des Satzes vom Hüllenfluss D dA 

= Q nach dem Betrag von D. 

Es ergibt sich damit der Zusammenhang zwischen felderzeugender Ladung Q und dem 

örtlichen Verlauf des Betrages der elektrischen Feldstärke E = D/ε. 

2. Schritt: Ermittlung der Spannungsdifferenz durch Integration der Feldstärke längs des 

1 

Weges: U21 = ∫ E ds. 

Dies führt auf den Zusammenhang zwischen Ladung und Spannung: 

Q = f(U). 

2 

3. Schritt: Ermittlung der Kapazität der Anordnung: = Q 

C U 

4. Schritt: Ermittlung des Zusammenhanges zwischen Feldstärke E und Spannung U aus 

den Ergebnissen des ersten und des zweiten Schrittes: E = f(U). 

5. Schritt: Ermittlung der maximalen Feldstärke; Optimierungen, z.B. Maßnahmen zur 

Minimierung der maximalen Feldstärke 

Im Folgenden werden nach der oben beschriebenen Vorgehensweise einige typische Elektrodenanordnungen 

untersucht. 

6.3.1 Kugel frei im Raum 

Es wird von einer Punktladung mit unendlich weit entfernter Gegenladung ausgegangen. 

Als Hüllfläche wird eine Kugelfläche gewählt. Aufgrund der Symmetrie der Anordnung hat 

Feldverhältnisse an einer Kugelelektrode frei im Raum 

die elektrische Verschiebungsdichte D überall auf der Fläche im Abstand r den gleichen Betrag 

D(r). Da die Vektoren der elektrischen Verschiebungsdichte und der Fläche gleichgerichtet 

sind, ist weiterhin das Skalarprodukt D·dA gleich dem Produkt der Beträge D·dA. 

Damit wird im ersten Schritt aus dem Satz vom Hüllenfluss: 



∫∫� 

A


�∫∫ �∫∫ 

A 

D d A = () d = () ⋅ () = ()4π ⋅ = 

2 

Dr A Dr Ar Dr r Q 

A 

Für die Beträge der elektrischen Verschiebungsdichte und der Feldstärke ergibt sich also: 

Q 

Dr () = 2 

4πr 

Q 

Er () = 

4πεr 

2 

Im zweiten Schritt wird durch Integration der Feldstärke längs des Weges die Spannung 

zwischen der Kugeloberfläche mit dem Radius r = R und der unendlich weit entfernten Gegenladung 

ermittelt: 

∞ ∞ 

Q 1 Q ⎡ 1⎤ 

Q 

U = ∫E()d r r = dr 

= ⋅ − = 

4πε∫ r 4πε ⎢ 

⎣ r⎥ ⎦ 4πεR 

R∞ 2 

R R 

Unter der Annahme, dass U∞ = 0 ist, gilt also für die Ladung: 

Q = 4πεRU. 

Im dritten Schritt wird die Kapazität der Kugel ermittelt: 

Q 

C = = 4πε 

R, 

U 

und aus dem ersten und dem zweiten Schritt ergibt sich für den Zusammenhang zwischen 

Feldstärke und Spannung im vierten Schritt: 

R 

Er () = U⋅ . 2 

r 

E/E E/Emax max 

1 

0 

R 

Feldstärkeverlauf für Kugel frei im Raum 

Nun lässt sich im fünften Schritt beispielsweise die maximale Feldstärke berechnen, die 

an der Kugeloberfläche auftritt: 

E = E R = . 

R 

max ( ) U 

r 



∞ 

R


Eine praktische Anwendung dieser Betrachtungen wurde bereits in Kapitel 2 bei der Dimensionierung 

von Abschirmkörpern von Prüftransformatoren gezeigt. Es lassen sich so aber 

auch näherungsweise die Feldstärken an scharfkantigen Spitzen abschätzen, indem für den 

Kugelradius extrem kleine Werte angenommen werden. Hierbei ist allerdings zu beachten, 

dass die Herleitungen nur solange gültig sind, wie die Elektrode vorentladungsfrei bleibt. Das 

ist bei so extrem kleinen Durchmessern nur für sehr kleine Spannungen der Fall: es ergibt sich 

etwa für einen Kugelradius von 1 mm und eine anliegende Spannung von 3 kV bereits eine 

maximale Feldstärke Emax = 30 kV/cm. Bei dieser ist die Anordnung aber schon nicht mehr 

vorentladungsfrei. Das Beispiel belegt aber, welch niedrige Spannungen an scharfkantige 

Elektroden nur angelegt werden dürfen, wenn Vorentladungsfreiheit sichergestellt sein soll. 

6.3.2 Konzentrische Kugeln (Kugelkondensator) 

Wie für die Kugel frei im Raum, wird von einer Punktladung ausgegangen. Die Radien der 

innere und der äußeren Kugel bilden die Integrationsgrenzen. 

1. Schritt (identisch mit dem für die Kugel frei im Raum): 

�∫∫ �∫∫ 

A 

D d A = () d = () ⋅ () = ()4π ⋅ = 

Q 

Dr () = 2 

4πr 

Q 

Er () = 

4πεr 

2 

Dr A Dr Ar Dr r Q 

A 

2 

Feldverhältnisse für konzentrische Kugeln 




2. Schritt: 

RR 1 2 

R2 R2 

R2 

Q 1 Q ⎡ 1⎤ Q ⎛ 1 1 ⎞ Q R2 − R1 

∫ ()d d 2 

⎜ ⎟ 

4πε ∫ r 4πε ⎢ r⎥ R 4π R 

1 1 

1 

1 R2 4π R R R 

⎣ ⎦ ε ⎝ ⎠ ε 1⋅R2 U = E r r = r = ⋅ − = ⋅ − = ⋅ 

R1⋅R2 Q = 4πε 

U ⋅ 

R − R 

2 1 

3. Schritt: 

Q R1⋅R2 C = = 4πε 

⋅ 

U R − R 

2 1 

Einführung der Schlagweite s = R2 – R1: 

s+ R 

C = 4π R ⋅ 

s 

1 ε 1 . 

Darin stellt der Ausdruck 4πεR1 die Kapazität Ck einer Kugel frei im Raum mit dem Radius 

der inneren Kugel dar (s. Abschnitt 6.3.1), und es lässt sich die Kapazität des Kugelkondensators 

direkt mit der Kapazität einer Kugel frei im Raum vergleichen: 

⎞ 

C = C ⋅ ⎜ + ⎟ 

⎝ s ⎠ . 

1 

k 1 R ⎛ 

Die Kapazität der koaxialen Anordnung ist also grundsätzlich größer als die der Kugel frei 

im Raum. 

4. Schritt: 

Mit den Ergebnissen des ersten und des zweiten Schrittes ergibt sich der Feldstärkeverlauf 

zu: 

R ⋅ R 

1 

1 2 

Er () = U⋅ ⋅ 2 

R2 − R1 r 

Mit einer Abnahme mit 1/r 2 entspricht der Feldstärkeverlauf also qualitativ dem an der 

Kugel frei im Raum. 

5. Schritt: 

Die Maximalfeldstärke tritt an der Oberfläche der inneren Kugel auf, d.h. für den Fall 

r = R1: 

E 

max 

U R2 

= ⋅ 

R R − R 

1 2 1 

In dieser Gleichung stellt der Ausdruck U/R1 die Maximalfeldstärke Emax, k einer Kugel frei 

im Raum dar (s. Abschnitt 6.3.1), und wiederum ist ein direkter Vergleich beider Anordnungen 

möglich: 




R2 

Emax = Emax, 

k ⋅ . 

R − R 

2 1 

Die Maximalfeldstärke an der konzentrischen Kugelanordnung ist also grundsätzlich höher 

als an der Kugel frei im Raum. Ist beispielsweise der Radius R2 der äußeren Kugel fünfmal 

größer als der Radius R1 der inneren Kugel, so ergibt sich aus der obigen Gleichung eine 25 % 

höhere maximale Feldstärke. 

Setzt man in die vorletzte Gleichung für einen gegebenen Radius R2 der Außenkugel die 

beiden extremen Möglichkeiten für die Wahl von R1 ein, nämlich R1 → 0 und R1 → R2, so 

zeigt sich, dass in beiden Fällen die maximale Feldstärke gegen Unendlich strebt. Dazwischen 

muss also ein Minimum liegen, d.h. es muss einen Radius R1, opt der Innenkugel geben, für die 

die maximale Feldstärke minimal ist. Dieses Minimum lässt sich durch Nullsetzen der Ableitung 

der maximalen Feldstärke nach dem Radius R1 ermitteln (Anwendung von Produkt- und 

Quotientenregel): 

∂E ∂ ⎛ U R ⎞ U R U R 

= ⋅ =− ⋅ + ⋅ = 0 

∂ ∂ − − − 

max 2 2 2 

⎜ ⎟ 2 

2 

R1 R1⎝R1 R2 R1⎠R1 R2 R1 R1 ( R2 R1) 

Umformung und Auflösung nach R1 ergibt: 

R 

2 

2 R 1,opt = und durch Einsetzen von R1, opt: Emax,opt 



4U 

= 

R 

Ein weiterer interessanter Aspekt ergibt sich, wenn in der Gleichung für die maximale 

Feldstärke die Schlagweite s = R2 – R1 eingeführt wird: 

E 

U R U U 

R R R R s 

2 

max = ⋅ = + 

1 2 − 1 1 

mit s = R2 – R1 

In dieser Form der Gleichung kommt zum Ausdruck, dass sich die maximale Feldstärke 

aus zwei Bestandteilen zusammensetzt: der Term U/R1 entspricht der maximalen Feldstärke 

einer Kugel frei im Raum, der Term U/s ist die Feldstärke im homogenen Feld einer Elektrodenanordnung 

der Schlagweite s. Man kann daher von einem Krümmungseffekt und einem 

Abstandseffekt sprechen: 

Krümmungseffekt: 

U U U 

R > → E ≈ 

1 max 

R1 s R1 

Soll also in einer Anordnung mit R1


Abstandseffekt: 

U U U 

R >> s →


Das Bild (vorherige Seite) zeigt einige praktische Beispiele, in denen mit der Annahme 

von Kugel- oder konzentrischen Kugelfeldern auf einfache Weise grobe Abschätzungen und 

Optimierungen der günstigsten Radien und Schlagweiten vorgenommen werden können. 

6.3.3 Koaxiale Zylinder 

Koaxiale Zylinder stellen, etwa im Zusammenhang mit gasisolierten Schaltanlagen und 

Leitungen oder mit Kabeln, eine der wichtigsten grundsätzlichen Anordnungen in der Hochspannungstechnik 

dar. Auch sie lassen sich mit Hilfe des Satzes vom Hüllenfluss analysieren. 

Dazu wird von einer koaxialen Anordnung der Länge z (unter Vernachlässigung von Randeffekten 

an den Enden) und einer zylindrischen Hüllfläche mit dem Radius r ausgegangen. 

1. Schritt: 

�∫∫ �∫∫ 

A 

D d A = Dr () d A= Dr () ⋅ Ar () = Dr ()2π ⋅ rz= Q 

Q 

Dr () = 

2πrz 

Q 

Er () = 

2πε 

rz 

2. Schritt: 

R2 R2 

A 

Q 1 Q R2 

Q R 

URR = ∫ E( r) dr = dr = ⋅ [ ln r] 

= ⋅ln 

R 

2πεz∫ r 2πεz 2πεz 

R 

1 2 1 

R1 R1 

2πε 

z 

Q = ⋅U 

R2 

ln 

R 

3. Schritt: 

Q 2πε 

z 

C = = 

U R2 

ln 

R 

4. Schritt: 

U 

Er () = 

R 

r ⋅ln 

R 

5. Schritt: 

1 

1 

2 

1 

Die Maximalfeldstärke tritt an der Oberfläche des inneren Zylinders auf, d.h. für den Fall 

r = R1: 

U 

Emax = E1= 

R 

R1 

⋅ln 

R 

2 

1 



2 

1


Die Feldstärke an der koaxialen Zylinderanordnung nimmt also mit 1/r ab. Damit ergibt 

sich ein flacherer Kurvenverlauf als bei den konzentrischen Kugeln (dort: Abnahme mit 1/r 2 ). 

Auch die maximale Feldstärke ist bei gleichen Radienverhältnissen an der Zylinderanordnung 

grundsätzlich niedriger als an der Kugelanordnung. Das folgende Bild zeigt einen Vergleich: 

Wie auch für die konzentrischen Kugeln ergeben sich ins Unendliche anwachsende maximale 

Feldstärken für die Extremfälle des Durchmessers R1 → 0 und R1 → R2. Also muss es 

auch für diese Anordnung einen Radius R1, opt bzw. ein Radienverhältnis (R2/R1)opt geben, bei 

dem die an der Oberfläche des Innenzylinders auftretende maximale Feldstärke ein Minimum 

hat. Am einfachsten erhält man die Lösung durch Nullsetzen der Ableitung der maximalen 

Feldstärke nach dem Radienverhältnis R2/R1: 

E 

max 

U 

= 

R 

R1 

⋅ln 

R 

U 

= 

R 

R2 

R1 

⋅ 

R 

ln 

R 

2 2 2 

1 1 

⎛ R2 ⎞ R2 R2 R1 

1ln ⋅ − ⋅ 

∂Emax ∂ ⎜ U R ⎟ 

1 U R1 R1 R2 

= ⎜ ⋅ ⎟ = ⋅ = 0 

2 

⎛R ⎞ ⎛ R R 

2 R ⎞ 2 ⎜ 2 2 ln ⎟ R2 

∂ 

⎛ R ⎞ 2 

⎜ ⎟ ∂⎜ ⎟⎜ 

R ⎟ ln 

R1 R ⎜ ⎟ 

⎝ ⎠ ⎝ 1 ⎠⎝ 1 ⎠ 

⎝ R1 

⎠ 

⎛ R 

⎞ 

E 

U/R 1 

2 ln⎜ ⎟ = 1 

⎝ R1 

⎠opt 

konzentrische Kugeln 

Kugel frei im Raum 

koaxiale Zylinder 

(R 1 = 1) (R 2 = 5·R 1 ) 



r/R 1 

Relative Feldstärkeverteilungen im Vergleich: Kugel frei im Raum, 

konzentrische Kugeln, koaxiale Zylinder


⎛ R ⎞ 2 

⎜ ⎟ 

⎝ R ⎠ 

1 opt 

= e= 2,718 

R2 

R1,opt = = 0,368⋅ 

R2 

e 

Die maximale Feldstärke bei optimaler Bemessung der Radienverhältnisse ist 

E 

max,opt 

U U e ⋅U 

= = = 

⎛ R ⎞ R 2 

1,opt R2 

R1,opt 

ln⎜ 

⎟ 

⎝ R ⎠ 

1 opt 

Der Vergleich mit der maximalen Feldstärke im optimalen Fall der konzentrischen Kugel- 

⎛ 4U ⎞ 

anordnung ⎜ Emax,opt 

= ⎟ zeigt unmittelbar, dass die koaxiale Zylinderanordnung günstiger 

⎝ R2 

⎠ 

ist, d.h. niedrigere Maximalfeldstärken aufweist. 

Das nächste Bild gibt die Abhängigkeit der maximalen Feldstärke vom Radienverhältnis 

wieder. Wie bei den konzentrischen Kugeln verläuft das Minimum sehr flach, so dass das 

optimale Radienverhältnis zur Erzielung einer minimalen Maximalfeldstärke nicht genau eingehalten 

werden muss: 

E 1 

E 1, opt 

R 1 = R 2 /e 

R 1 /R 2 

Abhängigkeit der maximalen Feldstärke für koaxiale Zylinder in 

Abhängigkeit vom Radienverhältnis 

Tatsächlich zeigt sich, dass die Durchschlagspannung – das eigentliche Kriterium für die 

Auslegung einer koaxialen Anordnung – ihr Maximum bei einem etwas kleineren als dem 

optimalen Radienverhältnis hat. Man entscheidet sich daher in der Regel für Auslegungen 

R1/R2 ≤ 1/e. 




6.3.4 Homogenes Feld (Plattenkondensator) 

Auch das homogene Feld, wie es bei Vernachlässigung der Randeffekte zwischen den 

Elektroden eines Plattenkondensators vorliegt, lässt sich mit Hilfe des Satzes vom Hüllenfluss 

berechnen. Das folgende Bild zeigt die vorliegenden Verhältnisse, wobei die Änderung des 

Feldverlaufes im Randbereich nur angedeutet ist. 

Es wird eine Hüllfläche definiert, die die linke Elektrode vollständig umschließt. Sie besteht 

aus einer Fläche A zwischen den Elektroden und aus Flächen im äußeren Feldbereich, 

die aber von einem so geringen Verschiebungsfluss durchsetzt werden, dass er für die folgenden 

Betrachtungen vernachlässigt wird. Die verbleibende elektrische Verschiebungsdichte D 

hat die gleiche Richtung wie der Flächenvektor dA, so dass mit den Produkten der Beträge 

gerechnet werden kann. Weiterhin ist der Betrag D der elektrischen Verschiebungsdichte über 

die ganze Fläche A konstant, und die Integration von dA über der Fläche A ergibt den Wert 

der Fläche A selbst. Die 5 Berechnungsschritte sehen dann folgendermaßen aus: 

1. Schritt: 

�∫∫ �∫∫ 

A 

D dA = D dA= 

D⋅ A= Q 

Q 

D( x) = = const. 

A 

Q 

E( x) = = const. = E 

εA 

A 

0 

Die elektrische Feldstärke weist also über die gesamte Schlagweite einen konstanten Wert 

E0 auf. 

2. Schritt: 

Homogenes elektrisches Feld des Plattenkondensators 

(Randeffekte vernachlässigt) 

Integration der Feldstärke über die Schlagweite s ergibt die Spannung: 



s


s 

Q⋅s U = ∫ E( x) dx 

= E⋅ s= 

ε ⋅ A 

0 

ε ⋅AU ⋅ 

⇒ Q = 

s 

3. Schritt: 

Q ε ⋅ A 

C = = 

U s 

4. Schritt: 

Q U 

E( x) = = = const. 

ε ⋅ A s 

Der fünfte Schritt – Berechnung der Maximalfeldstärke – erübrigt sich. Im praktischen Fall 

kommt es am Rand des Plattenkondensators natürlich zu erheblichen Feldstärkeerhöhungen, 

die hier nicht detailliert untersucht werden sollen. Plattenkondensatoren werden daher aber in 

der Hochspannungstechnik mit verrundeten Rändern derart ausgeführt, dass die Feldstärke an 

keiner Stelle höher wird als im homogenen Teil. Dabei ist das so genannte Rogowski-Profil 

so bemessen, dass die Feldstärke nach außen hin stetig abnimmt, während das wegen seiner 

ökonomischeren Bauweise häufiger eingesetzte Borda-Profil überall gleiche Feldstärke ergibt. 

Borda-Profil (links) und Rogowski-Profil (rechts) Randfeld eines Plattenkondensators mit Borda-Profil 

An dem einfachen Beispiel des homogenen Teils des Plattenkondensators soll noch gezeigt 

werden, dass die Berechnung in vielen Fällen auch durch analytische Auswertung der 

Laplaceschen Potentialgleichung möglich ist, die sich hier wegen der fehlenden 

Abhängigkeiten von der y- und der z-Richtung wesentlich vereinfacht zu: 

2 

∂ ϕ 

∆ ϕ = = 0 2 

∂x 

Durch zweifache Integration ergibt sich: 

∂ ϕ 

= 

∂x 

k1 




ϕ ( x) = k ⋅ x+ k 

1 2 

Die Integrationskonstanten k1 und k2 werden aus den Randbedingungen bestimmt: 

ϕ ( x = 0) = U ⇒ U = k 

U 

ϕ ( x= s) = 0 ⇒ k1⋅ s+ k2 = 0 ⇒ k1 

=− 

s 

Daraus folgt für die Potentialverteilung: 

( ) 1 x ⎛ ⎞ 

ϕ x = U⎜ 

− ⎟ 

⎝ s ⎠ 

und für die Feldstärke: 

∂ϕ 

U 

E =− grad ϕ =− = = const. 

∂x 

s 

2 

6.4 Regeln für die grafische Feldermittlung 

Die bisher behandelten Beispiele betrafen Anordnungen, in denen sich aufgrund der einfachen 

Geometrien und Symmetrien auch einfache Feldverläufe ergeben. Reale Anordnungen 

sind in der Regel komplizierter. Deren Berechnung erfolgt heutzutage praktisch ausschließlich 

mit Feldberechnungsprogrammen. Insbesondere für zweidimensionale rotationssymmetrische 

Probleme sind mittlerweile Programme verfügbar, die auf jedem PC eingesetzt werden können. 

Aber auch dreidimensionale Anordnungen sind weitestgehend berechenbar, wenn auch 

mit großem zeitlichen Aufwand (dieser liegt hauptsächlich bei der Eingabe der Geometrien). 

Es macht trotzdem Sinn, sich mit einigen Grundregeln zur Erstellung eines Feldbildes von 

Hand vertraut zu machen. Dies verbessert einerseits das zur Interpretation der grafischen Ergebnisausgabe 

von Feldberechnungen erforderliche Verständnis, andererseits kann man sich 

auf diese Weise mit einfachen Hilfsmitteln schnell ein grobes Bild der Feldverhältnisse an 

Zur grafischen Ermittlung von Feld- und Äquipotentiallinienverläufen 




beliebigen Elektrodenanordnungen machen. Die Anwendung ist allerdings auf ebene, das 

heißt zweidimensionale Probleme beschränkt. 

Es gelten folgende "Zeichenregeln" (s. Bild): 

1. Feldlinien (Verschiebungsdichtelinien) und Äquipotentiallinien stehen grundsätzlich 

senkrecht aufeinander. 

2. Elektrodenoberflächen sind Äquipotentiallinien. Also treten Feldlinien grundsätzlich 

im rechten Winkel aus Elektrodenoberflächen aus bzw. in sie ein. 

3. Die Potentialverteilung wird üblicherweise prozentual angegeben. Das Bezugspotential 

entspricht einem Wert von 0 %, das Hochspannungspotential 100 %. 

4. Dem Abstand a zwischen zwei Äquipotentiallinien entspricht immer die gleiche 

Potentialdifferenz ∆U = a·E. Dem Abstand b zwischen zwei Feldlinien entspricht immer 

die gleiche Ladung ∆Q = D·∆A = ε·E·∆A = ε·E·b·z auf den Elektroden (z ist darin 

die Ausdehnung der Anordnung senkrecht zur Zeichenebene). Feld- und 

Äquipotentiallinien ergeben ein Gitter von "Kästchen" mit den Seitenlängen a und b. 

Die jedem Kästchen zuzuordnende Teilkapazität ist nach den obigen Ausführungen: 

∆Q ε ⋅E⋅b⋅z b 

∆ C = = = ε ⋅z⋅ = const. 

∆U a⋅E a 

Auch das Seitenverhältnis b/a ist also konstant. Zweckmäßigerweise wählt man 

b/a = 1, also quadratische Kästchen. Dann lassen sich die Kästchen anhand der 

Bedingung konstruieren, dass ihre vier Seiten einen einbeschriebenen Kreis berühren 

müssen. 

5. Die Gesamtkapazität der Anordnung ergibt sich aus der Anzahl np der parallelen und 

der Anzahl nr der in Reihe liegenden Kästchen für den Fall b/a = 1 zu 

npnp C = ⋅∆ C = ε ⋅z⋅ n n 

r r 

Die Konstruktion des Feldbildes erfolgt, wie in dem Bild auf der nächsten Seite angedeutet, 

iterativ. Man wird in diesem Beispiel (Randfeld eines Plattenkondensators) etwa mit dem 

Zeichnen der Äquipotentiallinien 25 %, 50 % und 75 % im homogenen Bereich des Feldes 

beginnen und die Linien im Randbereich den Elektrodenkonturen folgend abbiegen. Anschließend 

werden senkrecht dazu die Feldlinien eingezeichnet, und danach erfolgt eine erste 

Kontrolle der Einhaltung der Zeichenregeln (rechte Winkel, einbeschriebene Kreise). Diese 

führt naturgemäß zunächst auf starke Abweichungen, und der Verlauf der Äquipotential- und 

Feldlinien muss nun in sich mehrmals wiederholenden Schritten solange nachgebessert 

werden, bis die Regeln mit für die jeweilige Problemstellung ausreichender Genauigkeit 

erfüllt sind. 






(nach A. Küchler: 

Hochspannungstechnik, 

VDI-Verlag 1996)


6.5 Ausnutzungsfaktoren nach Schwaiger 

Mit der analytischen Auswertung der Kontinuitätsgleichung und den Regeln zur grafischen 

Feldermittlung sind stellvertretend nur zwei der klassischen Verfahren beschrieben worden, 

elektrische Quellenfelder zu beschreiben. Andere Elektrodenanordnungen als die bisher behandelten 

erfordern andere Lösungswege. So sind viele der in der Hochspannungstechnik 

vorkommenden Anordnungen, lange bevor der Einsatz von Feldberechnungsprogrammen 

zum Standard geworden ist, analytisch untersucht worden. Dabei kamen weitere Verfahren 

zur Anwendung, wie beispielsweise die Methode der konformen Abbildung oder das Ersatzladungsverfahren, 

auf die hier nicht weiter eingegangen werden kann. Dabei erfordert es 

Übung und Erfahrung, für jede Anordnung den bestgeeigneten Lösungsweg zu finden. Es 

existiert kein einheitliches Standardverfahren, welches gleichermaßen gut auf alle Problemstellungen 

anzuwenden ist. Das trifft übrigens auch noch heute für die verschiedenen Arten 

von Feldberechnungsprogrammen zu. 

An dieser Stelle soll noch ein einfaches Hilfsmittel vorgestellt werden, mit dem ohne großen 

Rechenaufwand für eine gegebene Anordnung die höchste auftretende Feldstärke, die 

Kapazität und mit Einschränkung auch die Durchschlagspannung ermittelt werden können. In 

vielen praktischen Anwendungsfällen ist das bereits völlig ausreichend. Von Schwaiger 1 wurden 

Ausnutzungsfaktoren η eingeführt, die für eine bestimmte Anordnung das Verhältnis 

der Feldstärke E0 einer homogenen Anordnung gleicher Schlagweite (diese kann auch als 

mittlere Feldstärke der Anordnung interpretiert werden) zur tatsächlich auftretenden höchsten 

Feldstärke Emax angeben: 

E0 

U 

η = 

mit E0 

= 

E 

s 

max 

Der Kehrwert 

1 Emax 

= 

η E 

0 

ist der so genannte Inhomogenitätsgrad der Anordnung. Da die maximale Feldstärke einer 

beliebigen Anordnung nie kleiner sein kann als E0, gilt grundsätzlich 

η ≤ 1 bzw. 

1 

≥ 1 . 

η 

Der Wert von η = 1/η = 1 wird nur für eine ideale homogene Anordnung (den homogenen 

Bereich eines Plattenkondensators) erreicht. Für andere Anordnungen wird der Ausnutzungsfaktor 

als Funktion einer oder zweier als geometrische Charakteristik bezeichneten Größen 

p und q angegeben, die folgendermaßen definiert sind: 

1 A. Schwaiger, Elektrische Festigkeitslehre, Springer Verlag, Berlin, 1925 




s+ r 

p = 

r 

R 

q = 

r 

Es liegen mittlerweile teils analytisch, teils durch Näherungen gefundene Ausnutzungsfaktoren 

einer Vielzahl von Anordnungen vor, mit denen es möglich ist, die Maximalfeldstärken 

an fast jeder beliebigen Elektrodenanordnung zumindest näherungsweise abzuschätzen. 

Beispiele in Form von Wertetabellen und/oder Kurven sind auf den Seiten 30 bis 38 wiedergegeben. 

Mit Hilfe der Ausnutzungsfaktoren ist es grundsätzlich auch möglich, die Durchschlagspannung 

von Elektrodenanordnungen in Gasen abzuschätzen: 

Ûd = Êd·s·η mit Êd ... Durchbruchfeldstärke 

Das gilt jedoch nur, solange es beim Erreichen der Durchbruchfeldstärke unmittelbar zu 

einem vollkommenen Durchschlag kommt, also in homogenen bis schwach inhomogenen 

Anordnungen. Für diese liegen die Ausnutzungsfaktoren bei Werten zwischen 1 und etwa 0,3. 

Ferner ist zu beachten, dass die Durchbruchfeldstärke keine konstante Größe ist, sondern außer 

von der Luftdichte und der Art des Gases auch von der Elektrodengeometrie abgängig ist: 

Platten: 

mit s ... Schlagweite 

r ... Radius der stärker gekrümmten Elektrode 

R ... Radius der schwächer gekrümmten Elektrode 

Êd = f(s) mit s ... Schlagweite 

Zylinder ineinander, nebeneinander oder gekreuzt: 

Êd = f(r) mit r ... jeweils der kleinere der Radien 

Kugeln nebeneinander und ineinander: 

Êd = f(r) mit r .. jeweils der kleinere der Radien 

Die drei zugehörigen Abhängigkeiten sind auf Seite 39 wiedergegeben. 

Weiterhin lassen sich mit Hilfe der Lufteinheitskapazität CLE die Kapazitäten von Kugelund 

Zylinderanordnungen bestimmen: 

CKugel = εr·r·CLE mit r ... Radius der kleineren Kugel 

CZylinder = εr·l·CLE mit l ... Länge der Zylinderanordnung 

Die Lufteinheitskapazität selber ist eine Funktion der geometrischen Charakteristik p. Sie 

ist für verschiedene Kugel- und Zylinderanordnungen auf Seite 40 dargestellt. 

Für die bereits in den Abschnitten 6.3.2 und 6.3.3 analytisch hergeleiteten Verhältnisse 

an konzentrischen Kugeln und koaxialen Zylindern soll im Folgenden der Gebrauch der Ausnutzungsfaktoren 

demonstriert werden: 




Beispiel 1: Konzentrische Kugeln in Luft, r = 10 cm, R = 20 cm 

s+ r 10 + 10 

p = = = 2 

r 10 

R 20 

q= = = 2 = p 

r 10 

Aus Tabelle oder Kurve S. 30: η = 0,5 

E 

E U U 2U 

η s⋅η 0,5 ⋅( R−r) ( R−r) 0 

max = = = = 

Die gefundene Maximalfeldstärke stimmt exakt mit der analytisch berechneten Maximalfeldstärke 

(s. Seite 15) überein. 

Ermittlung der Kapazität: 

CKugel = εr·r·CLE 

Aus der Kurve S. 39, mit p = 2: CLE = 2,22 pF/cm 

CKugel = 10 cm · 2,22 pF/cm = 22,2 pF 

Vergleich mit der analytisch ermittelten Kapazität (s. Seite 15): 

r⋅R 10 cm ⋅20 

cm 

CKugel,anal. 

= 4πε0εr⋅ = 4π ⋅0,088542 pF/ cm ⋅ = 22,25 pF 

R−r 10 cm 

Beispiel 2: Koaxiale Zylinder in Luft, r = 10 cm, R = 20 cm 

s+ r 10 + 10 

p = = = 2 

r 10 

R 20 

q= = = 2 = p 

r 10 

Aus Tabelle S. 31 oder Kurve S. 32: η = 0,693 

E 

E U U U 1 U 1 

η s⋅η 0,693 ⋅( R−r) r ⎛ R ⎞ 

0,693⎜ −1) 

⎟ 

⎝ r ⎠ 

r 0,693 

0 

max = = = = ⋅ = ⋅ 

Vergleich mit der analytisch berechneten Maximalfeldstärke (s. S. 19): 

E 

max 

U U U 

= = = 

R 

r ⋅ln 

r⋅ln 2 r⋅0,693 

r 

Auch hier stimmt die mit Hilfe des Ausnutzungsfaktors gefundene exakt mit der analytisch 

berechneten Maximalfeldstärke überein. 




Die Ausnutzungsfaktoren stellen ein sehr anschauliches Hilfsmittel zum direkten Vergleich 

der Inhomogenität verschiedener Anordnungen dar. Der Vergleich von Beispiel 1 und 

Beispiel 2 zeigt unmittelbar, dass bei gleichen Radienverhältnissen die Zylinderanordnung 

einen höheren Ausnutzungsgrad aufweist als die Kugelanordnung, oder, ausgedrückt über den 

Inhomogenitätsgrad 1/η, dass die Kugelanordnung inhomogener ist als die vergleichbare 

Zylinderanordnung. Dies kann man sich damit erklären, dass die Kugelanordnung gegenüber 

der Zylinderanordnung in einer zusätzlichen Dimension (nämlich der z-Richtung) gekrümmt 

ist. 

Ermittlung der Kapazität: 

CZylinder = εr·l·CLE 

Aus der Kurve S. 39, mit p = 2: CLE = 0,775 pF/cm 

CZylinder = l · 0,775 pF/cm 

Vergleich mit der analytisch ermittelten Kapazität (s. Seite 18): 

2 ε0 r 2π 0,08542 

Zylinder,anal. 

l π ε ⋅ 

C l l 

= = ⋅ = ⋅ 0,7744 pF/ cm 

R 

ln 

0,693 

r 

Abschließend soll noch in einem weiteren Beispiel die Anwendung des Ausnutzungsfaktors 

für die Ermittlung der Durchschlagspannung einer Kugelfunkenstrecke gezeigt werden: 

Beispiel 3: Durchschlagspannung einer Kugelfunkenstrecke, r = 5 cm, s = 5 cm 

s+ r 5+ 5 

p = = = 2 

r 5 

R 5 

q = = = 1 

r 5 

Aus Tabelle oder Kurve S. 30: η = 0,732 

Aus der Kurve S. 39: Êd = 34 kV/cm 

Damit ergibt sich für die Durchschlagspannung: 

Ûd = Êd·s·η = 34 kV/cm · 5 cm · 0,732 = 124, 4 kV 

Dieser Wert weicht um nur ca. 1 % von dem in der IEC-Vorschrift 60052 angegebenen 

Wert für Messkugelfunkenstrecken ab (Ûd0 = 123 kV, vgl. Kapitel 5, S. 6). 




Ausnutzungsfaktor η von Kugelanordnungen: 

2r s 2r 

2r s 2r 

2r s 

p q = 1 q = 1 q = ∝ q = p 

1,0 1 1 1 1 

1,5 0,850 0,834 0,732 0,667 

2 

0,732 0,660 0,563 0,500 

3 0,563 0,428 0,372 0,333 

4 0,449 0,308 0,276 0,250 

5 

0,372 0,238 0,218 0,200 

6 0,318 0,193 0,178 0,167 

7 0,276 0,163 0,152 0,143 

8 

0,244 0,140 0,133 0,125 

9 0,218 0,123 0,117 0,111 

10 0,197 - 0,105 0,100 

15 0,133 - - - 



2r 

2R


Ausnutzungsfaktoren η für Zylinderanordnungen (Tabellen): 

Zylinder nebeneinander: 

2r s 2r 

p q = 1 q = 2 q = 3 q = 5 q = 10 q = 20 q = ∝ 

1 1 1 1 1 1 1 1 

1,5 0,924 0,894 0,884 0,878 0,871 0,864 0,861 

2 0,861 0,815 0,798 0,783 0,772 0,766 0,760 

3 0,760 0,702 0,679 0,658 0,641 0,632 0,623 

4 0,684 0,623 0,595 0,574 0,555 0,548 0,533 

5 0,623 0,564 0,538 0,513 0,492 0,486 0,468 

6 0,574 0,517 0,488 0,469 0,450 0,435 0,419 

8 0,497 0,447 0,420 0,401 0,377 0,368 0,349 

10 0,442 0,397 0,375 0,352 0,330 0,324 0,301 

15 0,349 0,314 0,396 0,277 0,257 0,249 0,228 

20 0,291 0,263 0,248 0,232 0,214 0,202 0,186 

50 0,1574 - - - - - 0,0932 

100 0,094 - - - - - 0,0537 

300 0,038 - - - - - 0,0214 

500 0,025 - - - - - 0,0138 

800 0,0168 - - - - - 0,00922 

1000 0,0138 - - - - - 0,0076 

Zylinder ineinander: 

2r 

2R 

2r s 2R 

2r s 

p q = p q = 3 q = 5 q = 10 q = 20 

1 1 1 1 1 1 

1,5 0,811 0,831 0,847 0,855 0,857 

2 0,693 0,717 0,735 0,748 0,754 

3 0,549 0,549 0,582 0,604 0,614 

4 0,462 - 0,478 0,507 0,521 

5 0,402 - 0,402 0,439 0,454 

6 0,358 - - 0,386 0,404 

8 0,297 - - 0,310 0,331 

10 0,256 - - 0,256 0,281 

15 0,193 - - - 0,204 

20 0,158 - - - 0,158 

50 0,0798 - - - - 

100 0,047 - - - - 

300 0,019 - - - - 

500 0,0125 - - - - 

800 0,0084 - - - - 

1000 0,0069 - - - - 



2r 

2R 

s


Ausnutzungsfaktoren η für Zylinderanordnungen (Kurven): 




Ausnutzungsfaktoren η für Spitzen-, Schneiden- und Kreisringanordnungen: 

(s. auch Seiten 34 – 38) 





Anordnungen R1, R2 (s. Seite 33) 





Anordnungen T1, T2, T3 (s. Seite 33) 





Anordnung T1 (s. Seite 33 und Seite 35) 


Anordnung K1 (s. Seite 33) 


















Durchbruchfeldstärke von Luft für Platten, Zylinder und Kugeln 

(nach: W. O. Schumann, Elektrische Durchbruchfeldstärke von Gasen, Springer Verlag, 1923) 

Durchbruchfeldstärke von Luft 

(bei Normalbedingungen: p = 1013 hPa, ϑ = 20 °C) 




Lufteinheitskapazität für Kugel- und Zylinderanordnungen 

(nach: A. Schwaiger, Elektrische Festigkeitslehre, Springer Verlag, Berlin 1925)

DA - Fachgebiet Hochspannungstechnik

Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.

Template löschen?

Als Template speichern?